產品最優求解問題中運籌學方法的應用

張青等

【關鍵詞】運籌學；最優利潤；最優產量；線性規劃；動態規劃；決策

“韓信點兵，多多益善”，“運籌”本意是算籌，后引伸為謀略，最早出于漢高祖劉邦對張良的一句評價：“運籌帷幄之中，決勝千里之外。”現代運籌學的起源可追溯到某些機構的管理中最先試用的科學手段 ，現在普遍認為，運籌學是從第二次世界上大戰初期的軍事任務開始的。所謂運籌學，是應用于數學的和形式科學的跨領域研究，利用統計學、數學模型等方法去尋找復雜問題的最佳答案。韓信點兵，并不僅僅是多多益善的問題，而更重要的卻是“運籌帷幄”問題，否則將難以發揮一個組織系統的效率和作用。運籌學作為一門新興科學，貫穿著效率和資源最優化的原則，在社會生活的廣泛領域有著實用和科學的價值。對現實中的復雜問題，都可以用運籌學的方法進行解決，并改善和優化現有系統的效率。本文意圖從運籌學在經濟管理中的廣泛運用這一方面出發，分析、論證其對經濟管理系統進行定量分析和決策，以及對經濟管理系統中人力、物力、財力等資源進行系統安排的過程，進而得出運籌學具有實現科學管理，為決策者提供最佳方案，取得最優經濟效益的實效性和科學性的結論。

1 產品最優求解問題中運籌方法運用的一般步驟

在產品最優求解問題中，經常用到的是運籌學里的兩個分支：線性規劃和動態規劃，用它們來求產品最優求解問題時的主要步驟如下：

1.1 在運用線性規劃和單純形法解決實際問題時建立數學模型一般有以下三個步驟：

（1） 提出來需要解決的問題并建立變量；

（2） 確定目標函數；

（3）分析問題所處的環境以及約束條件。

1.2 動態規劃算法的基本步驟

設計一個標準的動態規劃算法，通常可按以下幾個步驟進行：

（1）分析最優解的性質，并刻畫其結構特征。

（2）遞歸的定義最優解。

（3）以自底向上或自頂向下的記憶化方式計算出最優值。

（4）根據計算最優值時得到的信息，構造問題的最優解。

2 產品最優利潤求解問題中運籌方法的運用

應用學科的科學性體現在其具備有效的科學方法上，運籌學在經濟管理中的方法主要有線性規劃。在經濟管理中，線性規劃是目前應用最廣泛的、比較成熟的一種優化法，它經常運用在生產計劃、物資調用、資源優化配置等方面。作為生產經營管理者，常常會遇到的這類問題：一是如何有效協調、解決勞動力、資金等資源條件之間矛盾，爭取資源最大效益化；二是針對某一特定的工作目標時，如何合理組織生產，安排工藝流程，調整產品的成份，以使資源消耗最少。

例1：多品種多步驟產品最優利潤求解模型研究

某生產車間生產甲、乙兩種產品，每件產品都要經過兩道工序，即在設備A和設備B上加工，但兩種產品的單位利潤卻不相同。已知生產單位產品所需的有效時間（單位：小時）及利潤見表1。問生產甲、乙兩種產品各多少件，才能使所獲利潤最大。

分析：該問題所需確定的是甲、乙兩種產品的產量，先建立其數學模型。

設x1，x2分別表示產品甲和產品乙的產量，x1，x2稱為決策變量，根據問題所給的條件有

上述問題要確定的目標是：如何確定產量x1和x2，才能使所獲利潤為最大。利潤的獲取和x1，x2密切相關，以f表示利潤，則得到一個線性函數式

所給問題的目標是要使線性函數f取得最大值，即目標函數是

以上是決策變量x1，x2受限的條件，把它們合起來稱之為約束條件。

則本例的數學模型可歸結為：

引入松馳變量x3，x4，將問題化為標準形式：

目標函數改寫為

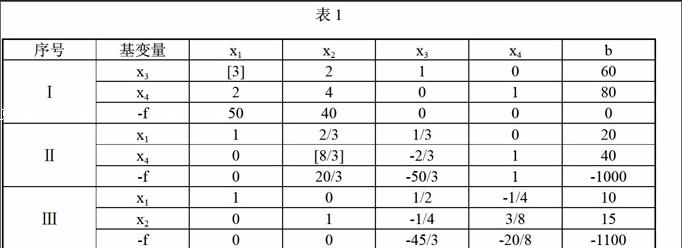
將約束條件的增廣矩陣和改寫后的目標函數的系數填入下表中，得到的表稱為單純形表：

因表1中檢驗數非正，得最優解，除去松馳變量后得；它表示：甲產品生產10件，乙產品生產15件時，最大利潤為1100元。

3 產品最優產量求解問題中運籌放得運用

事物的發展往往復雜的、多變的，線性規劃和單純形法不能解決一些復雜問題，因此動態規劃逐漸發展成為運籌學的一個分支。動態規劃算法與分治法類似，其基本思想也是將待求解問題分解成若干個子問題，先求解子問題，然后從這些子問題的解得到原問題的解。對于經濟管理中法最短路線、資源分配、設備更新、庫存管理、裝載等問題，用動態規劃方法可以很方便地求解。當然，動態規劃也不是萬能的，有它的局限性，適合用動態規劃解決問題必須滿足最優化原理和無后效性法的條件。

例2：不同產品負荷下最優產量動態規劃研究

某工廠購進1000臺機床，每臺機床都可在高、低兩種不同的負荷下進行生產，在高負荷下生產的產量函數為g（x）=10x（單位：百件），其中x為投入生產的機床數量，年完好率為；在低負荷下生產的產量函數為h（y）=6y（單位：百件），其中y為投人生產的機床數量，年完好率為b=0.9。計劃連續使用5年，試問每年如何安排機床在高、低負荷下的生產計劃，使在五年內生產的產品總產量達到最高。

分析：狀態變量sk取為第k年度度初具有的完好機床臺數。

決策變量xk為第k年度中分配在高負荷下生產的機器臺數，則為第k年度中分配在低負荷下生產的機器臺數（假定xk、sk皆為連續變量）。

狀態轉移方方程為：

第k年度的產量為：

最優值函數表示擁有機床數為sk時，從第k年度至第五年度采取最優分配方案進行生產時所獲得的最大總產量。

則動態規劃的基本方程為：

再從第5年度開始，用逆推歸納法進行計算。

計算結果表明：最優策略為

。

即頭兩年應該把年初全部機床投入低負荷生產，后三年應該把年初全部機床投入高負荷生產。這樣會使產量最高，最高產量為29139百件產品。而且，從求解的過程中反過來就能確定每年年初的狀態，即每年年初所擁有的完好機器臺數。已知s1=1000，于是可得如下結論：第一年將1000臺機器全部投入到低負荷下進行生產，第一年末機床完好數是900臺，第二年將900臺機器繼續投入到低負荷下進行生產，第二年末機床完好數是810臺，第三年將810臺機床全部投入到高負荷下進行生產，第三年末機床完好數是567臺，第四年將567臺機床全部投入到高負荷下進行生產，第四年末機床完好數是397臺，第五年將397臺機床投入到高負荷下進行生產，這樣第五年末剩下的完好機床數是278臺，五年生產產品總數為29139（百件）。

隨著科學和經濟的發展和進步，運籌學也不斷的發展完善成為近代應用數學的一個重要分支，它將生產經營中的一些難以解決的問題模型化，然后用運籌學的方法加以解決，為決策者提供定量、定性分析，幫助決策者做出最優決策。

參考文獻

[1]何堅勇編著.運籌學基礎[M].北京：清華大學出版社，2000.

[2]趙鳳至，最優化計算方法.上海：上海科學技術出版社，1983.

[3]運籌學教材編寫組.運籌學[M].北京：清華大學出版社，2005.