基于有限元法的薄壁外壓零件優化設計

周 維， 徐 鋼， 李小英

（1.中船重工電機科技股份有限公司，山西 太原 030027；2.寶雞航天動力泵業有限公司，陜西 寶雞 721001）

引言

隨著電機產品在水下領域的應用，薄壁零部件除了常規的應力外，還在水下承受外部壓力，因此必須具有足夠的強度、剛度和穩定性.使科學合理的設計該類零件尤為重要。以往大多采用經驗或類比法進行設計，不能準確計算出各部分的受力變形情況，具有很大的盲目性，為產品安全埋下了隱患。本文對某水下電機的關鍵零件進行了三維建模，利用有限元法進行了強度分析、剛度分析，同時對穩定性進行了設計，根據分析結果對零件進行了改進，收到了滿意的效果，預防了可能發生的安全隱患。

1 應力分析

根據資料可知，當圓筒的壁厚遠小于直徑時（D／δ≥20），稱之為薄壁圓筒，零件就屬于此類零件。外壓薄壁零件的失效形式主要有三種：強度不足引起的失效，將產生壓縮屈服失效；剛度不足而引起的失效，將產生過大的變形；穩定不足引起的失效（稱作失穩），突然失去零件原有形狀。

基于此，對零件不但需要進行強度分析、剛度分析，同時還應對穩定性進行分析設計。

2 三維模型建立及有限元分析

2.1 三維模型的建立及簡化

某水下電機零件二維結構圖如圖1所示，由于產品在水下運行，設計時材料選為1Cr18Ni9Ti，工作時承受2MPa外壓，變形后位移圓周方向不大于0.4mm。

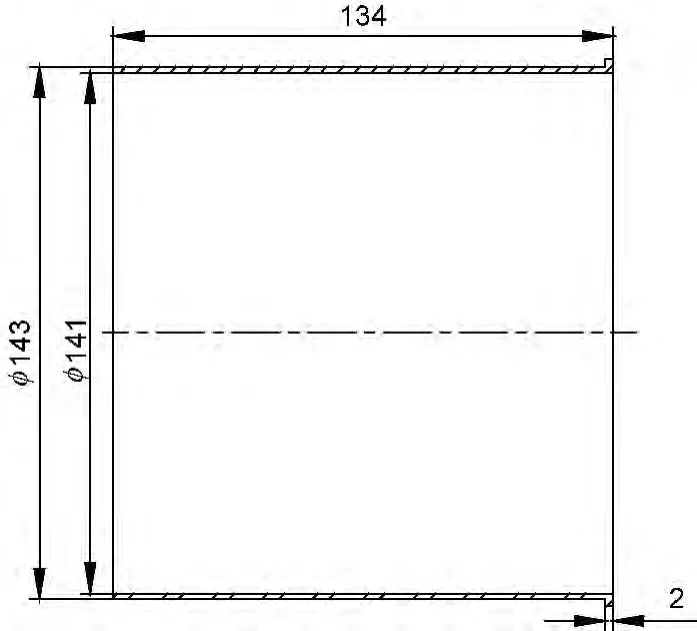
圖1 零件二維結構圖（mm）

現利用三維設計軟件對零件進行建模，在進行有限元分析時，必須對實際的結構模型進行適當的簡化，該模型的建立是為有限元分析做準備，因此忽略對分析結果影響很小的結構，以簡化分析過程，突出強度和剛度的重要性，簡化后零件三維模型如下頁圖2所示。

2.2 進行有限元分析

2.2.1 強度和剛度分析

1）傳統理論計算。

圖2 零件三維模型

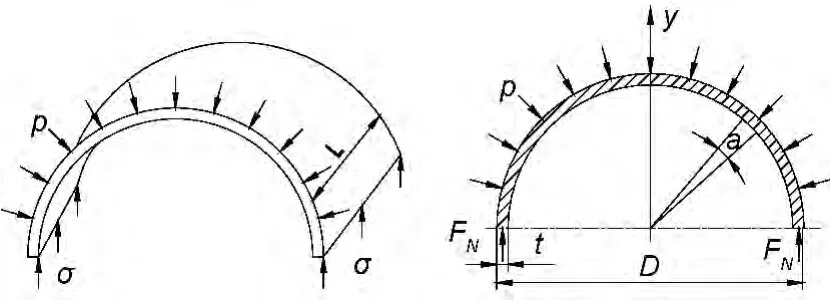
圖3 圓筒應力狀態

從圓筒中截取一部分，應力狀態如下頁圖3所示，若在筒壁的縱向截面上應力為σ，則內力為FN＝σtL，在這一部分圓筒內壁的微分面積上壓力在y方向的投影為，通過積分求出上述投影的總和為

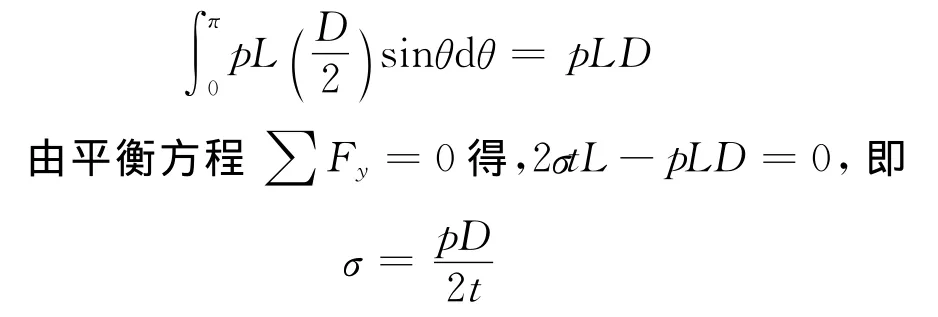
公式中：p為零件承受外壓，MPa；D為零件外直徑，mm；t為零件壁厚，mm。

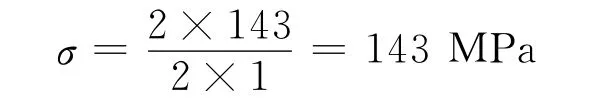
2）有限元計算。

現用有限元軟件來模擬零件承壓過程，驗證理論計算的正確性，同時為零件改進提供數據依據。零件在承壓過程時壓力是逐步緩慢加載至最大，并保持不變.因此分析類型可以確定為“靜態”。接著進行網格劃分。本文采用的解法是FFEplus算法，并采用p－自適應方法調整，將有限元分析的初始化設置完成后，運行計算，得到分析結果。為使變形結果較為清楚且又不夸張的顯示，將變形比例定為放大100倍。Simulation在管理器里生成應力分布云圖，如圖4所示，最大應力為144MPa。受載荷后應變圖如圖5所示，零件變形后最大位移位為0.33mm。

圖4 應力分布云圖

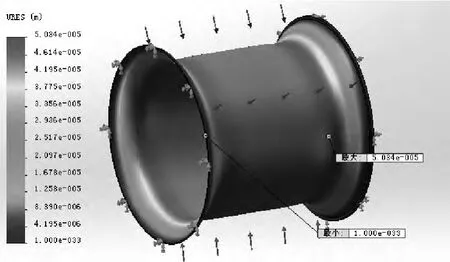
圖5 受載荷后應變圖

通過上面的有限元分析，各部位的應力都已清楚地表示，由圖4可以看出，最大應力為143.8MPa，與理論計算基本一致，證明模型的建立和約束加載正確。由圖5可以看出，最大位移為0.05mm。滿足設計要求的0.4mm。最大應力小于材料的屈服極限，安全系數n＝205／143＝1.43，可以得出設計可以滿足強度的需要。

2.2.2 穩定性分析

1）傳統理論計算。

當薄壁零件受外壓時，往往在強度很富裕的情況下，卻突然失去零件原有形狀，把這一現象稱作失穩現象。外壓零件的失穩是它的固有特性，和其它構件（例如：壓桿）失穩一樣是獨立于強度以外的問題，因此需要對薄壁零件進行另外的穩定性設計。外壓筒體失穩時，圓筒由圓形可能躍變成兩個波，三個波，四個波……n＝正整數的波形，如圖6所示。

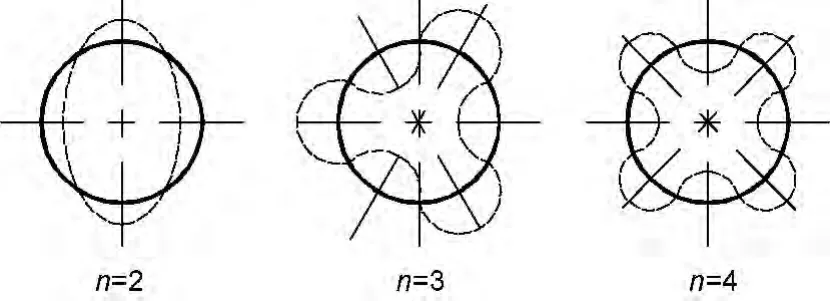
圖6 外壓圓筒失穩時的

2）判斷零件圓筒類型。

外壓零件穩定性分析時，首先需要根據計算長度的大小判定是長圓筒、短圓筒還是剛性筒。

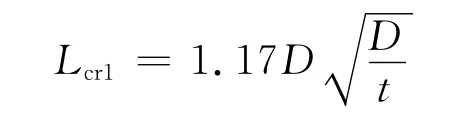
公式中：Lcr1為長圓筒與短圓筒臨界長度，mm；D為零件外直徑，mm；t為零件壁厚，mm。

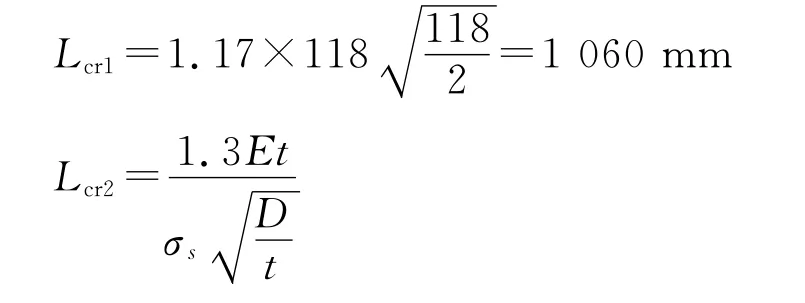
公式中：Lcr2為短圓筒與剛性筒臨界長度，mm；σs為材料的屈服強度，MPa；E為材料的彈性模量，MPa。

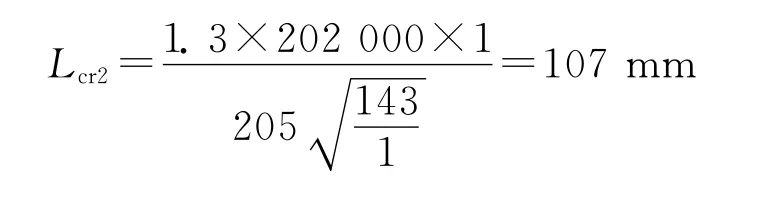
由Lcr2＜L＝134mm＜Lcr1可以判斷此圓筒為短圓筒。

3）臨界壓力計算。

短圓筒的臨界壓力可由拉默公式計算

計算許用外壓小于外壓，證明在工作中會出現不可預知的危險。

4）有限元計算。

定義屈曲模式數為2，并選擇“Direct sparse”為解算器，對第一階屈曲模式創建位移圖解，如圖7所示，可以看出薄壁圓筒由圓形躍變成六個波，這樣的變形是屈曲失效剛發生時的近似形狀。

圖7 第一階屈曲位移圖解

由圖8可以看出，屈曲的安全系數為1.12，而理論計算的安全系數n＝2.28／2＝1.14，結果也較為接近。這里需要說明的是屈曲模態表示屈曲開始時的形狀，并預測屈曲后的形狀，但不表示變形的大小。

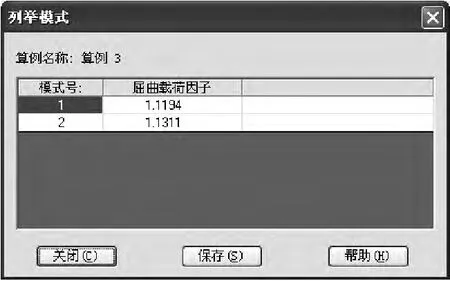
圖8 屈曲的安全系數

3 優化設計

屈曲安全系數為（1.12）小于強度安全系數（1.43），由此可見屈服是主導失效形式，因此需要增加臨界壓力。由臨界壓力公式可知，增加臨界壓力的途徑主要有：提高E值、增加壁厚t與降低L值。提高E值是指選擇高質量的高E值材質，但是鋼材的E值差別不大；增加壁厚t則增加了零件重量；降低L值受產品軸向尺寸要求制約。優化零件設計時，可以綜合幾種因素進行有限元仿真計算，得出經濟合理的方案，本文不再贅述。

4 結語

本文在進行承受外壓的薄壁圓筒設計過程中，使用了彈塑性力學理論與有限元分析相結合的方法，將薄壁圓筒的強度、剛度設計校核建立在受力分析的基礎上，同時考慮了穩定性的設計校核，可見將有限元法運用到零件的設計，可以有效的改進結構，降低了零件設計風險，從而達到了降低企業成本，節省資源的目的。可為設計該類產品開發提供借鑒。

［1］劉鴻文.材料力學［J］.高等教育出版社，2012（2）：10－12.

［2］機械設計手冊［J］.機械工業出版社，2011，5（8）：20.

［3］E·維德曼，W·克倫貝格爾.電機結構［J］.機械工業出版社，2012（2）：30.

［4］江洪等.Solidworks有限元分析實例解析［J］.機械工業出版社，2008（3）：40－42.

［5］陳超祥 葉修梓主編.SolidWorks Simulation高級教程［D］.2011版.北京：機械工業出版社.

［6］GB150－1998.鋼制壓力容器［J］.國家質量監督檢驗檢疫局，2007（6）：30.

［7］陳盛秒.薄壁外壓容器設計的公式法［J］.石油化工設備技術，2008，29（6）：15.