帶側窗動能殺傷器直接力姿態控制

韓英宏 雷延花 梁 卓 陳萬春 嚴佳民 廖選平

1.中國運載火箭技術研究院，北京100076

2. 北京航空航天大學，北京100191

目前，典型的遠程高空反TBM 導彈一般采用紅外尋的末制導［1－2］，而此類防空導彈以很高的速度飛行，氣動加熱嚴重，如果將導引頭探測窗口直接安裝在頭部，氣動光學效應將導致紅外導引頭無法正常工作。為了減小氣動加熱的影響，需要將導引頭探測窗口安裝在導彈的側面，這樣就會導致視線不對稱，需要協調導彈姿態和軌跡的控制，對控制系統的設計引入新的課題:側窗探測條件下的制導控制技術［3］。本文以帶側窗的動能殺傷器(KKV)為研究對象，設計了滿足要求的直接力姿態控制方案，為殺傷器精確制導提供了有利條件。

1 KKV 模型

1.1 帶側窗的導引頭模型

KKV 導引頭探測窗口安裝在其側面，是經過導彈頭錐其中一條母線的平面，導引頭通過側窗去發現目標，為便于描述，首先定義側窗坐標系如圖1 所示。

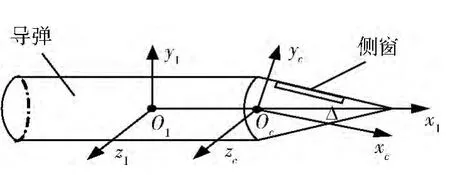
圖1 側窗坐標系示意圖

側窗坐標系原點oc取在導引頭的回轉中心，位于彈體軸上;ocxc軸在彈體縱對稱平面內，平行于側窗表面，指向彈體頭部為正;ocyc在彈體縱對稱平面內，垂直于ocxc軸，指向上為正;oczc垂直于縱對稱平面ocxcyczc，方向按右手定則確定。

由定義可知，彈體系與側窗系均與彈體固連，為動坐標系，且2 者的方位只需用一個角度Δ(該角度值為KKV 的半頭錐角，本文取為15°)即可確定，ocxc在o1x1下方Δ 為正值。假設目標在側窗系中的坐標為，則其在彈體系中的投影為:

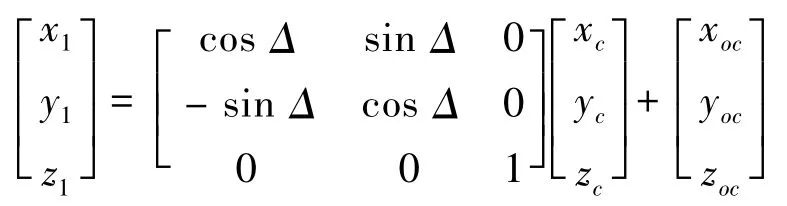
對于視場的約束，應該體現在側窗系下的視線角。本文的視線角約束為:qβc∈(－5°，5°)，qεc∈(25°，75°)，其中qβc和qεc分別為側窗系下的視線方位角與視線高低角，計算公式如下:

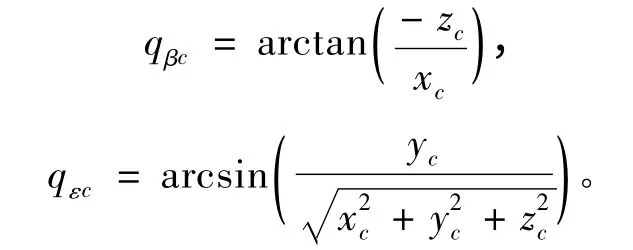
1.2 直接力姿控發動機模型

本文研究的KKV 有6個姿控發動機安裝在攔截器的尾部，其布局如圖2 所示。

控制俯仰運動時需要1，3 或2，4 工作，控制偏航運動時需要5 或6 工作，控制滾轉運動時需要2，3 或1，4 工作。

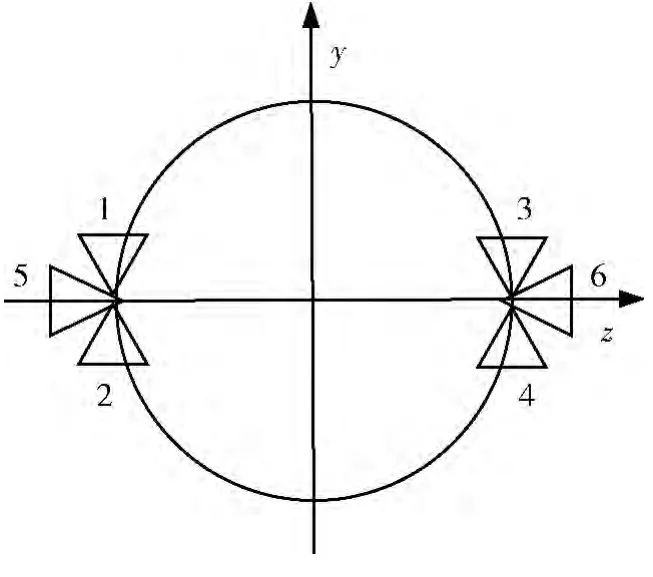
圖2 姿控發動機安裝示意圖

由于姿控發動機的推力比較小，在接收到開機指令后能瞬間達到穩定值，因此忽略推力上升時間，將其看作常值。姿控發動機工作時產生的作用力矩分別是:

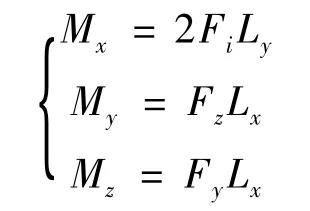
式中，Mx，My，Mz依次表示姿控發動機在彈體坐標系的作用力矩;Ly表示發動機1 ～4 推力作用點到彈體軸線的距離;Lx表示姿控發動機推力作用點到KKV 質心的距離;Fy，Fz表示相應工作狀態下俯仰和偏航方向的作用力;Fi為滾動控制時發動機的推力大小。

2 姿控方案設計

2.1 滾動通道控制方案設計

當導引頭開始工作時，目標很可能沒有在視場范圍內，需要KKV 調整姿態去捕獲目標。由于滾轉和俯仰通道共用4個姿控發動機，若2個通道均需要控制，則要考慮通道控制的優先級問題［4］。為減弱各通道之間的相互影響，本文優先控制滾轉通道，當滾轉通道無需再控制的情況下再進行其它通道控制。

KKV 滾動通道的轉動動力學方程如下:

式中，Jx1，Jy1，Jz1為KKV 的轉動慣量，在對稱外形下，Jy1= Jz1;Mzx，Mgx為姿控發動機產生的滾動力矩，Mqx為氣動力矩。姿控發動機推力恒定不變，在高空忽略空氣動力的條件下，角速度變化的斜率應該保持不變。

假設中末制導交班時刻滾轉角速度為0，期望系統按照圖3 ～5 所示的理想情況進行控制。本文的滾動控制策略以側窗系下視線方位角為依據，其最佳值為0° 。當達到最佳視線方位角時，理想的滾動角速度應該為0，使視線穩定在該位置。在目標剛好進入到導引頭側窗視場的時刻，即tc－Δt 時，控制力矩換向。為保證滾轉角速度穩定時為0，加速滾動時間應與減速滾動時間相等，均為Δt，且其最大值Δtm應滿足:

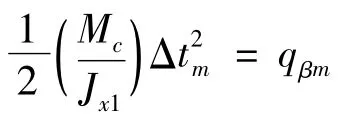
式中，qβm為側窗系下視線方位角的邊界值。

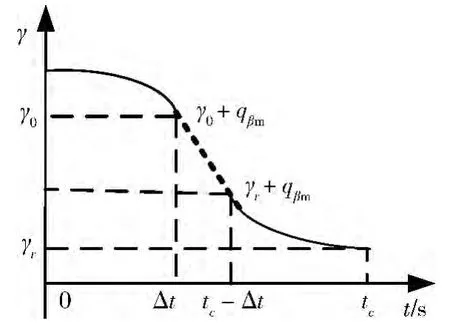
圖3 滾轉角變化曲線

圖4 滾轉力矩

根據上面的分析，設計如圖6 所示的控制流程。

在捕獲到目標之后，該控制方案同時可以保證導引頭能很好地跟蹤目標。

2.2 俯仰和偏航通道控制方案設計

俯仰和偏航通道控制可以采用滑模控制［5］，以俯仰通道為例，選取滑動模態:

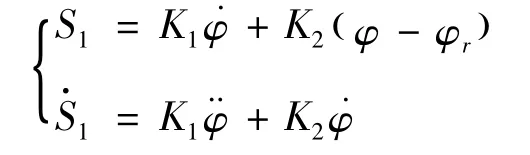
式中，φ 為KKV 的俯仰角，φr為其跟蹤指令，控制量為姿控發動機的開、關機信號指令。這里跟蹤指令選為地面系的視線高低角，但由于側窗結構的存在，還要減去KKV 的半頭錐角。若有最佳視線角要求，則可以跟蹤常值視線角。

1)S1≥Δ1，發動機2，4 開，1，3 關;

2)S1≤－ Δ1，發動機2，4 關，1，3 開;

比例系數K1，K2的選取對控制精度和跟蹤速度都有影響，因此其大小選擇至關重要。一般情況下，可以依托具體的模型，通過大量仿真來逐步篩選出合理的數值。

偏航通道用5，6 兩個發動機進行控制，方案與俯仰通道類似，其滑動模態選擇如下:

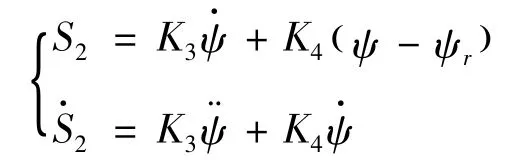
式中，ψ 為KKV 的偏航角，ψr為其跟蹤指令，這里選為地面系下的視線方位角。對于2個比例系數和開機閾值的影響，分析方法與俯仰通道相同。

3 仿真分析

根據上面提供的方案，進行大氣層外KKV 姿態控制仿真研究。采取準滑模控制時，俯仰和偏航通道控制器的相關參數設置如表1 所示。仿真結果如圖7 ～10 所示。

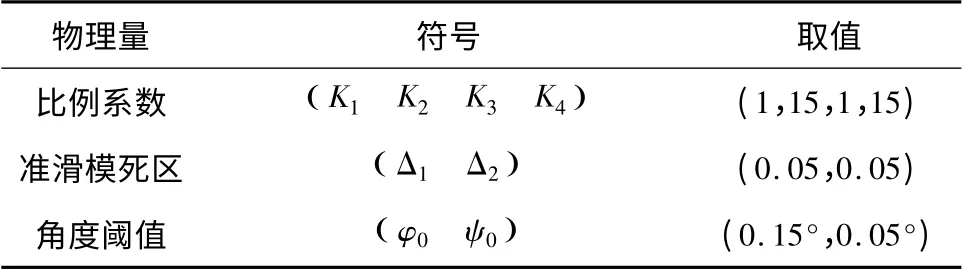
表1 KKV 姿控準滑模控制仿真參數

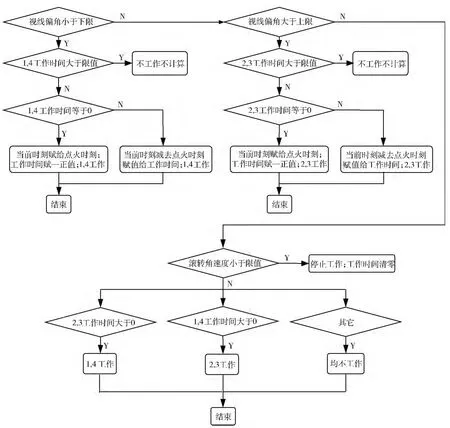
圖6 滾動通道控制流程圖

從圖7 可見，根據視線方位角對滾動通道進行控制，有效保證了視線方位角回歸到視場內，圖8 中俯仰和偏航2個通道的角度跟蹤誤差均趨近于0，3個通道的控制策略，使側窗系下的視線高低角和視線方位角都在規定的范圍之內，表明導引頭能很好地捕獲和跟蹤目標，如圖9 所示。圖10 為3個通道的發動機工作情況，可以看到，為了在穩定跟蹤目標前提下能夠最大效率地減小視線角速度，在目標進入導引頭視場之后進行的俯仰和偏航控制，使這2個通道的發動機開關頻率較高，且由于控制抖動，使目標經常到達視場邊界，需要進行滾動控制使其回到視場中心。

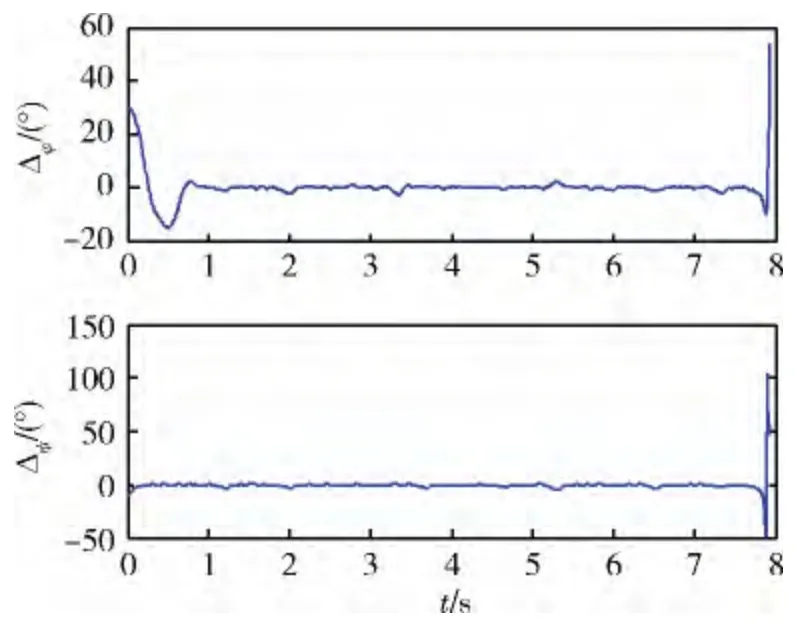
圖8 俯仰和偏航通道跟蹤誤差

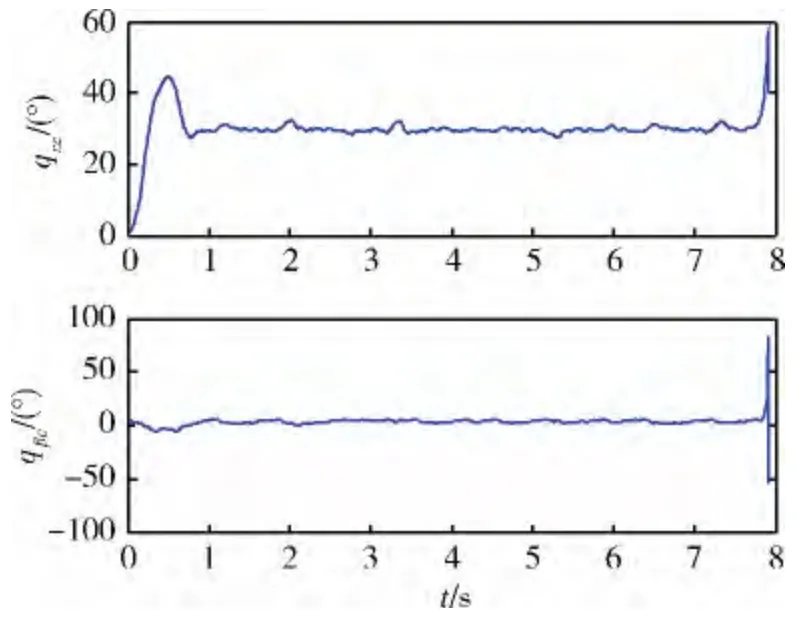
圖9 側窗系下視場角變化曲線

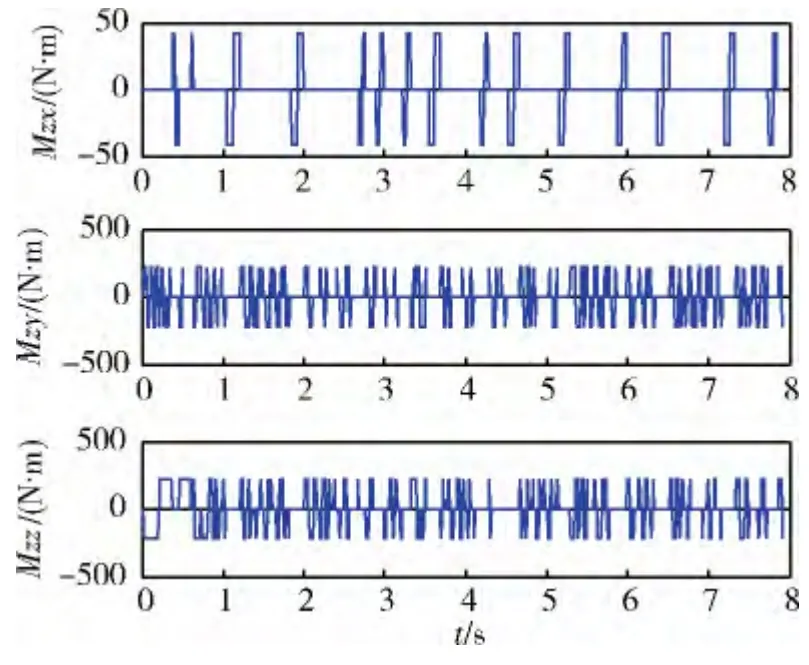
圖10 姿控發動機工作情況

4 結論

給出了KKV 控制的姿控發動機模型，針對帶側窗的導引頭，定義了側窗坐標系，計算出側窗系下的視線高低角和視線方位角，并根據這2個角度的視場約束，設計了高空滾動控制策略，用準滑模控制方法設計了俯仰和偏航通道的控制方案。仿真結果表明，本文設計的直接力姿態控制方案簡單易行，對帶側窗導引頭的飛行器姿態控制有較強的適應性，具有一定的工程應用前景。

［1］王戌瑞. 攔截彈中的紅外技術［J］. 激光與紅外，1999，29(1):3-8.(Wang Xurui.The infrared technology for the interceptor［J］. Laser and Infrared，1999，29(1):3-8.)

［2］范晉祥.美國動能攔截彈紅外成像導引頭的發展分析［J］. 紅外與激光工程，2009，38 (1):1-6. (Fan Jinxiang. Development analysis of infrared imaging seekers of kinetic kill vehicles in america［J］. Infrared and Laser Engineer，2009，38 (1):1-6.)

［3］支強，蔡遠利.動能殺傷器側窗定向機制分析及建模［J］.西安交通大學學報，2012，46(1):91-97. (Zhi Qiang，Cai Yuanli. On side window orientation of kinetic kill vehicle［J］. Journal of Xi’an Jiaotong University，2012，46 (1):91-97.)

［4］B J Strauss，R J Gravina，C J Hasenzahl，et al. All Attitude guidance and control for endoatmospheric intercepts［C］. AIAA SDIO Annual Interceptor Technology Conference，1993，AIAA 93-2643.

［5］Yeh F. K，Chien H. H，Fu L. C，Nonlinear optimal sliding mode midcourse controller with thrust vector control［C］. Proceedings of the American Control Conferrence，2002，1:348-353.

［6］宋明軍，魏明英.側窗探測條件下的制導控制系統設計方法研究［J］. 現代防御技術，2007，35(5):71-75.(Song Mingjun，Wei Mingying. Control and guide system design method for side window detection［J］.Modern Defence Technology，2007，35(5):71-75.)

［7］楊寶慶，姚郁，賀風華. 大氣層外攔截器開關式姿態控制律設計［J］. 哈爾濱工業大學學報，2010，42(1):5-8.(Yang Baoqing，Yao Yu，He Fenghua. Design of on-off Attitude Control Law Based on Model Predictive Control［J］. Journal of Harbin Institute of Technology，2010，42 (1):5-8.)

［8］章虹虹，姜杰.準滑模控制在大氣層外攔截器姿態控制中的應用［J］. 航天控制，2007，25 (5):39-42.(Zhang Honghong，Jiang Jie. The application of pseudsliding mode control in attitude control for EKV［J］.Aerospace Control，2007，25 (5):39-42.)