基于Granger 方法和ECM 模型的制造業與物流業聯動發展研究——以合肥市為例

梁 雯，秦勝杰

（安徽大學 商學院，安徽 合肥 230601）

LIANG Wen,QIN Sheng-jie

(School of Business,Anhui University,Hefei 230601,China)

在全球供應鏈和國際競爭形勢不斷嚴峻的背景下，制造業物流的發展可以加快中國制造業現代化發展的步伐，提高中國制造業企業在國際市場中的優勢地位。兩業聯動發展成為國家關注的重點問題，2007年，國家發改委在上海召開首屆全國制造業與物流業聯動發展大會之后，兩業聯動得到了社會各界的廣泛關注，業內各界則開始積極地探索兩者聯動發展。2009年，國務院發布《物流業調整和振興計劃》，文件中明確地將制造業與物流業聯動發展作為重點工程之一，2010年，全國現代物流工作部際聯席會議辦公室公布了《關于促進制造業與物流業聯動發展的意見》，指出各級政府應當參考《意見》根據本地實際情況制定出促進當地兩業聯動發展的政策法規。這些綱領性文件的實施均凸顯出國家對兩業聯動發展的密切關注。實際上，依據中國物流與采購聯合會數據顯示，2012年中國工業品物流總額占中國社會物流總額比重已達到91.4%。因此，關于兩業的互動結合、聯動發展需要穩步推動。

在地區發展上，近年來合肥市緊緊依托作為綜合交通樞紐城市、承接產業轉移示范區的核心城市等政策賦予的發展優勢，大力支持國內外汽車、裝備制造、電子信息、化工、家電、農產品加工等產業的發展。目前制造業總體上已初具規模，合肥市逐漸地向成為全國性先進制造業基地這一目標邁進。2013年，合肥市實現規模以上工業增加值1 907.40億元，比上年增長14.4%。工業增加值占GDP 比重由上年的43.6%提高到43.9%。盡管物流業發展速度較快，在地區生產總值上所占比重仍然不高，與沿海發達城市相比較，制造業與物流業發展水平仍不具有明顯優勢。面對經濟發展新常態，合肥市應積極運用新舉措，實現新發展。及時地依托兩業聯動對經濟的推動以達到在未來激烈的區域發展競爭中取得優勢地位。因此，兩業融合發展已刻不容緩。這將會加速本地區制造業產業結構轉型升級的速度以及促進當地的經濟發展。

1 文獻綜述

近年來關于兩業聯動中的問題日益成為業內學者的研究重點，相關研究從不同角度出發進行探討，何明珂指出制造業物流發展將會對國民經濟有顯著影響，制造業物流支撐著中國物流的發展[1]。王佐則認為兩業聯動的機理是以何種方式配置制造業企業資源，以及對物流管理自營與外包的交易成本比較[2]。基于博弈論的視角，王曉艷定性論證制造業與物流業選擇聯動具有長期顯著作用[3]。吳群（2011）從共生模式的角度出發將制造業與物流業的關系分為五類：平等共生型、依托共生型、嵌入共生型、互補共生型以及輔助共生型[4]。王珍珍通過對現有研究的分析，指出未來的研究可將制造業與物流業聯動作為一個研究主體與產業轉移、產業結構轉移等結合起來探討[5]。一些學者則依據具體數據構建模型以探析兩業聯動關系，韋琦運用協整檢驗對中國1998～2008年的制造業與物流業統計數據進行實證分析，得出中國制造業與物流業存在長期均衡關系且物流業增長是制造業發展的Granger 的原因[6]。劉丹運用灰色關聯模型對福建省制造業和物流業的關聯度和協調度進行實證研究，指出制造業和物流業緊密相關[7]。王軍、曹麗新運用DEA 方法對青島市2001～2011年的相關數據進行分析，論證了青島市兩業聯動水平并不高[8]。

分析各類關于制造業與物流業聯動發展的文獻，往日學者們關注的重點主要聚焦在國家、省層面的制造業與物流業聯動發展，而具體到市層面上的兩業聯動探索則相對較少；對合肥市的研究上，一部分學者則定性分析了兩業聯動發展關系，缺乏依據具體數據進行實證分析的定量描述，基于此本文通過構建ECM 模型與Granger 因果關系檢驗對合肥市2004～2013年的統計數據進行實證分析，從而為提出關于兩業聯動的建議奠定實證基礎。

2 實證分析

本文通過運用協整分析對合肥市制造業與物流業的關系進行分析，以期為合肥市未來兩業的深化發展提供思路與建議。

2.1 指標選擇與數據選取

在選擇指標時，考慮到數據的精確性、可靠性與可獲得性，選取制造業增加值與物流業增加值作為研究兩個產業發展的總量指標，從而作為實證分析的基礎。而在宏觀經濟中，目前并沒有單獨核算物流業數據的指標存在，因此，參考陳赤平學者[9]的研究，利用交通運輸業、倉儲與郵政業（不含電信業）增加值數據代表物流業的發展數據。由于現實條件的限制，個別年份的合肥市制造業數據難以有效衡量，而制造業在工業中占重要比重，可以達到90%以上。因此，為保證數據的可獲取性，本文將采用工業增加值指標代表制造業的發展層次。其中工業增加值與交通運輸業、倉儲與郵政業（不含電信業）增加值分別用Ma 與Log 表示。為保證數據精確度，并降低異方差以及多重共線性的影響，本文對工業增加值與交通運輸業、倉儲與郵政業（不含電信業）增加值均取自然對數，并分別用lnMa 與lnLog 表示。本文中數據均來自于歷年《合肥市統計年鑒》[10]。

根據以上選定的指標，從《合肥市統計年鑒》中選擇出2004～2013年度相關的原始統計數據，并以表格形式列出，如表1所示。

為避免數據的劇烈變動，對表1 中的原始數據均作自然對數變換，并以此新數據運用Eviews 7.0 軟件做時間趨勢圖形，如圖1 所示。

通過分析圖1，可以看出在2004～2013年期間合肥市制造業與物流業增長和變化趨勢大體上相似，且隨著時間的不斷變化，制造業與物流業均呈現出上升趨勢。因此，可以直觀地判斷兩業之間可能存在一定的相關性關系。

2.2 協整分析

本文引入Engle 和Granger 在1987年提出的兩步檢驗法，即EG 檢驗法，分析合肥市制造業與物流業之間是否存在長期的協整關系。而協整檢驗的首要條件是時間序列須為同階單整序列，因而需要確定序列lnMa 與lnLog 是否單整。

2.2.1 平穩性檢驗。根據協整理論，可以知道當兩個時間序列是同階單整時，表明序列可能具有協整關系。然而，經研究發現，在一般情形下經濟時間序列并不是平穩的，大多數會隨著時間的變動而發生改變。因此，為預防“偽回歸”現象的出現，有必要采用ADF 檢驗方法對時間序列做單位根檢驗，以判斷是否符合協整分析的條件。結果如表2 所示。

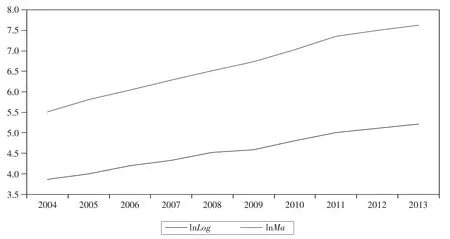
圖1 合肥市制造業與物流業的時間趨勢分析

表2 變量的單位根檢驗情況

由表2 中可以發現，lnMa 與lnLog 的原序列含有單位根，表明序列lnMa 與lnLog 處于不平穩的狀態。而對lnMa 與lnLog 的原序列做一階差分處理后，結果表明其一階差分序列均不含有單位根，并且都在10%的顯著性水平下通過檢驗，即lnMa 與lnLog 是一階單整序列。因此，可以認為變量lnMa 與lnLog 符合進行協整檢驗的首要條件。

2.2.2 協整檢驗。對變量lnMa 與lnLog 進行ADF 檢驗之后，結果表明兩變量具備進行EG 兩步檢驗法的條件。為檢驗兩變量是否協整，設兩個變量lnLog 與lnMa 之間存在線性回歸模型，即如下所示：

其中：α 代表的是合肥市交通運輸業、倉儲郵政業（不含電信業）自發增加值，β 代表的是合肥市制造業增加值每變動1個百分比時，合肥市物流業將會變化的百分比。

因此，以lnLog 為因變量，lnMa 作為自變量，本文通過運用Eviews7.0 軟件對變量lnMa 與lnLog 進行普通最小二乘回歸得到回歸方程關系式，結果如下：

R-squared=0.9973,Adjusted R-squared=0.9969，D.W.=3.075（其中***、**、*分別表示系數在1%、5%、10%的置信水平下顯著）。

上述式（2）表明，兩者之間存在明顯的正相關關系，當lnMa 每增加1 個百分比時，變量lnLog 變動0.6356 個百分比。即合肥市制造業增加值每提高1%時，合肥市物流業增加值提升0.6356%。

從式（2）得到模型估計殘差u贊=lnLog-0.3415-0.6356lnMa，為檢驗上述模型估計殘差序列的平穩性，重新定義殘差序列為ECM，并對序列ECM 進行ADF 檢驗以確定其是否存在單位根，ADF 檢驗結果見表3。

表3 殘差序列ECM 的ADF 檢驗結果

由于殘差序列ECM 的ADF 檢驗值是-6.1364，小于1%水平下的臨界值-5.5219。因此，可以認為殘差序列ECM 表現出平穩的狀態，即序列ECM 為零階單整序列，序列lnMa 與序列lnLog 之間存在協整關系，進而得出序列lnMa 與序列lnLog 之間具有長期穩定的均衡關系。

2.3 誤差修正模型（ECM）

由EG 兩步協整檢驗的結果表明合肥市制造業與物流業之間具有長期穩定的均衡關系，然而協整檢驗并未涉及到短期波動中的情況。因此，本文采用由Davidson，Hendry，Srba 和Yeo 于1978年提出的誤差修正模型（ECM）進行研究短期波動時兩業的關系[11]。

由式（2）可知，序列lnMa 與序列lnLog 之間的協整回歸方程為：lnLog=0.3415+0.6356lnMa，然后將協整方程的殘差項序列作為誤差修正項，從而構建誤差修正模型（ECM）如下：

通過運用Eviews7.0 軟件，在協整回歸方程的基礎上，對式（3）進行估計，建立誤差修正模型：

R-squared=0.9276，Adjusted R-squared=0.9035，D.W.=2.3474（其中***、**、*分別表示系數在1%、5%、10%的置信水平下顯著）。

由式（4）中可以看出，誤差修正模型的可決系數為0.9279，調整后的可決系數可以達到0.9035，表明所建模型的擬合優度較好，從而比較好地反映了變量lnMa 與lnLog 在短期波動中的影響。其中ΔlnMa 的系數在1%的顯著性水平下時通過且為正值，表明在短期波動中，lnMa 的增長率對lnLog 的增長率是正向影響。當前一期的lnMa 增長率提升1%時，lnLog 的增長率提高0.5085%。而誤差修正項ECM 的系數則表明了工業增加值與物流業增加值在短期波動時其偏離長期均衡關系的程度，因此，當短期出現變化而偏離長期均衡時，將會以-1.6926 的反向調整力度將兩者由非均衡狀態拉回均衡狀態。

2.4 格蘭杰（Granger）因果關系檢驗

通過協整分析發現合肥市制造業與物流業具有長期穩定的均衡關系，然而合肥市兩業之間的因果關系是否存在以及表現出何種的關系，仍需通過Granger 因果關系檢驗作進一步實證研究。而Granger 檢驗是建立在VAR 模型之上的，因此，需要構建VAR 模型并確定最大滯后階數。由于序列lnMa 與序列lnLog 均是一階單整序列，因此，我們可以構建VAR 模型，且根據AIC 與SC 最小原則，經過多次嘗試，最終認為最大滯后階數為1 時VAR 模型滿足穩定性條件，AR 根均處于單位圓之中。檢驗結果如圖2 所示。

滯后階數的選取對Granger 因果關系檢驗的結論具有顯著的影響，因而依據構建的VAR 模型我們采用滯后期為1 對兩者進行Granger 檢驗，結果如表4 所示。

圖2 AR 根圖

表4 格蘭杰（Granger）因果關系檢驗

由Granger 因果關系檢驗發現在顯著性水平為1%時，合肥市工業增加值是物流業增加值的Granger 原因，而合肥市物流業增加值不是工業增加值的Granger 原因，兩者之間僅存有單一方向的Granger 因果關系。這一結果表明合肥市制造業對物流業的增長具有顯著的推動作用，而物流業對制造業的發展提升相對不足，合肥市兩業聯動的發展層次還具有進一步提升的空間。而導致合肥市物流業未能有效拉動制造業的原因可能是合肥市部分物流企業規模相對較小，自身的專業化實力較弱，服務水平和品質不高，物流企業對于現代生產所要求的一體化物流服務能力發展不足，難以滿足制造業企業的物流需求。

3 結論與建議

本文以工業增加值作為體現制造業發展層次的指標，以交通運輸、倉儲與郵政業（不含電信業務）增加值數據代表物流業的發展數據，運用2004～2013年的相關統計數據對合肥市兩業聯動水平進行實證研究，得到以下結論：

（1）協整分析表明盡管工業增加值與物流業增加值的原序列表現為不平穩的狀態，然而合肥市兩業之間具有長期穩定的均衡關系。

（2）從誤差修正模型（ECM）的估計結果來看，當合肥市兩業在短期波動中偏離長期均衡時，將會以-1.6926 的反向調整方式將兩者拉回到均衡狀態。Granger 因果檢驗則表明合肥市兩業之間僅具有單一方向的Granger 因果關系，合肥市制造業對物流業的推動作用明顯，而物流業對制造業的提升相對不足。

因此，依據以上結論給出了推動兩業聯動發展的對策。對物流企業來說，要盡快適應本地制造企業對物流服務的要求，通過開展與知名物流企業的交流合作，著力提升自身的服務水平；與制造業企業在物流標準、物流業務流程、信息共享方面上開展創新性合作，提高其面向制造業企業的供應鏈管理能力，切實達到制造企業對物流成本控制的要求，促使制造業不斷提出新的物流需求，深化兩業的聯動發展層次。鼓勵制造企業適時轉變物流觀念，將非核心的物流服務交給有專業實力的物流公司運營，做大物流市場，提升制造業對物流產業的拉動作用。政府應該從促進兩業聯動的政策上給予更多扶持，優化兩業聯動的外部環境，調整制造企業物流外包的稅收政策；開展物流業與制造業聯動的示范工程，以起到良好的導向作用，引導本地制造業與物流業的聯動發展。

[1]何明珂.制造業物流發展的新需求[J].中國物流與采購，2008(5):32-34.

[2]王佐.制造業與物流業聯動發展的本源和創新[J].中國流通經濟，2009(2):16-19.

[3]王曉艷，李道芳.安徽省制造業與物流業聯動發展研究[J].華東經濟管理，2009(10):158-160.

[4]吳群.制造業與物流業聯動共生模式及相關對策研究[J].經濟問題探索，2011(1):72-75.

[5]王珍珍.制造業與物流業聯動發展綜述[J].管理學刊，2014(1):41-47,57.

[6]韋琦.制造業與物流業聯動關系演化與實證分析[J].中南財經政法大學學報，2011(1):115-119.

[7]劉丹.制造業與物流業協調發展的實證研究[J].福州大學學報（哲學社會科學版），2012(3):27-30.

[8]王軍，曹麗新.基于DEA 分析的制造業與物流業聯動發展協調度提升研究——以青島市為例[J].前沿，2012(22):90-92.

[9]陳赤平，楊茂富，楊歡.制造業與物流業聯動發展關系研究——以湖南省為例[J].湖南社會科學，2014(4):125-128.

[10]合肥市統計局，國家統計局合肥調查隊.2014 合肥統計年鑒[M].北京：中國統計出版社，2014.

[11]易丹輝.數據分析與E-views 應用[M].北京：中國人民大學出版社，2008.