基于PAM和簇閾值的改進K-Means聚類算法

卜旭松，劉立波，石　磊

(1.寧夏大學 數學與計算機學院，寧夏 銀川 750021;2. 湖北工程學院 現代教育技術中心，湖北 孝感 432000)

基于PAM和簇閾值的改進K-Means聚類算法

卜旭松1，劉立波1，石磊2

(1.寧夏大學 數學與計算機學院，寧夏 銀川 750021;2. 湖北工程學院 現代教育技術中心，湖北 孝感 432000)

摘要:為了彌補K-Means算法對孤立點數據敏感的缺陷，提高K-Means算法對包含孤立點數據集的聚類效果，在深入研究K-Means算法的基礎上，提出了基于PAM和簇閾值的改進K-Means聚類算法。該算法首先對待聚類數據進行抽樣，然后利用PAM算法獲取樣本數據的聚類中心，以樣本數據的聚類中心作為K-Means算法的初始聚類中心。在聚類迭代過程中動態計算各簇閾值，利用簇閾值準確地過濾孤立點數據。實驗結果表明，本文提出的算法不僅聚類時間短，而且具有較高的聚類準確率。

關鍵詞：采樣；K-Means聚類；聚類閾值；孤立點

中圖分類號：TP18

文獻標志碼：碼：A

文章編號：號：2095-4824(2015)03-0036-04

收稿日期：2015-03-03

作者簡介：卜旭松(1988-)，男，山東煙臺人，寧夏大學數學與計算機學院碩士研究生。

Abstract：In order to overcome the weakness of K-Means algorithm which is sensitive to outliers, and to improve the quality of K-Means clustering algorithm, the paper makes an in-depth study on the traditional K-Means algorithm and proposes an improved clustering algorithm based on the PAM algorithm and the cluster threshold. The proposed method first samples the clustering data and then employs the PAM algorithm to obtain the clustering center of the sample data as the initial center of K-Means algorithm. By calculating the threshold for each cluster dynamically in the iterative process of clustering, the outliers can be excluded from the dataset. Experimental results indicate that the proposed algorithm have been shown lower computational cost and higher clustering accuracy.

劉立波(1974-)，女，寧夏銀川人，寧夏大學數學與計算機學院教授，博士后。

石磊(1986-)，男，內蒙古興安盟人，湖北工程學院現代教育中心實驗師，碩士。

聚類是一種無監督的分類方法[1]。作為一種有效的數據挖掘技術，聚類分析可以發現數據的分布，觀察每個簇的特征，便于將進一步分析集中在某個特定的集合上。目前，聚類分析已經廣泛地應用于商務智能、圖像模式識別、Web搜索[2]、市場營銷、生物學[3]和安全等領域。

K-Means算法是一種基于劃分的聚類方法，算法以簇內點的均值作為簇的聚類中心[4-7]。孤立點是顯著偏離數據集中其他數據的點，不屬于任何簇[8]。孤立點的存在，嚴重影響了簇均值，致使簇的聚類中心顯著偏離數據的實際中心，影響了其他對象到簇的分配，導致算法準確率降低。基于密度[9-10]、區域劃分[11]等初始聚類中心的優化算法盡管能為算法提供優質的初始聚類中心，但無法處理后繼迭代過程中孤立點對簇中心重新計算引起的誤差，最終影響聚類的準確性。文獻[12]采用鄰域密度方法對數據進行預處理，把指定鄰域內包含其他對象數量少于Minpts的對象作為孤立點過濾掉。由于處理后的數據集不含孤立點數據，因此算法聚類準確率較高，但單獨處理孤立點會增加算法的時間開銷，嚴重影響算法整體執行效率。

本文從初始聚類中心選取和聚類規則兩方面對傳統K-Means算法進行改進。利用PAM算法獲取樣本數據的聚類中心作為K-Means算法初始聚類中心，利用閾值系數與簇邊距乘積作為簇閾值。在聚類過程中同步過濾孤立點數據，避免單獨處理孤立點數據增加額外的時間開銷，使算法具有較高準確率的同時保持較高的執行效率。

1　相關理論及定義

1.1　相關定義

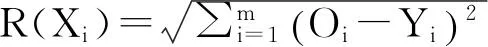
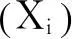
離簇Ci距離最近的簇Cj的質心。

定義3對于一個簇u，如果樣本數據集s大小滿足：

本文假設各簇數據量為uavg=N/K，N為數據集數據總量，則樣本數據量Savg為：

1.2　PAM算法

PAM算法是一種基于代表對象的技術，算法不采用簇均值作為聚類中心，而是選擇簇中實際對象作為聚類中心，因而不易受孤立點影響，對小規模數據集合非常有效，但缺點是算法時間復雜度高，當數據量較大時算法執行效率不高。研究表明，在樣本數據合適、取樣均勻的情況下，抽樣數據可以較為真實地反映總體數據集的分布狀況[14]。本文利用PAM算法對樣本數據進行聚類，獲取樣本數據的聚類中心作為K-Means算法的初始聚類中心，以樣本數據的簇邊距作為K-Means算法初次迭代的簇閾值計算參數。PAM算法描述如下：

輸入：結果簇的個數k；D：包含n個對象的數據集合。

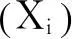
步驟：

(1) 從D中隨機選取k個對象作為初始的代表對象或種子；

(2)repeat；

(3) 將每個剩余的對象分配到最近的代表對象所代表的簇；

(4) 隨機地選擇一個非代表對象Orandom；

(5) 計算用Orandom代表對象的總代價S；

(6)ifS<0，then用Orandom替換Oj，形成k個新的代表對象集合；

(7) until聚類中心和簇邊距不再發生變化。

1.3　簇閾值設置

傳統的K-Means算法無法處理孤立點，對包含孤立點的數據集聚類準確率低。本文對K-Means算法的聚類準則進行改進，通過設置閾值方式過濾孤立點，算法以閾值系數ε和各簇的簇邊距乘積作為各簇簇閾值。與全局閾值相比，局部簇閾值更能準確地反映各簇的區域范圍，具有過濾孤立點數據的能力。由于K-Means算法初次迭代過程中無簇邊距信息，利用PAM算法獲取樣本數據的簇邊距與閾值系數ε乘積作為簇閾值，在后繼迭代過程中使用上次迭代分配到該簇的對象重新計算簇邊距并更新簇閾值，使簇閾值更加準確。使用簇閾值過濾孤立點的步驟如下:

(3) 若不滿足步驟(2)，則將點X劃分到孤立點集中。

2　改進的K-Means算法

算法基本思想如下：依據定義3進行抽樣，利用PAM算法獲取樣本數據的k個聚類中心。對于數據集中每個對象，計算其到各個簇中心的歐式距離dx，若該對象與某簇最相似且dx不大于該簇的簇閾值，則將該對象劃分到該簇，否則將該數據對象劃分到孤立點數據集。重新計算簇均值和簇閾值，重新分配所有對象，直到分配穩定。改進的K-Means聚類算法描述如下：

輸入：ε閾值系數；聚類簇個數k；包含N個對象的數據集D。

輸出：k個簇的集合；孤立點集I。

步驟：

(1) 依據定義3所述，從數據集D中抽取樣本數據集S；

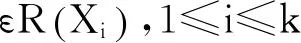
(3)repeat；

(4) 清空孤立點數據集I中的數據；

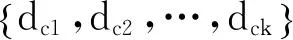
(7) until簇中心不再發生變化。

改進的K-Means算法流程如圖1所示。

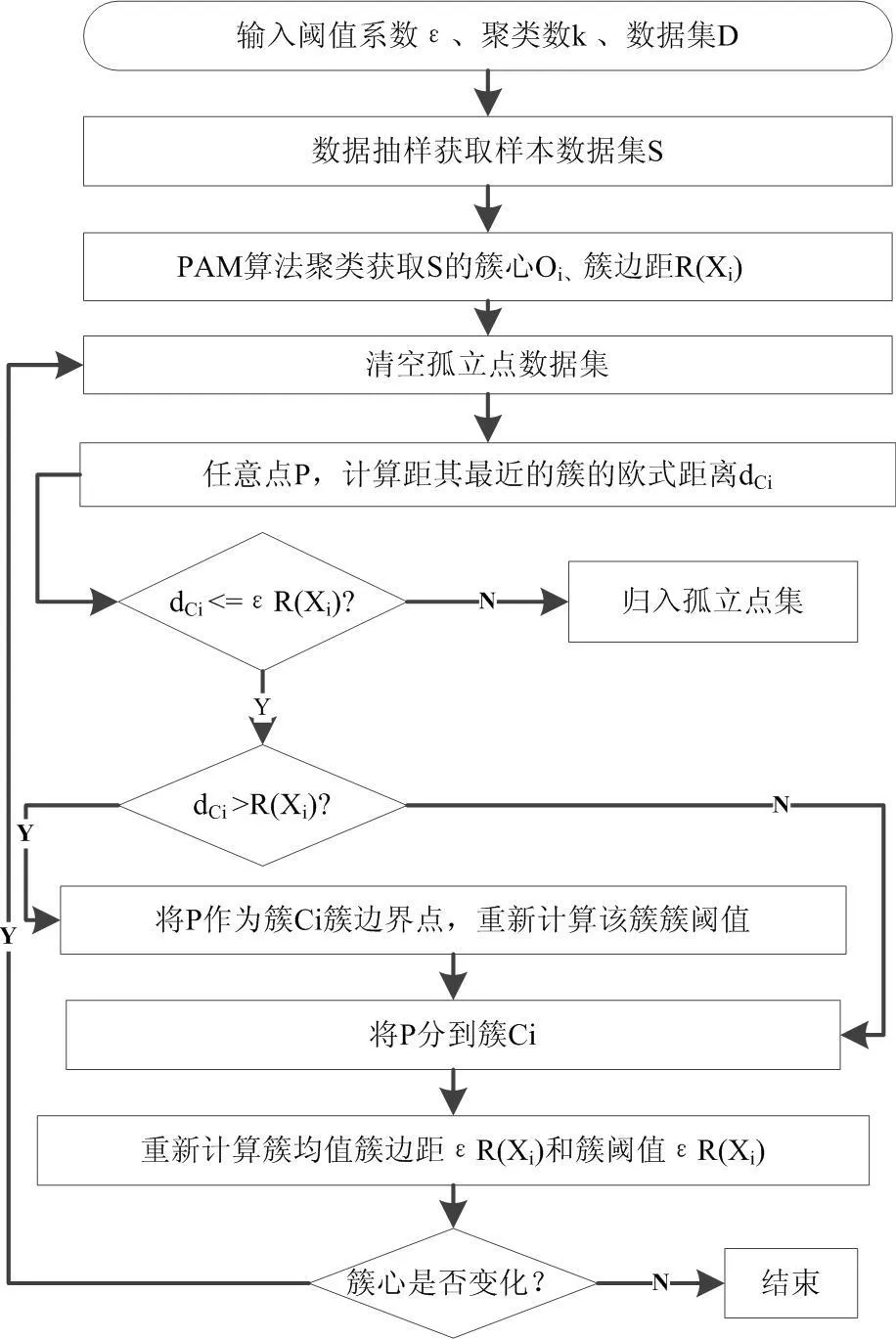
圖1　改進K-Means算法流程圖

3　實驗仿真及分析

實驗環境為 Intel(R) Core(TM)i3-3110M CPU @ 2.40GHz，內存 4 GB，Windows 7系統，實驗工具為Matlab 7。實驗數據為UCI數據庫中iris和waveform數據集，各數據集屬性見表1。為驗證算法處理孤立點的效果，在兩個數據集中添加孤立點數據，使孤立點數據比例達到整個數據集的5%。

表1　實驗數據集屬性

3.1　聚類中心選取驗證

iris數據集實際聚類數據中心分別為setosa{5.00,3.41,1.46,0.24}、versicolor{5.93,2.77,4.26,1.32}、virginica{6.58,2.97,5.55,2.02}。依照定義3，利用PAM算法獲取的樣本數據的聚類中心別為setosa{5.0,3.4,1.5,0.2}、versicolor{5.9,3.0,4.2,1.5}、virginica{6.5,3.0,5.5,1.8}。本文改進的算法獲取的聚類中心與iris數據實際聚類中心的誤差平方和為0.049 1，說明提出的算法獲取的聚類中心與iris數據集真實聚類中心非常接近，能有效代表數據的實際分布。因此，利用本文的算法獲取的聚類中心作為K-Means算法初始聚類中心是可行且較優的。

3.2　準確率和效率比較

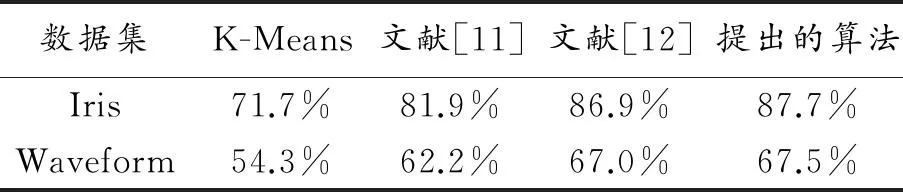
表2是本文提出的算法、傳統K-Means算法、文獻[11]和文獻[12]在iris和waveform數據集上聚類準確率比較結果，其中本文提出的算法的參數設置如下：簇閾值系數 =1.5，聚類數k=3。由于本文提出的算法和文獻[12]的方法不僅對初始聚類中心進行優化，而且對孤立點數據進行了處理，聚類準確率明顯高于傳統K-Means算法和僅對初始聚類中心進行優化的文獻[11]的結果。但從圖2可以看出，文獻[12]需要對孤立點數據進行預處理，因此隨著實驗數據量的不斷增加，算法執行所需要的時間增長趨勢明顯，呈冪指數增長。相比而言，本文提出的算法在聚類過程中同步處理孤立點數據，算法執行時間增長速度平穩，呈線性增長趨勢。綜上可知，本文算法在保持高準確率的同時能顯著提高算法的執行效率。

圖2　算法執行時間比較

4　結束語

數據集中存在的孤立點數據嚴重影響了K-Means算法聚類準確率。為了消除孤立點對聚類質量的影響，提高K-Means算法聚類效果，本文提出了一種基于PAM和簇閾值的改進K-Means算法。該算法利用PAM獲取樣本數據聚類中心作為K-Means算法的初始聚類中心，利用簇閾值方式過濾孤立點數據，消除了孤立點對聚類準確率的影響，具有較高的聚類準確率和執行效率。

[參考文獻]

[1]趙衛中,馬慧芳,李志清,等.一種結合主動學習的半監督文檔聚類算法[J].軟件學報，2012,23(6):1486-1499.

[2]Lingras P,West C.Interval set clustering of web users with rough K-Means[J].Journals of Intelligent Information Systems,2004,23(1):5-16.

[3]Redmond S J,Heneghan C.A method for initialising the K-Means clustering algorithm using kd-trees[J].Pattern Recognition Letters,2007,28(8):965-973.

[4]Li M J,Ng M K, Cheung Y M.Agglomerative fuzzy K-Means clustering algorithm with selection of number of clusters[J].IEEE Transactions on Knowledge and Data Engineering,2008,20(11):1519-1534．

[5]Zhang Y,Zhou H,Qin S.Decentralized fault diagnosis of large-scale processes using multiblock kernel principal component analysis[J].Acta Automatic Sinica,2010,36(4):593-597.

[6]Likas A,Vlassis M,Verbeek J.The global K-Means clustering algorithm[J].Pattern Recognition,2003,36 (2):451-461.

[7]Seinley D,Brusco M J.Initializing K-Means batch clustering:a critical evaluation of several techniques[J].Journal of Classification,2007,24(1):99-121.

[8]侯曉晶,王會青.基于最近鄰距離差的改進孤立點檢測算法[J].計算機工程與設計,2013,34(4):1265-1269

[9]鄭丹,王潛平.K-Means初始聚類中心的選擇算法[J].計算機應用,2012,32 (8):2186-2188,2192.

[10]周董,劉鵬.VDBSCAN:變密度聚類算法[J].計算機工程與應用,2009,45(11):137-153.

[11]蘇錦旗,薛惠鋒,詹海亮.基于劃分的K-均值初始聚類中心優化算法[J].微電子學與計算機,2009,26(1):8-11.

[12]王賽芳,戴芳.基于初始聚類中心優化的K-均值算法[J].計算機工程與科學,2010,44(23):166-168.

[13]雷小鋒,謝昆青,林帆,等.一種基于K-Means局部最優性的高效聚類算法[J].軟件學報,2008,19(7):1683-1692.

[14]畢方明,王為奎,陳龍.基于空間密度的群以噪聲發現聚類算法研究[J].南京大學學報：自然科學版，2012,48(4):491-498.

An Improved K-Means Algorithm Based on PAM Algorithm and Cluster Threshold

Bu Xusong1,Liu Libo1, Shi Lei2

(1.SchoolofMathematicsandComputer,NingxiaUniversity，Yinchuan,Ningxia750021,China;

2.TechniqueCenterofModernEducation,HubeiEngineeringUniversity,Xiaogan,Hubei432000,China)

Key Words：sampling;K-Means cluster; cluster threshold; outlier

(責任編輯：張凱兵)