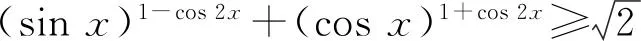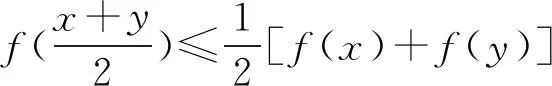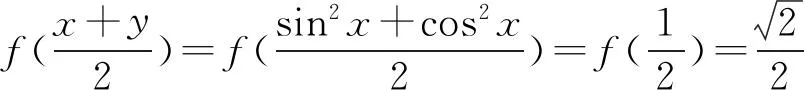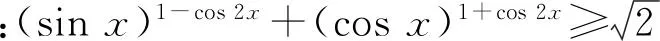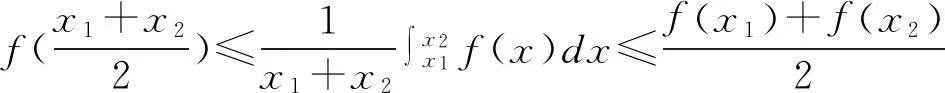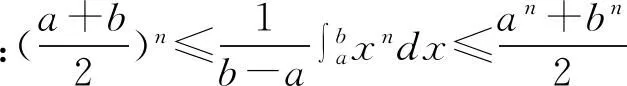凸函數(shù)的積分判別法及其應(yīng)用
曹俊飛
(廣東第二師范學(xué)院 數(shù)學(xué)系,廣東 廣州 510310)
凸函數(shù)的積分判別法及其應(yīng)用
曹俊飛
(廣東第二師范學(xué)院 數(shù)學(xué)系,廣東 廣州 510310)
摘要:凸函數(shù)是一類非常重要的函數(shù),有著廣泛的應(yīng)用,因此對(duì)凸函數(shù)的研究具有重要意義。本文首先建立了凸函數(shù)的積分判別法,并給出了此判別法與凸函數(shù)其他定義之間的等價(jià)關(guān)系。然后介紹了積分判別法中的Hadamard不等式,并證明了Hadamard不等式中等號(hào)成立的充分必要條件。最后舉例說(shuō)明了凸函數(shù)積分判別法的運(yùn)用方法。
關(guān)鍵詞:凸函數(shù);積分判斷法;Hadamard不等
中圖分類號(hào):O174
文獻(xiàn)標(biāo)志碼:碼:A
文章編號(hào):號(hào):2095-4824(2015)03-0098-05
收稿日期:2015-03-11
作者簡(jiǎn)介:曹俊飛(1982-),男,湖北黃岡人,廣東第二師范學(xué)院數(shù)學(xué)系講師,博士。
Abstract:Convex functions are a very important kind of functions which are been widely used in mathematical and other fields. Hence it is of great significance to study the judgment method of convex functions. First, this paper establishes the integral judgment method of convex functions and proves the equivalence between this theorem and other definitions of convex functions. Next it introduces the Hadamard inequality and proves the necessary and sufficient conditions for the medium-Hadamard inequality. Finally, several examples of the convex function application with the integral method are illustrated.
凸函數(shù)的定義最早是在1905年由Jensen給出的,自凸函數(shù)理論建立以來(lái),凸函數(shù)這一重要概念已在許多數(shù)學(xué)分支中得到了非常廣泛的應(yīng)用。眾多學(xué)者對(duì)凸函數(shù)的研究對(duì)其發(fā)展起著十分重要的作用。
作為數(shù)學(xué)中一個(gè)比較年輕的數(shù)學(xué)分支,凸函數(shù)是在上世紀(jì)50年代以后隨著數(shù)學(xué)規(guī)劃、最優(yōu)化控制、數(shù)理經(jīng)濟(jì)學(xué)等應(yīng)用數(shù)學(xué)學(xué)科的興起而發(fā)展起來(lái)的[1]。到目前為止,凸函數(shù)的研究已經(jīng)從凸函數(shù)的定義研究到更多的關(guān)于凸函數(shù)性質(zhì)的研究以及凸函數(shù)性質(zhì)的應(yīng)用方面的研究。由于凸函數(shù)的理論的廣泛性以及在數(shù)學(xué)各個(gè)領(lǐng)域的廣泛應(yīng)用,因此對(duì)凸函數(shù)理論進(jìn)一步深入研究和推廣顯得尤為重要,對(duì)凸函數(shù)的判別、性質(zhì)以及應(yīng)用的研究具有十分重要的意義。
基于Jensen凸函數(shù)的定義和性質(zhì), 1893年Hadamard給出了經(jīng)典的Hadamard不等式。Hadamard不等式是隨著凸函數(shù)的發(fā)展而逐漸發(fā)轉(zhuǎn)起來(lái)的,它是凸函數(shù)理論以及應(yīng)用的重要組成部分。一直以來(lái)關(guān)于凸函數(shù)Hadamard不等式理論和應(yīng)用的研究也一直是不等式和凸函數(shù)理論和應(yīng)用研究的熱點(diǎn)問(wèn)題。
本文首先建立了凸函數(shù)的積分判別法,并給出了此判別法與凸函數(shù)其他定義之間的等價(jià)關(guān)系。然后介紹了積分判別法中的Hadamard不等式并證明Hadamard不等式中等號(hào)成立的充分必要條件。最后舉例說(shuō)明了凸函數(shù)積分判別法的應(yīng)用實(shí)例。
1 預(yù)備知識(shí)
凸函數(shù)的定義最先是由Jensen所引入,定義如下:
定義1[2]若函數(shù)f(x)滿足

(1)
則稱f(x)為凸函數(shù)。
后來(lái)一些作者給出了如下的一般定義:
定義2[3]若函數(shù)f(x)滿足
f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)
(2)
則稱f(x)為凸函數(shù)。
注:若f(x)是區(qū)間I上的連續(xù)函數(shù),則上述兩個(gè)凸函數(shù)的原始定義是等價(jià)的[2]。
凸函數(shù)還有很多等價(jià)的定義:
定義3[2]如果對(duì)?x1,x,x2∈I,x1 則稱f為I內(nèi)的凸函數(shù)。 則稱f為I內(nèi)的凸函數(shù)。 定義5[2]如果對(duì)?x1,x2∈I,x1 則稱f為I內(nèi)的凸函數(shù)。 定義6[2]若函數(shù)f(x)滿足 (1)?x∈I,f′-(x),f′+(x)存在,且f′-(x)≤f′+(x); (2)?x1,x2∈I,x1 則稱f為I內(nèi)的凸函數(shù)。 定義7[2]若果函數(shù)f(x)滿足在I內(nèi)存在單調(diào)增加的函數(shù)φ,?x0∈I,?x∈I, 則稱f為I內(nèi)的凸函數(shù)。 定義8[4]若對(duì)?x1,x2,…,xn∈I,函數(shù)f(x)滿足 則稱f為I內(nèi)的凸函數(shù)。 定義9[5]若函數(shù)f(x)滿足在I內(nèi)可導(dǎo),且對(duì)?x,y∈I,有 f(x)≥f′(y)(x-y)+f(y), 則稱f為I內(nèi)的凸函數(shù)。 定義10[6]設(shè)函數(shù)f(x)在I內(nèi)連續(xù),且二次可導(dǎo),f″(x)≥0,則稱f為I內(nèi)的凸函數(shù)。 定義11[7]若對(duì)?x1,x2∈I,函數(shù)f(x)滿足 φ(λ)=f[λx1+(1-λ)x2],為[0,1]上的凸函數(shù),則稱f為I內(nèi)的凸函數(shù)。 定義12[5]若函數(shù)f(x)滿足在I內(nèi)可導(dǎo),且f′(x)單調(diào)遞增,則稱f為凸函數(shù)。 本節(jié)將建立凸函數(shù)的積分判別法。 定理1 若對(duì)任何a 則f為凸函數(shù)。 定理2 若對(duì)任何a 則f為凸函數(shù)。 注:上述兩個(gè)積分不等式稱為Hadamard不等式。 證明:(1) 證明第一條不等式: 令 x=x1+λ(x2-x1),λ∈(0,1) 則 同理,令 x=x2-λ(x2-x1),λ∈(0,1), 有 從而 綜上可得: 與已知不等式 相矛盾。故可知f是凸函數(shù)。 (2) 證明第二個(gè)不等式: 令x=x1+λ(x2-x1),λ∈(0,1),則有: 假設(shè)f不是凸函數(shù),則: f[x1+λ(x2-x1)]=f[λx2+(1-λ)x1]>λf(x2)+(1-λ)f(x1) 所以: 與已知不等式 上述兩個(gè)積分不等式可以判斷一個(gè)函數(shù)是不是凸函數(shù),由此建立凸函數(shù)的積分判別法。通過(guò)建立積分判別法,使得函數(shù)在微積分學(xué)有了更加充分的作用。 命題1若函數(shù)f(x)滿足在I上連續(xù),則可以由定義11?定理1。 證明:對(duì)?x1,x2∈I,由于 φ(λ)=f[λx1+(1-λ)x2]為[0,1]上的凸函數(shù),所以: f[λx1+(1-λ)x2]=φ(λ)=φ·1+(1-λ)·0] ≤λφ(1)+(1-λ)φ(0)=λf(x1)+(1-λ)f(x2) 所以f為凸函數(shù)。 即得到 命題2若函數(shù)f(x)在I內(nèi)可導(dǎo),則可以由定義9?定理2. 證明:函數(shù)f在I內(nèi)有定義,且f在I內(nèi)可導(dǎo),若f為I上的凸函數(shù),則: 由定義9可知:?x,y∈I,y f(x)≥f(y)+f′(y)(x-y), 則 而 又因?yàn)?/p> 所以 即 則 所以命題得證。 通過(guò)以上的證明可知,本文建立的凸函數(shù)積分判別法與已有的定義是等價(jià)的,從而說(shuō)明本文建立的定理的正確性。 設(shè)函數(shù)f(x)是區(qū)間[a,b]上的凸函數(shù),則對(duì)于a≤x1 僅當(dāng)f為線性函數(shù)時(shí)等號(hào)成立,它說(shuō)明在Jensen不等式的兩端之間可以用積分的平均值插入[8]。由此得出以下兩個(gè)性質(zhì): 定理3若函數(shù)f(x)在[a,b]內(nèi)連續(xù),且為區(qū)間上的凸函數(shù),則: (3) 成立的充要條件是:在[a,b]上,有 (4) 證明:充分性:對(duì)(4)式兩端從a到b積分, 所以: 必要性:因?yàn)閒是凸函數(shù),按照凸函數(shù)的定義3,可知 (5) 特別地,取x1=a,x2=b,則(5)可以化成: (6) 上式左邊是連續(xù)函數(shù),對(duì)其積分可以得到: 所以: 所以在[a,b]上, 必要性得證。 定理4若函數(shù)f(x)在[a,b]內(nèi)連續(xù),且為區(qū)間上的凸函數(shù),則: (7) 的充要條件是:在[a,b]上,有 (8) (9) 對(duì)(8)式兩端從a到b積分,可以得到: 所以可以得到: 可見(jiàn)充分性得證。 也就是說(shuō): 上式左邊是連續(xù)函數(shù),所以對(duì)其積分可得: 所以可以得到: 在上式中,取x=a,即可以得到: 同理:再對(duì)(6)式左邊積分,得 所以: 所以在[a,b]上, 即必要性得證。 注:定理3連續(xù)的條件不能去掉。 證明:原不等式等價(jià)于: 設(shè)f(x)=xx,則由凸函數(shù)的積分判別法知f(x)為(0,∞)上的凸函數(shù),故當(dāng)x>0,y>0時(shí), 令x=sin2x,y=cos2x,則: 例2a>0,b>0,n∈N+且n≠1,則有以下均值關(guān)系: 證明:設(shè) f(x)=xn,x∈(0,+∞),f″(x)=n(n-1)xn-2>0, 所以f為凸函數(shù)。即對(duì)任意的正數(shù)有: 可以得到: 證畢。 [參考文獻(xiàn)] [1]華東師范大學(xué)數(shù)學(xué)系.數(shù)學(xué)分析[M].北京:高等教育出版社,2010. [2]劉國(guó)華, 陳妍, 龐培林,等. 關(guān)于凸函數(shù)的八個(gè)等價(jià)定義[J]. 河北建筑科技學(xué)院學(xué)報(bào):自然科學(xué)版, 2003, 20(3):82-83. [3]華東師范大學(xué)數(shù)學(xué)系,數(shù)學(xué)分析[M]. 北京:高等教育出版社, 1980. [4]俞文輝.凸函數(shù)不同定義間的關(guān)系及其應(yīng)用[J]. 南昌高專學(xué)報(bào), 2005, 60(5):112-113. [5]郭素霞.關(guān)于凸函數(shù)定義的討論[J]. 衡水師專學(xué)報(bào), 2000, 2(4):49-52. [6]尹傳勇.凸函數(shù)的等價(jià)命題[J].中國(guó)高等教育論壇,1998,10(2):21-24. [7]鐘偉, 周彬林. 凸函數(shù)的幾種不同定義及作用[J]. 九江學(xué)院學(xué)報(bào):哲學(xué)社會(huì)科學(xué)版, 2007, 26(3):74-77. [8]匡繼昌. 常用不等式[M]. 3版.濟(jì)南: 山東科學(xué)技術(shù)出版社, 2004. Integral Judgment Method of Convex Function and Its Applications Cao Junfei (DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou,Guangdong510310,China) Key Words:convex function;integral judgment method;Hadamard inequality (責(zé)任編輯:張凱兵)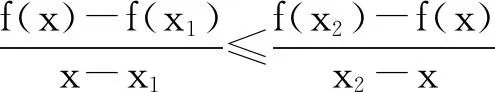
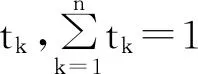




2 凸函數(shù)積分判別法
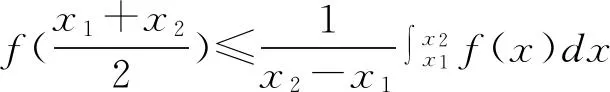
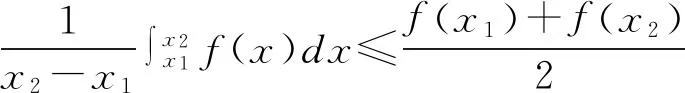


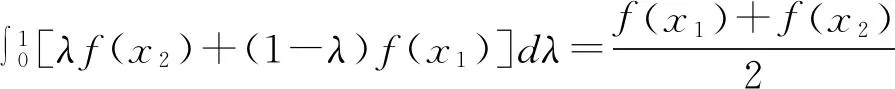
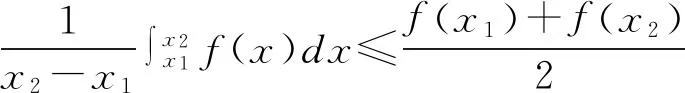
3 凸函數(shù)積分判別法與凸函數(shù)其他定義的關(guān)系



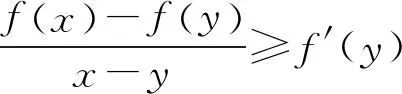


4 Hadamard不等式等號(hào)成立的充要條件
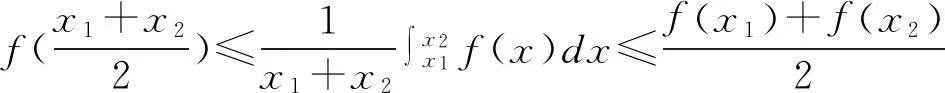




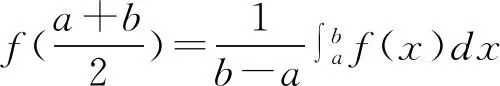


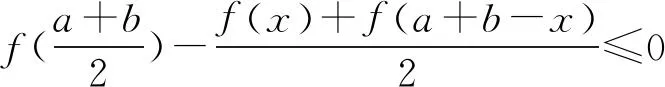



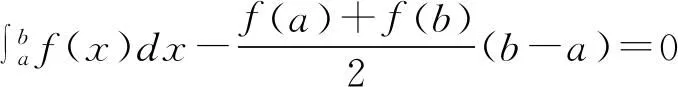


5 應(yīng)用