補形
2015-12-12 05:41:21崔磊
新課程·中學 2015年11期
崔磊

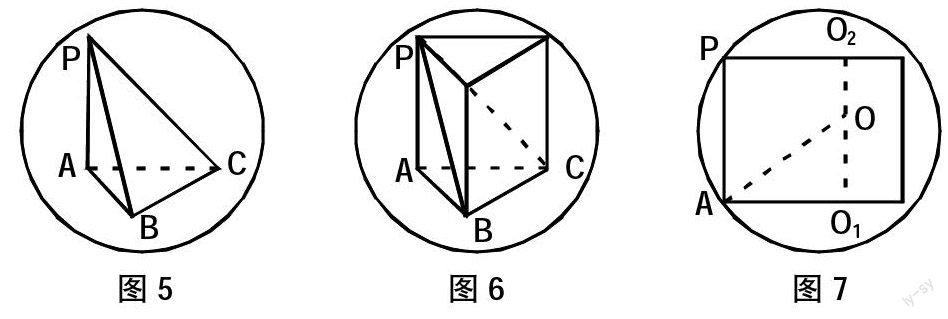
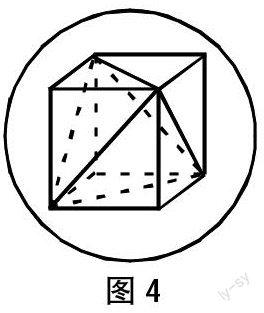
在立體幾何的學習中,經常遇到求解三棱錐外接球體半徑的問題,此類問題往往球心的位置難以找到。我們知道,棱錐是柱體的一部分,因此,在求三棱錐外接球體的半徑時,通過“補形”,將錐體還原成柱體,有時能起到柳暗花明的效果。常見的“補形”方法有下列幾種.
例1.已知三棱錐P-ABC中,PA⊥PB,PB⊥PC,PC⊥PA,且PA=3,PB=4,PC=5.則其外接球體的表面積為 .
思路:補成“長方體”
總之,“補形”是求解三棱錐外接球體半徑的一條重要途徑,且通常可補成上述幾種模型。“補形”應遵循“擁有相同的外接球體”的原則,在此基礎上,還要選擇好恰當的位置作出截面,將抽象的空間問題轉化為熟悉的平面問題,關系也就簡單明朗多了。

