基于聚類模型預測的無線傳感網自適應采樣技術研究

張美燕 蔡文郁 周麗萍

1 引言

近年來，隨著微機電一體化、短距離無線通信、互聯網絡等技術的迅速發展，一種全新的信息獲取和處理技術 無線傳感網（WSNs）應運而生。無線傳感網是由大量無處不在的、具有無線通信與計算能力的微小傳感器節點構成的自組織分布式多跳通信網絡系統，是能根據環境自主完成指定任務的“智能”協同系統[1,2]。無線傳感網實現了大量分布式時空數據的高保真采樣，但在一般應用中傳感器節點的采樣頻率通常是固定的，而自適應采樣技術的采樣頻率可根據被測對象的變化而變化，當觀測對象變化趨勢慢時降低采樣頻率，當觀測對象變化趨勢較快時提高采樣頻率。本文研究了一種基于聚類預測模型的無線傳感網自適應采樣技術，所有的傳感器節點根據數據梯度關系劃分成多個聚類，算法選舉了各個聚類中的簇頭節點。簇頭節點根據感知數據的歷史模型和當前采樣數據進行判決，根據是否滿足采樣精度需求，進而利用“乘增半減”的采樣頻率更新策略調整所有簇成員節點的采樣頻率。如果聚類內傳感采樣數據的動態性比較低，則降低采樣頻率以減少冗余數據的產生與傳輸，如果傳感采樣數據的動態性比較高，則提高數據采樣頻率從而保證數據采樣質量，由此實現網絡能率高效與數據采集質量兩者之間的均衡性。

目前相關研究工作大概都基于如下假設：（1）在無線傳感網的實際應用場景中，傳感器節點采集到的采樣數據通常是連續的，從總體上表現出一定的連續性和穩定性；（2）受無線多跳通信不可靠、傳感器節點失效以及節點能量的限制，感知數據的獲取、處理與傳輸必然存在一定范圍的誤差值。因此，無線傳感網所獲取的數據集在時間域和空間域上都是無限的，實際上只能通過抽樣獲取所需的數據內容，而且所獲得的數據并非實際的精確值，因此收集到的數據越多并不意味著結果越精確?；谏鲜鲞@種思想，有一些研究者開啟了無線傳感網中數據采樣優化技術的研究。無線傳感網數據處理方法一般采用先進行網內數據處理然后再匯聚傳輸的方式以減少所需傳輸的數據量。目前網內數據處理可分為數據近似代替（data approximation）和數據匯聚處理（data aggregation）兩種方法[3]：數據近似代替通過對感知數據進行分布式建模，大量減少感知數據的傳輸量，從而延長網絡生存周期。數據近似代替方法可基于不同模型：概率模型[4]，時間序列分析模型[5]，數據挖掘模型[6]和數據壓縮模型[7]。數據匯聚處理使用AVG, TOP, COUNT, SUM等聚集函數來降低感知數據的傳輸量，但存在的最大問題是感知數據中大量的原始信息丟失，只能提供較為粗糙的統計結果量。

與本文想法較為相近的有以下研究：文獻[8]提出傳感器節點的采樣時間間隔由Sink節點根據帶寬來分配，通過Kalman濾波預測下一時刻采樣值，如果預測值和真實值的誤差大于預設閾值，則根據當前誤差調整采樣時間間隔，但該方法沒充分利用感知數據的相關性；文獻[9]提出了一種利用線性回歸模型來動態調整采樣頻率的策略，在單個傳感器節點上設置預測模型，根據實際采樣數據域期望值之間的差異大小來調整采樣頻率，但是該方法增加了節點之間的通信負荷；文獻[10]提出了一種根據數據空間相關性選擇聚集域中采樣節點的方法，數據相關性較強的節點中，只有遴選出的某些特殊節點需要采集感知數據，因此降低了數據間的冗余，但是該方法并未考慮時間域采樣頻率的調整；文獻[11]提出一種在Nyquist采樣頻率基礎上的時間域采樣頻率的跟隨調整，但是節點之間的額外通信所需耗費很多能量。文獻[12]提出了一種基于預測模型的無線傳感網內數據糾錯方法，在時間域建立誤差模型，以提高感知數據的可靠性。針對以上算法的不足之處，本文引入時間域數據預測模型技術，從而在分布式聚類內實現自適應采樣，提高網絡能效水平。文獻[13]創新地將自適應采樣的算法應用于無線體感網（body sensor networks）中，考慮了無線體感網的特殊限制和需求。

2 預測模型匹配自適應采樣算法

2.1 算法原理

本文所研究的基于感知數據預測模型的自適應采樣技術中，首先將傳感器節點根據數據梯度關系劃分成多個聚類，各個聚類中的簇頭節點根據感知數據的歷史模型和當前采樣數據的變化情況決定聚類內所有成員節點的采樣頻率（即下一采樣時刻），只有當真實值（以高頻率采樣的實測值為準）與預測值的誤差大于預設閾值時，簇頭節點才提高節點采樣頻率，實現網絡能率高效及數據精度質量之間的均衡。當感知數據的動態性較高時，提高采樣頻率從而保證采樣質量，當感知數據的動態性較低時，根據數據歷史模型，僅發送那些必需發送的數據，降低采樣頻率以減少冗余數據的產生與傳輸。

本文算法的主要原理如下：每個聚類內的簇頭節點根據聚類內成員節點的歷史數據建立一個預測模型，用預測模型估計的估計值來代替采樣數據，并用較低頻率的采樣數據來更新預測模型，如圖 1所示。

當采樣數據與估計數據差較大時，逐步增大采樣頻率；否則，逐步降低采樣頻率。每個聚類內簇頭節點的在線數據預測模型框架如圖2所示。通過歷史數據的模型特征提取建立預測樹，當數據與預測模型不一致時進行采樣頻率的更新調整。

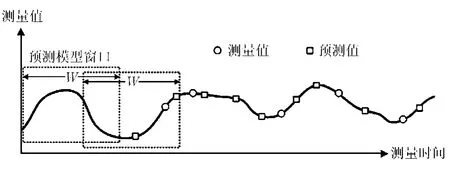
圖 1 算法原理

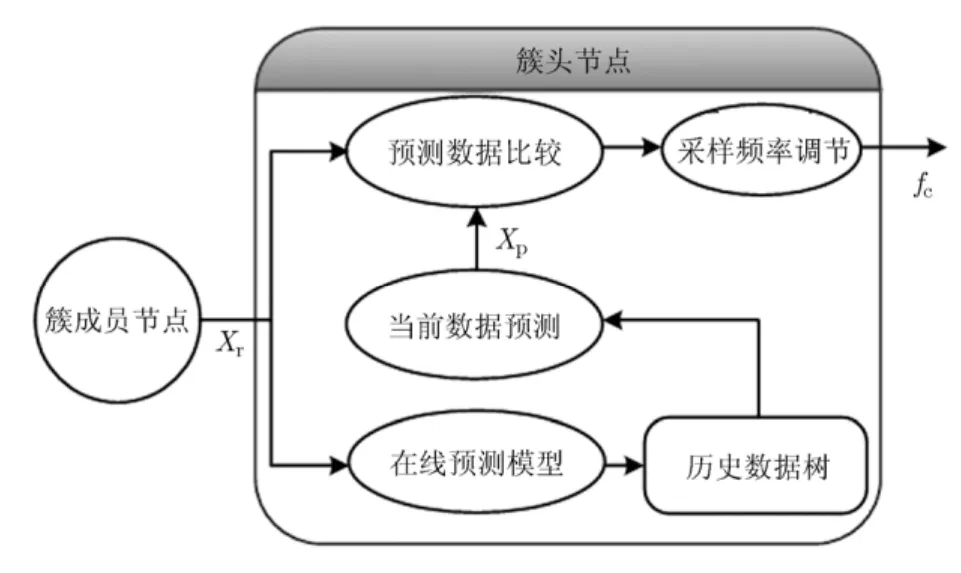
圖 2 每個聚類內集中式預測模型

但是預測模型與特定的應用場景有著很強的相關性，而Weiner和Kalman濾波器等預測計算方法對傳感器節點而言過于復雜。本文中各個聚類中簇頭節點所采用的預測模型采用計算量較小的線性自回歸（Auto Regressive, AR）模型，并采用遞歸最小二乘（LS）估計方法進行參數估計。如式（1）和式（2）所示：

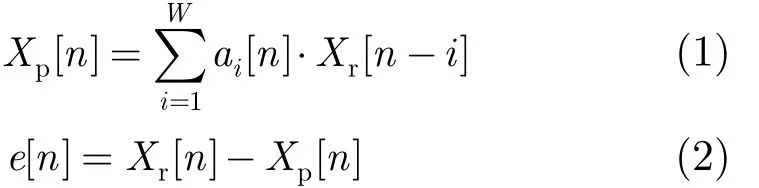
其中 Xp[ n]是預測數據值，Xr[ n]是實測數據值，e[ n]是誤差值， ai[ n]是AR模型的各階系數。

2.2 數據相關性聚類機制

數據相關性聚類機制的主要思路是將數據相關度較強（體現為物理空間位置和數據均值較為接近）的傳感器節點歸在一個簇，每個聚類內的傳感器節點進行集中式的數據模型預測，簇頭節點負責維護每個聚類內的數據預測模型，減低需傳輸的冗余數據，提高能量使用效率。每個傳感器節點成為簇頭節點的概率計算如下：節點以自身剩余能量和其一跳鄰居數（節點度數）的綜合權值作為最大概率值來實施簇頭節點的選舉，則最大概率值公式為

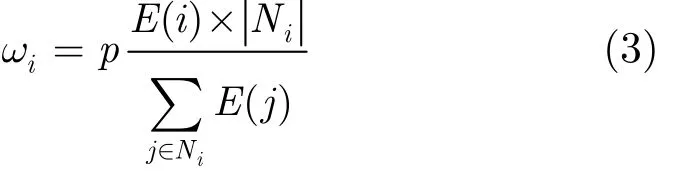
式（3）中p代表簇頭節點所占的比率， p ∈ （ 0,1]，實際上簇頭節點所占總節點數的上限比率一般設為20%，因此 p ∈ （ 0,0.2]; E （ i）是節點 Ni的剩余能量，Ni是節點 Ni的度數（包含自身）。

一旦傳感器節點被選舉為簇頭節點，立即在其一跳鄰居節點內廣播簇頭標志信息，誘導非簇頭節點加入自身簇。非簇頭節點選擇最優簇頭節點的思想如下：選擇簇頭節點與簇成員節點之間數據梯度值最小的一跳鄰居簇頭作為簇頭節點。如圖3所示。

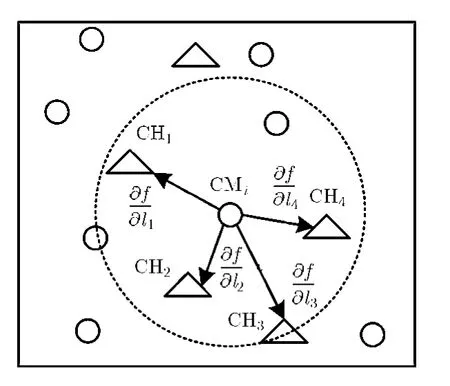
圖3 基于數據梯度的簇頭節點遴選示意圖

假設非簇頭節點CMi有4個簇頭節點（C H1,CH2, C H3, C H4）可供選擇，各個方向的數據梯度值如式（4）所示。這部分的研究可以參考作者已發表的會議論文[14]。

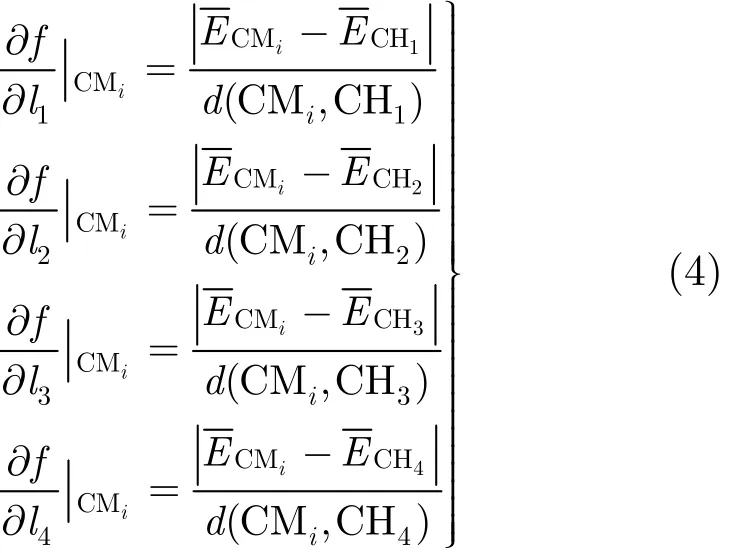
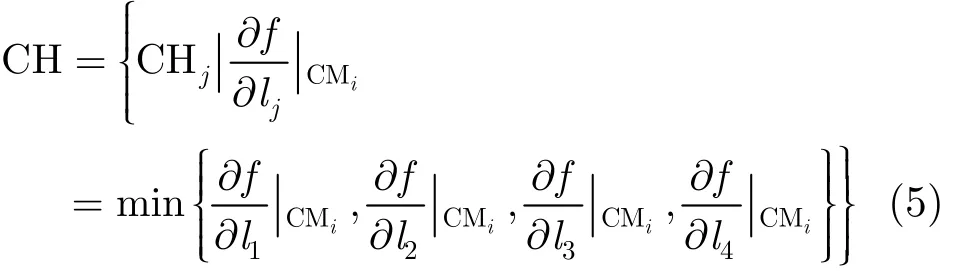
綜上所示，本文提出的聚類機制充分考慮了感知數據相關性以及傳感器節點空間位置，形成的簇分布能夠體現感知數據的空間關聯性。

2.3 數據預測模型及方法

根據平穩數據預測精度和速度的需求，本文采用二階AR預測模型，預測值如式（6）如下：

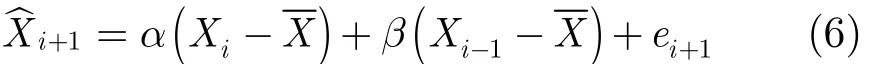
其中 Xi為真實值，α和β為AR模型的參數，ei+1為預測誤差，X是W個歷史觀測數據的均值。對于給定的W個歷史數據，參數α和β可由樣本自相關函數計算得出。

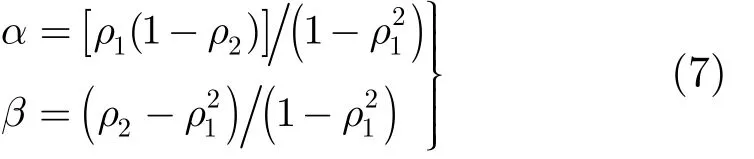
而樣本自相關函數的計算可由式（8）得到：

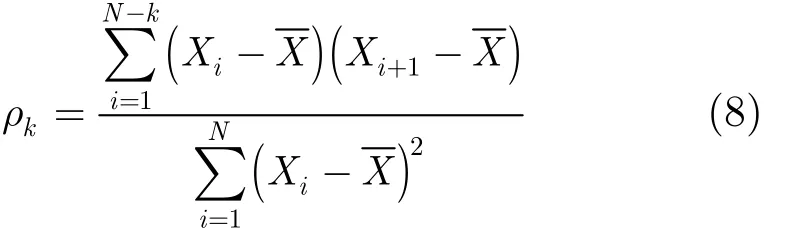
可見，預測誤差可以由預測值和真實值之差得到：

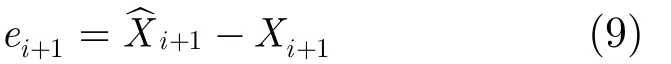
本文中的數據預測模型沒有采用定期更新的機制，因為定期更新會引入不必要的更新次數，只有當誤差大于一定閾值時才啟動重新計算二階AR系數的過程。AR模型參數估計采用了常用的Yule-Walker方程法[15]。

2.4 采樣頻率更新機制

采樣頻率的自適應調整采用加增半減的方法來進行調整：當采樣誤差小于預設閾值時，減半聚類中各個傳感器的采樣頻率，否則增加采樣頻率，增加的步進值為上限閾值和下限閾值的M分之一。最后限制調整過的采樣頻率在上限閾值和下限閾值范圍之內。為了衡量誤差的精度，預測誤差采用了平均相對誤差 （Mean Relative Error, MRE）指標來表征預測數據偏離實際數據的程度。

其中W為數據窗口長度，本文根據所采用數據集的采樣頻率屬性，各個參數值設置為

采樣頻率更新策略如表1所示。

表1 采樣頻率更新策略

2.5 頻率更新機制分析

采樣頻率的自適應調整由各個聚類中的簇頭節點管理，簇頭節點在接收到采樣數據后將下一個采樣頻率附帶在確認數據包中發送給各個簇成員節點。由于簇頭節點接收到感知數據后也會發送確認數據包，因此采樣頻率的更新并不花費額外的通信負荷。各個聚類內數據采集的頻率不一樣，但是簇頭節點可以通過模型預測的方法以統一的頻率將數據上傳到匯聚節點。

3 仿真

本文采用Berkeley大學的Intel實驗室[16]所做的真實采樣數據，這份數據來自于54個傳感器，有溫度、濕度、亮度以及電壓等讀數，大約每隔30 s從54個傳感器讀取一次數據，共有一個月的數據，本文仿真只采用了其中溫度值數據。本文定義了不同滑動窗口長度的數據序列相關性系數的量化公式：

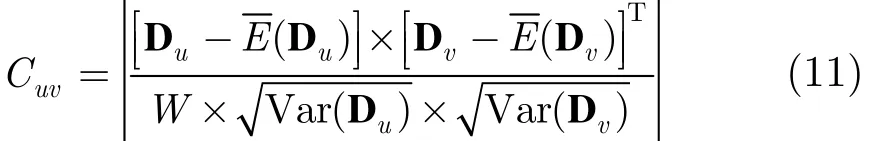
式（11）中 Cuv是窗口長度為W 的數據序列 Du和 Dv的相關性系數，E（Du）和Var（Du）分別表示數據序列Du的均值和均方差。Cuv∈[-1 , 1]，其中 Cuv=-1代表數據序列 Du和 Dv負相關，Cuv= 0 代表數據序列Du和 Dv不相關， Cuv= 1 代表數據序列 Du和 Dv正相關。以一天數據量為窗口長度（W=1100），節點1與節點2的相關性系數為0.9393，節點1與節點16的相關性系數為0.7199，節點1與節點2的相關性明顯高于節點1與節點16的相關性系數。

當簇頭比例分別為 p =0.05和p= 0 .15時，數據相關性聚類結果如圖4所示，不同聚類采用不同形狀的節點集表示，其中標志節點號的為每個簇相應的簇頭節點。

如圖5所示，可以看到節點1在2004年3月1日～3月6日的溫度數據變化趨勢在時間維度上傳感器節點的數據呈現很強的重復性，因為在時間維度上可以利用各個聚類內傳感器節點采樣頻率的自適應調整進行網絡能耗優化。當采樣頻率分別為=1次/10min = 0 .1 ×Hz時，節點2在2004年3月1日的實測數據、預測數據和估計誤差分別如圖6所示。

假設節點能耗主要考慮由采樣過程所產生，因此網絡整體能耗體現在傳感器數據的采樣頻率上，數據采樣頻率越高，網絡能耗越大。在平均相對誤差θMRE=5%和簇頭比例 p = 0 .2的條件下，利用數據相關性聚類機制獲得的聚類劃分結果為 9個聚類，每個時刻所有聚類的采樣頻率平均值如圖7所示。由圖7可以發現，相比固定采樣頻率方式（采樣頻率為Th =1次/1min =1 ×Hz），本文提出的

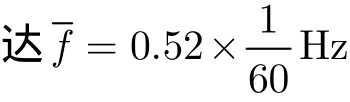
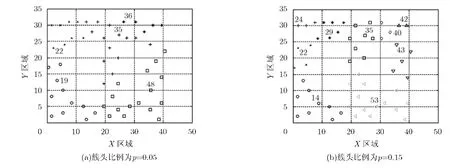
圖4 數據相關性聚類劃分結果

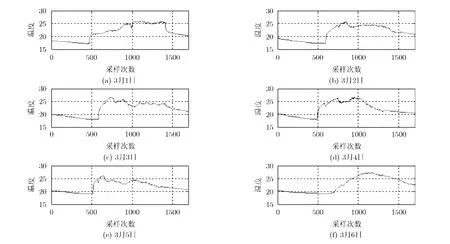
圖5 節點1在不同天的溫度數據變化趨勢

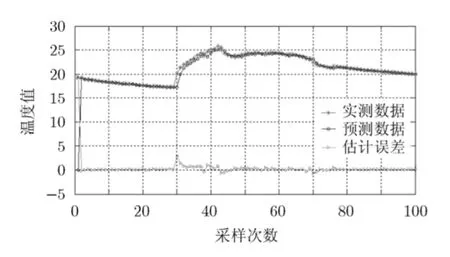
圖6 AR預測誤差分析

4 結束語

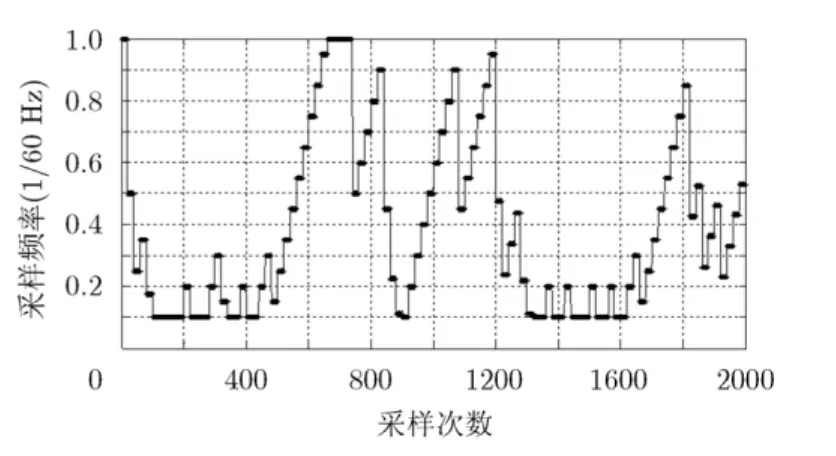
圖7 采樣頻率自適應調整值

本文利用無線傳感網的數據空間相關性，提出了一種基于數據梯度的聚類機制，簇頭節點維護簇成員節點的數據時間域AR預測模型，在聚類范圍內實施基于預測模型的采樣頻率自適應調整算法。通過自適應優化調整采樣頻率，提高無線傳感網的能耗水平：如果感知數據的動態性較高，提高采樣頻率從而保證采樣數據質量，如果感知數據的動態性較低，僅僅發送那些必需發送的數據，降低采樣頻率以減少冗余數據的產生與傳輸。本文屬于一種考慮空間相關性的時間域采樣頻率調整算法，由于綜合考慮了感知數據的時空聯合相關性等特點，因此在提高能耗水平方面具有較大優勢。

[1] Li J Z and Gao H. Survey on sensor network research[J].Journal of Computer Research and Development, 2008, 45（1）:1-15.

[2] 蔡文郁, 張美燕, 蔣一波. 基于時空聯合性的無線傳感網覆蓋采樣技術[J]. 傳感技術學報, 2013, 26（2）: 260-265.Cai Wen-yu, Zhang Mei-yan, and Jiang Yi-bo. Coverage sampling technology based on spatial temporal joint union for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2013, 26（2）: 260-265.

[3] Deligiannakis A, Kotidis Y, and Roussopoulos N.Dissemination of compressed historical information in sensor networks[J]. The VLDB Journal, 2007, 16（4）: 439-461.

[4] Masoum A, Meratnia N, and Havinga P J M. An energy-efficient adaptive sampling scheme for wireless sensor networks[C]. The 8th IEEE International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, Australia, 2013: 231-236.

[5] Tulone D and Madden S. PAQ: time series forecasting for approximate query answering in sensor networks[C].Proceedings of the 3rd European conference for Wireless Sensor Networks （EWSN 2006）, Zurich, Swiss, 2006: 21-37.

[6] Sachidananda V, Khelil A, Noack D, et al.. Information quality aware co-design of sampling and transport in wireless sensor networks[C]. The 6th Joint IFIP Wireless and Mobile Networking Conference （WMNC 2013）, USA, 2013: 1-8.

[7] Zhou S W, Lin Y P, Zhang J M, et al.. A wavelet data compression algorithm using ring topology for wireless sensor networks[J]. Journal of Software, 2007, 18（3）: 669-680.

[8] Jain A and Chang E Y. Adaptive sampling for sensor networks[C]. Proceedings of the 1st International Workshop on Data Management for Sensor Networks （DMSN’04）,Toronto, Canada, 2004: 10-16.

[9] Li Jin-bao and Li Jian-zhong. Data sampling control,compression and query in sensor networks[J]. International Journal of Sensor Networks, 2007, 2（1）: 53-61.

[10] Aplippi C, Anastasi G, Francesco M D, et al.. An adaptive sampling algorithm for effective energy management in wireless sensor networks with energy-hungry sensors[J]. IEEE Transactions on Instrumentation and Measurement, 2010,59（2）: 335-344.

[11] Gedik B, Liu L, and Yu P S. ASAP: an adaptive sampling approach to data collection in sensor networks[J]. IEEE Transactions on Parallel Distributed Systems, 2007, 18（12）:1766-1783.

[12] Mukhopadhyay S, Schurgers C, Panigrahi D, et al..Model-based techniques for data reliability in wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2009,4（8）: 528-542.

[13] Qi Xin, Keally M, Zhou Gang, et al.. AdaSense: adapting sampling rates for activity recognition in body sensor networks[C]. IEEE 19th Real-Time and Embedded Technology and Applications Symposium （RTAS）,Philadelphia, USA, 2013: 163-172.

[14] Zhang Mei-yan, Cai Wen-yu, and Zhou Li-ping. A sensing data Ddriven clustering algorithm for adaptive sampling in wireless sensor networks[C]. 2012 International Applied Mechanics, Mechatronics Automation Synposium（IAMMAS2012）, Shenyang, China, 2012: 748-752.

[15] Da Silva S, Dias J Nior M and Lopes Junior V. Damage detection in a benchmark structure using AR-ARX models and statistical pattern recognition[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2007, 29（2）:174-184.

[16] Samuel Madden: Intel Berkeley Research Lab[OL].http://www.intel-research.net/berkeley/index.asp. 2014.1.