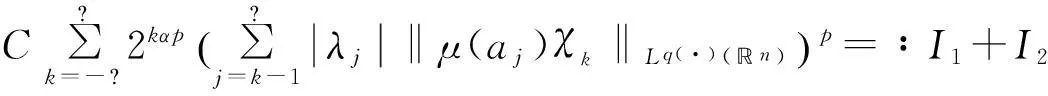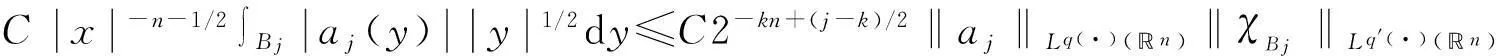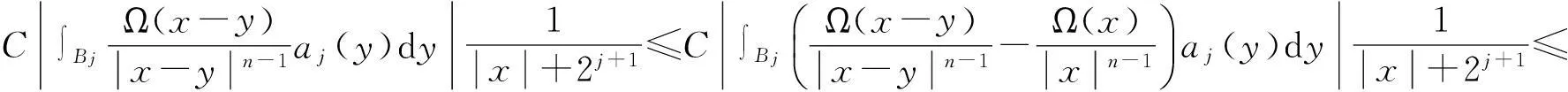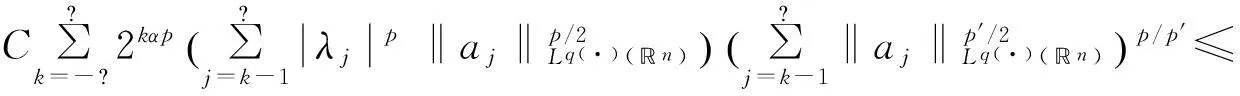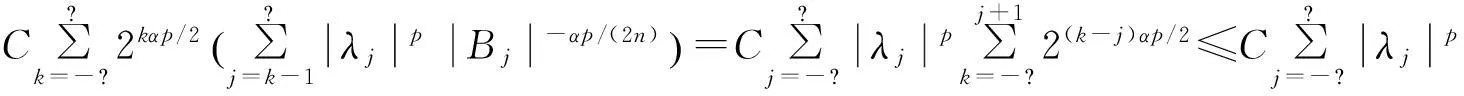變指標Herz型Hardy空間上的Marcinkiewicz積分
王洪彬
(淄博師范高等專科學校 數理科學系,山東 淄博 255130)
?
變指標Herz型Hardy空間上的Marcinkiewicz積分
王洪彬
(淄博師范高等專科學校 數理科學系,山東 淄博 255130)
摘要:Marcinkiewicz積分是調和分析中的重要算子,其有界性研究一直是調和分析中的重要課題之一. 應用其在變指標Lebesgue空間中的有界性以及變指標Herz型Hardy空間上的原子分解定理, 證明了Marcinkiewicz積分算子在齊次和非齊次變指標Herz型Hardy空間上的有界性.
關鍵詞:Marcinkiewicz積分;變指標;Herz型Hardy空間;有界性

1 預備知識和記號
賦予如下Luxemburg-Nakano范數
則Lp(?)(Ω)是Banach空間, 稱之為變指標Lp空間.
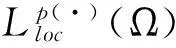
p(·)∶Ω→[1,)的集合, 使得p-=essinf{p(x)∶x∈Ω}>1,p+=esssup{p(x)∶x∈Ω}<.記p′(x)=p(x)/(p(x)-1). 令(Ω)為p(·)∈(Ω)并使得Hardy-Littlewood極大算子M滿足Lp(?)(Ω)有界的指數函數p(·)的集合.
在變指標Lp空間中有如下幾個重要的引理.
引理 1[4]設p(·)∈(n). 則存在常數C>0使得對所有n中的球B, 都有
引理 2[4]令p(·)∈(n). 則存在正常數C使得對所有n中的球B和所有可測子集S?B, 都有

其中δ1,δ2是常數且滿足0<δ1,δ2<1(注意在整篇文章中δ1, δ2都同引理2中的一樣).
引理3[1]令p(·)∈(n). 若f∈Lp(·)(n)且g∈Lp′(·)(n), 則fg在n上可積并且
其中rp=1+1/p--1/p+. 上述不等式被稱為廣義H?lder不等式.
下面我們給出變指標Herz空間的定義. 對于k∈, 令且Ak=BkBk-1. 記+和分別是所有正整數和所有非負整數的集合, 對k∈有χk=χAk, 若k∈+則且其中χAk是Ak的特征函數.
定義 1[4]令α∈, 0 在此基礎上我們給出變指標Herz型Hardy空間的定義及其原子分解特征. 用S(n)表示n上的Schwartz空間, 它是由無窮可微且在無窮遠處迅速遞減的函數所構成的,S′(n)表示S(n)的對偶空間. 令GNf(x)為f(x)的grand極大函數, 其定義為 定義2[6]令α∈, 0 對于x∈我們用[x]表示小于等于x的最大整數. 定義3[6]令nδ2≤α<,q(·)∈(n)且非負整數s≥[α-nδ2].n上的函數a被稱為中心(α,q(·))-原子, 如果它滿足:(i) 對某個r>0有suppa?;;(iii) 對任意滿足的多重指標β有∫a(x)xβdx=0.n上的函數a被稱為是限制型中心(α,q(·))-原子, 如果它滿足上述條件(ii), (iii)以及對某個r≥1有suppa?B(0,r). 引理 4[6]令nδ2≤α<, 0 其中下確界是對f的所有上述分解而取的. 設Sn-1為n(n≥2)上的單位球面,Ω∈Lipβ(Sn-1)(0<β≤1)是零次齊次函數且滿足∫Sn-1Ω(x′)dσ(x′)=0, 其中對任意x≠0有年Stein[8]定義了如下與Littlewood-Paleyg函數相關的Marcinkiewicz積分算子: 其中 近來,Cruz-Uribe等[9]給出了Marcinkiewicz積分算子的Lp(?)(n)有界性,下面將其推廣到變指標Herz型Hardy空間中. 定理1令Ω∈Lipβ(Sn-1)(0<β≤1/2),nδ2≤α 因此, 得 (1) 我們首先估計I1. 由aj的消失矩條件和廣義H?lder不等式, 得 C2-kn+(j-k)β‖aj‖Lq(·)(n)‖χBj‖Lq′(·)(n). 綜合J1,J2有 所以由引理1和引理2,有 ‖μ(aj)χk‖Lq(·)(n)≤C2-kn+(j-k)β‖aj‖Lq(·)(n)‖χBj‖Lq′(·)(n)‖χk‖Lq(·)(n)≤ (2) 因此, 當0 (3) 當1 (4) 現在我們來估計I2. 類似地,考慮p的兩種情形. 當0 (5) 當1 (6) 結合式(1)和式(3)~(6), 有 因此, 定理得證. 參考文獻: [1]KovácikO,RákosníkJ.OnspacesLp(x)andWk,p(x)[J].CzechoslovakMathJ, 1991, 41(4):592-618. [2]DieningL,HarjulehtoP,H?st?P,et al.LebesgueandSobolevspaceswithvariableexponents[M].Heidelberg:Springer, 2011. [3]XuJS.VariableBesovandTriebel-Lizorkinspaces[J].AnnAcadSciFennMath, 2008, 33: 511-522. [4]IzukiM.BoundednessofsublinearoperatorsonHerzspaceswithvariableexponentandapplicationtowaveletcharacterization[J].AnalMath, 2010, 36(1): 33-50. [5]NakaiE,SawanoY.HardyspaceswithvariableexponentsandgeneralizedCampanatospaces[J].JFunctAnal, 2012, 262(9):3 665-3 748. [6]WangHB,LiuZZ.TheHerz-typeHardyspaceswithvariableexponentandtheirapplications[J].TaiwaneseJMath, 2012, 16(4): 1 363-1 389. [7]HarjulehtoP,H?st?P,Lê úV, et al.Overviewofdifferentialequationswithnon-standardgrowth[J].NonlinearAnal, 2010, 72(12): 4 551-4 574. [8]SteinEM.OnthefunctionofLittlewood-Paley,LusinandMarcinkiewicz[J].TransAmerMathSoc, 1958, 88(2): 430-466. [9]Cruz-UribeD,SFO,FiorenzaA, et al.TheboundednessofclassicaloperatorsonvariableLpspaces[J]. Ann Acad Sci Fen Math, 2006, 31: 239-264. (編輯:郝秀清) MarcinkiewiczintegralsonHerz-typeHardyspaceswithvariableexponent WANGHong-bin (DepartmentofMathematicalandPhysicalScience,ZiboNormalCollege,Zibo255130,China) Abstract:Marcinkiewicz integrals are very important in harmonic analysis. The research on boundedness of Marcinkiewicz integrals has been one of important subjects in harmonic analysis. Using the boundedness of Marcinkiewicz integrals on variable Lebesgue spaces and the atomic decomposition characterizations of Herz-type Hardy spaces with variable exponent, we obtain the boundedness of Marcinkiewicz integrals on the homogeneous and non-homogeneous Herz-type Hardy spaces with variable exponent. Key words:Marcinkiewicz integral;variable exponent;Herz-type Hardy space;boundedness 中圖分類號:O174.2 文獻標志碼:A 文章編號:1672-6197(2015)04-0016-05 作者簡介:王洪彬, 男, hbwang2006@163.com 基金項目:國家自然科學基金資助項目(11171345);淄博師范高等專科學校研究課題(13xk023) 收稿日期:2014-12-04




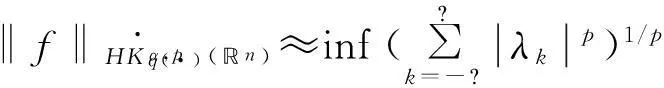
2 主要結論及證明