關于弧長概念的思考

彭娟　范周田　黃秋梅

摘要：在高等數學教材中，介紹弧微分定義是在給出曲線弧長定義之前，其中用到了曲線弧上兩點非常接近時弧長與弦長之比極限為這一結論，由于學生很難理解，本文提出了兩個解決方案。

關鍵詞：弧長；弦長；第一個重要極限

中圖分類號：G642.0 文獻標志碼：A 文章編號：1674-9324（2015）48-0244-02

度量問題是數學中一個非常古老的問題，而長度的度量是最常用的。有關長度的度量都以線段的長度定義為基礎，例如計算平面上一段曲線的弧長，最早也是最直接的方法是用一些直線段來作出和曲線相似的形狀，以直線段的長度代替曲線的弧長。僅憑直覺，關于曲線的弧長認識往往存在偏差，下面是一個典型的例子。

一、一個有趣的錯誤

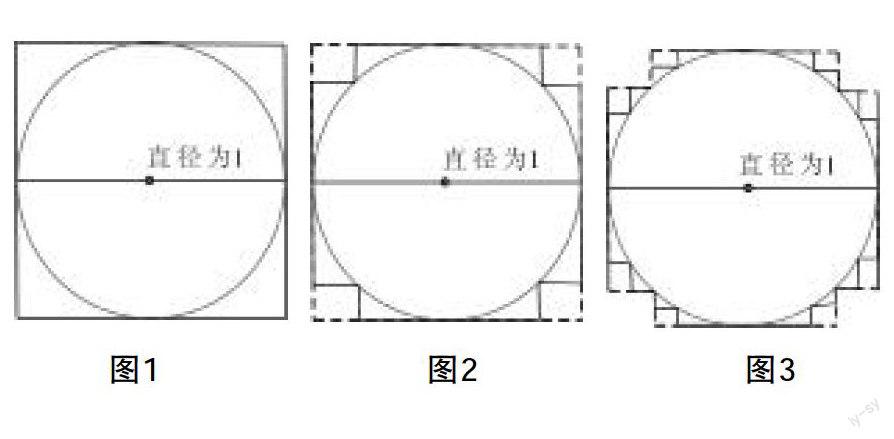
如圖1，有一個直徑為1的圓C，其長為L，在圓外作一個邊長為1的外切正方形C1，其長為4；然后將正方形的四個角向內折，使得直角的頂點接觸圓的邊（見圖2），這時曲線C2的長度仍為4；進一步將曲線C2的8個向外突出的直角內折，使直角的頂點接觸圓的邊（見圖3），形成的曲線C3長度仍不變。同法，每次將曲線Cn-1的向外突出的直角內折，使其直角的頂點接觸圓的邊，得到曲線Cn，其長度一直不變。隨著n的增大，曲線Cn越來越接近曲線C，所以曲線C的長度L=4，由此得到圓周率=圓周長/直徑=4。

上面的做法隱含了這樣一個假設：如果n趨于無窮時，曲線列Cn趨于曲線C，則曲線列Cn的長趨于曲線C的長。實際上，這個假設不成立。下面看一個反例。

二、有關弧微分和弧長定義的先后順序問題

在多數《高等數學》教材的內容安排上，都是先講授一元函數微分學，后講積分學。為了介紹曲率都先給出弧長的微分的定義。

這里試圖給出弧微分公式的推導，但其中用到的弧長與弦長之比趨于1這個暫時無法證明的結論，反而使得學生更難以理解，怎么解決大家的疑惑呢？有兩種處理方法。

方法一：給個具體實例。

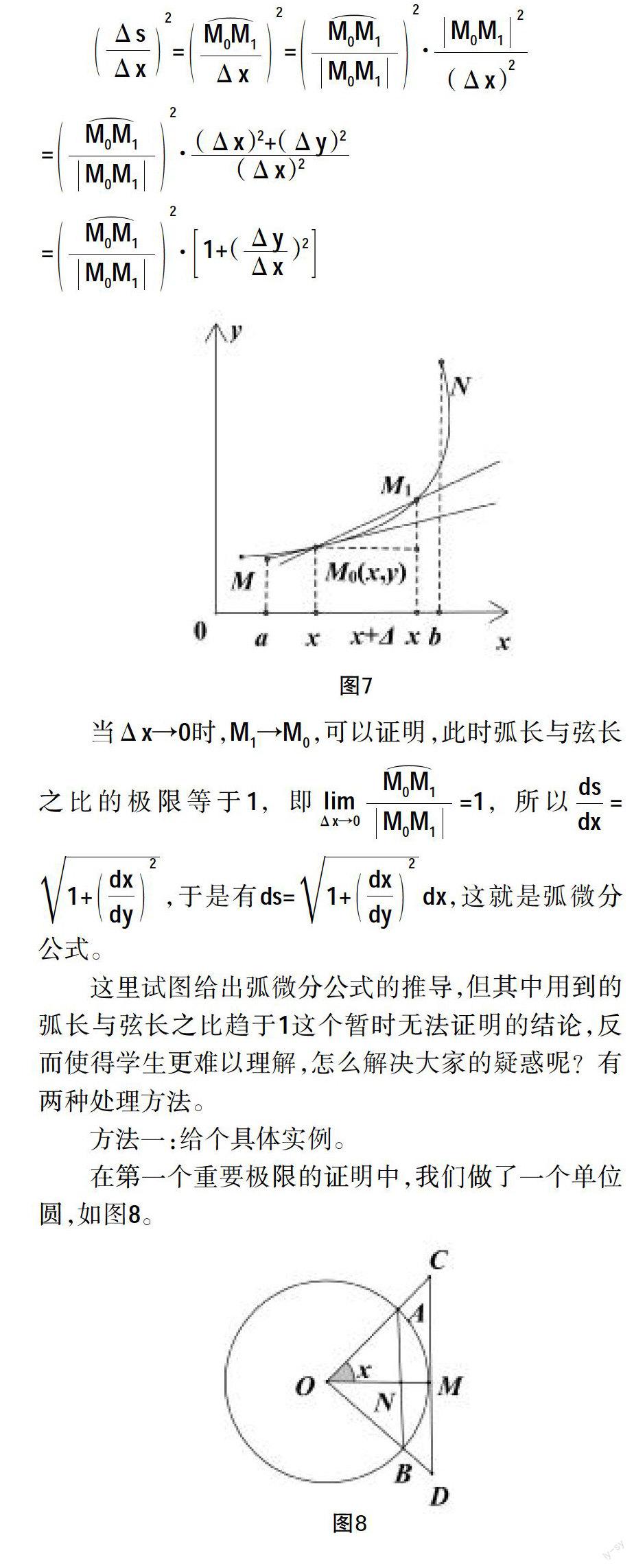
在第一個重要極限的證明中，我們做了一個單位圓，如圖8。

由此我們得到了圓周上兩點間距離很小時弧長與弦長之比極限等于1的結論，這是一個直觀的例子，這有助于學生的理解。

教師在介紹第一個重要極限時，往往只強調這個極限在推導正弦函數導數公式中的作用，從未從幾何上去分析它的實際意義，在教學過程中補充幾何意義，即說明了圓周上距離很小的兩點之間弧長與弦長之比極限等于1，這樣會提升學生的學習興趣。

方法二：先給出弧長的嚴格定義，再介紹弧微分。

弧長的定義默認了當曲線弧上兩點無限接近時，弧長與對應弦長之比極限等于1，有了這個結論再介紹弧微分的定義就不會有什么困難了。

弧長的定義也說明了第一部分中求圓的周長應該利用圓內接正多邊形的周長來逼近。

顯然，從邏輯上來說方法二是一個最嚴謹的做法，但是現有的高數教材都是先介紹弧微分，后來在介紹定積分的應用時才引入弧長的定義。這是因為曲率屬于導數知識的應用，討論曲率必須有弧微分的定義；而弧長的計算屬于定積分的應用，自然在后來才介紹。

我們以后講弧微分的定義時可以采用第一種方法，給個直觀的例子幫助學生理解就可以了。

參考文獻：

[1]范周田，張漢林.高等數學教程[M].北京：機械工業出版社，2011.