低噪聲風力機翼型設計方法及實驗分析

汪泉，陳進，程江濤，3，王君，孫金風，游穎

(1.湖北工業大學 機械工程學院，武漢430068;2.重慶大學 機械工程學院，重慶400030;3.丹麥技術大學 機械工程學院，靈比DK－2800)

風能是一種綠色可再生能源，取之不盡，用之不竭，隨著風力機的迅速發展與應用，風輪尺寸越來越大，運行過程中產生的噪聲也越來越嚴重，對周圍噪聲環境的影響也受到人們的廣泛關注.按照不同聲源風力機噪聲可分為機械噪聲和氣動噪聲.由于目前的機械制造水平及技術的不斷提高，機械噪聲可以較好的控制，而降低風力機的氣動噪聲成為目前研究的關鍵問題.風力機的氣動噪聲按照噪聲產生的機理可分為低頻噪聲、來流噪聲和翼型自身噪聲3種［1］.美國可再生能源實驗室的 Brooks等［2］在總結 NACA－0012 翼型噪聲風洞實驗的基礎上，提出了一種半經驗的風力機翼型噪聲計算模型(簡稱BPM模型).該模型計算速度和精度可滿足工程實際需求，是目前翼型噪聲計算使用最廣泛的方法之一.Zhu等［3］基于這種半經驗公式，引入動量葉素理論，考慮翼型的邊界層特性，提出了一種適用于風力機翼型的修正經驗模型，并與實驗結果對比從而驗證了該模型的準確性.司海青等［4］研究了數值預測風力機氣動噪聲的一種半經驗模型，并將計算結果與實驗數據進行了對比，從而驗證半經驗模型的有效性.余雷等［5］采用非線性計算氣動聲學方法和基于雷諾平均NS方程計算流體力學方法對常規后緣風力機翼型及其修型后的鈍后緣翼型的氣動噪聲進行了計算，并討論了這兩種計算方法不同的數值模擬能力.Singh等［6］針對小型風力機翼型，設計出了低雷諾數條件下的新型翼型，并將數值計算與風洞實驗進行了對比，揭示其流動機理.然而，以上研究均是對已有翼型進行噪聲特性研究，很少有對低噪聲翼型進行優化設計及噪聲實驗驗證;雖然風力機翼型的數值計算及實驗驗證的相關研究較多［7－13］，且研究成果顯著，但是缺乏相關的噪聲研究及實驗驗證.

因此，本文基于翼型泛函集成理論及翼型噪聲計算模型，將RFOIL與BPM模型耦合求解翼型噪聲特性;提出以升阻比與噪聲比值為設計目標函數，建立低噪聲風力機翼型優化數學模型，對優化后的新翼型進行氣動性能與噪聲實驗研究;為了驗證新翼型具有較低的噪聲特性，在相同的噪聲風洞實驗及風速條件下，與風力機常用NACA－64－618翼型進行噪聲對比分析并給出結果評價.

1 翼型噪聲計算模型

基于Brooks等［2］的計算模型(簡稱 BPM 模型)，翼型自身噪聲可分為:尾緣噪聲(TBL－TE)、葉尖噪聲(TIP)、失速噪聲(SEP)、鈍尾緣噪聲(TEB－VS)、層流渦噪聲(LBL－VS)［3，14］.而一般情況下，翼型自身的噪聲主要源于尾緣噪聲和失速噪聲，因此本文主要介紹這兩種噪聲計算公式.

1.1 湍流邊界層尾緣噪聲(TBL-TE)

當附著在葉片上的湍流邊界層流經尾緣與尾緣相互作用就會產生湍流邊界層尾緣噪聲.在一定的攻角和雷諾數下，在翼型表面的某個位置層流會發生轉捩變成湍流，而湍流會在尾緣的壓力面和吸力面產生波動的壓力，導致噪聲的產生.在攻角較小時，壓力面和吸力面的噪聲是主要的噪聲源［15］.

湍流邊界層尾緣噪聲SPL1是由湍流邊界層在壓力面產生的噪聲SPLp與在吸力面產生的噪聲SPLs之和［14］:

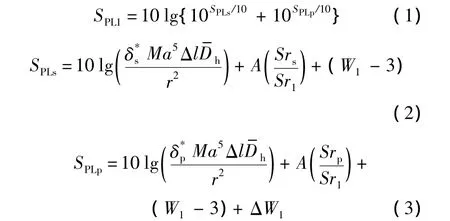
其中，尾緣噪聲表示成關于吸力面尾部邊界層相對厚度δ*s和壓力面尾部邊界層相對厚度δ*p的函數，與翼型的攻角α和來流的雷諾數Re有關;Ma為來流的馬赫數，是來流相對速度U與音速c0的比值;Sr為斯特勞哈爾數，Srs和Srp分別為吸力面和壓力面的斯特勞哈爾數，Sr1為尾緣噪聲的斯特勞哈爾基數;為高頻聲音方向函數;r為觀察者距離聲源距離;A為頻譜形狀函數;W1為振幅函數;ΔW1為聲壓級修正函數;Δl為翼型沿展向長度.

1.2 失速噪聲(SEP)

當攻角增大時，邊界層會發生分離，吸力面區域的湍渦會比低攻角時更大，當湍渦變成尾跡，進而產生分離流噪聲.隨著攻角增大到一定程度，邊界層發生大規模分離，翼型完全失速，此時失速噪聲為最主要噪聲:

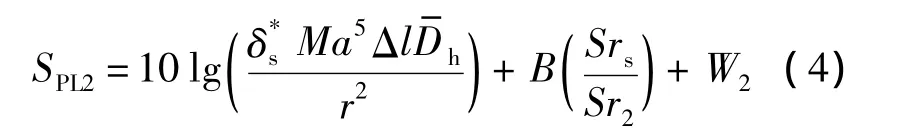
式中，B為頻譜形狀函數;W2為振幅函數.

2 翼型型線設計理論

基于翼型泛函集成理論［13］，翼型廓線在二維平面坐標方程可表示為

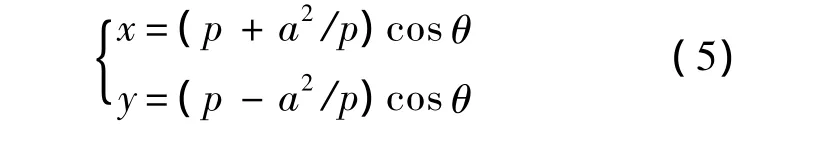
式中，a為0.25倍翼型的弦長;p為翼型的矢徑長度，可表示為

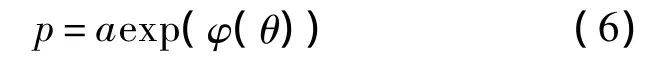
根據三角級數思想，翼型形函數可表示為

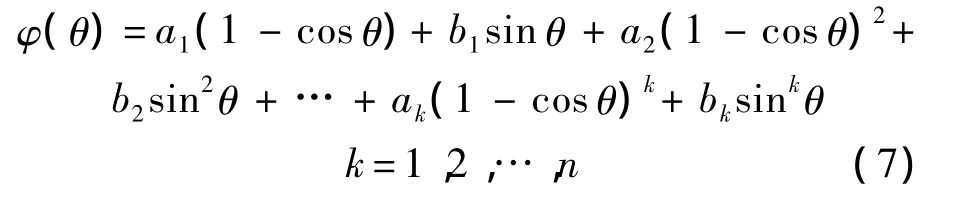
將式(6)、式(7)代入式(5)，選取不同的級數系數k，ak，bk，就可表示多種形狀的翼型.

3 低噪聲風力機翼型設計模型

隨著風力機的大型化，噪聲也越來越大，因此有必要設計低噪聲翼型，從而降低風力機的噪聲.翼型自身噪聲與一定雷諾數及攻角條件下翼型尾緣上下表面邊界層厚度密切相關，通過控制翼型表面邊界層厚度就可以控制翼型的噪聲.本文中翼型的邊界層參數通過RFOIL軟件計算，將翼型的參數方程與RFOIL耦合求解，在優化過程中計算翼型的氣動特性及壓力面和吸力面的邊界層厚度，從而控制翼型的氣動性能及噪聲值.

3.1 目標函數

翼型性能考慮的因素很多，除了低噪聲之外，還包括氣動、結構等不同學科的要求.本文主要考慮翼型具有較高的氣動性能及較低的噪聲大小，建立了以升阻比與噪聲值的比值為目標函數的數學模型:

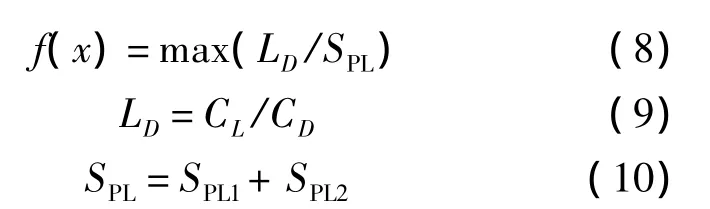
式中，CL為翼型的升力系數;CD為翼型的阻力系數;LD為翼型在設計攻角下的升阻比;SPL為翼型在設計攻角下的噪聲，這里設計攻角為6°.

3.2 設計變量和約束

對于翼型廓線的泛函集成方程，選擇式(7)的前6項系數為優化設計變量:

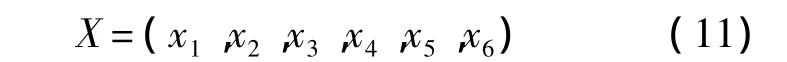
式中變量的變化空間根據翼型的形狀來確定，為了型線具有翼型的特征，對變量進行如下約束:

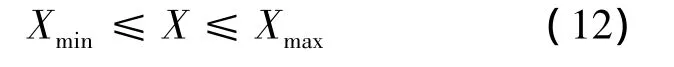
除了對形狀的要求以外，還得考慮翼型的結構兼容性問題.其中翼型的厚度及其所處的位置是結構兼容性兩個主要的參數，本文選取最大相對厚度為0.18的翼型進行優化設計，施加厚度及其位置約束為

其中，t為翼型的最大相對厚度;c為翼型的弦長.

3.3 優化結果

基于翼型泛函集成理論與噪聲計算模型，結合翼型優化模型，選取初始條件為:雷諾數Re=2.0×106，當地風速 V0=70 m/s，觀察者的距離r=1 m，觀察角度為90°，c=1 m，翼展長度為1 m，得到一種風力機新翼型CQU－DTU－B18，新翼型的輪廓型線如圖1所示.

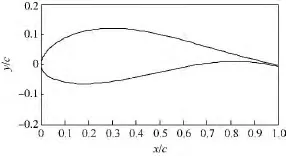
圖1 CQU－DTU－B18 翼型廓線Fig.1 CQU－DTU－B18 airfoil profile

4 實驗驗證

為了驗證翼型的氣動性能，聯合丹麥技術大學一起做了該新型翼型的風洞實驗，該實驗內容是在丹麥RISΦ實驗室完成的.翼型攻角范圍為－5°～20°，實驗雷諾數為 Re=2.0 ×106，馬赫數為0.15，實驗結果與RFOIL計算結果如圖2和圖3所示.

由圖2和圖3可知:實驗測試最大升力系數為1.777，出現在攻角為11°的位置，而RFOIL計算最大升力系數為1.919，出現在攻角為12°的位置，誤差較小為7.991%;實驗測試最大升阻比為142.3，出現在攻角為6°的位置，RFOIL計算最大升阻比為144.9，出現在攻角為7°的位置，誤差僅為1.833%，表明風洞實驗值與RFOIL計算結果吻合得較好.從而驗證了新翼型具有優良的氣動性能.

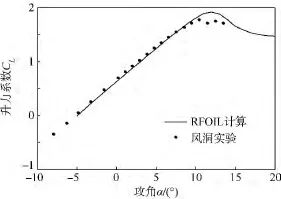
圖2 升力系數RFOIL計算與實驗結果的對比Fig.2 Comparison of the experimental results and the RFOIL predicted lift coefficient

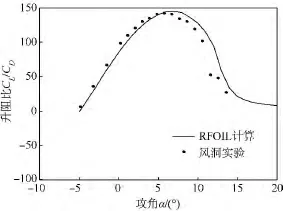
圖3 升阻比RFOIL計算與實驗結果的對比Fig.3 Comparison of experimental results and the RFOIL predicted lift/drag ratio

為了驗證新翼型具有較低的噪聲性能，下面重點研究新翼型噪聲特性，并將噪聲實驗結果與同等條件下常用翼型NACA－64－418翼型噪聲實驗結果進行對比分析.噪聲測試段及消音室如圖4所示，翼型噪聲實驗模型弦長為0.6 m，展向長度為1.62 m.觀察者距離翼型實驗段的距離為1.62 m，觀察角度為90°.該模型安裝有62個壓力孔，全部由鋁塊制造而成.噪聲原始數據由傳音器測試而來，并通過頻域波束形成技術進行處理.該技術能夠從背景噪聲中提取聲壓值.時間序列可以通過在32 s期間以51.2 kHz的采樣頻率進行測量，并分成200塊，8 192個樣本用以計算平均的交叉譜密度矩陣.考慮3種不同的風速工況，分別為30，45及60 m/s.由于這兩種翼型在0°攻角情況下的升力系數及失速攻角均有較大差別，因此很難比較他們的噪聲大小.而翼型的升力系數與升阻比是構建風力機葉片的主要性能，因此本文比較在相同升力系數情況下的噪聲特性.

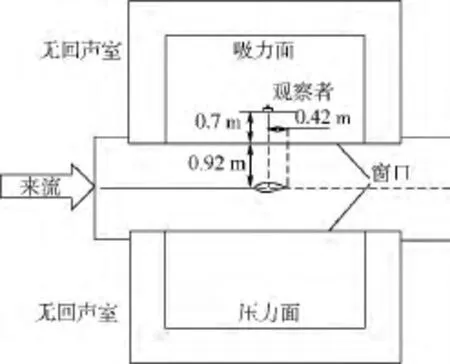
圖4 翼型噪聲測試示意圖Fig.4 Schematic of airfoil noise test section

圖5(a)和圖5(b)分別為風速為30 m/s，CL=0.52 和 CL=0.95 時 CQU－DTU－B18 翼型與NACA－64－618翼型的聲壓級對比圖.研究表明:相比 NACA－64－618 翼型，在頻率低于3 kHz時，新翼型具有較低的噪聲值;相比實驗數據，雖然翼型噪聲理論預測結果普遍偏大，但是總的趨勢是一致的.其主要原因是該理論是基于NACA0012翼型的一種半經驗計算模型，在某些參數的確定方面難免有些偏差.

為了研究風速對翼型噪聲特性的影響，分別對比分析風速在45 m/s和60 m/s時 CQU－DTUB18 翼型與 NACA－64－618 翼型的噪聲特性.圖5(c)和圖5(d)分別表示風速為45 m/s，CL=0.50 和 CL=0.94 時 CQU－DTU－B18 翼 型 與NACA－64－618翼型的聲壓級對比圖.由圖可知:相比 NACA－64－618 翼型，CQU－DTU－B18 翼型能夠產生更低的噪聲值;而且，相比風速為30 m/s時，當頻率大于600 Hz時理論預測結果與實驗值更加接近;當風速增加到60 m/s時，翼型噪聲隨頻率變化特性與風速為45 m/s時頗為相似，如圖5(e)和圖5(f)所示.

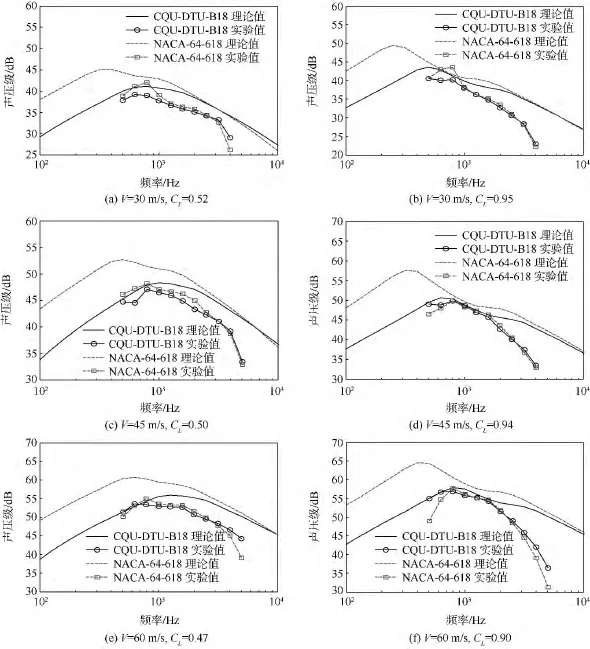
圖5 CQU－DTU－B18 與 NACA－64－618 翼型聲壓級對比圖Fig.5 Comparison of sound pressure level for CQU－DTU－B18 and NACA－64－618 airfoil

這兩種翼型總的噪聲大小對比如表1所示(風速為45 m/s).由表可知，在升力系數為0.50時，CQU－DTU－B18 翼型能夠產生比 NACA－64－618翼型低約2 dB的噪聲;在升力系數為0.94時，CQU－DTU－B18 翼型能夠產生比 NACA－64－618 翼型低約4 dB的噪聲.

表1 光滑條件下風速為45m/s時2種翼型的噪聲值對比Table1 Comparison of sound pressure level for the two airfoils in clean condition at a wind speed of 45 m/s dB

經過以上噪聲聲壓級及噪聲大小對比分析，可以得出:噪聲計算模型與實驗數據吻合得較好;相比 NACA－64－618 翼型，CQU－DTU－B18 翼型能夠產生更低的噪聲，從而研究了該翼型具有良好的低噪聲性能.

5 結論

1)基于翼型泛函集成理論及翼型噪聲計算模型，建立了低噪聲翼型優化設計數學模型，提出以翼型最大升阻比與噪聲比值為目標函數，采用RFOIL耦合BPM噪聲計算模型預測翼型噪聲值.優化設計得到一種低噪聲的新翼型.該方法較好地解決了翼型氣動性能與噪聲之間的矛盾，為設計低噪聲風力機翼型拓寬了思路.

2)為了驗證該翼型具有較低的噪聲特性，對CQU－DTU－B18 翼型及 NACA－64－618 翼型在相同的噪聲風洞實驗中進行了噪聲測試.實驗結果表明:相比 NACA－64－618 翼型，在相同的升力系數及風速條件下，CQU－DTU－B18翼型具有更低的噪聲大小;雖然基于BPM噪聲計算模型預測結果與實驗數據有一定的偏差，但是升壓級隨頻率的變化趨勢是一致的，從而驗證了該設計方法的可行性，同時對于翼型噪聲預測具有很好的指導作用.

References)

［1］ 賀德馨.風工程與工業空氣動力學［M］.北京:國防工業出版社，2006:221－225.He D X.Wind engineering and industrial aerodynamics［M］.Beijing:National Defense Industry Press，2006(in Chinese).

［2］ Brooks T F，Pope D S，Marcolini M A.Airfoil self－noise and prediction［M］.Washington:NASA，1989.

［3］ Zhu W J，Nicolai H，Shen W Z，et al.Modeling of aerodynamically generated noise from wind turbines［J］.Journal of Solar Energy Engineering，2005，127(4):517－528.

［4］ 司海青，王同光.風力機噪聲的預測方法研究［J］.空氣動力學學報，2011，29(6):801－804.Si H Q，Wang T G.Predicting method of aerodynamic noise from wind turbine［J］.Acta Aerodynamic Sinica，2011，29(6):801－804(in Chinese).

［5］ 余雷，宋文萍.風力機翼型氣動噪聲非線性聲學計算［J］.空氣動力學學報，2013，31(2):266－272.Yu L，Song W P.Aerodynamic noise prediction for wind turbine airfoils using non－linear acoustics solvers［J］.Acta Aerodynamic Sinica，2013，31(2):266－272(in Chinese).

［6］ Singh R K，Ahmed M R，Zullah M A，et al.Design of a low Reynolds number airfoil for small horizontal axis wind turbines［J］.Renewable Energy，2012，42:66－76.

［7］ Timmer W A，Van Tooij R P J O M.Summary of the Delft University wind turbine dedicated airfoils［J］.Journal of Solar Energy Engineering，2003，125(4):488－496.

［8］ Henriques J C C，Marques da Silva F，Estanqueiro A I，et al.Design of a new urban wind turbine airfoil using a preesure－load inverse method［J］.Renewable Energy，2009，34:2728－2734.

［9］ Ribeiro A F P，Awruch A M，Gomes H M.An airfoil optimization technique for wind turbines［J］.Applied Mathematical Modelling，2012，36(10):4898－4907.

［10］ 劉雄，羅文博，陳嚴，等.風力機翼型氣動噪聲優化設計研究［J］.機械工程學報，2011，47(14):134－139.Liu X，Luo W B，Chen Y，et al.Research on the aerodynamic noise optimization of wind turbine airfoil［J］.Journal of Mechanical Engineering，2011，47(14):134－139(in Chinese).

［11］ 周大高，柳陽威，文曉慶，等.改進SA模型對翼型分離流動的數值模擬［J］.北京航空航天大學學報，2012，38(10):1384－1388.Zhou D G，Liu Y W，Wen X Q，et al.Modification of SA model for predicting airfoil flow separation［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(10):1384－1388(in Chinese).

［12］ 黎作武，陳江，陳寶，等.風力機組葉片的先進翼型族設計［J］.空氣動力學學報，2012，30(10):130－136.Li Z W，Chen J，Chen B，et al.Design of advanced airfoil families for wind turbines［J］.Acta Aerodynamic Sinica，2012，30(1):130－136(in Chinese).

［13］ 王旭東，陳進，張石強.風力機葉片翼型型線集成設計理論研究［J］.中國機械工程，2009，20(2):211－213.Wang X D，Chen J，Zhang S Q.Integration study on airfoil profile for wind turbines［J］.China Mechanical Engineering，2009，20(2):211－213(in Chinese).

［14］ Zhu W J，S?rensen J N，Shen W Z.An aerodynamic noise propagation model for wind turbinesH［J］.Wind Engineering，2005，29(2):129－143.

［15］ Brooks T F，Marcolini M A.Scaling of airfoil self－noise using measured flow parameters［J］.AIAA Journal，1985，23(2):207－213.