不確定復雜網絡的廣義矩陣投影同步

鞏長忠，李飛燕

（中國民航大學理學院，天津300300）

0 引言

復雜網絡在自然界中普遍存在，例如，交通運輸網絡、萬維網（WWW）、生態網絡、新陳代謝網、人際關系網絡等等。因此，它在我們的日常生活中已經變得越來越重要。復雜網絡的本質就是復雜性，包括網絡的拓撲結構、動力學演化、節點多樣性等等。最近由于計算機的快速發展，我們能夠快速處理網絡中的大規模數據。隨著“小世界網絡”和“無標度網絡”［1－2］誕生，復雜網絡的研究已經成為一個熱點，吸引了許多科學和工程領域人士的關注。

在許多復雜動力學行為中，網絡同步是一個非常有意義的現象，已經成為復雜網絡研究的一個焦點。自從Pecora［3］提出并率先實現混沌同步以來，許多同步的方法（完全同步［4］、相同步［5］、滯后同步［6］、廣義同步［7］、投影同步［8－9］）先后被學者提出，投影同步是由Mainieri和Rehacek在研究部分線性混沌系統時首次提出的［10］。它由于其比例特性能夠使得混沌通信更加安全，所以廣義投影同步近年來得到廣泛的研究［11－13］。最近，文獻［14］研究了一類參數未知的超混沌系統的廣義函數投影滯后同步。文獻［15］研究了兩個不同的復雜網絡間的廣義矩陣投影滯后同步。網絡的節點可以有不同的動力學行為并且網絡維數也可以不同，研究結果不適用于參數不確定或者拓撲結構未知的復雜網絡。但現實的復雜網絡中存在著如節點的動力學系統含有未知參數或者網絡結構只是部分已知或者完全未知［16－18］。文獻［19］研究了帶有自適應雙尺度函數的不確定復雜網絡的自適應同步，并且未知的拓撲結構及未知參數可以識別，但沒有考慮時滯。在實際應用中復雜網絡節點間不僅存在t時刻的信息通信，而且也存在t－τ（t）時刻的信息通信［20－21］，即系統的演化趨勢不僅依賴于系統當前的狀態，也依賴于系統過去某一時刻的狀態。文獻［22］研究了復雜網絡的線性廣義同步。從以上研究成果中可以看出，在已有的大部分不確定復雜網絡的研究中，網絡模型維數都是相同的并且拓撲結構也相同，當網絡的拓撲結構不同或維數不相等時，以往的方法就受到了限制難以適用。例如同步將通過不同維數的振蕩器來實施，特別是生物科學和社會科學系統。

本文研究節點不恒等且維數不同的變時滯、不確定復雜網絡的廣義矩陣投影同步，它不僅僅使得不確定復雜的模型更加一般化，而且使得投影同步由一個常數或者對角矩陣演變為一個廣義矩陣，基于Lyapunov穩定性理論，利用自適應控制器得到了不確定復雜網絡廣義矩陣投影同步的判別準則，另外給出了一種響應網絡的構造方法，這種方法適應于幾乎所有的不確定復雜網絡。數值模擬結果驗證了方法的有效性和可行性。

1 網絡模型和預備知識

1.1 網絡模型

考慮一類含有N個非恒等節點，帶有時滯耦合的不確定復雜網絡：

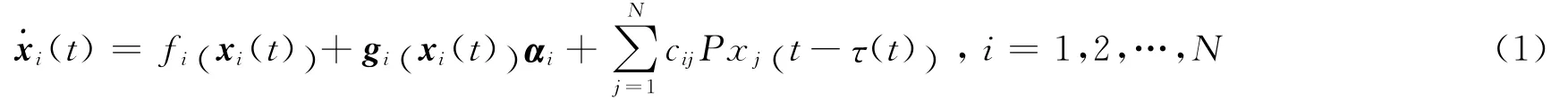
其中，xi（t）＝ （xi1，xi2，…，xin）T∈Rn是第i個節點的狀態變量；fi：Rn→Rn與gi：Rn→Rn×l是連續的非線性可微函數；τ（t）為節點間的時滯函數；αi∈Rl為l維未知參數；P∈Rn×n是內部耦合矩陣；C＝ （ciij）N×N∈RN×N是代表網絡耦合強度和拓撲結構的配置矩陣。矩陣C定義為：若第i個節點與第j個節點之間有連接（i≠j），則中每一行元素和為零，記方程 （1）為驅動網絡。

把含有非線性控制器的時滯耦合網絡記為響應網絡，其形式如式（2）：

其中，yi（t）＝ （yi1，yi2，…，yim）T∈Rm是第i個節點的狀態變量；Fi：Rm→Rm與Gi：Rm→Rm×r是連續的非線性可微函數；τ（t）為節點間的時滯函數；βi∈Rr為r維未知參數；ui（t）∈Rm是自適應控制器；Q∈Rm×m是內部耦合合矩陣；D＝ （diij）N×N∈RN×N是代表網絡的耦合強度和拓撲結構的配置矩陣，與矩陣C有相同的定義。

1.2 預備知識

定義1 設xi（t）是驅動網絡（1）中第i個節點的當前狀態變量，yi（t）是響應網絡（2）中第i個節點的當前狀態變量。對于xi（t），yi（t）如果存在一個常數矩陣M ∈Rm×n，并且 ‖M‖ ≠0，使得

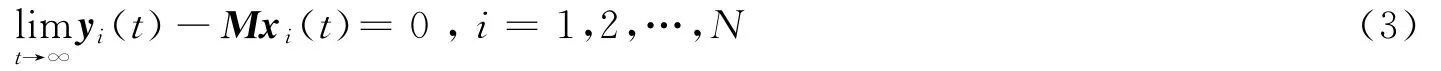
那么當τ（t）＞0時，網絡 （1），（2）達到廣義矩陣投影同步（GMPS）。

引理1 任給x，y∈Rn以及正定矩陣S，有2xTy≤xTSx＋yTS－1y 。假設1 存在非負常數l1，l2，使得對于任給定的x，y∈Rn有：

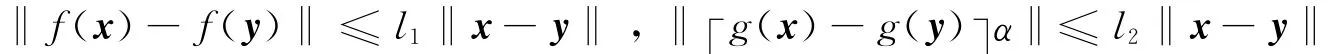
假設2 假設存在時滯函數τ（t）（＞0）是可微的，并且˙τ（t）≤η＜1，η是正常數。

2 同步準則

定義同步誤差：

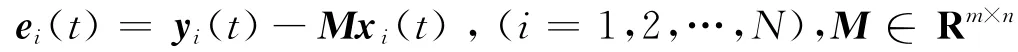
對時間t求導：

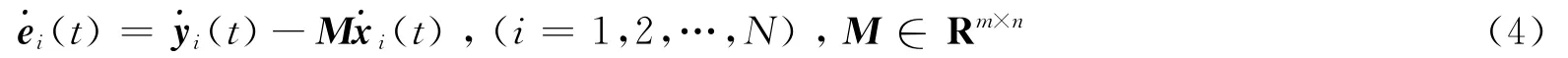
將方程 （1），（2）代入 （4）中，得到誤差的動力學系統為

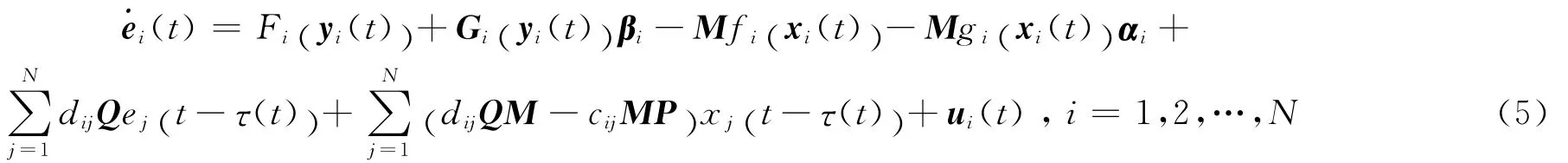
因此，當t→ ∞ ，ei（t）→0，網絡 （1），（2）實現了GMPS，則網絡 （1），（2）的廣義矩陣投影同步的實現就轉化為使誤差ei（t）零解的漸近穩定問題。

定理1 對于給定的廣義矩陣M ∈Rm×n（‖M‖≠0），在如下控制器和適應律作用下，網絡 （1），（2）實現了GMPS，并且未知的參數可以辨識，即

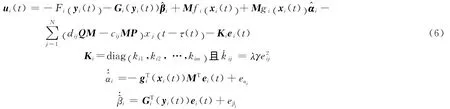
將（6）式代入（5）中，同步誤差動力學系統將被描述為

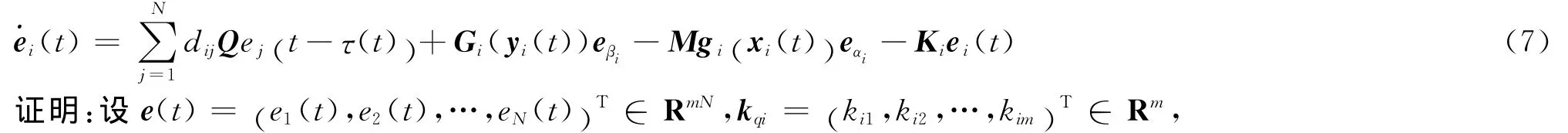
Iq＝ （1，1，…，1）∈Rm，I∈Rm×m是恒等矩陣。

構造李雅普諾夫函數：

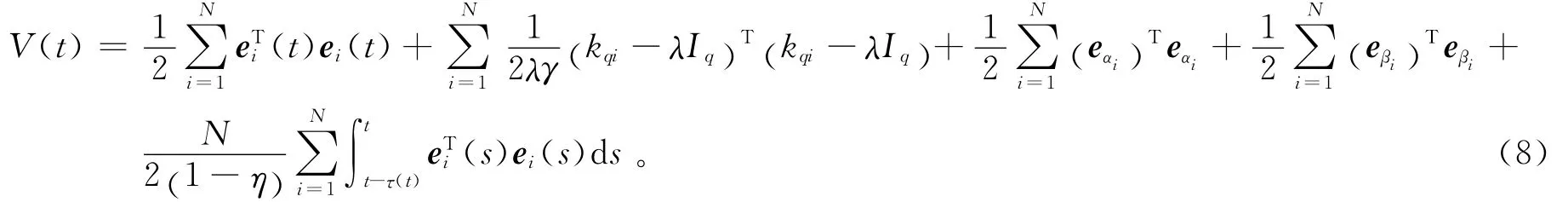
顯然V（t）≥0，即V（t）為正定函數，V（t）關于t求導：

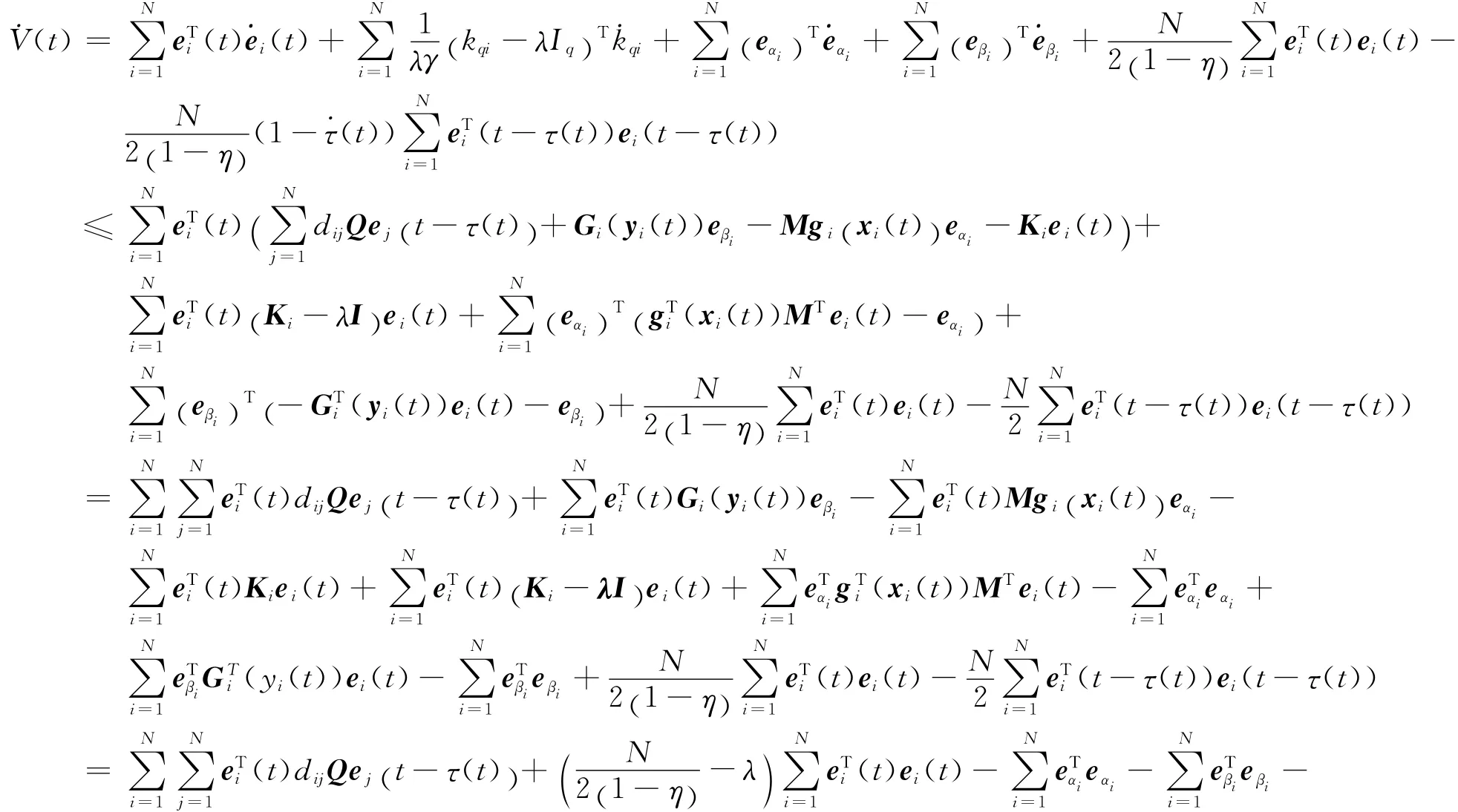
利用引理1，由于

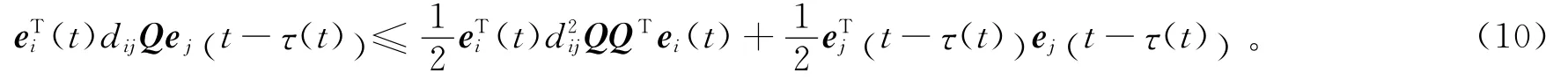
于是，將 （10）代入 （9）中

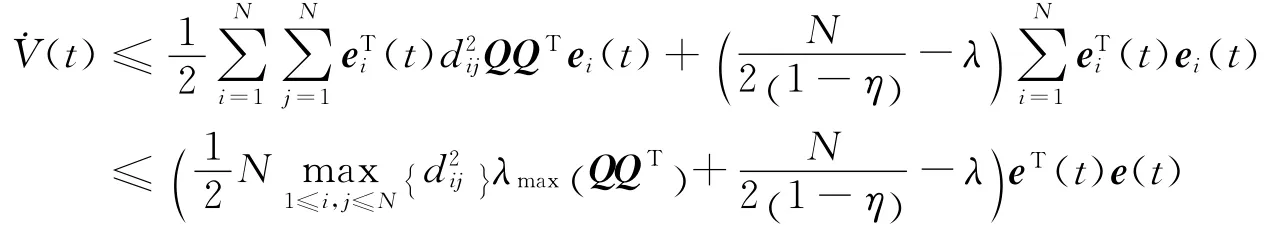
若令

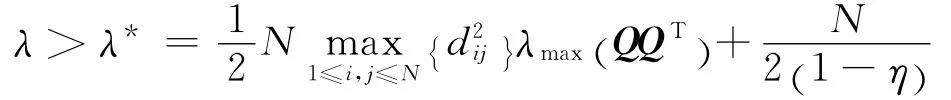
λmax（QQT）為矩陣ATA 的最大特征值，故（t）≤－eT（t）e（t），當（t）＝0時，ei（t）→0；當˙V（t）＜0時，由Lyapunov穩定性定理可得誤差ei（t）的零解是漸近穩定的，故網絡（1），（2）實現了GMPS。由定理1中的控制器和自適應律（6）可知未知參數可以辨識，即

如果MTM是可逆的，并且驅動網絡（1）中的耦合系數及節點參數都未知的情況下，構造如式（11）響應網絡，使其與未知的驅動網絡（1）對于給定的常值矩陣M實現GMPS。

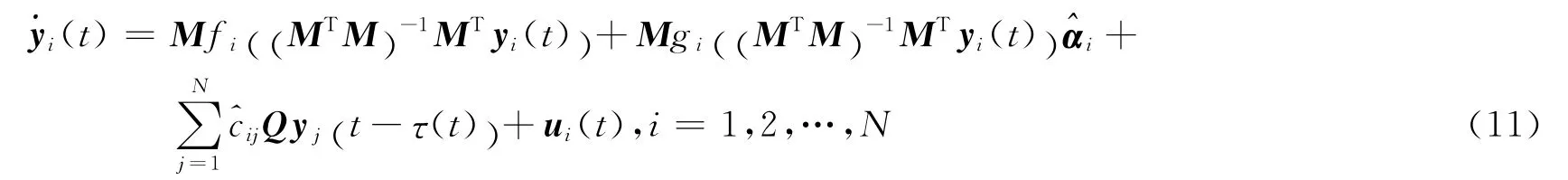
定義網絡 （1）和 （11）同步誤差：ei（t）＝yi（t）－Mxi（t），（i＝1，2…，N），M ∈Rm×n，對時間t求導，并將方程 （1），（11）代入得到誤差的動力學系統：

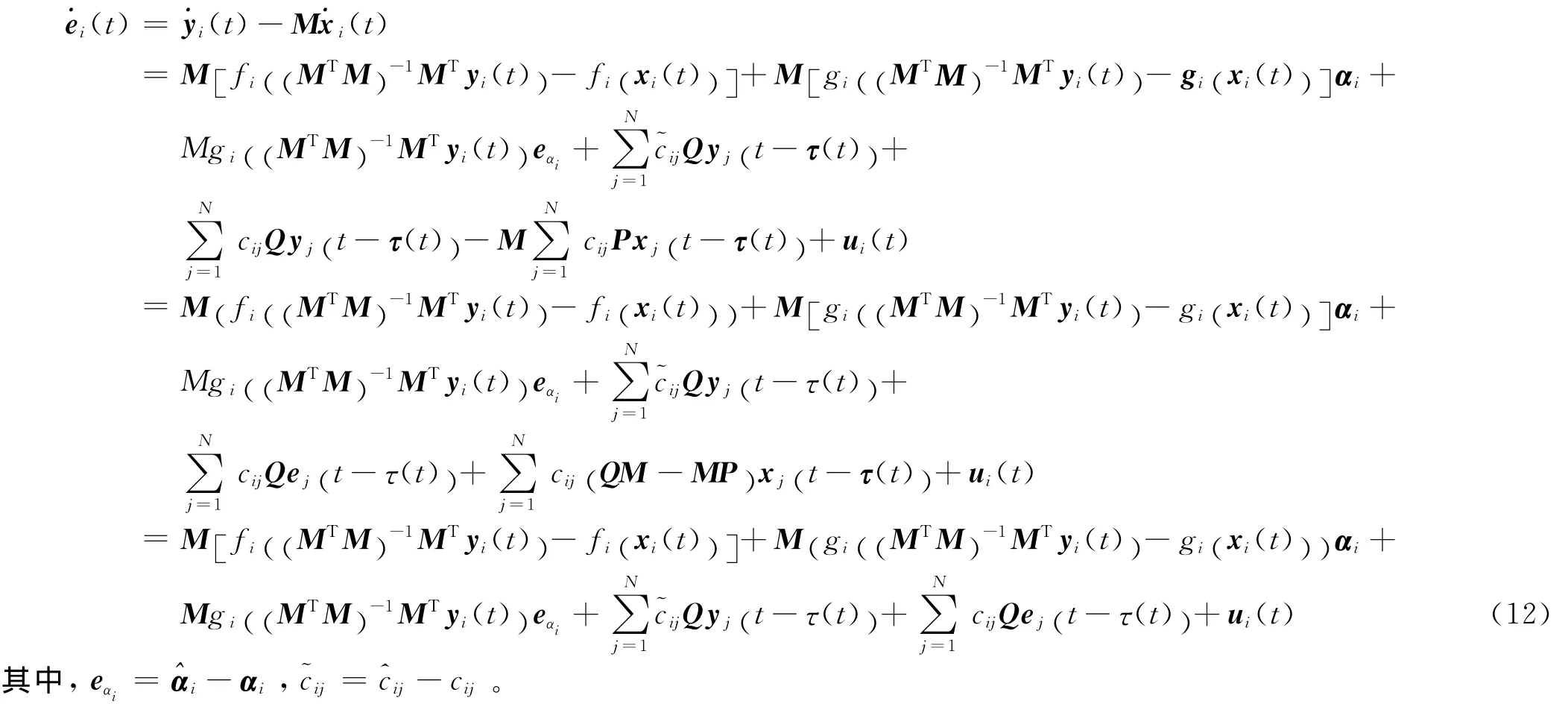
因此，若t→ ∞ 時，ei（t）→0，就說網絡 （1），（11）達到了廣義矩陣投影同步，即響應系統 （11）構造成立，于是（1），（11）的廣義矩陣投影同步的實現就轉化為使誤差ei（t）零解的漸近穩定問題。

定理2 在假設（1），（2）成立的情況下，對于給定的常數尺度矩陣M∈Rm×n（‖MTM‖≠0），在以下控制器和自適應律作用下，（1），（11）達到了廣義矩陣投影同步，并且未知的參數可以辨識。即

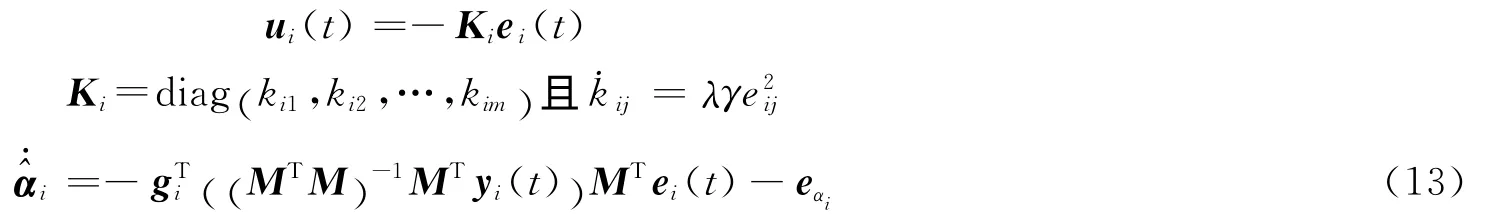
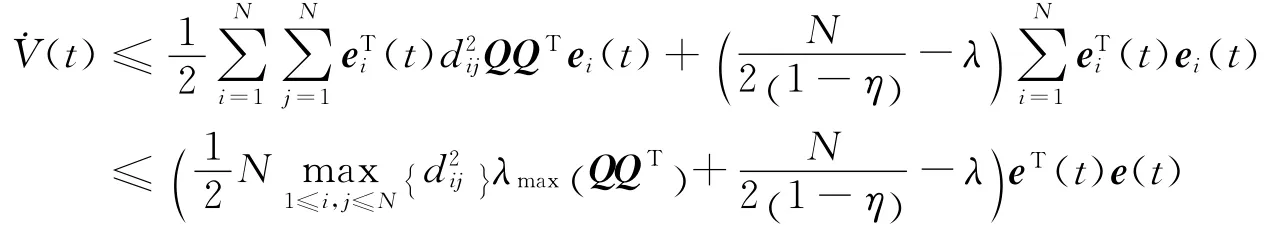
其中，i＝1，2，…N，j＝1，2，…，m 。

證明：考慮以下李雅普諾夫函數

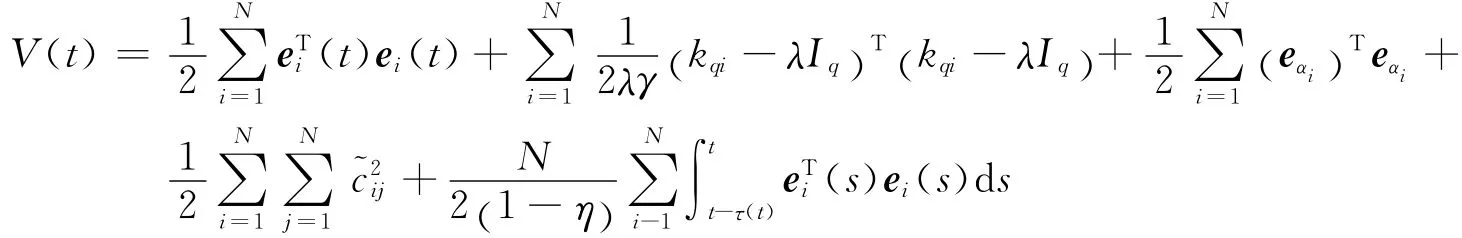
顯然V（t）≥0，即V（t）為正定函數，V（t）關于t求導：

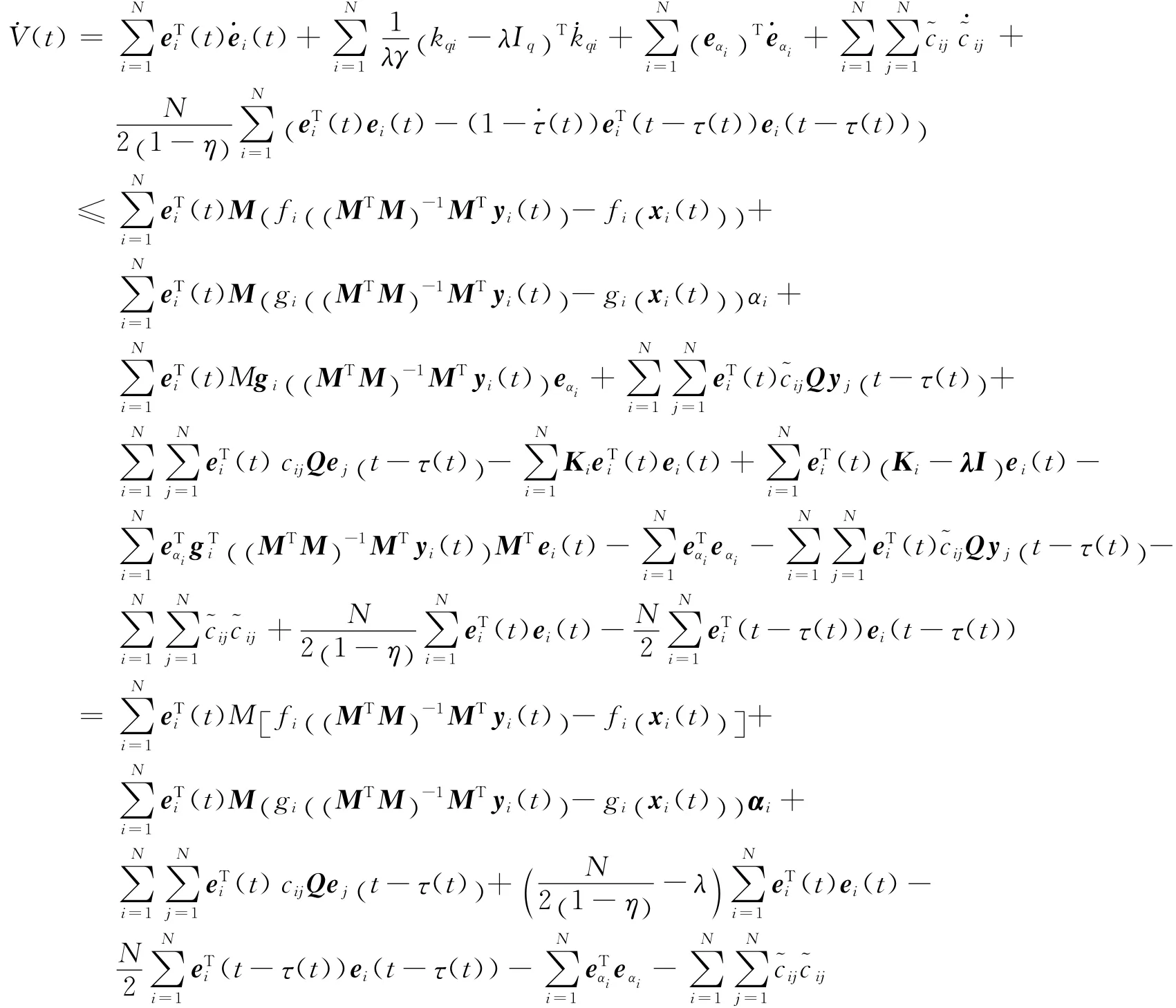
由假設（2）可知及引理（1）可知

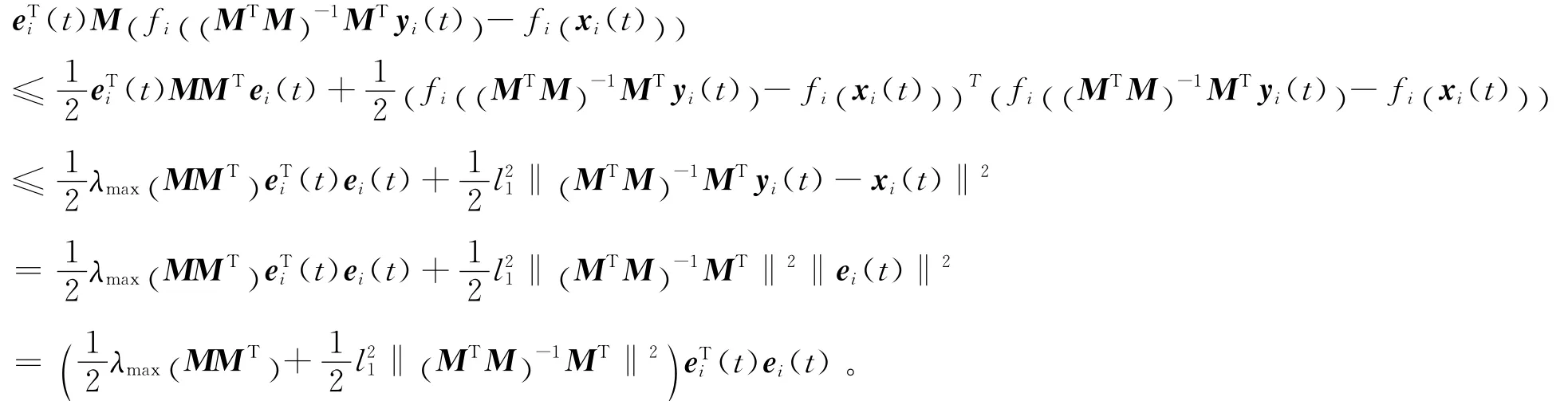
同理

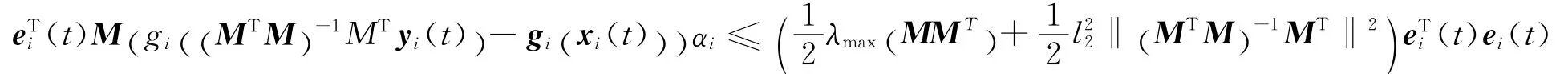
利用 （10）式得

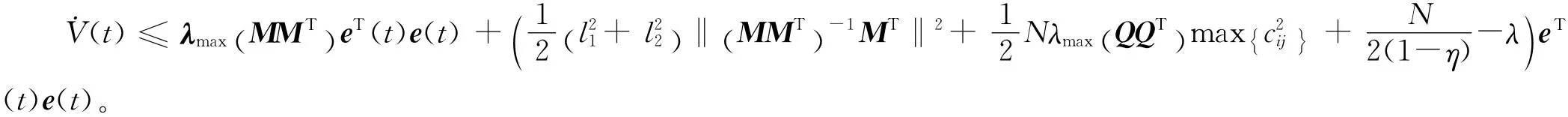
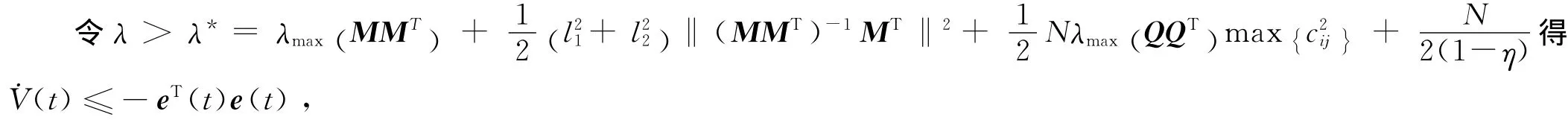
3 數值仿真

下面以Lorenz混沌系統和超混沌Lü系統為例，驗證理論的正確性和有效性。

選取N個不同的三維Lorenz混沌系統描述如式（14）：

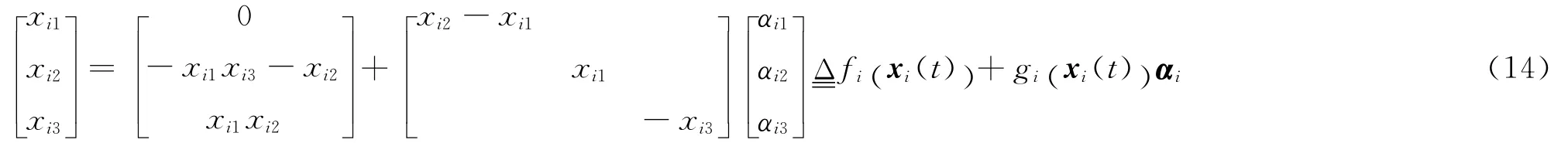
其中，xi1，xi2，xi3為第i個系統的狀態變量，αi1，αi2，αi3為系統的未知參數，當時，系統式（14）處于混沌狀態。

選取N個不同的四維超混沌Lü系統描述如式（15）：

其中，yi1，yi2，yi3，yi4為第i個系統的狀態變量，βi1，βi2，βi3，βi4為系統的未知參數。當βi1＝10，βi2＝5，βi3＝3，βi4＝0．5時，系統式（15）處于超混沌狀態。

為了仿真的方便，取含有5個節點的網絡進行仿真，由于網絡的配置矩陣是任意的，所以不妨取星形網絡和全局耦合網絡的配置矩陣C和D為

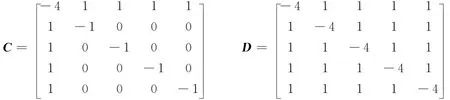
取系統內部耦合矩陣為恒等矩陣，即P∈I3×3，Q∈I4×4，時滯函數

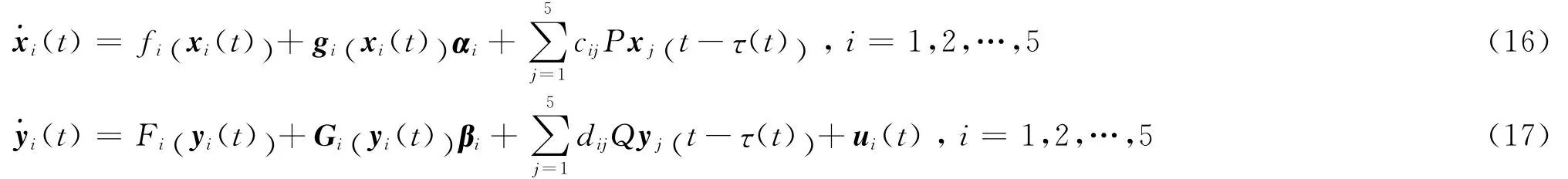
例1 使用（16）為驅動網絡，（17）為響應網絡，由定理1中證明過程可知λ＊≈42．8，取λ＝100，γ＝0．1，尺度，采用定理1中的控制器，未知參數估計值的初始值以及網絡（16），（17）的初始值在（0，1）之間任意取。

仿真結果如圖1所示，圖1給出了誤差曲線，可以得出復雜網絡（16），（17）在定理1控制器的作用下，趨于矩陣投影同步；圖2、圖3分別給出了參數αi，βi的估計，隨時間變化的曲線圖，可以看出網絡中所有的未知參數都收斂到真值。

圖1 誤差曲線Fig.1 The error curve

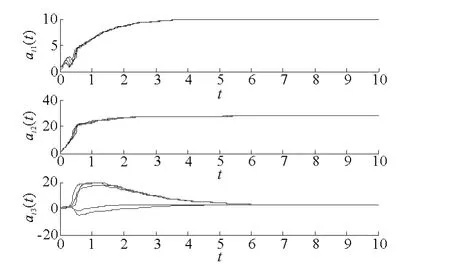
圖2 參數αi的估計Fig.2 The estimation ofαi

例2 使用（16）作為驅動網絡，參數αi與耦合矩陣C未知，構造式（18）網絡作為響應網絡

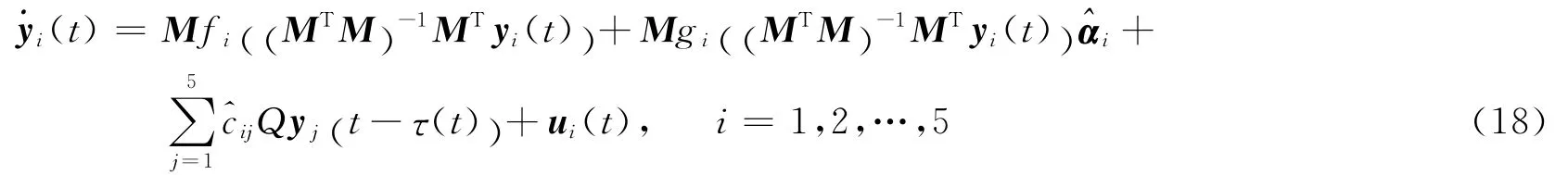
其中，

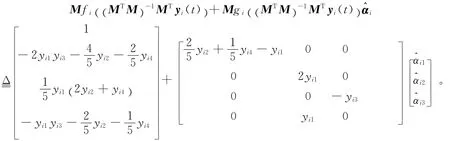
取Q∈I4×4，的初值在（0，1）之間任意取，常值矩陣M 及其余一切初值的取法同例1，采用定理2中的控制器，圖4給出了誤差曲線，可以看出（16），（18）在定理2中控制器的作用下趨于GMPS，圖5給出了參數αi的估計αi隨時間變化的曲線圖；圖6給出了網絡的拓撲結構cij的估計隨時間變化的曲線，可以看出網絡中所有的未知參數都收斂到真值。

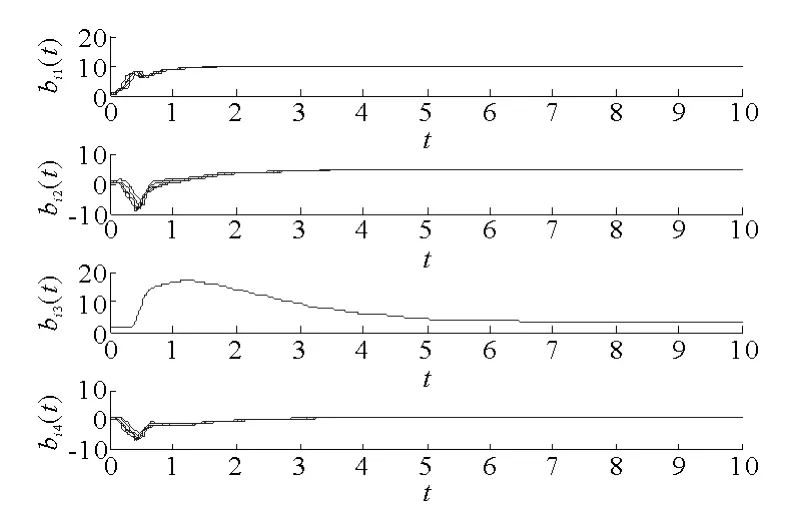
圖3 參數βi的估計Fig.3 The estimation ofβi

圖4 誤差曲線Fig.4 The error curve

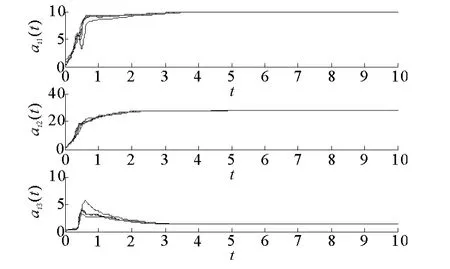
圖5 參數αi的估計Fig.5 The estimation ofαi

圖6 網絡的拓撲結構 的估計Fig.6 The estimated toloplogy

4 結語

本文采用自適應控制的方法研究了變時滯耦合的兩個不確定復雜網絡的廣義矩陣投影同步。每個網絡的維數不同、拓撲結構不恒等且節點帶有不同的動力學。一方面，基于Lyapunov穩定性理論，在節點參數未知的情況下，給出了不確定復雜網絡廣義矩陣投影同步的充分條件，參數可以識別；另一方面，當驅動網絡中的耦合系數也未知時，可以構造響應網絡，對于給定的廣義矩陣使其與驅動網絡達到投影同步，未知參數可以辨識，這不僅可以對該網絡進行同步控制達到預期效果，而且可以對參數進行辨識，確定網絡結構。最后數值仿真驗證了方法的有效性和可行性。現有與此類似的研究主要有如下兩個方面的工作：1）節點不恒等并且維數不同的復雜網絡自適應同步模型，其網絡耦合項無時滯且節點參數已知；2）復雜網絡的動力學節點含未知參數，而網絡的維數相同且耦合項為時滯而非變時滯的同步模型。該同步模型對結點含未知參數、耦合時滯且維數相同的復雜網絡同步的情況進行了推廣，具有更廣的適用范圍。

［1］ Watts D J，Stogatz S H.Collective dynamics of＇small－world＇networks［J］.Nature，1998，393（6684）：440－442.

［2］ Barabasi A L，Albert R .Emergence of Scaling in Random Networks［J］.Science，1998，286（5439）：509－520.

［3］ Pecora L M，Carroll T L.Synchronization in chaotic system ［J］.Physical Review Letters，1990，64（8）：821－824.

［4］ Agiza H N.Chaos synchronization of Lüdynamical system ［J］.Nonlinear Analysis，2004，58（1／2）：11－20.

［5］ Pikovsky A S，Rosenblum M G，Osipov G V.Phase synchronization of chaotic oscillators by external driving［J］.Physica D：Nonlinear Phenomena，1997，104（3／4）：219－238.

［6］ Li C D.Liao X F，Wong K W.Chaotic lag synchronization of coupled time－delayed systems and its applications in secure communication［J］.Physica D：Nonlinear Phenomen，2004，194（3／4）：187－202.

［7］ Rulkov N F.Sushchik M M，Tsimring L S，et al.Gneralized synchronization of chaos in directionally coupled chaotic systems［J］.Phys Rev E，1995，51（4）：980－994.

［8］ Yan J P，Li C P.Generalized projective synchronization of a unified chaotic system［J］.Chaos Solitons and Fractals，2005，26（4）：1119－1124.

［9］ Li G H.Modified projective synchronization of chaotic system ［J］.Chaos Solitons and Fractals，2007，32（5）：1786－1790.

［10］Mainieri R，Rehacek J.Projective synchronization in three－dimensional chaotic systems［J］.Physical Review letters，1999，82（15）：3042－3045.

［11］Li C P，Yan J P.Generalized projective synchronization of chaos：The cascade synchronization approach［J］.Chaos Solitons and Fractals，2006，30（1）：140－146.

［12］Li G H.Generalized projective synchronization of two chaotic systems by using active control［J］.Chaos Solitons and Fractals，2006，30（1）：77－82.

［13］Li Z G，Xu D L.Stability criterion for projective synchronization in three－dimensional chaotic systems［J］.Phys Letter A，2001，282（3）：175－179.

［14］柴秀麗，武相軍.一類參數未知超混沌系統的廣義函數投影滯后同步［J］.計算機應用，2013，33（3）：734－738.Cai Xiuli，Wu Xiangjun，Generalized function projective lag synchronization of a class of hyperchaotic systems with fully uncertain parameters［J］.Journal of Computer Applications，2013，33（3）：734－738.

［15］Dai H.Jia L X.Zhang Y B.Adaptive generalized matrix projective lag synchronization between two different complex networks with non－identical nodes and different dimensions［J］.Chin Phys B，2012，21（12）：141－152.

［16］Zhou J，Lu J A.Topology identification of weighted complex dynamical network［J］.Physica A，2007，386（1）：481－491.

［17］Li K，Lai C H，Adaptive－impulsive synchronization of uncertain complex dynamical networks［J］.Physics Letters A，2008，372（10）：1601－1606.

［18］Xu Y H，Zhou W N，Fang J A，et al.Topology identification and adaptive synchronization of uncertain complex networks with non－derivative and derivative coupling［J］.Journal of the Franklin Institute，2010，347（8）：1566－1576.

［19］Xu Y H.Zhou W N.Fang J A.Sun W.Topology identification and adaptive synchronization of uncertain complex networks with adaptive double scaling functions［J］.Common Nonlinear Sci Numer Simulat，2011，16（8）：3337－3343.

［20］Wu X J，Lu H.Generalized function projective（lag，anticipated and complete）synchronization between two different complex networks with nonidentical nodes［C］.Commun Nonlinear Sci Numer Simulat，2012，17（7）：3005－3021.

［21］李德奎，張建剛.時滯和非時滯耦合的驅動響應動態網絡的函數投影同步［J］.太原理工大學學報，2013，44（2）：162－167.Li Dekui，Zhang Jiangang.Function projection synchronization of drive－response dynamical networks with non－delayed and delayed coupling［J］.Journal of Taiyuan University of Technology，2013，44（2）：162－167.

［22］卞秋香，姚洪興.復雜網絡的線性廣義同步［J］.系統工程理論與實踐，2011，31（7）：1334－1340.Bain Qiuxiang，Yao Hongxing.Linear generalized synchronization of complex networks［J］.Systems Engineering－Theory and Practice，2011，31（7）：1334－1340.