戰斗力形態演化的分形模型

孫巨為，王志新，王小強

（陸航研究所，北京101121）

0 引言

分形理論是專門研究分形的幾何特征、數量表征及其規律和應用的科學，對于解決復雜系統問題非常有效。分維是分形理論中的最重要概念，它把分形客體的維數概念從整數擴展到了實數，實現了人類對維數概念認識的重大突破。戰斗力是一個典型的復雜系統，用分形理論對其加以研究，能夠在理論和實踐上解決許多懸而未決的難題，如戰斗中各種支離破碎的現象之間存在著某種有機的聯系等。

目前，運用復雜系統理論研究戰斗力已經成為軍事理論研究的熱點。文獻［1－3］界定了戰斗力、戰斗能力、戰斗潛力和戰斗效能之間的關系，即：戰斗力是戰斗能力在戰時表現出來的結果；戰斗能力是部隊遂行戰斗任務的基本能力；戰斗潛力是戰斗能力可能表現出來的最大值；戰斗效能是部隊發揮戰斗能力完成戰斗任務的程度。文獻［4－5］描述了物質化、能量化和信息化等戰斗力具體形態，構建了數字化部隊戰爭系統模型分解圖，將戰斗能力分解成部隊與武器、電子信息、決策指揮和后勤保障等能力。文獻［6－9］提出了戰斗力系統演化的開放性、非平衡性、非線性等自組織特征，從內在機制上闡釋了科學技術在戰斗力系統向有序演化過程中起第一作用（序參量）的機理，戰斗能力貢獻度和依賴度與戰斗體系結構演化涌現效應的聯系，以及演化后各種戰斗能力指標。這些觀點分別從不同角度描述了戰斗力形態的演化問題，盡管其中也有分形思維和思想，但都未對戰斗力形態演化的分形本質加以研究。文獻［10－11］等論述了城市人口和城市規模演化的分形特性，對于研究與之類似的戰斗力形態演化分形模型具有重要的參考價值。

本文以分形理論為背景，將戰斗力作為一個高度自治的復雜系統，論證其生成、保持、變化和衰減等分形模型，同時說明蘭徹斯特方程、奧西波夫方程和戰斗力指數模型的實質和來源，結合戰斗實例用定量方法探討戰斗力各要素相互作用的分形機理，進而提出戰斗力形態演化的分形思想。

1 戰斗力相關問題描述

戰斗力是戰斗力系統的簡稱，是指武裝力量遂行戰斗任務的能力，由人、武器裝備和人與武器裝備的結合等基本要素構成［12］，具體表現為各種戰斗力要素的綜合，包括突擊力、打擊力、保障（含信息、指揮、機動、防護、后裝保障）力等要素；戰斗效能是戰斗力量在戰斗進程中發揮有效作用的程度，也是反映和評價部隊戰斗力的尺度與標準［12］；戰斗力形態是指戰斗力結構、環境及其相互關系的總體；戰斗力形態演化是指戰斗力的結構、狀態、特性、行為和動能隨著戰斗進程的推移而發生的變化。

自治系統的功效是其主動通過與所在環境相互作用，實現自身目標，強調服從某些人或其它要素的控制，不能完全按照各要素自身的主觀意志行事。顯然，戰斗力既是一種有人參與的動力系統，也是一種典型的自治系統。按照一般系統論的觀點［13］，對于最簡單的戰斗力系統而言，戰斗力要素相關作用過程可用微分方程組（1）描述，即

其中，xi（i＝1，2，…，n） 為第i個要素；fi為xi變化時所有要素x1，x2，…，xn之間的相關作用算子，與指揮、行動和協同等方式有關；xi0為第i個要素的初值（常數），可理解為經過戰斗部署的戰斗力要素初始值，例如，遂行突擊、打擊或保障等任務的戰斗成員配置、狀態和數量等。

該方程組既說明了各要素之間相互關聯，互為因果，也說明了任何一個要素變化都以某種形式引起所有要素變化，從而導致戰斗力整體向前演化。例如，保障力增強后，可使打擊力也增強，而打擊力增強，可更好地壓制和毀傷威脅突擊行動的目標，這又使突擊力增強，打擊力和突擊力都增強后，就有利于大量殲敵，也能使保障成員和設備受到的威脅減少，進而使保障力得以保持和增強，打擊力、突擊力和保障力都增強后，整體戰斗力必然有一個躍升。

2 戰斗力生成分形模型

戰斗力生成是指在戰斗部署中各要素相互作用，使戰斗力從無到有、從小到大的過程。戰斗力生成的分形模型是用分形方法揭示戰斗力結構演化性的內在機理，描述情報搜集與分析、任務要求與區分、力量編組與配置、資源籌措與配送等對戰斗力生成的影響。由式（1），如果戰斗力只有兩個要素，則

其中，xi0和xj0分別為第i個和第j個要素的初值，均可認為趨近于0，即在戰斗部署前任何戰斗成員和武器裝備都不具備戰斗力，只有戰斗；ai和aj分別為第i個和第j個要素的生成系數，即戰斗部署合理性系數，戰斗部署越合理，該系數就越大，越容易生成戰斗力，反之亦然。

顯然，戰斗力形態具有非線性特征，對式（2）約簡，有［13］

式（3）反映了兩個要素之間的生成關系。當αij＞1時，第i個比第j個要素生成快；當αij＜1時，第i個比第j個要素生成慢；當αij＝1時，第i個與第j個要素同步生成。又由式（3），時刻t第i個和第j個要素的解為

將式（4）中時間項消元并化簡，得第i個和第j個要素的冪指數生成模型為

式（5）是一個廣義的分形模型。由于αij為第i個和第j個要素互為測度的結果，故αij具有分維性質，這里稱之為“互維數”。

由式（5），得時刻t所有要素的冪指數生成模型為

式（6）是對非線性戰斗力進行半線性分解的結果，簡化了內部關系，保持了主要的非線性特征，近似反映了第i個要素與其它要素的生成關系。

如果戰斗力包括n個要素xi（i＝1，2，…，n） ，則時刻t戰斗力的一般生成模型為

其中，g為各戰斗力要素的相互關系算子，該算子決定于指揮、行動和協同等方式。

對式（7）求全微分并做等價變換，得

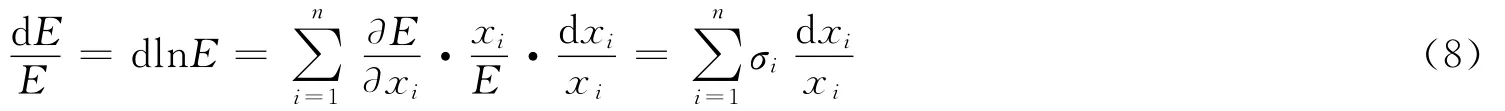
不難看出，σi＝?E／?xi·xi／E，為第i個要素與戰斗力的關聯系數，具有分維性質，分形維數為，且為常數，即認為式（8）是線性模型。對式（8）求積分得戰斗力的生成模型為

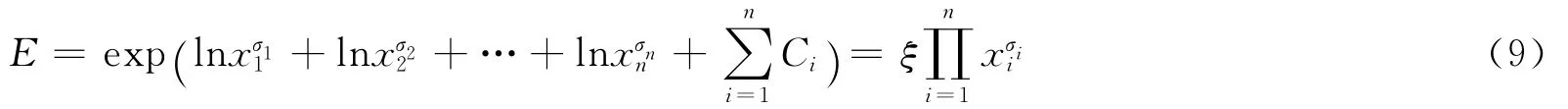
將式（5）代入到式（9）中，得戰斗力的生成模型為

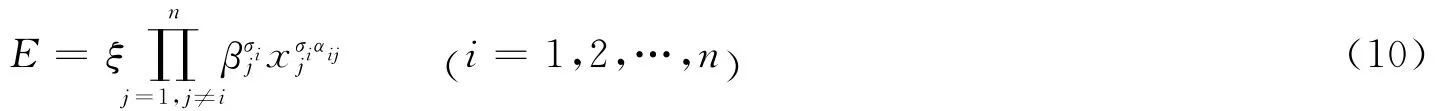
式（10）中，維數σi≠σj（i≠ j）為第i個要素發揮作用的程度，即靈敏度指數。該式說明戰斗力隨各要素的生成而生成，具有自仿射特征，并可化為任意多個xi的σi次冪的乘積形式。

3 戰斗力保持分形模型

戰斗力保持是指在戰斗實施中各要素逐步適應戰場情況，使戰斗力保持最大狀態的過程。其分形模型是用分形方法揭示戰斗力結構穩定性的內在機理，描述當前態勢與任務、力量配比與分配、戰法選擇與運用、時空協調與協同等對戰斗力保持的影響。由式（7）和式（9），在時刻t，有

式（11）說明戰斗力是一個k次齊次函數，即：如果所有要素都變化λ倍，則戰斗力同方向變化λk倍。特別是，當k＝1時，該戰斗力是線性齊次函數。例如，如果x1，x2，…，xn全部同時增加為λx1，λx2，…，λxn，則戰斗力E將增加為λkE，即：當λ＞1時，E遞增；當λ＝1時，E不變；當λ＜1時，E遞減。然而，如果要素數量n＞2且k為實數域的任意數值，則戰斗力與各要素之間不滿足線性關系。為此，用歐拉齊次函數定理確定式（11）中在λ＝1時的表達式，即

由式（12），當k＝1時，戰斗力最大值為

由式（9），如果各要素總量為X，則當k≠1且存在條件函數時，戰斗力最大值為

式（14）的拉格朗日函數為

其中，γ為拉格朗日參數。

由式（14）和式（15），用拉格朗日乘數法可求取戰斗力極值。存在極值條件的聯立方程組［14］為

求解聯立方程組得戰斗力有最大值的條件和解析解為

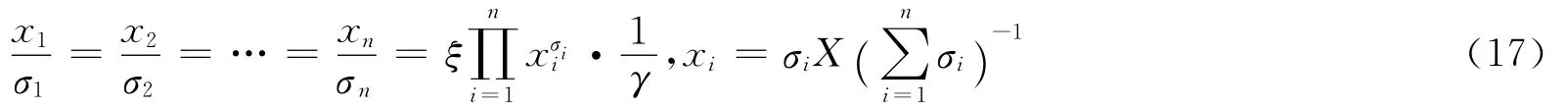
4 戰斗力變化分形模型

戰斗力變化是指在戰斗相持中因某個要素不能發揮作用，使戰斗力突然增大或減小的過程。其分形模型是用分形方法揭示戰斗力結構適應性的內在機理，描述敵我博弈與對抗、策略改變與調整、戰機創造與把握、環境利用與規避等對戰斗力變化的影響。這種現象是系統分形特性退化，有兩種模式，即：

第一，在時刻t某個要素變化與該要素大小無關，只取決于戰斗力的各種限制條件。

以第1個要素受到限制為例說明戰斗力變化現象。將式（18）代入式（9）得戰斗力的變化模型為

比較式（10）和式（19），可判別該模式下戰斗力變化方向，即

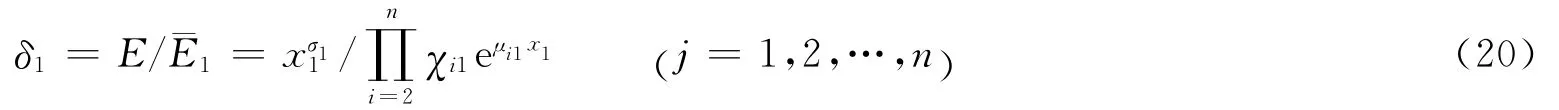
式（20）顯然有“指數函數的增大‘速度’比冪函數快得多”［14］，即戰斗相持到一定程度后，式（20）中任何一項δ1＜1。這說明指數函數模式的戰斗力大于冪函數模式，即由E向上變化為，原因是式（18）中，雖然第j個要素受到限制，但仍可使第i個要素以指數函數增大，使式（19）的戰斗力最終向增大方向變化。如，當兵力突擊受挫時，可通過增強火力打擊或綜合保障等提高整體戰斗力。

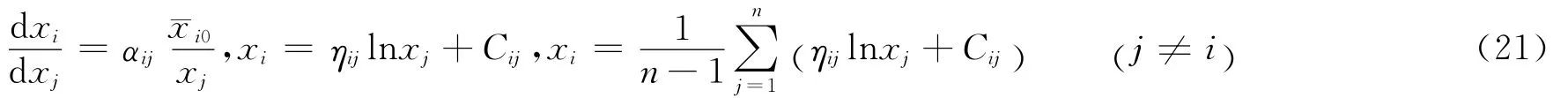
以第1個要素受到限制為例說明戰斗力變化現象。將式（21）代入式（9）得戰斗力變化模型為

比較式（22）和式（10），可判別該模式下戰斗力變化方向，即

式（23）顯然有“冪函數的增大‘速度’比對數函數快得多”［14］，即戰斗相持到一定程度后，式（23）中任何一項δ1＜1。這說明對數函數模式的戰斗力小于冪函數模式，即由E向下變化為，原因是式（21）中，雖然第i個要素受到限制，但第j個要素使其以對數函數減小，使式（19）的戰斗力最終向減小方向變化。如，當兵力突擊受挫時，未能有效組織與之協同的火力打擊或綜合保障等行動，兵力突擊效果將會進一步下降，導致整體戰斗力下降。

第二，時刻t兩個要素變化與這兩個要素的大小無關，只取決于戰斗力的各種限制條件。

其中，ζij＝αiji0／j0，為常數；Cij為積分常數。

以所有要素受到限制為例說明戰斗力變化現象。將式（24）代入（9）得戰斗力變化模型為

比較式（25）和式（10），可判別該模式下戰斗力的變化方向，即

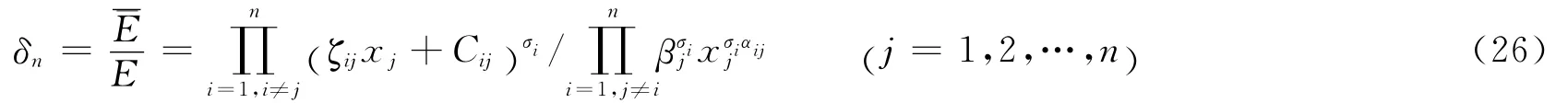
顯然，δn的增減方向可由必達法則判定，其值與ζij，Cij，σi，βj和αij等有關。

5 戰斗力衰減分形模型

戰斗力衰減是指在戰斗決勝中因某些條件不再具備，使戰斗力不斷消耗直至殆盡的過程。其分形模型是用分形方法揭示戰斗力結構脆弱性的內在機理，描述戰斗成員傷亡、武器彈藥消耗、指揮控制失效、戰場環境不利、戰斗精神崩潰等復雜因素對戰斗力衰減的影響。如果在時刻t第j個要素為（大于0的常數），第i個要素為（大于0的常數），并將之作為初值，則式（1）可表述為

由式（9），得戰斗力衰減模型為

6 戰斗力分形模型特例

長期以來，許多學者對戰斗力形態演化問題進行過研究，并給出了各種比較實用的演化模型［15－16］。從結構特點上看，這些模型都是戰斗力形態演化分形模型的一種特例或派生形式。主要有：

2）奧西波夫戰斗方程。由式（29），當i＝1，σ1＝1.5，其他參數含義和取值不變時，有，該結果與奧西波夫方程中A，B方戰斗效能等價，即“A方損失＝K·（B方實力）p”和“B方損失＝K·（A方實力）p”。其中，K為比例系數；p為憑經驗確定的指數。

上述特例說明，戰斗力形態演化分形模型不只是一種抽象的理論模型，還是一種能夠指導戰斗實踐的可派生模型，根據戰斗需要和相關數據，可以派生出不同結構和精度的模型。

7 戰斗力分形模型應用

分析式（9）、（14）、（22）、（25）和（29）不難發現，各戰斗階段戰斗力形態具有很強的“伸縮性”，當只考慮某要素與整體的關系時，其余要素信息均“壓縮”在了系數或參數當中。

7.1 戰斗力測度關系模型

為了將上述戰斗力模型解析為具體的測度關系模型，并利用其中的自仿射性質，變量選擇應遵循可觀測、能甄別、有代表性的原則。為此，可將戰斗效能（用敵方傷亡戰斗成員數表征）作為戰斗力的輸出變量，將戰斗實力（包括突擊實力、打擊實力和保障實力，用我方相應的戰斗成員數表征）作為戰斗力的輸入變量，由此可建立如下戰斗力各要素實力和戰斗效能之間的數理關系。

突擊實力與打擊實力、打擊實力與保障實力、保障實力與突擊實力之間異速生長關系為

其中，xt，xd和xz分別為突擊實力、打擊實力和保障實力，戰斗實力X0＝xt＋xd＋xz。

基于戰斗實力、突擊實力、打擊實力和保障實力等單項的戰斗效能彈性模型為

基于突擊實力、打擊實力和保障實力等綜合的戰斗效能彈性模型為

其中，adt，azd，atz，bdt，bzd，btz，C0，Ct，Cd，Cz，δ0，δt，δd，δz，η，ht，hd，hz均為參數，不難得到，hd＝δd／3，hz＝δz／3。

假定相應于xt，xd，xz和Ex的廣義維數分別為Dxt，Dxd，Dxz和DEx，由幾何測度關系知

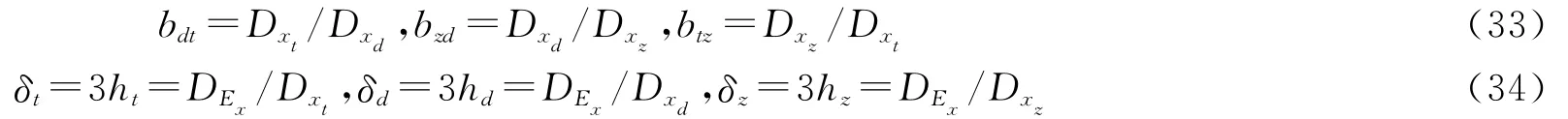
由式（33）和（34）可得

因此，只要bdt，bzd和btz不是整數或整數之比，δt，δd，δz，ht，hd和hz就具有分維性質。

7.2 戰斗力測度關系實例

現以我軍歷史上某次陸軍戰役中陸軍第×師進攻戰斗為例，說明戰斗力各要素的測度關系。該師戰斗目的是殲滅當前守敵一個團大部，為友鄰實施戰役縱深戰斗創造條件。該師已完成戰斗部署，于19××年×月×日拂曉用火力準備的方式觸發戰斗，包括火力準備、前沿突擊、抗反沖擊、分割圍殲、縱深戰斗、追擊殘敵、清剿戰場等階段。根據戰斗日志，該師戰斗共進行8晝夜，每個戰斗日敵我戰斗實力變化如表1所示（注：表中假設情況供輔助分析）。

將表1中點列數據 （X0（t），Ex（t） ） 、（xt（t），Ex（t） ） 、（xd（t），Ex（t） ） 和 （xz（t），Ex（t） ） 分別標繪于對數坐標圖中，其分布呈對數線性分布趨勢，如圖1～圖4所示。將表1中點列數據 （X′0（t），Ex（t） ） 繪于對數坐標圖中，其分布呈對數線性分布趨勢相對較差，如圖5所示。

可根據式（30）和（31）的雙對數形式和表1數據，利用最小二乘法計算有關參數。這樣，基于戰斗力、突擊力、打擊力和保障力等單項的戰斗效能動力相似模型為

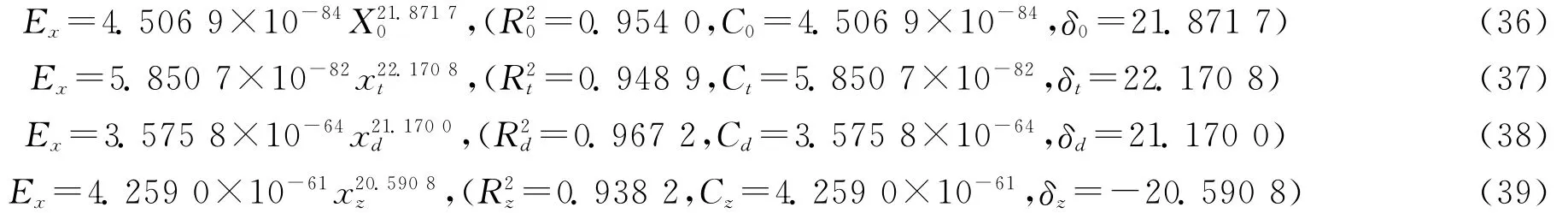
突擊力與打擊力、打擊力與保障力、保障力與突擊力的異速生長關系分別為

表1 陸軍第×師進攻戰斗各戰斗日敵我雙方戰斗力相關數據統計Tab.1 The related date statistics of a attack battle of the army′s division

圖1 戰斗實力與戰斗效能對數關系（實際情況）Fig.1 Logarithmic relationship between combat power combat effectiveness（Actual situation）

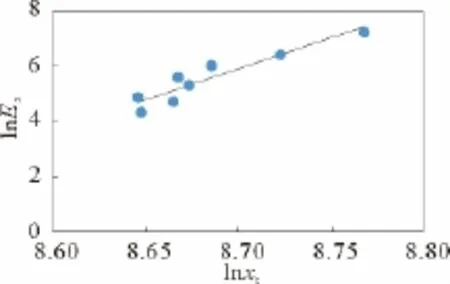
圖2 突擊實力與戰斗效能對數關系（實際情況）Fig.2 Logarithmic relationship between assault power and combat effectivenss（Actual situation）

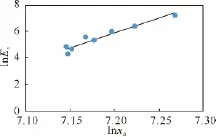
圖3 打擊實力與戰斗效能對數關系（實際情況）Fig.3 Logarithmic relationship between force power and combat effectiveness（Actual situation）

圖4 保障實力與戰斗效能對數關系（實際情況）Fig.4 Logarithmic relationship between support power and combat effectiveness（Actual situation）

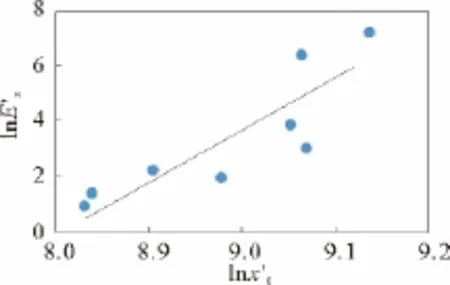
圖5 戰斗實力與戰斗效能對數關系（假設情況）Fig.5 Logarithmic relationship between combat power and combat effectiveness（Hypothetical situation）

由式（32）可計算得η＝4.466 5×10－69，ht＝7.390 2，hd＝7.056 7，hz＝6.863 6。這樣，基于突擊力、打擊力和保障力等綜合的戰斗效能彈性模型為

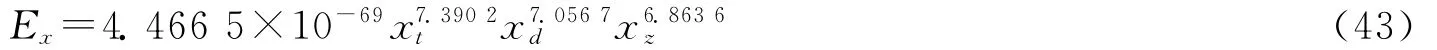
由表1實際情況數據和理論模型知：bdt＝1.051 6，δt＝22.170 8，δd＝21.170 0，δt／δd＝1.047 3，ht／hd＝7.390 2／7.056 7＝1.047 3，滿足式（35）。將表1中xt、xd和xz數據代入式（37）、（38）和（39）中，計算結果與表1中相應的Ex值基本一致，聯系到雙對數坐標圖的點列分布狀態（圖1～4），可認為該師戰斗力形態演化具有自仿射的分形結構。而且，ht，hd和hz具體數值均為非整數或整數之比，系統是分數維的。

根據表1假設情況數據和最小二乘法，可計算得戰斗實力與戰斗效能的動力相似模型為

顯然，由式（36）～式（44）可知，相關指數R′20?R20，說明戰斗力分形特性出現了退化，表現為第3～第8個戰斗日傷亡較大，其原因一般是情報不準、決策失誤、執行不力、敵人善戰等，其本質是戰斗力各要素大小及其關系發生了變化，使預期戰斗力分形結構遭到破壞。又可知，變量指數或維數δ′0?δ0，說明兩種情況的戰斗力系統結構不一樣。根據分形理論，維數越大，系統結構就越復雜，系統運行效率也越大，但對系統結構可靠性提出了較高要求，因為系統結構一旦破壞就很難恢復。因此，制定戰斗方案時應考慮多種情況協同，強化戰斗預備隊和臨機決策的作用等。

8 結語

戰斗力形態演化的分形特性是大自然分形特性的具體表現，是戰斗力固有的基本性質。對于預期的戰斗力，戰斗力形態演化的分形模型可表述成戰斗力各要素相關的冪指數函數形式，具有自仿射特征。只有保持生成系數比與相應戰斗力構成要素的比值恒定，才能使戰斗力最大。如果外部和內部條件不能滿足有關要求，則戰斗力形態演化將會發生重大變化，即戰斗力突然增大或減小，這往往意味著戰機將要出現。因此，運用分形理論研究戰斗力，不僅有助于揭示戰斗力的本質和規律，闡釋克敵制勝的機理和方法，而且還可使戰斗方案和戰斗組織更加合理，針對破壞戰斗力分形結構的因素進行分析，從而創造和把握戰機，為化解戰場危機、探索制勝機理提供依據。

［1］ 胡曉峰，楊鏡宇，司光亞，等.戰爭復雜系統仿真分析與實驗［M］.北京：國防大學大學出版社，2008：279－384.

［2］ 胡曉峰，司光亞，吳琳，等.戰爭模擬引論（上）［M］.北京：國防大學大學出版社，2004：191－199.

［3］ 胡曉峰，羅批，司光亞，等.戰爭復雜系統建模與仿真［M］.北京：國防大學大學出版社，2005：385－391.

［4］ 劉西山.戰斗力本質論［D］.江蘇：南京陸軍指揮學院，2008.Liu Xishan.The essence of fighting capacity［D］.Jiangsu：Nan Jing Army Command College，2008.

［5］ 胡軍，李濤，李亮，等.數字化部隊作戰能力評估指標體系［J］.火力與指揮控制，2009，34（9）：76－83.Hu Jun，Li Tao，Li Liang，et al.Research on combat capability evaluation guideline system of digitization troop［J］.Fire Control and Command Control，2009，34（9）：76－83.

［6］ 宋黎.戰斗力系統自組織演化分析［J］.南京政治學院學報，2005（6）：45－50.Song Li.Analysis on the self－organized evolution of combat capability systems［J］.Journal of PLA Nanjing Institute of Politics，2005（6）：45－50.

［7］ 宋黎.科學技術第一戰斗力的系統分析及實現途徑［D］.遼寧：大連理工大學，2007.Song Li.Analysis and approach of system of science and technology of the first combat［D］.Liaoning：Dalian University of Technology，2007.

［8］ 夏璐，邢清華，范海雄，等.基于能力關系的作戰體系結構演化涌現效應［J］.火力與指揮控制，2013，38（7）：42－45，49.Xia Lu，Xing Qinghua，Fan Haixiong，et al.Research on emergence effect in evolution of operational system－of－systems architecture based on capability relationship［J］.Fire Control ＆Command Control，2013，38（7）：42－45，49.

［9］ 溫睿，馬亞萍，王崢，等.一種作戰體系動態演化模型［J］.系統仿真學報，2011（7）：85－92.Wen Rui，Ma Yaping，Wang Zheng，et al.Dynamic evolution model of a combat system［J］.Journal of System Simulation，2011（7）：85－92.

［10］De Kcersmaecker M－L，Frankhauser P，Thomas I.Using fractal dimensions for characterizing intra－urban diversity：the example of Brussels［J］.Geographical Analysis，2003，35（4）：310－328.

［11］Benguigui L，Czamanski D，Marinov M，et al.When and where is a city fractal？［J］.Environment and Planning：Planning and Design，2000，27（4）：507－519.

［12］全軍軍事術語委員會，軍事科學院.中國人民解放軍軍語［Z］.北京：軍事科學出版社，2011：10.

［13］馮·貝塔朗菲著.一般系統論的基礎、發展和應用［M］.林康義，魏宏森，譯.北京：清華大學出版社，1987：52－55.

［14］同濟大學數學系.高等數學（第六版上冊）［M］.北京：高等教育出版社，2007：137.

［15］王輝青.中國軍事百科全書（第二冊）軍事運籌（學科分冊）［M］.北京：中國大百科全書出版社，2007：45－99.

［16］凌云翔，馬滿好，袁衛衛，等.作戰模型與模擬［M］.湖南：國防科技大學出版社，2006：126－185.

［17］張效成，張陽，徐錟.經濟類數學分析（下冊）［M］.天津：天津大學出版社，2005：68－156.

［18］孫巨為.作戰力量體系優化問題研究［D］.河北：石家莊陸軍指揮學院，2011.Sun Juwei.Research on the optimization problem of combat power system［D］.Hebei：Shijiazhuang Army Command College，2011.

［19］金偉新，肖田元.作戰體系復雜網絡研究［J］.復雜系統與復雜性科學，2009，6（4）：12－25.Jin Weixin，Xiao Tianyuan.Research on the combat SoS complex network［J］.Complex Systems and Complexity Science，2009，6（4）：12－25.

［20］БусленкоН П.Моделированиесложныхсистем［M］.Москва：Издатериство《Наука》，1978：24－121.

［21］Dean J R.Warfare analysis laboratory 2000［J］.Johns Horkings Apl Technical Digest，2000，21（2）：231－237.

［22］Moffat J.Complexity Theory and Network Centric Warfare［M］.Washington：CCRP Press，2000：65－89.

［23］James M T.On integration and adaptation in complex service systems［J］.Journal of Systems Science and Systems Engineering，2008，17（4）：48－54.