基于道路狀況的冷鏈物流配送路徑優化

韓 印，師 攀 （上海理工大學，上海200093）

HAN Yin, SHI Pan (University of Shanghai for Science and Technology, Shanghai 200093, China)

0 引 言

我國每年果品腐蝕損壞近1 200 萬噸，蔬菜1.3 億噸，經濟損失超過上千億元。易腐食品特別是初級農產品的大量損耗，尤其在運輸過程中損耗最高，使整個物流費用占到易腐食品成本的70%。因此，迫切需要降低物流成本。

優化配送路徑是降低物流成本的重要途徑。早在1959 年，Dantzig 和Ramser 在進行一個配送汽油至加油站的問題時就提出了車輛路徑問題[1]。Clarke 和Wright 在此基礎上提出了一種改進的并且較為有效的啟發式算法，Clarke-Wright 節約算法[2]。1987年，Solomon 和Desrosiers 等人將時間窗約束引入到一般的車輛路徑問題中，最早對時間窗的車輛路徑問題進行了研究[3]。但是，對冷鏈物流配送路徑優化的研究還相對較少，Tarantilies 和Kiranoudis 等認為時間的有效性是易腐食品配送的關鍵，提出通過交換路徑中的節點或路徑來進行改進算法優越性的后啟發式算法，但是沒有考慮冷藏[4]。Miroslav Verbic 用線性規劃的方法，從經濟價值角度給出衡量冷鏈中易腐食品質量的主要因素[5]。李宏以傳統時間窗限制下車輛路徑問題為基礎，考慮了生鮮產品腐壞造成的貨損成本以及違反客戶需求時間窗引起的懲罰成本、配送時冷凍設備消耗的成本等，建立了冷鏈物流配送路徑的基本模型，最后進行了算例分析和主要參數的敏感度分析[6]。上述文獻都沒有考慮路況條件，本文在冷鏈物流配送模型的基礎上，考慮路況對配送路徑的影響，構造了一種綜合節約算法，并對10 個客戶進行算例分析，用該算法分別對考慮路況條件的配送模型與沒考慮路況條件的配送模型求解，由結果可知兩個模型得出的最優路徑不同，因此得出結論，研究考慮路況條件的冷鏈物流配送更具有實際意義。

1 冷鏈物流配送模型

1.1 問題描述

冷鏈物流配送路徑優化問題可描述為：一個配送中心擁有多輛汽車，每輛汽車從配送中心出發，為多個客戶送貨，配送結束后配送車輛返回配送中心。

1.2 模型前提假設

（1） 配送中心擁有一定數量的配送車輛，且每輛車載重量一定。

（2） 配送中心不存在缺貨，且客戶的需求量、地理位置、時間窗約束已知。

（3） 配送車輛從配送中心出發，完成配送任務后必須返回配送中心。

（4） 車輛一旦離開前一個客戶點，下一個客戶點便已確定，無中途指派。

（5） 在配送過程中能保持固定溫度，產品損耗只與配送時間有關。

（6） 每條路線上的需求量都小于車輛的裝載量，且每個客戶所需貨物只能由一輛汽車配送。

（7） 每條配送路徑上的運輸長度不能大于配送車輛一次配送最大距離。

（8） 每個客戶對早到或晚到的不滿意程度都符合相同的線性函數關系。

（9） 每條道路等級已知。

1.3 冷鏈物流配送模型建立

模型以綜合成本最低作為目標函數。綜合成本包括：配送車輛的運輸成本、貨損成本、能耗成本以及違反時間窗的懲罰成本。

（1） 配送車輛運輸成本

車輛的運輸成本可表示為：

其中：c為單位里程運輸成本，dij為客戶i到客戶j之間的距離，xijk為0，1 變量，當第k輛車經過（pi,pj）路段時，則xijk為1，否則為0。

（2） 配送過程中的貨損成本

貨損成本包含運輸過程中的貨損成本和服務客戶時車門開啟造成的貨損成本。貨損成本可表示為：

其中：p為生鮮產品的單位成本，xjk為0，1 變量，當第K輛車為j客戶服務時，xjk=1，否則為0。dij為從客戶i到客戶j的距離。zij為路況條件轉換系數，θ1為運輸過程中的貨損系數，θ2為服務客戶時的貨損系數，qj為到達客戶j時車上所剩的貨物量。

（3） 配送車輛制冷的能耗成本

制冷劑消耗量計算簡化公式為：

其中：H為制冷劑消耗量，β 為常數，R為車廂的熱傳系數（W/（m2·K），Sb為車體表面積（m）2，ΔT為車廂內外溫度差（℃）。設ph為制冷劑價格，則車輛行駛過程中消耗制冷劑成本為：

打開車門時消耗的制冷成本為：

其中：fj為車輛在客戶j的服務時間，S為車門面積。

（4） 違反客戶時間窗的懲罰成本

假設客戶j要求的時間窗為[ej,lj]，可接受的時間窗為[Ej,Lj]，tj為配送車輛到達客戶點j的時間。如果送達時間在[Ej,lj]，懲罰成本為0；如果送達時間超過[Ej,Lj]，則懲罰成本為+∞；若在Ej之前則需要等待至Ej，期間貨損系數為θ1；如在[lj,Lj]之間送達，懲罰系數為μ。因此，懲罰成本可表示為：

1.4 冷鏈物流車輛配送路徑優化模型

上述式中式（1） 為目標函數；式（2） 約束配送路徑數不能超過配送車輛總數；式（3） 約束配送車輛的出發點和返回點都為配送中心；式（4）、（5） 約束每個客戶只被一輛車服務一次；式（6） 約束每條路徑上客戶需求總量不得超過配送車輛的載重量；式（7） 要求車輛到達時間必須在客戶要求的時間范圍內；式（8）、（9） 保證時間表的靈活性。

2 基于路況條件下的綜合節約算法

綜合節約算法與原有節約里程法的不同之處是不單純的以距離作為節約的判斷依據，而是綜合考慮了道路狀況，將距離節約轉化為綜合節約。

綜合節約的基本思想是綜合考慮配送道路通行狀況，并通過當地交管部門獲取道路狀況系數zij，通過道路平均運行速度進行換算，然后對運輸成本、貨損成本、制冷成本分別節約，最后對其進行綜合，如表1。其方法如下：

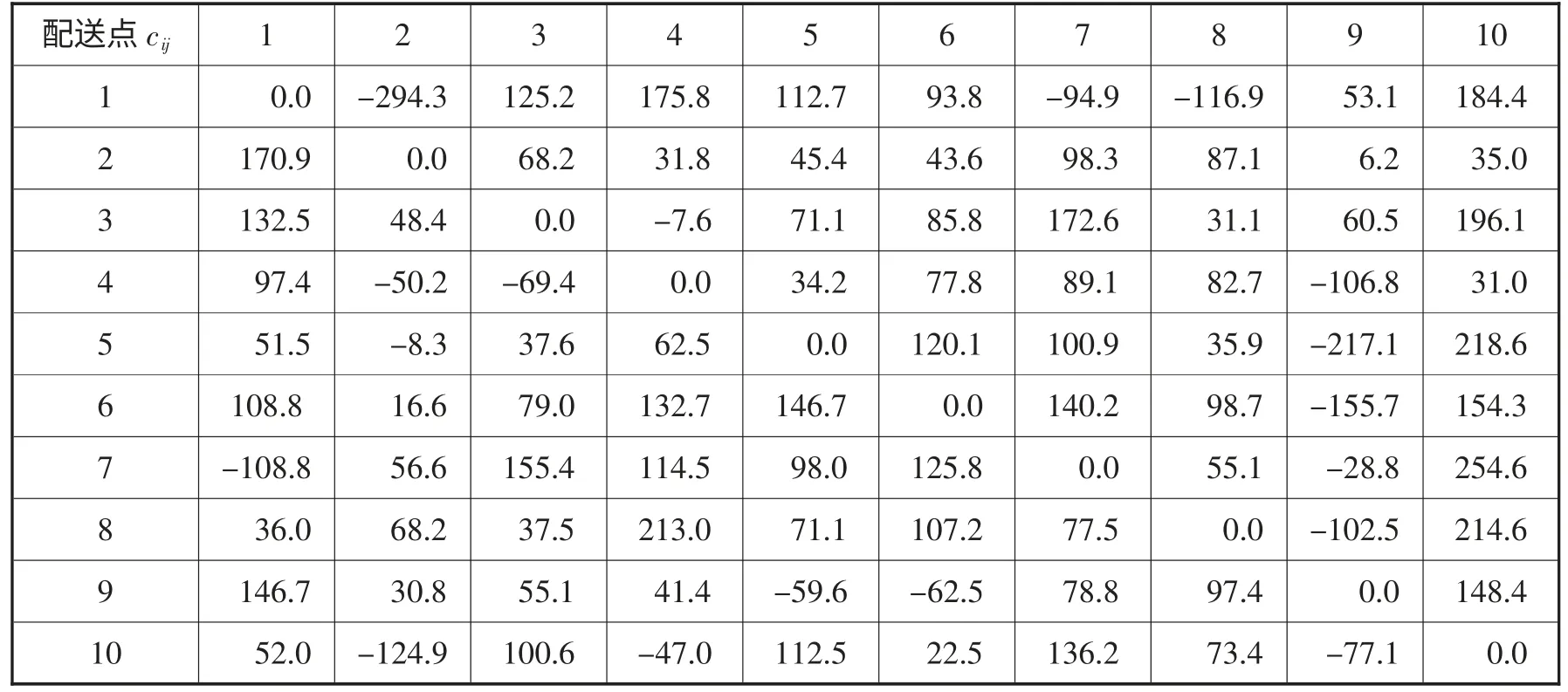
表1 綜合節約成本

（1） 每一個節點pi與配送中心p0連接，產生n條僅含一個點的路徑p0-p1-p0，根據節約算法，連接任意兩點i、j后算出節約運輸成本Δc1=c0i+c0j-cij。然后依次算出節約貨損成本節約制冷成本

（2） 將三個節約成本進行綜合得到總節約成本Δc=Δc1+Δc2+Δc3。

（3） 以時間窗為標準，將所有客戶依次排序。

（4） 以配送中心為起點，將時間窗最靠前的客戶作為第一條路線上的第一個客戶，并在Δc表格中找出總節約成本最大的客戶。依此類推，直到達到時間窗或者車容量限制，這作為第一條路線。

（5） 刪掉第一條線路上的客戶，重復步驟4，直到所有客戶都在線路上。

3 算例分析

本文給出10 個客戶數算例驗證上述算法，具體描述如下：某配送中心向10 個客戶配送某種蔬菜，客戶i的需求量為Qi，配送中心到各配送點的需求量和配送距離由表2 給出，在i的服務時間為fi以及客戶要求到達的時間范圍[ej,lj]由表3 給出，采用小型貨車的載重量為4t，且配送過程中平均行使速度為30km/h，最后返回配送中心。

單位運輸成本c=2 元/km，蔬菜單價為4 000 元/t，運輸過程中的貨損系數θ1為3%，裝卸過程中的貨損系數θ2為0.2%，車內溫度為-20℃，車外溫度為30℃，車輛使用液態氮為制冷劑，每千克制冷劑價格為4.5 元，β=0.19,ph=4.5，R=0.4,sb=16, Δt=50。

結果分析：

根據產品配送的具體要求，運用改進后的節約算法對問題進行求解，得到的優化結果為：

表2 配送距離及各配送點的需求量

表3 各配送點的時間窗及服務時間

下面根據沒有考慮路況條件的車輛配送模型，利用上述算法求出最優路徑，并把所得路徑給出以供比較。

比較上述路徑可知：兩個模型所得路徑完全不同，考慮道路狀況的模型將實際配送的道路狀況考慮在內，更加具有實際意義。

4 結 論

本文在一般冷藏配送模型的基礎上，充分考慮了實際道路狀況，通過將道路狀況進行簡單的轉化，構建了考慮道路狀況的冷藏物流配送路徑優化模型。模型以包括制冷成本、運輸成本、貨損成本、違反時間窗的懲罰成本在內的總成本最小為目標函數，以車載重量、時間窗為約束。在算法上，構建了基于道路狀況的綜合節約算法，并用該算法找出一個10 個客戶算例最優路徑。最后通過比較一般冷藏物流配送模型跟考慮實際道路狀況的路徑優化模型所得到的最優路徑進行比較，可知兩個模型求出的最優路徑是不相同的，從而得出建立考慮道路狀況的冷藏物流配送模型更加具有實際意義。

[1] Dant Zig G, Ramser J. Theruek dispatehing problem[J]. Management Seienee, 1959(6):80-91.

[2] Clark G, Wright J. Seheduling of vehieles from aeentral depotto anumber of delivery Points[J]. OPens, Researeh, 1964(4):15-18.

[3] Solomon, M. M.. Algorithm for the Vehiele Routing and Seheduling Problems with Time—Windows Constraints[J]. OPerationsreseareh, 1987(2):254-265.

[4] Tarantilis C D, Kirannoudis C T. Ameta-heuristic algorithm for the efficient distribution of perishable foods[J]. Joumal of Food Engingeering, 2001,50:1-9.

[5] Miroslav Verbic. Discussing the parameter of preservation of perishable goods in a cold logistic chain model[J]. Applied Economics, 2006,38:137-147.

[6] 李宏. 城市冷鏈物流配送車輛問題的研究[D]. 長沙：長沙理工大學（碩士學位論文），2006.