基于四元數(shù)表示法的機器人基坐標系標定方法

王偉，劉立冬，王剛，贠超

(北京航空航天大學 機械工程及自動化學院，北京100191)

工業(yè)機器人具有較大的靈活工作空間和較高的重復(fù)定位精度，已經(jīng)被廣泛應(yīng)用在自動化生產(chǎn)中.為了滿足更加精細的作業(yè)需求，如何進一步提高工業(yè)機器人的定位精度是當前的研究熱點之一.標定工業(yè)機器人的基坐標系是提高機器人定位精度的有效手段之一.機器人基坐標系一般設(shè)置在機器人底座的固定位置，當?shù)?關(guān)節(jié)轉(zhuǎn)角為0時，基坐標系與第1連桿坐標系重合.通常需要利用標定方法才能獲得機器人基坐標系在世界坐標系中的精確位姿.精確標定機器人基坐標系，在機器人離線編程［1］、多機器人協(xié)調(diào)［2］和機器人控制［3］等領(lǐng)域具有重要的意義.

Haytti模型［4］、CPC 模型［5］、S 模型［6］和指數(shù)積模型［7］等被廣泛應(yīng)用于機器人運動學參數(shù)的標定，而有關(guān)機器人基坐標系標定的研究則較少.

目前國內(nèi)外有關(guān)機器人基坐標系標定的研究成果可分為:快速標定和精細標定.快速標定適用于工業(yè)現(xiàn)場的機器人基坐標的簡便標定.快速標定技術(shù)方法可分為3類.

第1類是采用球面、圓柱面和平面等特殊幾何形狀［8-9］.利用機器人末端與特殊幾何形狀接觸，從而將開鏈機器人轉(zhuǎn)化為閉鏈結(jié)構(gòu)，根據(jù)不同接觸位形建立非線性不相容方程組，求解該方程組的最小二乘解，實現(xiàn)機器人基坐標系的標定.

第2類采用線性位移傳感器等增量式測量設(shè)備.文獻［10］集成了線性位移傳感器，提出了一種“相對標定”的想法.這種標定方法包括的標定步驟多，包括的誤差因素較多.

第3類采用單目或雙目視覺標定技術(shù)［11-12］，其數(shù)學模型與第1類標定方法相同.視覺標定不需要實際的物理接觸，測量范圍更大，有利于提高最終的標定精度，但是攝像頭本身的精確度會影響標定結(jié)果.

精細標定往往需要采用外部的精確測量設(shè)備，并設(shè)計相應(yīng)的離線標定算法.典型的測量設(shè)備為激光跟蹤儀［13］、三維坐標測量機和被動式機器人測量臂［14］等.精細標定方法的周期較長，一般適用于離線場合.文獻［15］利用瞬時軸法標定了雙臂協(xié)調(diào)機器人的基坐標系，提高了旋轉(zhuǎn)矩陣的正交性.文獻［16］對不精確的旋轉(zhuǎn)矩陣做奇異值分解，獲得了接近于單位齊次矩陣的真實旋轉(zhuǎn)矩陣.

本文采用四元數(shù)表示法來提高機器人基坐標系的旋轉(zhuǎn)矩陣的正交性.本文建立了機器人運動學模型，設(shè)計了基坐標系的初始標定方法，提出了四元數(shù)表示法的基坐標系的精確標定方法，完成了標定試驗，對比了標定前后機器人的精度.

1 運動學建模

選定{S}為機器人基坐標系，工具坐標系{T}與末端被測點坐標系重合.當機器人的全部關(guān)節(jié)轉(zhuǎn)角都處于理論零位，即q={0}時，{S}和{T}之間的剛體位移定義為參考位形gst(0).

對于每一個關(guān)節(jié)，構(gòu)造一個螺旋ξi.對于轉(zhuǎn)動關(guān)節(jié)，關(guān)節(jié)螺旋 ξi=［viωi］T，vi= － ωi× Oi，ωi∈R3是關(guān)節(jié)軸線方向上的單位矢量，Oi∈R3為軸線上的任一點.對于移動關(guān)節(jié)，關(guān)節(jié)螺旋ξi=［vi0］T，vi∈R3是指向移動方向的單位矢量.

利用指數(shù)積公式將各關(guān)節(jié)的運動加以組合，可得n個關(guān)節(jié)的串聯(lián)機器人正向運動學方程:

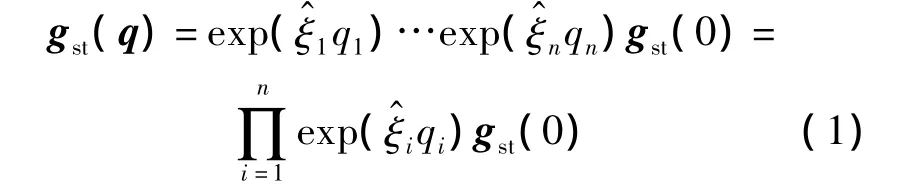
往往測量坐標系{M}與機器人基坐標系{S}不重合，后者相對于前者存在一個剛體位移gms.在測量坐標系{M}下描述的機器人正運動學方程為

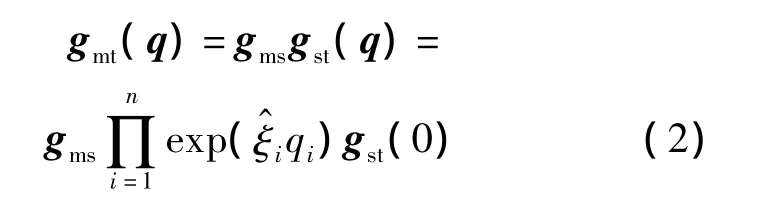
2 基坐標系初始標定

設(shè)末端相對于測量坐標系的位姿gmt(q)=，基坐標系相對于測量坐標系的位姿，末端相對于基坐標系的位姿利用矩陣的分塊乘法，由式(2)，有

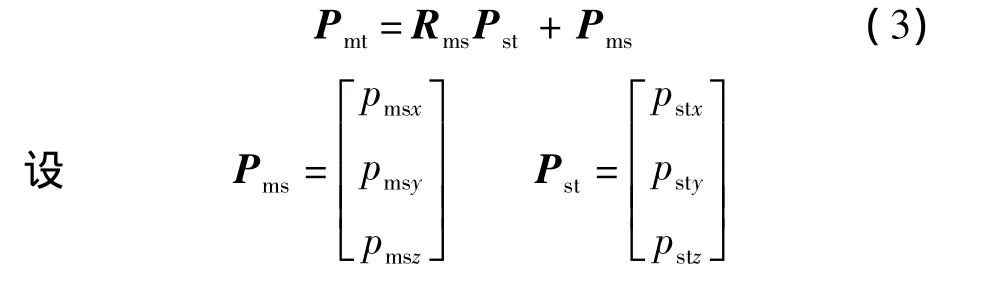
選取5個不共面的TCP，依次記為

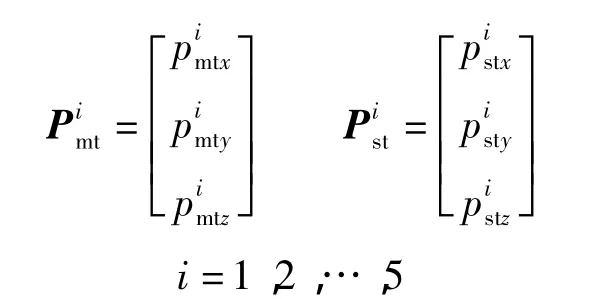
由式(3)，依次做4次減法可得

Rms包括9個未知數(shù)，式(4)可以分解為12個獨立方程，那么式(4)為不相容方程組.對式(4)兩端做轉(zhuǎn)置，可得

令RTms=［x1x2x3］，則由式(5)可得

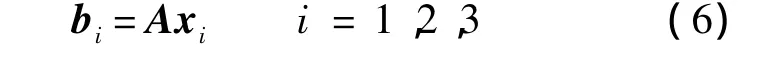
式中，bi和A為已知量;xi為待求量.

建立不相容方程組，可得

由于A為列滿秩，可得

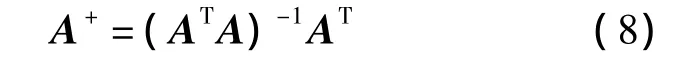
由式(7)，可以求得Rms的3個列向量，以確定基坐標系相對于測量坐標系的姿態(tài).由式(3)可得

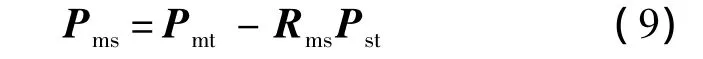
利用式(9)即可求得Pmt，從而確定基坐標系相對于測量坐標系的位置.由式(7)和式(9)可以完成基坐標系的初步標定.

3 基坐標系精細標定

利用上述初步標定方法，可以獲得基坐標系的初步位姿g'ms(q).但是由于測量誤差和計算截斷誤差的存在，導(dǎo)致g'ms(q)中的旋轉(zhuǎn)矩陣不能滿足單位矩陣的正交性.在基坐標系精細標定中，利用四元數(shù)表示法來解決旋轉(zhuǎn)矩陣的正交性.

3.1 單位四元數(shù)表示法

描述兩坐標系之間的姿態(tài)可以用3個獨立元素來描述.單位四元數(shù)是一種描述兩個正交坐標系之間的相對姿態(tài)的數(shù)學表示法.單位四元數(shù)僅需要4個元素，需滿足一個約束條件.而旋轉(zhuǎn)矩陣包括9個元素，則需滿足6個約束條件.相對而言，四元數(shù)表示法比旋轉(zhuǎn)矩陣更加簡潔，且二者之間存在等效變換關(guān)系.

若存在四元數(shù)q，設(shè)為q=q0+iq1+jq2+kq3，令=iq1+jq2+kq3，那么

設(shè)與之對應(yīng)的旋轉(zhuǎn)矩陣為R，那么由關(guān)節(jié)螺旋定義可得

利用 Rodrigue 公式［17］，可得

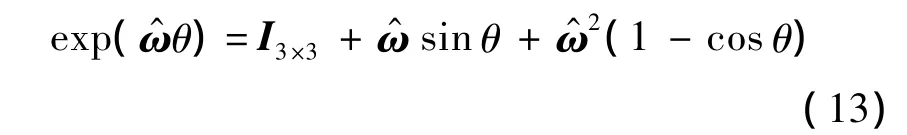
式中

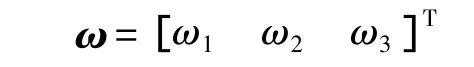
將式(10)、式(11)和式(13)代入式(12)，可得

式中

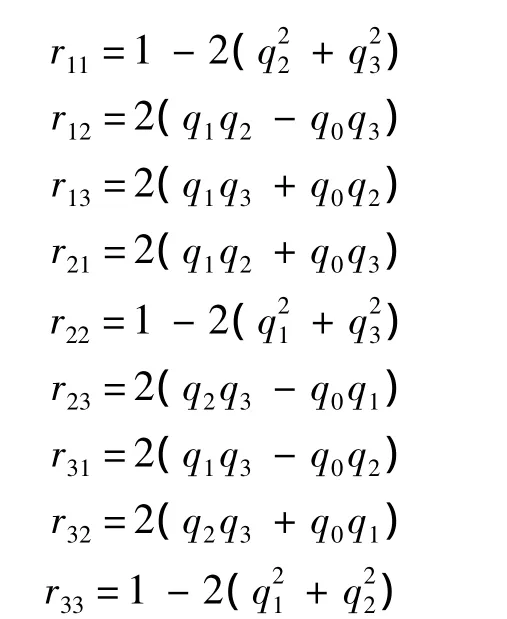
3.2 旋轉(zhuǎn)矩陣的優(yōu)化

利用式(7)標定所得的初步旋轉(zhuǎn)矩陣不能滿足旋轉(zhuǎn)矩陣的正交性，因此需要優(yōu)化初步標定結(jié)果.旋轉(zhuǎn)矩陣優(yōu)化就是定義一個目標函數(shù)，當四元數(shù)變量取得最優(yōu)值時，目標函數(shù)取極小值.

設(shè)與 q等效的旋轉(zhuǎn)矩陣為 R，令 R=Rot(q0，q1，q2，q3).定義 R 與 Rmt之間的距離函數(shù)為

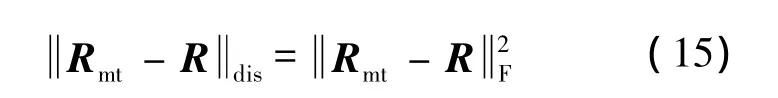
其中F表示為矩陣的F范數(shù).選定上述距離函數(shù)為優(yōu)化目標函數(shù)C，則

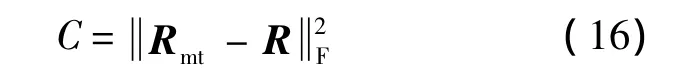
當R為正交化結(jié)果時，應(yīng)滿足以下方程:

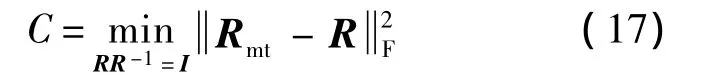
那么

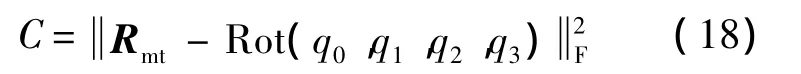
且滿足:

方程(18)可視為一個數(shù)學優(yōu)化問題，即求得多變量函數(shù)C的最小值，并且滿足約束條件q20+q21+q22+q23=1.拉格朗日乘子法為該類優(yōu)化問題提供了有效的求解方法.定義拉格朗日方程如下:

則式(20)可化為

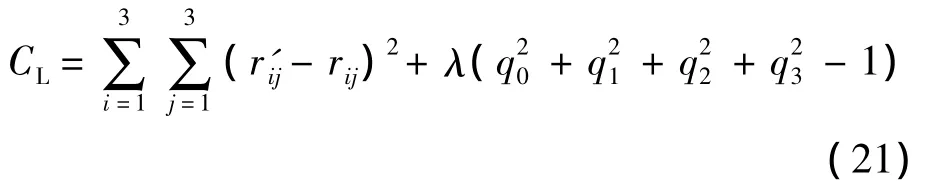
將式(14)代入式(21)，可得

當式(22)取得極值時，滿足以下非線性方程組:

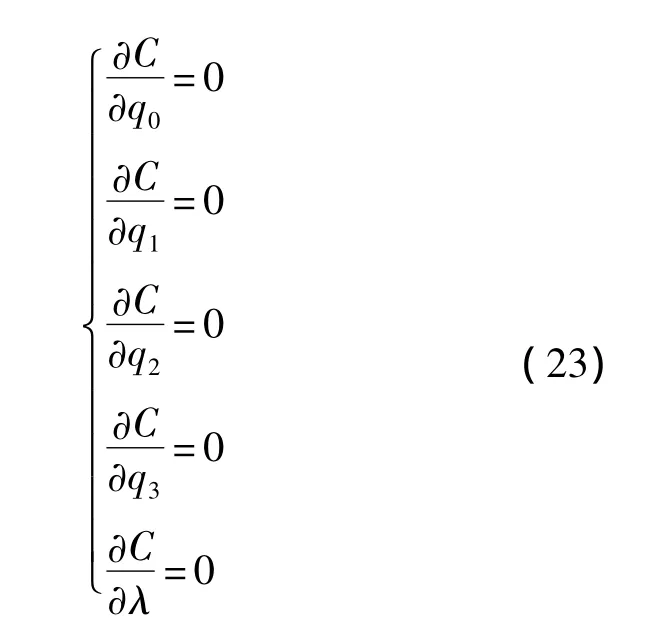
列出上述方程組的顯示表達式為

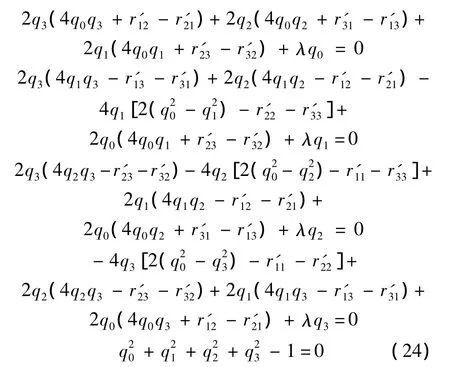
式(24)為非線性方程組，包括5個變量和5個方程.利用牛頓迭代法即可求出式(24)的數(shù)值解

當q*=［qO0qO1qO2qO3］取得該數(shù)值解時，其對應(yīng)的旋轉(zhuǎn)矩陣與初步標定的旋轉(zhuǎn)矩陣距離最近，從而實現(xiàn)旋轉(zhuǎn)矩陣的精細標定.

4 標定試驗

本節(jié)介紹機器人基坐標系標定的試驗系統(tǒng)組成、標定步驟、標定數(shù)據(jù)和標定前后機器人精度對比.

4.1 標定試驗系統(tǒng)

在運動學參數(shù)標定試驗中，試驗系統(tǒng)由FARO ARM、末端球形靶標和ABB公司的標準工業(yè)機器人IRB 1410組成，如圖1所示.圖1中{T}表示待測量的靶標坐標中心，視為工具坐標系.{S}為IRB 1410機器人的基坐標系，{M}為FARO ARM的測量坐標系.IRB1410機器人的自由度數(shù)為6，其幾何參數(shù)的名義值為:l1=170 mm;l2=475 mm;l3=600 mm;l4=1195 mm;l5=720 mm.在{S}下，靶標相對于機器人手腕中心的位置偏移量為(－14.17 mm，－12.10 mm，251.39 mm).

4.2 試驗步驟和數(shù)據(jù)

在圖1所述標定系統(tǒng)中，F(xiàn)ARO ARM可以直接測量出靶標中心{T}在{M}下的位置坐標.讀取IRB 1410的關(guān)節(jié)轉(zhuǎn)角，利用式(1)，可以獲得靶標中心{T}在{S}下的名義位置.而在一次測量中，{S}與{M}之間存在一個固定的剛體變換gms.假設(shè)機器人運動學參數(shù)無誤差，利用四元數(shù)表示法即可精確標定出gms的實際值.從而將測量所得位置坐標和名義位置坐標轉(zhuǎn)換到同一個坐標系{M}中.

圖1 機器人基坐標系標定系統(tǒng)原理圖Fig.1 Schematic of robot base frame calibration system

考慮到FARO ARM測量臂的測量范圍較小，本次測量一共設(shè)計20個測量點.每個測量點對應(yīng)一個不同的機器人關(guān)節(jié)位形.實際測量過程如圖2所示.一共測量20個不同的末端位置，3個坐標分量記為{PxPyPz}T，如表1所示，p為末端位置序號.對應(yīng)的機器人關(guān)節(jié)位形q，如表2所示.

圖2 末端坐標測量Fig.2 Coordinate measurement of end

表1 末端位置坐標Table1 Position coordinates of end mm

表2 機器人關(guān)節(jié)位形Table2 Robot’s joint configurations

4.3 標定結(jié)果

本節(jié)分別利用非線性最小二乘擬合、初步標定和精細標定等3種方法對試驗系統(tǒng)中的IRB 1410機器人的基坐標系進行標定，并驗證標定后的機器人末端的精度水平.

1)非線性最小二乘擬合.

將式(3)按行轉(zhuǎn)化為3個非線性方程.每個方程包括4個未知數(shù).分別取5個測量位形，采用最小二乘非線性擬合方法，即可求出4個未知數(shù).所選取的5個測量位形的序號分別是:4，8，11，14，17，標定所得的基坐標系位姿矩陣為

2)初步標定.

利用式(7)和式(9)，即可求出初始標定的基坐標系位姿.所選取的5個測量位形的序號分別是:4，8，11，14，17，標定所得的基坐標系位姿矩陣為

3)精細標定.

利用式(24)，即可求出精細標定的基坐標系位姿.所選取的5個測量位形的序號分別是:4，8，11，14，17，標定所得的基坐標系位姿矩陣的四元數(shù)為

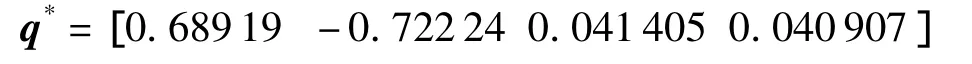
對應(yīng)的齊次矩陣為

4)標定結(jié)果對比.

分別利用最小二乘法擬合標定結(jié)果、初始標定結(jié)果和精細標定結(jié)果，對4.2節(jié)中的20組機器人位形和對應(yīng)的末端位置進行精度驗證.驗證結(jié)果如圖3所示，其中縱坐標為所測點的名義坐標與測量坐標之間的絕對定位誤差，橫坐標是所測點的序號.

圖3 精度驗證和比較Fig.3 Verification and comparation of accuracy

如果采用最小二乘擬合法對機器人基坐標系進行標定，那么第1點處誤差最大，定位偏差為2.35 mm，在第17點處誤差最小，定位偏差為0.045 mm.

如果采用初始標定的機器人基坐標系位姿，那么第1點處誤差最大，定位偏差為3.09 mm，在第17點處誤差最小，定位偏差為0.099 mm.

如果采用本文的精細標定方法，那么在第5點處誤差最大，定位偏差為1.30 mm，在第13點處誤差最小，其定位偏差為0.165 mm.

可見，經(jīng)過基坐標系的精細標定后，所測20個位置的定位誤差帶縮小，各點的定位誤差更加均勻，提高了機器人的定位精度.

5 結(jié)論

本文提出和實施了一種采用四元數(shù)表示法的機器人基坐標系的精確標定方法，提高了基坐標系姿態(tài)矩陣的正交性.

1)初始標定步驟中，建立待標定齊次矩陣的不相容非線性方程組，以最小二乘解作為初始標定結(jié)果.

2)在精細標定中，采用了四元數(shù)法來描述機器人基坐標系的實際位姿，以初始標定位姿與實際位姿偏差矩陣的F范數(shù)為優(yōu)化目標方程，采用拉格朗日乘子法和牛頓迭代法獲得機器人基坐標系的精確標定結(jié)果.

3)搭建了工業(yè)機器人和測量臂組成的標定試驗系統(tǒng)，完成20個測量點的驗證試驗，證明經(jīng)過本方法標定后，最大機器人定位誤差減小為1.30 mm.

References)

［1］ Jin X S，Yang X C.Off-line programming of a robot for laser remanufacturing［J］.Tsinghua Science ＆ Technology，2009，14(S1):186-191.

［2］ Pradeep V，Konolige K，Berger E.Calibrating a multi-arm multisensor robot:a bundle adjustment approach［J］.Experimental Robotics Springer Tracts in Advanced Robotics，2014，79:211-225.

［3］ Graig J J.Introduction to robotics:mechanics and control［M］.3rd ed.Upper Saddle River:Pearson Education Inc，2005:10-20.

［4］ Hayati S A.Robot arm geometric link parameter estimation［C］//Proceedings of 22nd IEEE Conference on Decision and Control.San Antonio，Texas:IEEE，1983，22:1477-1483.

［5］ Zhuang H，Roth Z S，Hamano F.A complete and parametrically continuous kinematic model for robot manipulators［J］.IEEE Transactions on Robotics and Automation，1992，8(4):451-463.

［6］ Stone H W，Sanferson A C.A prototype arm signature identification system［J］.Proceeding of IEEE Conference on Robotics and Automation，1987，4:175-182.

［7］ He R，Zhao Y J，Yang S N，et al.Kinematic-parameter identification for serial-robot calibration based on POE formula［J］.IEEE Transactions on Robotics，2010，26(3):411-423.

［8］ Gan Z，Rossano G，Li X，et al.Method for calibrating and programming of a robot application:US，Patent 6，822，412［P］.2004-11-23.

［9］ Gu X，F(xiàn)eng C.A calibration procedure for a system of two coordinated manipulators［J］.International Journal of Robotics and Automation，1995，10(4):152-158.

［10］ Sun Y，Giblin D J，Kazerounian K.Accurate robotic belt grinding of workpieces with complex geometries using relative calibration techniques［J］.Robotics and Computer-Integrated Manufacturing，2009，25(1):204-210.

［11］ Jianbo S U.Base calibration for dual robot system［J］.Control Theory and Applications，1998，15(4):575-582.

［12］ Wang H，Shen S，Lu X.A screw axis identification method for serial robot calibration based on the POE model［J］.Industrial Robot:An International Journal，2009，39(2):146-153.

［13］ Nubiola A，Bonev I A.Absolute calibration of an ABB IRB 1600 robot using a laser tracker［J］.Robotics and Computer-Integrated Manufacturing，2013，29(1):236-245.

［14］ Santolaria J，Aguilar J J，Yanue J A，et al.Kinematic parameter estimation technique for calibration and repeatability improvement of articulated arm coordinate measuring machines［J］.Precision Engineering，2008，32(4):251-268.

［15］ Gan Y，Dai X.Base frame calibration for coordinated industrial robots［J］.Robotics and Autonomous systems，2011，59(7):563-570.

［16］ Ernst F，Richter L，Mmtthaus L，et al.Non-orthogonal tool/flange and robot/world calibration［J］.The International Journal of Medical Robotics and Computer Assisted Surgery，2012，8(4):407-420.

［17］ Murray R M，Li Z，Sastry S S，et al.A mathematical introduction to robotic manipulation［M］.Boca Raton:CRC Press，1994:28.