薄板的后屈曲損傷分析與疲勞壽命預估

肖浩，胡偉平*，張淼，孟慶春

(1.北京航空航天大學 航空科學與工程學院，北京100191;2.中國空間技術研究院，北京100094)

在航空航天、管道運輸等工程領域，結構的穩定性問題一直受到重點關注.結構的屈曲問題早在18世紀由Euler和Lagrange提出，在這之后，Duncan［1］對不均勻柱進行了研究，為屈曲臨界載荷推導了封閉形式的表達式.此后，對于封閉解的研究較少.1999 年，Elishakoff和 Rollot［2］才發現了新的封閉解.但工程結構的實際屈曲載荷明顯要低于由理論解給出的屈曲臨界載荷，當時的理論無法解釋這一現象.

1941 年，von Kármán 和 Tsien［3］根據非線性大撓度理論，提出了板殼后屈曲分析的一般方法以及非線性屈曲理論.Donnell和 Wan［4］于1950年將非線性大撓度分析推廣到非完善圓柱薄殼.Koiter［5］用攝動法研究了彈性結構的初始后屈曲性態，導出了臨界壓力與缺陷參數之間的關系，并提出了初始缺陷敏感度的概念.1968年，Stein［6］提出了非線性前屈曲一致理論，解釋了經典線性理論與實驗之間差異的原因.非線性屈曲分析考慮了結構屈曲前的變形，計算結果更符合實際情況.

以von Kármán大撓度理論為依據，對于單一的屈曲和后屈曲問題已有大量的研究成果，但在實際工程應用中，當薄壁構件受到循環載荷作用時，可能會出現屈曲問題與疲勞問題的耦合［7-8］，即結構可能在反復進入后屈曲狀態下發生疲勞破壞，或是在產生一定的疲勞損傷累積后發生屈曲或后屈曲破壞.

目前，國內外很多學者主要研究構件在循環載荷下屈曲后屈曲過程中模態的改變［9-10］，以及臨界載荷和極限載荷隨著循環次數的增加而產生的變化［11-12］，很少有研究將屈曲分析與疲勞損傷分析進行耦合，并進一步預估構件的疲勞壽命.

本文基于連續損傷力學理論與方法，研究結構在后屈曲情況下的損傷以及在疲勞載荷作用下屈曲與疲勞損傷的耦合特性.首先采用有限元方法，通過線性屈曲分析得到屈曲臨界載荷和屈曲模態，進而采用大撓度理論，將線性屈曲的一階屈曲模態作為初始擾動，進行薄板的非線性屈曲分析，得到屈曲臨界載荷.其次，根據損傷力學理論與方法建立薄板材料在單次加載過程中的損傷演化方程以及參數識別方法，并根據非線性屈曲分析結果進行后屈曲損傷分析.最后，考慮疲勞載荷的作用，基于損傷力學理論，采用有限元數值方法進行求解，考慮每次加載引起的疲勞損傷與后屈曲應力應變場的耦合作用，通過反復迭代計算，給出結構疲勞壽命.本研究為結構在后屈曲情況下的疲勞特性分析提供了一種新的分析方法和實現途徑，可以應用于飛行器中某些特殊受力狀態下薄壁構件的疲勞壽命分析.

1 薄板的線性屈曲分析

板的線性屈曲分析是一種最常規的分析方法，可以給出結構的各階屈曲臨界載荷以及相應的屈曲模態.

1.1 薄板的有限元模型

考慮一四邊簡支且在某兩對邊受均勻壓力的方形薄板，板邊長a=40mm，板厚h=0.6mm，材料為LC9CgS1［13］，其幾何形狀及載荷如圖1所示.

圖1 結構幾何模型Fig.1 Geometry model of the structure

載荷大小為Px=40 N/mm，四邊簡支板的邊界條件為

式中w為結構變形撓度.

在ANSYS中建立薄板的有限元模型.選擇Shell181單元，該單元適用于薄到中等厚度的殼結構，單元有4個節點，每個節點有6個自由度，適用于結構的幾何非線性分析.

1.2 特征值屈曲分析

建立有限元模型后，在ANSYS軟件中進行特征值屈曲分析.計算得到薄板的一階屈曲臨界載荷為34.6 N/mm.

通過特征值屈曲分析能夠給出結構屈曲模態，能為結構設計提供參考，并為后續的非線性屈曲分析提供初始擾動.

2 板結構的非線性后屈曲分析

在工程實際中，由于線性屈曲分析忽略了屈曲前變形的影響，導致過高地估計了結構的臨界載荷.因此，為了提高分析的精度，更多地采取非線性屈曲分析方法進行結構穩定性分析.

2.1 非線性屈曲分析方法

非線性屈曲分析的目的是求解結構從穩定平衡過渡到不穩定平衡的臨界載荷，結構的載荷臨界點可以分為兩種類型:分叉臨界點和極值臨界點［14］.

分叉臨界點的特征是:結構在基本載荷-位移平衡路徑Ⅰ的附近還存在另一分叉平衡路徑Ⅱ.當載荷達到臨界值Pcr時，如果結構或載荷受到一微小擾動，載荷-位移曲線將沿分叉平衡路徑發展，其載荷-位移曲線如圖2(a)所示.

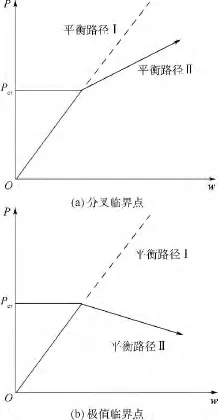
圖2 屈曲載荷臨界點Fig.2 Critical point of buckling load

極值臨界點的特征是:當載荷達到臨界值時，如果載荷位移有微小變化，將分別發生位移的跳躍和載荷的快速下降，其載荷-位移曲線如圖2(b)所示.

利用有限元軟件進行結構的非線性屈曲分析，需要在施加沿板面內壓縮載荷的同時，對結構施加一橫向小擾動，通過失穩點的載荷-位移曲線計算屈曲臨界載荷.

2.2 非線性屈曲分析結果

以特征值屈曲分析得到的第一階屈曲模態作為初始幾何擾動進行非線性屈曲分析，得到失穩點的離面位移隨外載荷的變化曲線，如圖3所示.從該曲線可以判斷出非線性屈曲的臨界載荷為31.5 N/mm.當外載荷達到非線性屈曲臨界載荷時，結構進入后屈曲，屈曲前和屈曲后對應結構的兩個不同的平衡路徑，平衡路徑的轉換也是因為結構上微小擾動的緣故.圖4為結構失穩部位的von Mises應力隨外載荷的變化曲線，可以看出，微小擾動在前屈曲階段對結構的應力影響很小，當外載荷達到屈曲臨界載荷后，結構發生屈曲并進入另一個平衡狀態，此時結構的應力隨外載荷增加而顯著增大.

圖3 失穩點離面位移隨外載的變化曲線Fig.3 Variation curve of deflection of instability point with external load

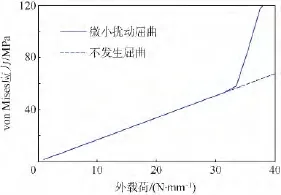
圖4 失穩點的von Mises應力變化曲線Fig.4 Variation curve of von Mises stress of instability point

3 板結構的后屈曲損傷分析

通過板的后屈曲分析可知，當板所受載荷超過屈曲臨界載荷時，板進入后屈曲狀態，此時結構失穩部位的應力迅速增加.當板承受最大載荷超過屈曲臨界載荷的循環載荷時，板在每一次載荷循環中都將經歷一次后屈曲，因此為了預估板的疲勞壽命，首先需要進行板在后屈曲狀態下的損傷分析.下面擬采用連續損傷力學理論與方法，建立結構在后屈曲狀態下的損傷分析模型.

3.1 損傷演化模型

根據連續損傷力學理論，在疲勞載荷作用下，材料的損傷將引起材料有效承載面積的下降.在各向同性損傷的情況下，引入損傷度D描述這一物理過程［15］，令

在單向受力狀態下，建立材料單元的力平衡方程:

對于受損傷的材料單元，其真實應變為

在三維受力情況下，對于各向同性材料，根據應變等價原理，得到含損傷線彈性體本構關系為

式中，λ和μ為拉梅常數;σij和εij分別為應力張量和應變張量分量.

單軸受力情況下，以應變為基本變量，含損傷材料應變能密度為

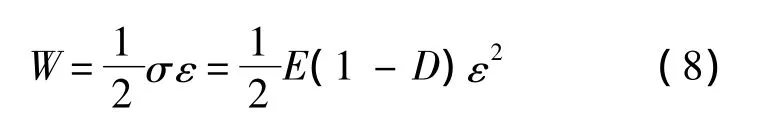
根據熱力學原理，引入損傷驅動力［16］:

單軸受力情況下，有

對處于復雜受力狀態下的結構而言，引入損傷力學等效應變:

式中εm為平均應變.

采用如下形式的損傷演化方程［17］:

式中，Ymax為損傷力學驅動力峰值;Yth為損傷力學驅動門檻值;N為載荷循環次數;mk為材質參數.式(12)可以寫成如下應變形式的表達式:

式中，β和εth為材質參數;εmax為最大損傷力學等效應變.式(13)需要通過材料標準件疲勞試驗結果識別.

3.2 參數識別

3.1節已經建立了材料在疲勞載荷作用下的損傷演化方程，方程中包含有β，mk，εth等材質參數，這些參數需要根據材料標準件的疲勞試驗結果來確定.

對于光滑試樣，根據單軸受力的本構關系可得

式中，D0，1為應力集中系數KT=1試件的初始損傷;σ0，max為交變載荷引起的最大應力;σ1，th為KT=1時材料發生疲勞損傷的應力門檻值.

對損傷演化方程積分，可得

式中，Nf為裂紋萌生壽命;m為材質參數.式(15)可以寫為

式(16)即為KT=1時材料的裂紋萌生壽命和最大應力之間的關系.根據這一應力-壽命表達式，結合材料的疲勞試驗結果，就可以確定式(16)中的材質參數 β，mk，D0，1及 σ1，th.LC9CgS1材料的靜力力學性能如表1所示.當KT=1，應力比R=0.1時，LC9CgS1材料標準件的疲勞壽命如表2所示.

表1 LC9CgS1材料的靜力力學性能參數Table1 Static mechanical properties of LC9CgS1

表2 KT=1，R=0.1時 LC9CgS1 材料的疲勞試驗結果Table2 Fatigue test results of LC9CgS1 when KT=1，R=0.1

根據以上疲勞試驗結果并假設實驗結果中離中值壽命曲線最遠點的實驗點對應的材料初始損傷度為0，可以得到損傷演化方程中的材質參數如表3所示.

表3 KT=1，R=0.1時LC9CgS1的材質參數Table3 Material parameters of LC9CgS1 when KT=1，R=0.1

計算結果與實驗點的對比如圖5所示.

圖5 KT=1，R=0.1時計算結果與實驗點對比曲線Fig.5 Comparison of experimental points and calculation results when KT=1，R=0.1

從圖5可以看出KT=1，R=0.1時擬合的材質參數是合理的.

4 板結構疲勞壽命預估

當板受到的最大載荷超過屈曲臨界載荷的疲勞載荷作用時，每一次載荷循環中，板都要進入后屈曲狀態，造成局部材料的損傷，這一損傷又會降低下一次加載時板的屈曲臨界載荷，這種屈曲與疲勞損傷的耦合特性難以用閉合形式的方程描述.因此，基于損傷力學理論，采用有限元數值解法，通過反復迭代的后屈曲分析和疲勞損傷分析來預估板的疲勞壽命.

4.1 損傷力學-有限元數值解法

利用ANSYS軟件中的APDL語言控制求解過程，將ANSYS軟件計算得到的應力場代入損傷演化方程，計算結構的損傷場，給出各單元損傷度;根據單元損傷度計算各單元的等效彈性模量，在ANSYS軟件中給各單元重新賦值，再次計算下一個載荷作用下的應力場.如此迭代計算，在ANSYS平臺中，基于損傷力學理論，采用有限元數值解法對構件進行疲勞壽命預估.

具體做法如下:

1)利用ANSYS軟件計算結構在某一載荷循環下的應力應變場.

2)根據上一步計算得到的應力應變場，通過APDL語言對ANSYS軟件進行二次開發，計算每個單元的損傷力學等效應力.

3)利用APDL語言，在ANSYS軟件中計算每個單元在ΔN次載荷循環之后，損傷度的增量:

式中，βk為材質參數;εe，e，max為單元的最大損傷力學等效應變;εk，th為損傷力學應變門檻值.

那么，可以得到當前各個單元的損傷度:

4)由上述計算得到的各個單元的損傷度可知每個單元的等效彈性模量的變化量，在ANSYS軟件中重新賦予各個單元彈性模量，在上次計算結果基礎上，進行下一個加載循環的應力應變分析.

5)重復步驟2)～步驟4)的過程，直到某一單元損傷度達到或超過1，此時的ΔN的累積值即為疲勞裂紋萌生壽命.

需要說明的是，載荷循環次數步長ΔN需通過不斷減小ΔN的值來進行收斂性驗證.

損傷力學有限元法計算流程如圖6所示.

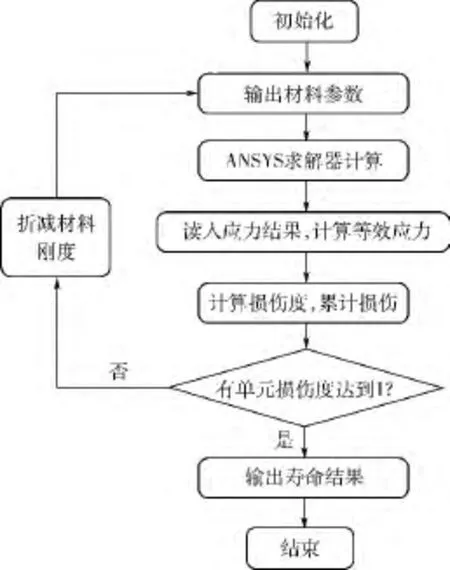
圖6 損傷力學有限元法計算流程圖Fig.6 Calculation flow chart of damage mechanics with finite element method

4.2 計算結果

給定板受到的疲勞載荷為:最大載荷為40 N/mm，載荷比 R=0.1.由于最大載荷大于板的屈曲臨界載荷31.5 N/mm，因此每一次加載循環中板都將進入后屈曲階段.

薄板在后屈曲狀態下，失穩部位局部發生損傷，這一損傷會導致板的總體剛度矩陣發生變化，從而影響下一次加載時的屈曲臨界載荷以及結構位移.圖7顯示了不同損傷階段失穩部位的載荷位移曲線的變化.從圖7可以看出，板的屈曲臨界載荷隨著損傷的增加而減小，失穩點的離面位移隨著損傷的增加而增大.

圖7 不同損傷度下結構失穩點位移變化曲線對比Fig.7 Comparisons of deflection changing curves of instability points in different damage degrees

通過計算，板在上述疲勞載荷作用下的疲勞壽命為6×105次，失效的單元位于失穩點，失穩點周圍的區域是損傷比較大的區域，因為隨著損傷的增大，結構的屈曲臨界載荷會逐漸變小，失穩區域會擴大，這一部分區域損傷也會因此而變大.

4.3 初始幾何缺陷對結構裂紋萌生壽命的影響

在前面考慮后屈曲的疲勞壽命分析中，為了模擬屈曲這一物理過程，在每一次屈曲分析時都對結構施加了擾動.

采用的施加擾動方法是引入初始幾何缺陷，即將第一階線性屈曲位移模態作為初始缺陷施加在板上.然而這里存在一個問題，即作為初始缺陷的一階線性屈曲位移模態的幅值如何選取，不同幅值對板的疲勞壽命的影響程度如何.

因此計算了不同缺陷幅值比(幅值比=幾何缺陷幅值/板厚，無量綱)情況下板的疲勞壽命，如圖8所示.

圖8 裂紋萌生壽命隨幾何缺陷幅值比的變化曲線Fig.8 Changing curve of crack initiation life with different geometric imperfection amplitude ratios

從圖8中可以看出，初始幾何缺陷的大小對板的疲勞壽命影響很大，因此在預估實際結構疲勞壽命時，應首先測量結構的幾何外形，根據測量結果盡量準確估計結構的初始幾何缺陷，以便得到更加準確的疲勞壽命分析結果.

5 結論

基于損傷力學理論構建了薄板后屈曲狀態下的裂紋萌生壽命預估方法，為工程結構考慮后屈曲損傷的疲勞壽命分析提供了一種新的研究方法和手段.

1)首先對板進行了線性屈曲分析，得到了屈曲臨界載荷以及屈曲位移模態，為后續的非線性屈曲分析提供了位移擾動形式.

2)以線性屈曲分析得到的一階屈曲位移模態作為板的初始幾何缺陷，對板進行非線性屈曲分析，得到了板的非線性屈曲載荷，其值要低于特征值屈曲分析得到的屈曲臨界載荷.

3)建立了板后屈曲損傷分析模型，并根據板材料的標準件疲勞試驗結果確定損傷演化方程中的各材質參數.

4)建立了考慮后屈曲過程的板的疲勞壽命分析方法，通過損傷力學-有限元數值解法，可以考慮加載循環過程中板的后屈曲與疲勞損傷的耦合作用.

5)分析初始幾何缺陷的大小對板裂紋萌生壽命的影響，結果表明，初始幾何缺陷對結構的疲勞壽命有很明顯影響，因此，一方面在制造過程中應盡量提高加工精度，減小幾何缺陷;另一方面，在預估結構疲勞壽命時應根據實際測量結果正確估計幾何缺陷的大小，以便給出更符合實際情況的壽命預估結果.

References)

［1］ Duncan W J.Galerkin’s method in mechanics and differential equations，ADA951862［R］.London:Aeronautical Research Council，1937.

［2］ Elishakoff I，Rollot O.New closed-form solutions for buckling of a variable stiffness column by Mathematica［J］.Journal of Sound and Vibration，1999，224(1):172-182.

［3］ von Kármán T，Tsien H.The buckling of thin cylindrical shells under axial compression［J］.Journal of the Aeronautics Science，1941，8(6):303-312.

［4］ Donnell L H，Wan C C.Effect of imperfections on buckling of thin cylinders and columns under axial compression［J］.Journal of Applied Mechanics-transactions of the ASME，1950，17(1):73-83.

［5］ Koiter W T.The stability of elastic equilibrium，AD0704124［R］.Standford:Department of Aeronautics and Astronautics of Standford University，1970.

［6］ Stein M.Some recent advances in the investigation of shell buckling［J］.AIAA Journal，1968，6(12):2339-2345.

［7］ Kong C，Bang J，Sugiyama Y.Structural investigation of composite wind turbine blade considering various load cases and fatigue life［J］.Energy，2005，30(11):2101-2114.

［8］ Rhead A T，Butler R，Hunt G W.Post-buckled propagation model for compressive fatigue of impact damaged laminates［J］，International Journal of Solids and Structures，2008，45(16):4349-4361.

［9］ 李世榮，劉平.彈性地基上Euler-Bernoulli梁的熱屈曲模態躍遷特性［J］.應用力學學報，2011，28(1):90-94.Li S R，Liu P.Thermal buckling mode transition characteristics of Euler-Bernoulli beam on the elastic foundation［J］.Journal of Applied Mechanics，2011，28(1):90-94(in Chinese).

［10］ 賀爾銘，張釗，胡亞琪，等.單軸壓縮載荷下夾層梁結構屈曲及皺曲模擬研究［J］.西北工業大學學報，2012，30(5):668-674.He E M，Zhang Z，Hu Y Q，et al.Buckling and wrinkling study of sandwich beam under uniaxial compression load［J］.Journal of Northwestern Polytechnical University，2012，30(5):668-674(in Chinese).

［11］ 左志亮，蔡健，朱昌宏.帶約束拉桿L形鋼管混凝土短柱的偏壓試驗研究［J］.東南大學學報:自然科學版，2010，40(2):346-351.Zuo Z L，Cai J，Zhu C H.Bias experimental study on the binding L-shaped concrete bars filled with steel tubes［J］.Journal of Southeast University:Natural Sciences，2010，40(2):346-351(in Chinese).

［12］ 夏盛來，何景武，海爾瀚.大展弦比機翼屈曲及后屈曲分析［J］.機械強度，2012，33(6):907-912.Xia S L，He J W，Hai E H.Buckling and post-buckling analysis of the high aspect ration wing［J］.Mechanics Strength，2012，33(6):907-912(in Chinese).

［13］ 吳學仁.飛機結構金屬材料力學性能手冊:靜強度疲勞/耐久性［M］.北京:航空工業出版社，1996:225-353.Wu X R.Manual of metal material mechanics performance of the plane structure:static fatigue strength/durability［M］.Beijing:Aviation Industry Press，1996:225-353(in Chinese).

［14］ 王勖成.有限單元法［M］.北京:清華大學出版社，2003:649-651.Wang X C.The finite element method［M］.Beijing:Tsinghua University Press，2003:649-651(in Chinese).

［15］ Lemaitre J，Desmorat R.Engineering damage mechanics:ductile，creep，fatigue and brittle failures［M］.Berlin:Springer，2005:3-6.

［16］ 張行，崔德渝，孟慶春.斷裂與損傷力學［M］.北京:北京航空航天大學出版社，2006:329-331.Zhang X，Cui D Y，Meng Q C.Fracture and damage mechanics［M］.Beijign:Beijing University of Aeronautics and Astronautics Press，2006:329-331(in Chinese).

［17］ 張淼.構件疲勞壽命預估的多變量損傷力學方法［D］.北京:北京航空航天大學，2009.Zhang M.Multivariate fatigue damage mechanics methods of fatigue life prediction of the structure［D］.Beijing:Beijing University of Aeronautics and Astronautics，2009(in Chinese).