重型軌道車電動(dòng)空壓機(jī)振動(dòng)問題分析及改進(jìn)
張兵奇
重型軌道車電動(dòng)空壓機(jī)
振動(dòng)問題分析及改進(jìn)
張兵奇
某重型軌道車空氣制動(dòng)系統(tǒng)的電動(dòng)空壓機(jī)批量裝車使用時(shí),少量電動(dòng)空壓機(jī)工作時(shí)出現(xiàn)異常振動(dòng)。采用試驗(yàn)方法得到電動(dòng)空壓機(jī)的激勵(lì)頻率,結(jié)合有限元法求得電動(dòng)空壓機(jī)的共振頻率。改變電動(dòng)空壓機(jī)的結(jié)構(gòu),并用有限元法對(duì)改進(jìn)方案進(jìn)行計(jì)算,合理避開了系統(tǒng)共振。通過實(shí)際驗(yàn)證,發(fā)現(xiàn)電動(dòng)空壓機(jī)異常振動(dòng)消失,該問題徹底解決。
電動(dòng)空壓機(jī);異常振動(dòng);共振;有限元計(jì)算
某重型軌道車空氣制動(dòng)系統(tǒng)中用到一款電動(dòng)空壓機(jī),有個(gè)別空壓機(jī)在啟動(dòng)打風(fēng)時(shí)出現(xiàn)明顯的異常振動(dòng),空壓機(jī)及吊架振動(dòng)劇烈。該軌道車空氣制動(dòng)系統(tǒng)的風(fēng)源由3個(gè)空壓機(jī)提供,其中2個(gè)為發(fā)動(dòng)機(jī)自帶空壓機(jī),發(fā)動(dòng)機(jī)工作時(shí)自行運(yùn)轉(zhuǎn),是空氣制動(dòng)系統(tǒng)的主空壓機(jī),在行車時(shí)為軌道車空氣制動(dòng)系統(tǒng)提供風(fēng)源;電動(dòng)空壓機(jī)是輔助空壓機(jī),在軌道車發(fā)動(dòng)機(jī)停機(jī)或發(fā)動(dòng)機(jī)空壓機(jī)故障時(shí)為空氣制動(dòng)系統(tǒng)提供風(fēng)源,作為備用空壓機(jī)使用。空氣制動(dòng)系統(tǒng)關(guān)系到行車安全,風(fēng)源是制動(dòng)系統(tǒng)的原動(dòng)力,空壓機(jī)的正常工作對(duì)行車安全有著十分重要的意義。
1 電動(dòng)空壓機(jī)的結(jié)構(gòu)
該電動(dòng)空壓機(jī)是由電動(dòng)機(jī)、空壓機(jī)、三角皮帶、空壓機(jī)吊架及緊固螺栓等組成。電動(dòng)機(jī)通過皮帶驅(qū)動(dòng)空壓機(jī),電動(dòng)機(jī)及空壓機(jī)用螺栓固定在空壓機(jī)吊架上,空壓機(jī)吊架通過螺栓與車架連接。電動(dòng)機(jī)是三相異步電機(jī),同步轉(zhuǎn)速1 480 r/min。空壓機(jī)為雙缸活塞式空氣壓縮機(jī),車架上的連接件為槽鋼及鋼板,電動(dòng)空壓機(jī)結(jié)構(gòu)如圖1所示。
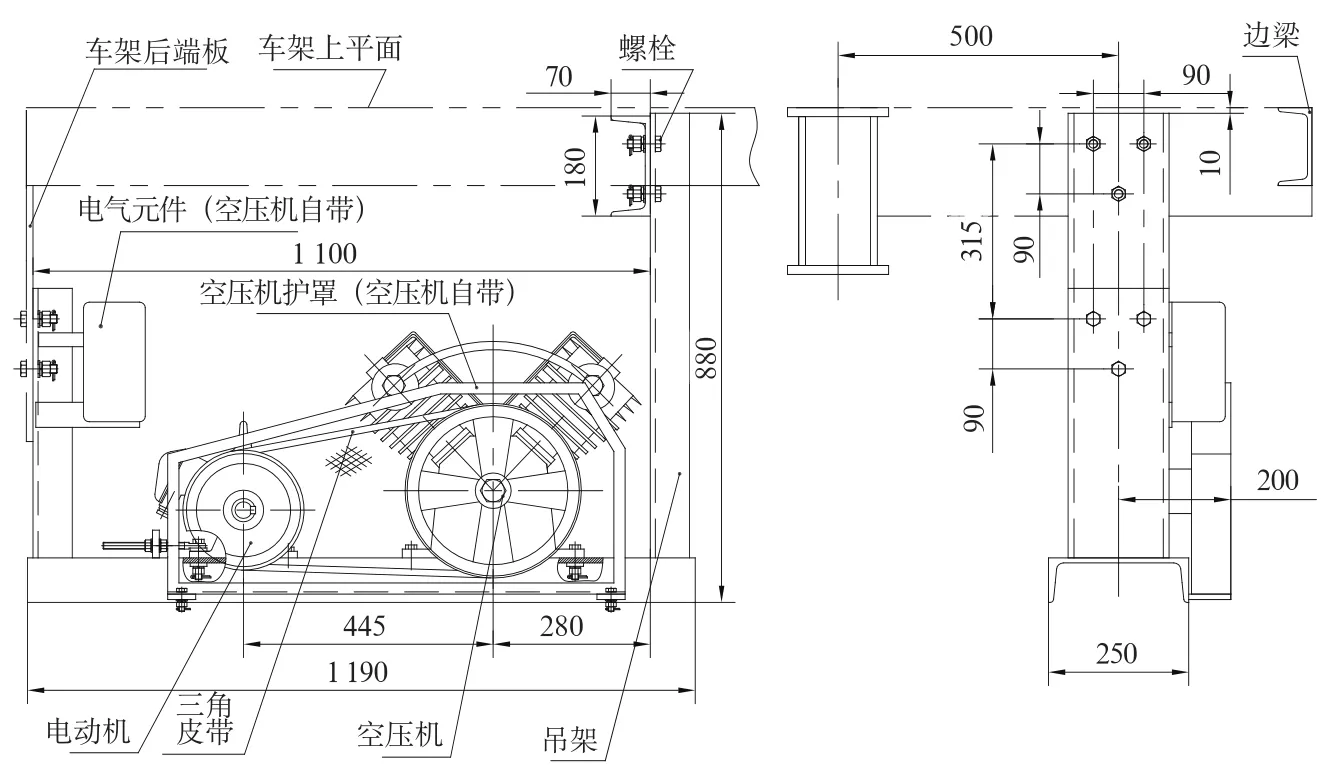
圖1 電動(dòng)空壓機(jī)簡(jiǎn)易裝置圖 (單位:mm)
2 電動(dòng)空壓機(jī)異常振動(dòng)分析
2.1 電動(dòng)空壓機(jī)異常振動(dòng)的描述及原因分析
電動(dòng)空壓機(jī)正常工作時(shí),空壓機(jī)及吊架振動(dòng)明顯,且噪聲偏高;電動(dòng)空壓機(jī)無負(fù)載運(yùn)行時(shí),空壓機(jī)及吊架振動(dòng)幅度稍有減輕,且噪聲有所降低;電動(dòng)空壓機(jī)的電動(dòng)機(jī)單獨(dú)運(yùn)轉(zhuǎn)時(shí)空壓機(jī)及吊架無明顯振動(dòng),但是在電動(dòng)機(jī)停止轉(zhuǎn)動(dòng)過程中的高轉(zhuǎn)速區(qū)段,空壓機(jī)及吊架有明顯振動(dòng)。
根據(jù)以往經(jīng)驗(yàn),電動(dòng)空壓機(jī)異常振動(dòng)通常有以下幾個(gè)原因:①電動(dòng)空壓機(jī)系統(tǒng)的裝配質(zhì)量差,如傳動(dòng)皮帶太松或太緊,空壓機(jī)皮帶盤與電動(dòng)機(jī)皮帶盤出現(xiàn)錯(cuò)位,導(dǎo)致傳動(dòng)過程中皮帶產(chǎn)生過大的附加力;②空壓機(jī)、電動(dòng)機(jī)、空壓機(jī)吊架等連接螺栓預(yù)緊力不足,連接件之間的小間隙產(chǎn)生異常振動(dòng);③空壓機(jī)或電動(dòng)機(jī)的旋轉(zhuǎn)部件的動(dòng)平衡不好,空壓機(jī)工作時(shí)旋轉(zhuǎn)部件的離心力過大,導(dǎo)致異常振動(dòng);④空壓機(jī)吊架剛性不足引起的系統(tǒng)共振。通過對(duì)電動(dòng)空壓機(jī)的檢查,排除了前2項(xiàng)原因,并得出如下判斷:振動(dòng)主要方向沿空壓機(jī)吊架長(zhǎng)度方向,振幅值3~5 mm,屬于異常振動(dòng)。
因主要振動(dòng)是沿空壓機(jī)吊架長(zhǎng)度方向的單自由度振動(dòng),為了便于分析,使用單自由度系統(tǒng)受簡(jiǎn)諧激勵(lì)的動(dòng)力學(xué)模型。將電動(dòng)機(jī)、空壓機(jī)、空壓機(jī)吊架看作1個(gè)振動(dòng)系統(tǒng),其總質(zhì)量為m;空壓機(jī)、電動(dòng)機(jī)的等效激勵(lì)頻率為ω,激勵(lì)振幅為F0,即等效激勵(lì)力為F0sinωt;空壓機(jī)吊架的等效剛度為k;空氣及其他阻力作為阻尼c;根據(jù)參考文獻(xiàn)[2],則系統(tǒng)的運(yùn)動(dòng)微分方程為:

方程(2)的幅頻圖如圖2所示。
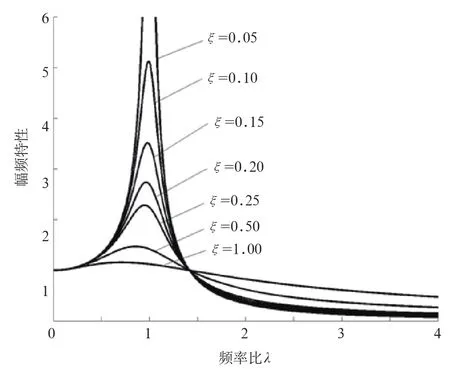
圖2 幅頻圖
因改變阻尼比ξ比較困難,減小空壓機(jī)振動(dòng)的常用方法是改變系統(tǒng)的頻率比和減小激勵(lì)振幅F0,即增加吊架鋼度,使,盡量減小空壓機(jī)的振動(dòng)不平衡,使空壓機(jī)吊架的振動(dòng)幅度小于3 mm。
2.2 電動(dòng)空壓機(jī)共振頻率測(cè)試
系統(tǒng)的共振頻率和激勵(lì)頻率接近時(shí)才會(huì)出現(xiàn)共振,因此,可以根據(jù)激勵(lì)頻率推定系統(tǒng)的共振頻率。只要得到共振時(shí)的激勵(lì)頻率,就能得到系統(tǒng)的共振頻率。可用以下方法來得出共振時(shí)的激勵(lì)頻率。
電動(dòng)空壓機(jī)系統(tǒng)在取掉皮帶后,空壓機(jī)不工作,振動(dòng)系統(tǒng)的激勵(lì)來自電動(dòng)機(jī)轉(zhuǎn)子旋轉(zhuǎn),并與轉(zhuǎn)子的轉(zhuǎn)速相關(guān)。接通電源電動(dòng)機(jī)空轉(zhuǎn)時(shí),系統(tǒng)無共振;電動(dòng)機(jī)在減速后的高速區(qū)段系統(tǒng)出現(xiàn)共振:可以推定系統(tǒng)的共振頻率低于電動(dòng)機(jī)空轉(zhuǎn)頻率;該電動(dòng)機(jī)為三相異步電動(dòng)機(jī),源頻率為50 H z,其同步轉(zhuǎn)速為1 480 r/min(即24.67 H z),在電動(dòng)機(jī)空載時(shí)其轉(zhuǎn)速接近1 480 r/min,因此,可以推定系統(tǒng)的激勵(lì)頻率小于24.67 Hz。
電動(dòng)機(jī)帶動(dòng)空壓機(jī)運(yùn)行時(shí)系統(tǒng)的激勵(lì)來自電動(dòng)機(jī)和空壓機(jī)。空壓機(jī)空載運(yùn)行時(shí)電動(dòng)機(jī)的轉(zhuǎn)速比空壓機(jī)打風(fēng)時(shí)的轉(zhuǎn)速高,而空壓機(jī)空載時(shí)系統(tǒng)的振動(dòng)幅度有所減小,進(jìn)一步印證了空壓機(jī)正常工作時(shí)出現(xiàn)共振。該電動(dòng)空壓機(jī)正常工作時(shí)電機(jī)的轉(zhuǎn)速為1 450 r/min,由此可以推定該系統(tǒng)激勵(lì)頻率約為24.17 Hz(1 450/60)。得到系統(tǒng)共振的激勵(lì)頻率,也就得到系統(tǒng)的共振頻率。
使用有限元法也可求出系統(tǒng)的共振頻率。如果計(jì)算結(jié)果與以上結(jié)論一致,便可確認(rèn)該電動(dòng)空壓機(jī)異常振動(dòng)的原因,為徹底解決該問題提供幫助。
2.3 電動(dòng)空壓機(jī)的有限元分析
使用模態(tài)分析可以得到系統(tǒng)的各階模態(tài)和相應(yīng)振型,在設(shè)計(jì)時(shí)避免系統(tǒng)共振。模態(tài)分析有自由模態(tài)分析和約束模態(tài)分析。因該電動(dòng)空壓機(jī)的約束明確,故采用約束模態(tài)分析。
電動(dòng)機(jī)實(shí)際質(zhì)量為45 kg,三維建模時(shí)做成與實(shí)際體積近似的質(zhì)量塊;空壓機(jī)按照質(zhì)量65 kg三維建模時(shí)做成與實(shí)際體積近似的質(zhì)量塊;將吊架及吊架與車架的連接梁按照實(shí)際尺寸建模,并作適當(dāng)?shù)暮?jiǎn)化。
網(wǎng)格劃分,結(jié)構(gòu)分析對(duì)網(wǎng)格質(zhì)量要求不是很高,通常采用自動(dòng)網(wǎng)格劃分。網(wǎng)格質(zhì)量使用Skewness指標(biāo)。通常Skewness的平均值:對(duì)六面體、三角形和四邊形,應(yīng)小于0.8;對(duì)四面體應(yīng)小于0.9。使用ANASYS進(jìn)行網(wǎng)格劃分,其簡(jiǎn)圖如圖3所示。
圖3 電動(dòng)空壓機(jī)裝置三維模型網(wǎng)格劃分簡(jiǎn)圖
以吊架與車架主梁連接部分的剛性約束作為邊界條件,使用ANASYS進(jìn)行模態(tài)分析,其邊界條件簡(jiǎn)圖如圖4所示。
圖4 電動(dòng)空壓機(jī)裝置邊界條件簡(jiǎn)圖
使用ANASYS進(jìn)行模態(tài)分析,其6階模態(tài)和相應(yīng)振型如表1所示。
從表1可知:電動(dòng)空壓機(jī)的1階模態(tài)的頻率為21.027 Hz,振型為橫向振動(dòng)。1階模態(tài)屬于主振動(dòng),其振型與電動(dòng)空壓機(jī)的異常方向一致,可用作異常振動(dòng)的原因分析。
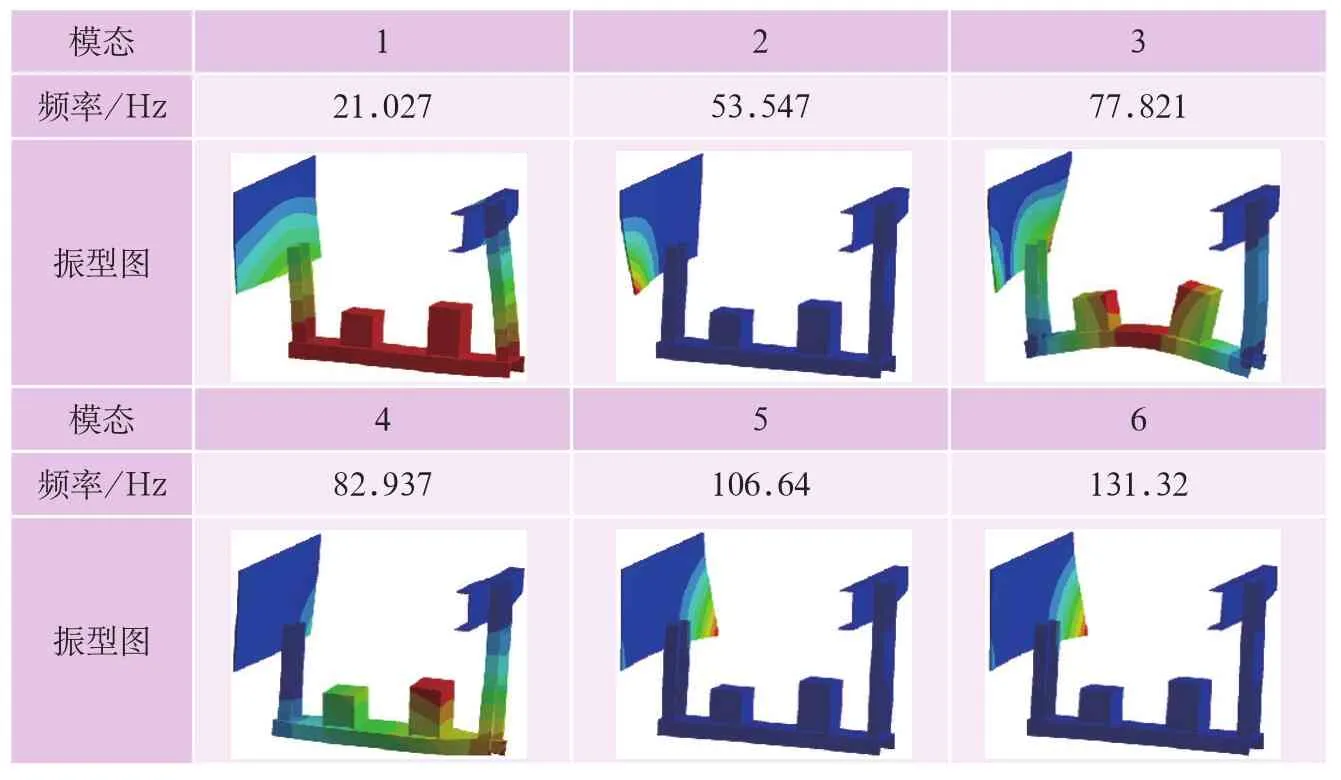
表1 電動(dòng)空壓機(jī)6階模態(tài)及其振型圖
2.4 電動(dòng)空壓機(jī)異常振動(dòng)的綜合分析
通過電動(dòng)空壓機(jī)振動(dòng)問題排查及試驗(yàn)分析得知:電動(dòng)空壓機(jī)在電動(dòng)機(jī)轉(zhuǎn)動(dòng)時(shí)因旋轉(zhuǎn)部件的轉(zhuǎn)動(dòng)不平衡產(chǎn)生周期性的作用力,這個(gè)作用力頻率接近24 Hz,將此看作激勵(lì)頻率;通過有限元計(jì)算得知,電動(dòng)空壓機(jī)的1階模態(tài)頻率為21.03 Hz,將此看作系統(tǒng)固有頻率。激勵(lì)頻率與系統(tǒng)固有頻率比值為1.14(24/21.03),這個(gè)值大于0.707(1/21/2)且小于1.414(21/2),頻率比接近1;電動(dòng)空壓機(jī)異常振動(dòng)方向?yàn)闄M向振動(dòng),與有限元計(jì)算的1階模態(tài)振型一致。基于以上兩點(diǎn)可得出結(jié)論:電動(dòng)空壓機(jī)振動(dòng)原因?yàn)橄到y(tǒng)共振。
3 電動(dòng)空壓機(jī)異常振動(dòng)的解決方法
系統(tǒng)共振問題可從改變系統(tǒng)的輸入頻率與固有頻率的比值入手,也可通過增加阻尼或隔離振源的方法入手。對(duì)電動(dòng)空壓機(jī)來說,改變系統(tǒng)固有頻率的方法最簡(jiǎn)單,成本最低。通過改變空壓機(jī)吊架及連接的剛度,使激勵(lì)頻率與系統(tǒng)固有頻率比值大于1.414或小于0.707,便可解決共振問題。
通過剛度分析得知:此空壓機(jī)的吊架與軌道車主梁的連接剛度較小。提高空壓機(jī)吊架與主梁的連接剛度可提高空壓機(jī)裝置的固有頻率;為安全起見,將空壓機(jī)的吊架一并加強(qiáng)。提高空壓機(jī)吊架與主梁的連接剛度方法是:①將主梁上的空壓機(jī)安裝橫梁加強(qiáng),如圖5所示,在空壓機(jī)橫梁上增加蓋板,使其截面由“[”形變?yōu)椤啊酢毙危黾涌古偠龋虎谠谲壍儡囍髁荷系目諌簷C(jī)安裝豎梁上增加筋板(圖5中筋板4),增加其抗彎剛度。提高空壓機(jī)吊架的方法是在空壓機(jī)吊架上增加筋板(圖5中筋板1、2、3)。
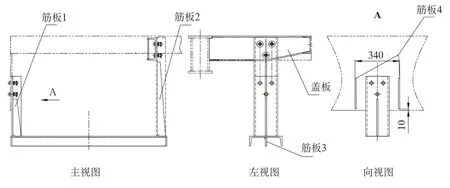
圖5 改進(jìn)后的電動(dòng)空壓機(jī)裝置(單位:mm)
為驗(yàn)證改進(jìn)方案的有效性,再次進(jìn)行模態(tài)分析。按照變更后的結(jié)構(gòu)建立三維模型,將三維模型輸入ANSYS進(jìn)行模態(tài)分析。其網(wǎng)格劃分簡(jiǎn)圖如圖6所示,其ANSYS分析的6階模態(tài)及其振型圖如表2所示。

圖6 改進(jìn)后的電動(dòng)空壓機(jī)三維模型網(wǎng)格劃分簡(jiǎn)圖
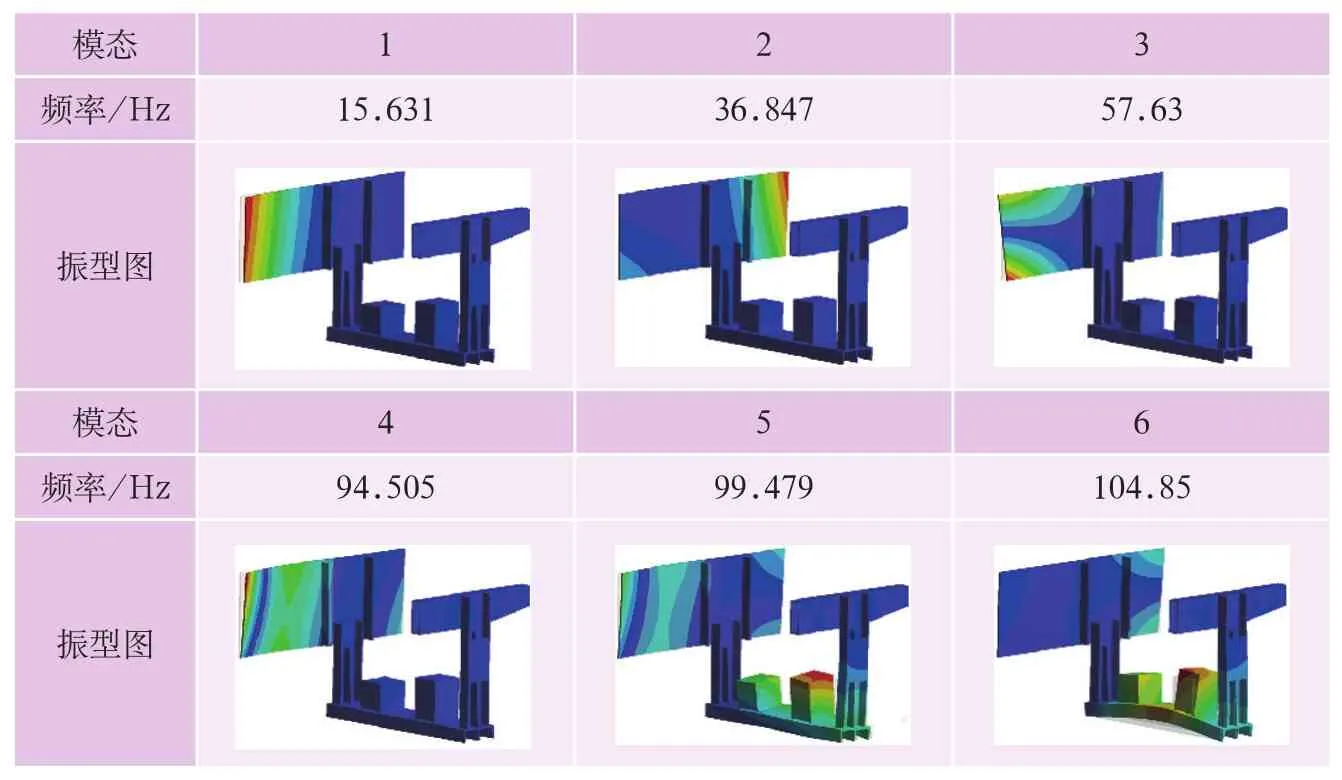
表2 改進(jìn)后的電動(dòng)空壓機(jī)6階模態(tài)及其振型圖
因其1、2、3、4階模態(tài)的振型為局部振動(dòng),與空壓機(jī)振動(dòng)無關(guān),不能作為分析依據(jù)。5階模態(tài)為系統(tǒng)固有頻率,振型與空壓機(jī)振動(dòng)一致,可作為分析依據(jù)。此時(shí)激勵(lì)頻率與系統(tǒng)固有頻率比值為0.24(24/99.479),且小于0.707(1/1.414)的頻率比,滿足防止共振的設(shè)計(jì)要求。
上述改進(jìn)方案經(jīng)過實(shí)際驗(yàn)證,沒有出現(xiàn)異常振動(dòng),效果良好,解決了該電動(dòng)空壓機(jī)異常振動(dòng)的問題。
4 結(jié)論
通過對(duì)軌道車電動(dòng)空壓機(jī)異常振動(dòng)的分析,并用有限元模擬分析進(jìn)行了對(duì)比,驗(yàn)證了異常振動(dòng)的原因。通過改變電動(dòng)空壓機(jī)的結(jié)構(gòu)和強(qiáng)度,從而改變其固有頻率,防止出現(xiàn)共振現(xiàn)象。經(jīng)過仿真模擬獲知,改進(jìn)后的電動(dòng)空壓機(jī)的固有頻率遠(yuǎn)離其激勵(lì)頻率,因此,確定了解決異常振動(dòng)的方案。最后經(jīng)過實(shí)際驗(yàn)證,改進(jìn)后的結(jié)構(gòu)沒有出現(xiàn)明顯的振動(dòng)現(xiàn)象。因此,整個(gè)分析、試驗(yàn)、論證及最后設(shè)計(jì)改進(jìn)是成功的,該方法可以有效地解決同類問題,同時(shí)對(duì)新產(chǎn)品的設(shè)計(jì)、優(yōu)化以及研發(fā)具有重要的指導(dǎo)意義。
[1] W Soedel. DESIGN AND MECHANICS OF COMPRESSOR VALVE [M]. 陜西西安:西安交通大學(xué)出版社,1986.
[2] 程耀東,李培玉. 機(jī)械振動(dòng)學(xué)(線性系統(tǒng))[M]. 浙江杭州:浙江大學(xué)出版社,1988.
[3] 尤詳勝. 往復(fù)式空氣壓縮機(jī)振動(dòng)故障診斷[J]. 壓縮機(jī)技術(shù),2006(4):19-23.
[4] 段進(jìn),倪棟,王國(guó)業(yè). ANSYS10.0結(jié)構(gòu)分析從入門到精通[M]. 北京:兵器工業(yè)出版社,2006.
責(zé)任編輯 冒一平
Analysis and Improvement of Vibration of Electric Air Compressor for Heavy Rail Vehicle
Zhang Bingqi
Abnormal vibration of a few electric air compressors in the air brake system occurs on a heavy rail vehicle. The testing method is used to get excitation frequency in the electric compressor. By using finite element method, the resonance frequency of electric air compressor is obtained. The structure of electric air compressor is changed, and by using finite element method the improved scheme is calculated and system-wide resonance is properly avoided. Through the actual verification, it is found that the abnormal vibration of the electric air compressor disappears, and the problem is solved completely.
electric air compressor, abnormal vibration, resonance, finite element calculation
U260.35+1
2015-03-31
張兵奇:寶雞南車時(shí)代工程機(jī)械有限公司,工程師,陜西寶雞 721000

