盾構隧道近距離平行穿越原水管道沉降分析
王培利 雷震宇 周 駿
盾構隧道近距離平行穿越原水管道沉降分析
王培利 雷震宇 周 駿
地鐵盾構推進過程中會對隧道周圍建(構)筑物和土層造成不同程度的影響。文章以上海軌道交通8號線某區間盾構隧道穿越既有原水管道為工程背景,應用ABAQUS有限元三維數值方法,分析盾構穿越既有原水管道時的原水管道沉降變形特征,分析不同施工參數對原水管道沉降的影響,并對既有原水管道沉降變形進行現場監測分析。計算和實測結果均表明原水管道沉降滿足《上海市原水引水管渠保護辦法》的規定要求。
盾構隧道;下穿原水管道;管線沉降
盾構隧道施工打破了地下管線周圍土體原有的力學平衡,帶動鄰近地下管線一同移動,致使管線產生一定程度的附加變形與附加應力。文獻[1]詳細敘述了盾構法隧道的施工過程、反應施工質量的等代層模擬方法,文獻[2]給出了在盾構開挖前地應力的平衡過程。文獻[5]采用數值計算方法,按管隧垂直、管隧平行2種情形,較為詳細地分析了土質、管線的直徑、壁厚、截面形狀、材質、管隧垂直間距、管隧水平間距等因素對地下管線的影響規律。本文采用三維有限元方法,建立符合實際工程特征的三維模型,模擬盾構推進的各種工況及施工因素(包括成層土、注漿等)的相互作用,分析上海軌道交通8號線某區間盾構穿越既有原水管道時對原水管道沉降的影響。
1 工程概況
上海軌道交通8號線某區間盾構隧道穿越既有Φ1.8 m原水管道,主要影響里程為XK30+735~XK30+935。隧道主要穿越的土層為灰色淤泥質粘土層,該層土呈流塑狀態,強度低、壓縮性高、滲透性弱、分布均勻,是上海地區盾構推進較為有利的土層(圖1)。主要土層土力學性質見表1。
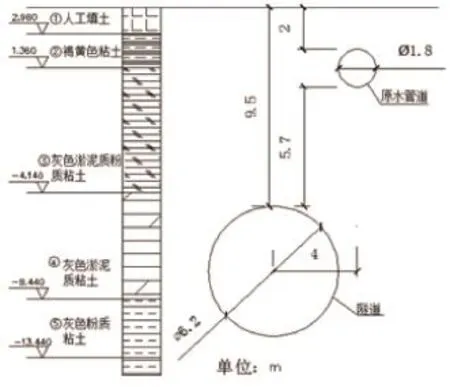
圖1 原水管道與下行線盾構隧道位置關系
2 有限元模擬分析
2.1 模型建立
首先,用ABAQUS/CAE建立土體、原水管道和襯砌、等代層模型,X為寬度方向,Y為深度方向,Z向為盾構掘進方向。本文選取三維有限元土體模型為200 m×60 m×30 m(依次為盾構掘進方向Z、寬度X和深度Y)。取土體本構模型為線性Drucker-Prager模型,混凝土襯砌和鋼管為彈性材料。襯砌管片為C55、S10鋼筋混凝土,尺寸為外徑6.2 m,厚度0.35 m,長度1.2 m;原水管道尺寸為外徑1.8 m,厚度0.1 m(圖2)。
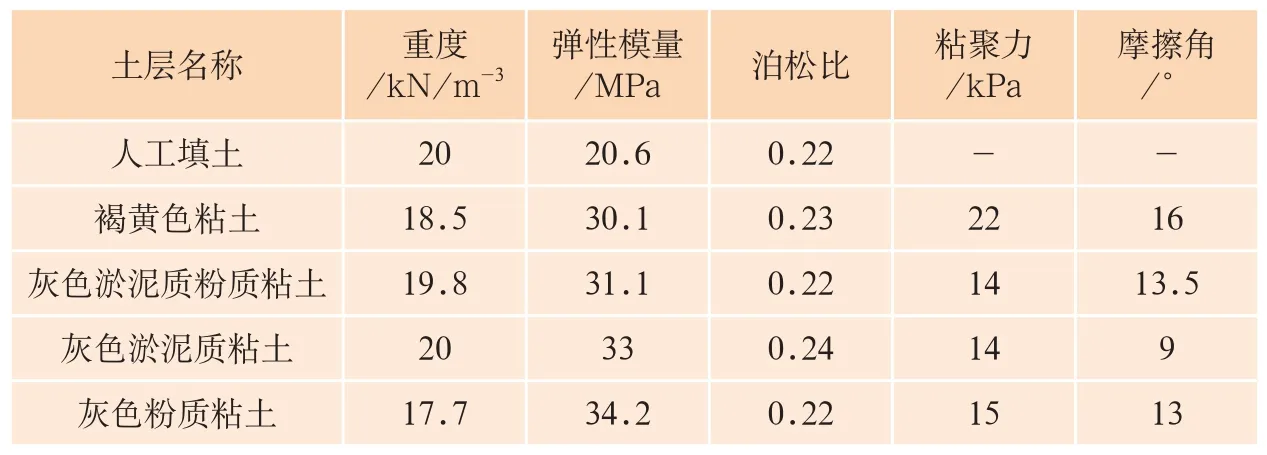
表1 主要土層土力學性質表

圖2 三維有限元模型圖
2.2 模型參數選取
在影響圍巖穩定性的各因素中,土體及襯砌材料的力學性質可通過試驗測定,難以確定的是盾尾空隙、土體向盾尾空隙的自然填充及注漿后漿體的分布情況和隧道壁面受擾動的程度和范圍。在實際施工中,要對它們分別進行量化是難以達到的,為此,將它們概化為一勻質、等厚、彈性的等代層,等代層的厚度δ可取為:

式(1)中, Δ為盾尾空隙的理論值,包括超開挖間隙、盾構殼厚度對應間隙以及操作間隙;η為折減系數,取值范圍為0.7~2.0,對于硬土層取下限,對極軟的土層取上限。上海地區為極軟土層,η取2.0。
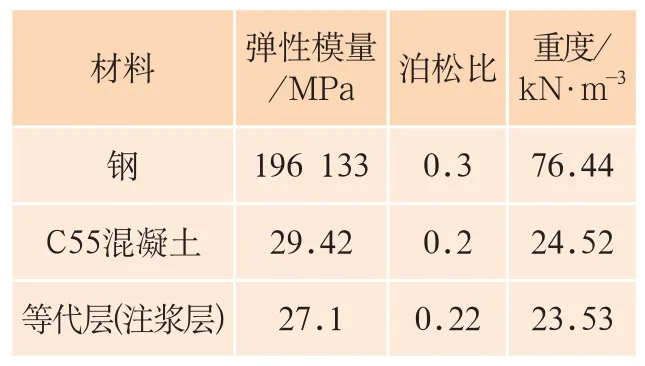
表2 盾構推進模擬參數表
表2給出了鋼管道、混凝土、等代層等盾構推進模擬參數。
2.3 地應力平衡
在模擬基坑開挖、隧道開挖、工后沉降、樁土復合地基、擋土墻等工程問題中,都需要平衡初始地應力,以最終得到既滿足平衡條件又不違背屈服準則的初始應力場,并保證各節點的初始位移近似為0。
2.4 盾構掘進模擬
盾構掘進過程模擬如下:
(1)在地應力平衡后,把原水管道實體解除鎖死,恢復原始的模型狀態;
(2)在盾構機開始掘進之前,盾構機對開挖面土體有頂推力F(面荷載),頂推力F按式(2)計算:

式(2)中, γ0為被移除土體重度 ( 本例取1 980 kN/ m3);h為土體深度 ( 本例為8.86~15.34 m);K0為土體側壓力系數 ( 本例取0.22);λ為擾動系數 ( 根據計算情況調整而定);
(3)在此分析步驟中,移除第1個開挖土體單元(長2 m),并相應激活等長度的等代層和襯砌;
(4)由于盾構機掘進對前方土體的擾動,分析步驟中相應衰減下一個即將被移除土體的彈性模量,即,將被移除的土體彈性模量衰減30%;
(5)按前4步的步驟如此循環,直至200 m長的土體被全部開挖,并完成隧道支護。
2.5 模擬結果分析
本次模擬盾構隧道平行穿越原水管道1次掘進2 m,并激活相應的襯砌和等代層(注漿層)。Z向為盾構掘進方向和原水管道縱向,Y向為垂直位移方向,正值為隆起,負值為沉降,并設定初始開挖面為Z=0 m,終止開挖面為Z=200 m。
2.5.1 原水管道縱向沉降分析
為揭示不同掘進程度對原水管道縱向沉降的影響,同時考慮規避模型邊界約束的影響,模擬計算中選取開挖面位置為Z=30、60、90、120、150、180 m時的原水管道縱向沉降,計算結果分別見圖3~8,由圖3~8可見:
(1)當盾構隧道掘進到Z=30 m時,原水管道在Z=0 m處的沉降為1.44 mm,并沿著盾構掘進方向逐漸增大,在Z=15 m處達到最大,為1.55 mm,然后沉降逐漸減小,直至距離開挖面后30 m處(即Z=60 m)之后,沉降接近0(圖3);
(2)當盾構隧道掘進到Z=60 m時,原水管道在Z=0 m處的沉降為1.44 mm,并沿著盾構掘進方向逐漸增大,在Z=40 m處達到最大,為2.39 mm,然后沉降逐漸減小,直至距離開挖面后30 m處(即Z=90 m)之后,沉降接近0(圖4);
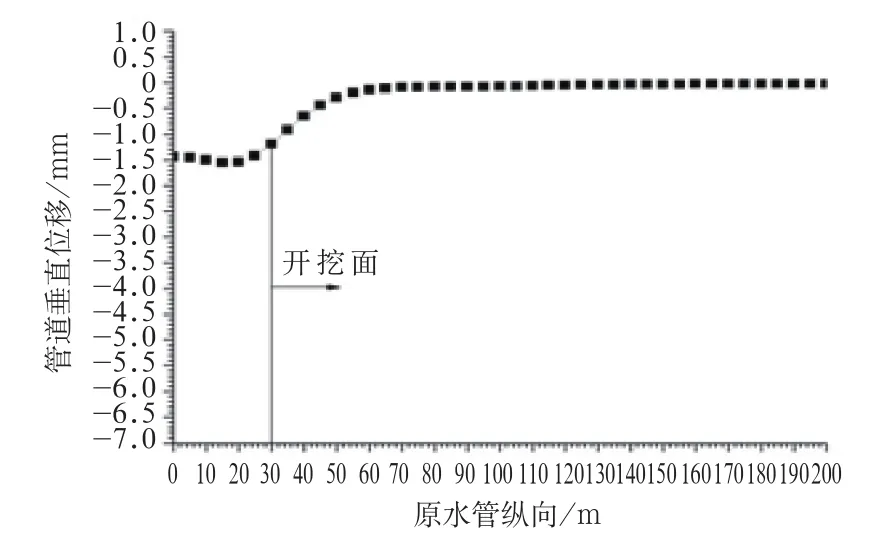
圖3 開挖面Z=30 m時原水管道管沉降曲線

圖4 開挖面位置Z=60 m時原水管道管沉降曲線
(3)當盾構隧道掘進到Z=90 m時,原水管道在Z=0 m處的沉降為1.63 mm,并沿著盾構掘進方向逐漸增大,并在Z=60 m處達到最大,為2.57 mm,然后沉降逐漸減小,直至距離開挖面后30 m處(即Z=120 m)之后,垂直位移接近0(圖5);
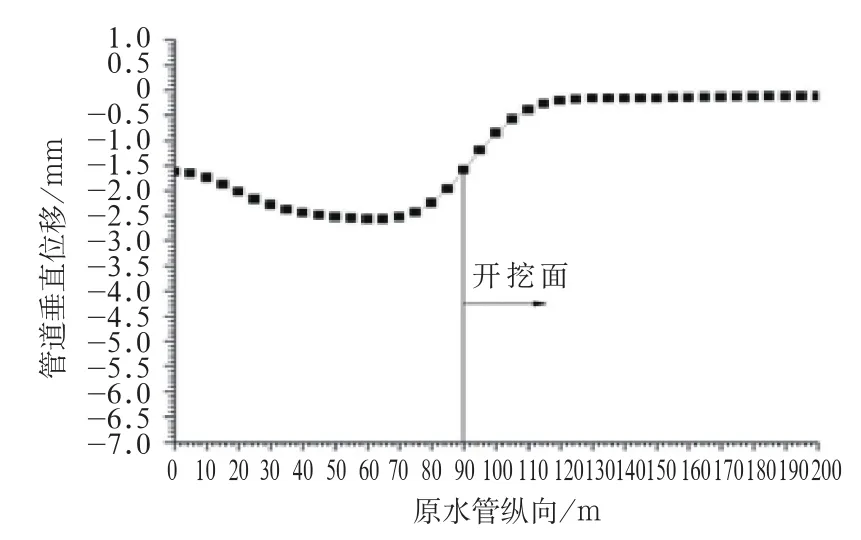
圖5 開挖面位置Z=90 m時原水管道管沉降曲線
(4)當盾構隧道掘進到Z=120 m時,原水管道在Z=0 m處的沉降為1.75 mm,并沿著盾構掘進方向逐漸增大,在Z=50 m處達到最大,為2.6 mm,在Z=50 m至Z=95 m這一段沉降幾乎保持不變,然后沉降逐漸減小,直至距離開挖面后30 m處(即Z=150 m)之后,沉降接近0(圖6);
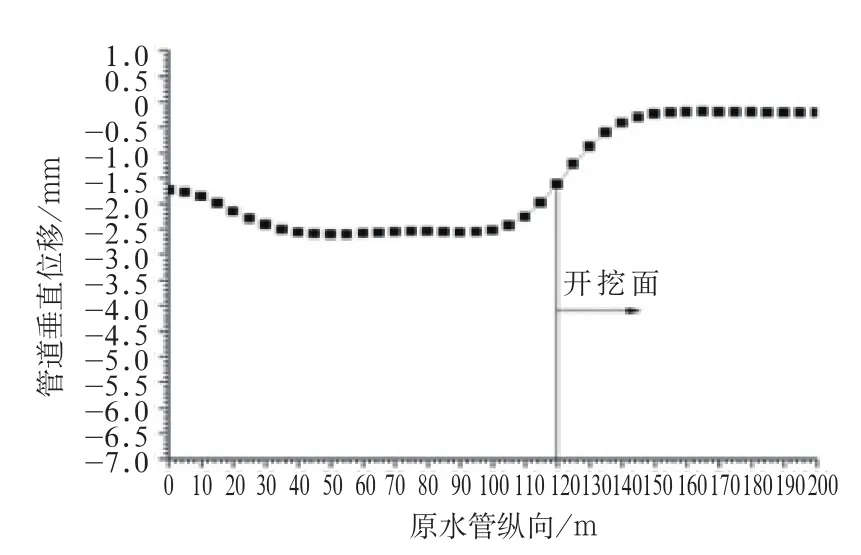
圖6 開挖面位置Z=120 m時原水管道管沉降曲線
(5)當盾構隧道掘進到Z=150 m時,原水管道在Z=0 m處的沉降為1.81 mm,并沿著盾構掘進方向逐漸增大,在Z=50 m處達到最大,為2.7 mm,在Z=50 m至Z=135 m這一段沉降幾乎保持不變,然后沉降逐漸減小,直至距離開挖面后30 m處(即Z=180 m)之后,沉降接近0(圖7);
(6)當盾構隧道掘進到Z=180 m時,原水管道在Z=0 m處的沉降為1.86 mm,并沿著盾構掘進方向逐漸增大,在Z=50 m處達到最大,為2.78 mm,在Z=50 m至Z=160 m這一段沉降幾乎保持不變,然后沉降逐漸減小,直至Z=200 m處沉降為0.8 mm(圖8)。
2.5.2 不同注漿量對沉降的影響
為計算分析施工中不同注漿量對原水管道沉降的影響,模擬計算中施工過程中,合適的注漿量按3.7 m3/環計算,不足注漿量按3 m3/環計算,在計算上以減小等代層模量(0.1倍)的方法來模擬。
圖9給出了開挖面位置Z=200 m時不同注漿量對原水管道沉降的影響曲線,由圖9可以看出,不同注漿量對原水管道沉降量影響較大,注漿量為3.7 m3/環時的原水管道沉降量較注漿量為3 m3/環時的原水管道沉降量降低約3.5 mm。可見,在盾構掘進過程中采取同步注漿和二次注漿的方法,可有效減少原水管道沉降量。
3 施工監測
3.1 監測點布置
根據現場實際情況,本監測在原水管道之上布置測點,以觀測原水管道沉降變化。考慮施工和原水管的安全,在施工段兩側的原水管道各延伸20 m進行布點。由于在盾構掘進到下行線390~430環與480~520環(共96 m),對原水管道影響較大,故對該區段進行重點監測,適當增加測點數,該區段的測點按6 m間距布設,其余段按12 m間距布設,測點總數為40個。具體布點情況參見圖10。

圖7 開挖面位置Z=150 m時原水管道管沉降曲線
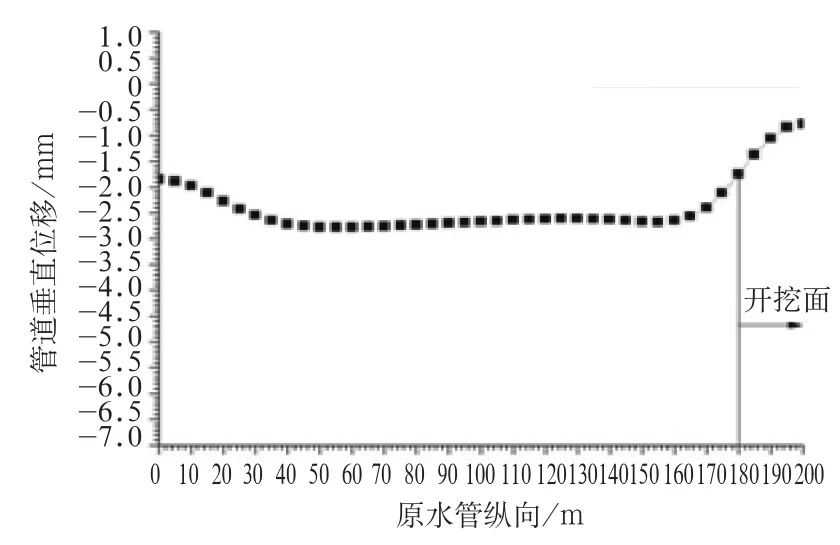
圖8 開挖面位置Z=180 m時原水管道管沉降曲線
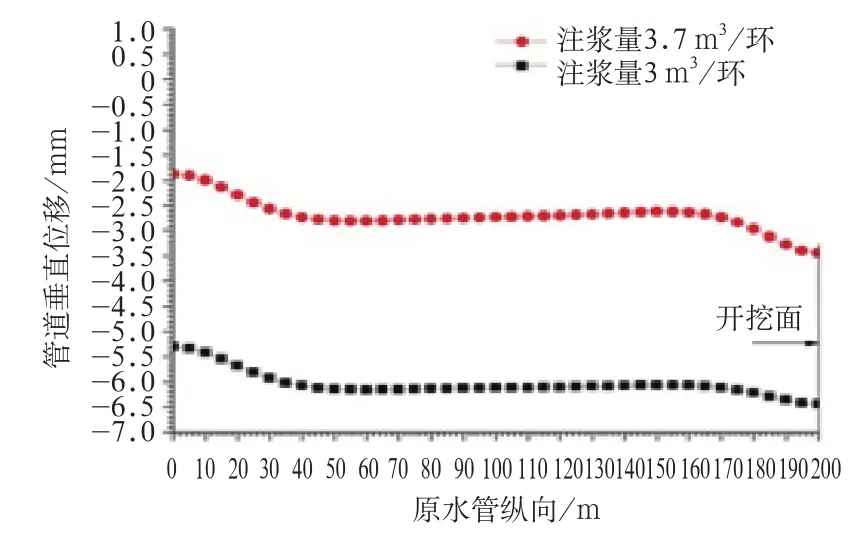
圖9 不同注漿量對原水管道沉降的影響

圖10 監測點布置
3.2 監測結果
在整個實際開挖過程中時,根據現場監測點的布點位置,選取盾構開挖面至Z=148 m和Z=188 m位置處時,測量原水管道沿縱向的實測沉降變化規律,見圖11、12。由圖11、12可見:
(1)當盾構掘進到Z=148 m時,原水管道在Z=0 m處的實測沉降值為1.35 mm,并沿著盾構掘進方向沉降在1~2 mm間變化,至原水管道Z=100 m后沉降逐漸增大,并在原水管道Z=145 m處達到最大,為2.8 m m,之后沉降逐漸減小,直至原水管道Z=200 m處沉降接近0(圖11);
(2)當盾構掘進到Z=188 m時,原水管道在Z=0 m處為的實測沉降值約為1.2 mm,并沿著盾構掘進方向實測沉降保持在1.2~1.4 mm之間,至原水管道Z=145 m后實測沉降逐漸增大,并在原水管道Z=180 m處達到最大,實測最大沉降值約為3.1 mm,之后實測沉降逐漸減小至原水管道Z=200 m處的2.6 mm(圖12);
4 結論
《上海市原水引水管渠保護辦法》規定“鋼管垂直方向附加變形≤0.01D”,對于本例,原水管道直徑為D=1.8 m,原水管道垂直向附加變形應≤18 mm。本文有限元模擬計算和現場實測原水管道最大沉降分別為2.78 mm和3.1 mm,模擬計算和實測結果均表明,盾構隧道穿越既有原水管道時,原水管道沉降滿足《上海市原水引水管渠保護辦法》的規定要求。
[1] 陳衛忠, 伍國軍, 賈善坡. ABAQUS在隧道及地下工程中的應用[M].北京:中國水利水電出版社, 2010.
[2] 曹金鳳, 石亦平. A BAQUS有限元分析常見問題解答[M]. 北京:機械工業出版社, 2010.
[3] 費康, 張建偉. ABAQUS在巖土工程中的應用[M]. 北京:中國水利水電出版社, 2010.
U456.3
王培利:同濟大學鐵道與城市軌道交通研究院,碩士研究生,上海 201804

