三維滲流數學模型在于橋水庫大壩滲流反饋計算中的應用
王立義,于艷秋
(天津市引灤工程于橋水庫管理處,天津301900)
三維滲流數學模型在于橋水庫大壩滲流反饋計算中的應用
王立義,于艷秋
(天津市引灤工程于橋水庫管理處,天津301900)
針對于橋水庫運行管理和安全監測揭示的問題,基于多組庫水位下的大壩滲流實測資料開展了蓄水現狀下大壩滲流場的三維有限元法反饋模擬計算,對蓄水現狀大壩滲流各部位的安全狀態進行了分析評價,反饋計算結果與監測資料分析和隱患探測成果一致,誤差控制在允許范圍,該結論為水庫大壩的滲透安全分析和高水位下滲流安全預報分析提供了有效的手段。
三維滲流數學模型;滲流反饋計算;水庫
1 問題提出
于橋水庫初建時,由于工期緊迫、技術和設備落后,加之冬季施工,壩基處理不徹底,致使大壩投入運行后出現很多問題,如壩肩、壩下及坡腳滲水、壩下滲壓過高、壩基測壓管水位超過地面、壩后出現沼澤化、冒水翻砂等問題。
針對此一系列問題,1976—1983年完成對壩基的第一次除險加固工程,之后分別于1995—1996、2001年對水庫大壩進行了加固處理。但仍有部分壩段的壩基滲壓過高,壩基非正常滲水仍然存在。
因此,筆者在進行現場地質鉆探試驗、隱患探測和觀測資料分析的基礎上,運用三維滲流數學模型進行大壩滲流反饋計算,對大壩存在的滲流問題進行安全評價,為水庫加固和安全運行提供了技術參考依據。
2 工程概況
于橋水庫位于天津薊縣城東4 km的薊運河左支流州河上,控制流域面積2 060 km2,總庫容15.59× 108m3,是一座以防洪、城市供水為主,兼顧農業灌溉、發電、水產養殖等綜合利用的大(1)型工程。該水庫大壩為均質土壩,最大壩高23.75 m(大沽高程,下同),壩頂高程28.30 m,壩長2 222 m,壩頂寬6 m,溢洪道底寬100 m,底高程18.5 m,泄洪能力4 138 m3/s,防洪標準為千年一遇,校核標準為萬年一遇。水庫蓄水庫容4.21×108m3(其中死庫容0.36×108m3,興利庫容3.85×108m3),防洪庫容12.62×108m3。2001年大壩進行防洪標準復核,正常蓄水位21.16 m,百年一遇設計水位24.60 m,千年一遇洪水位25.62 m,PMP校核洪水位27.72 m,死水位16.68 m。
3 滲流數學模型建立
三維滲流反演計算模型是以三維滲流有限元數值模型和觀測資料分析為基礎,在特定的地質環境條件下建立的。該模型充分利用已經取得的若干施工驗證資料和系統監測資料來反演各土層分布和計算參數以及防滲體系有效性,反饋分析水庫壩址區各種工況三維滲流場及其變化情況,重點反饋分析大壩滲水來源和壩基滲漏以及大壩整體滲流場分布特征。
3.1 滲流數學模型
符合達西定律的非均質各向異性不可壓縮土體的三維空間穩定滲流,其滲流域內任一點水頭函數應滿足下述基本方程式:
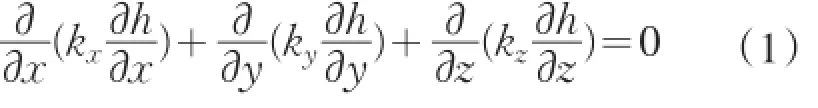
式中:h=h(x,y,z),為待求水頭函數;kx、ky、kz分別為x、y、z向滲透系數。
與式(1)相應的定解條件有水頭邊界和流量邊界。其中,水頭邊界公式為:
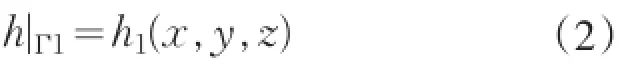
流量邊界公式為:
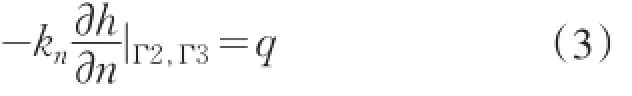
式中:邊界面Γ=Γ1+Γ2+Γ3。其中,Γ1為第一類邊界,如上、下游水位邊界,L由滲出段邊界等已知水頭邊界;Γ2為不透水邊界和潛流邊界等第二類邊界印已知流量邊界;Γ3為自由面邊界,在其上q= 0,自由面上任一點需滿足h*=z。
式(1)加上相應的初始條件和邊界條件式(2)、(3)就是摘述地下水滲流的數學模型。采用有限單元法,求解式(1)及相應定解條件。
本次滲流計算采用三維滲流計算程序UNSS3。計算中,土體透水性均概化為非均質各向同性,滲流量計算采用中斷面法。
3.2 模型建立與概化布置
根據基巖的分布情況,設定計算模型底部高程為-25 m、頂部高程為壩頂高程以及兩岸山體表面地形。兩岸邊界原則上分別為兩岸山體地下水分水嶺。其中,左岸地形較緩,遠離山體分水嶺以及溢洪道,邊界以樁號0+000處為界;右岸山體沿壩軸線至山體分水嶺,以此為界,如圖1所示。順州河向距壩軸線上、下游各取250 m,三維模型沿壩軸線方向劃分40個斷面,每個斷面上剖分結點數均為730個,剖分為對應的三角形單元;每個三角形單元與相鄰斷面上對應的三角形單元組成空間三棱柱單元,程序計算中自動將三棱柱單元剖分為3個四面體單元。總計劃分結點29 200個,四面體單元155 493個。計算網格充分考慮了大壩各土層分布和結構形式分布狀況及壩體、帷幕、防滲墻、排水體(表面溝、減壓溝)等建筑物的位置。
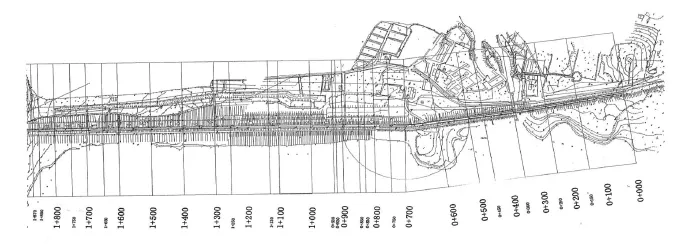
圖1 三維滲流計算模型剖分斷面和邊界
3.3 滲流計算參數反演
反演模型取用范圍基本上到達左右兩岸分水嶺位置,土層分層按實際大壩歷次地質勘探資料準確模擬,水工建筑物結構尺寸按實際尺寸模擬,未作簡化。因此,反演計算主要針對各土層滲透性的變化開展有限元法模擬計算,按照各斷面滲流監測孔實測資料進行對比驗證。各土層滲透性的初始數據主要依據大壩歷次地質鉆孔勘探、室內土工試驗、注水試驗以及注水試驗的結果選取。根據實際監測資料成果,結合工程經驗小范圍調整后,反演計算重新進行模擬計算分析,最終使得各孔滲流水頭計算值及大壩滲流量與實測值滿足一定精度要求。通過反演計算,最終得到各土層滲透系數。
4 滲流安全反饋計算分析
4.1 反饋模型建立
根據地勘資料及縱剖面圖的滲透分區,建立數值計算模型。模型范圍與上述相同,X向為壩軸線方向,Y向為垂直壩軸線方向,Z向為豎直方向。
4.2 反饋分析的模擬工況和計算參數
三維滲流計算邊界條件包括邊界地下水位、地表水位、地表出滲及特殊工況的內部邊界。反演水位選擇庫水位變化相對較為平緩的時段,進行反演模擬。本次計算選取1個月以上庫水位變化不大時,大壩滲流場為穩定滲流場。
本次計算模擬根據防洪復核的建議選取的特征水位如下:正常蓄水位21.16 m,相應下游水位9.80 m;設計洪水位25.62 m,相應下游水位9.80 m;校核洪水位27.72 m,相應下游水位9.80 m。
對運行庫水位進行蓄水運行反演分析,經迭代多次得到計算成果與監測資料擬合誤差最小的計算參數,由得到的反演模型來反饋大壩運行水位下的滲流安全性。
4.3 運行水位滲流反饋分析成果
通過對兩種工況下壩體和壩基各監測點實測值與計算值擬合對比,發現反演分析計算將運行水位下的各個監測孔計算值與實測值之間的擬合誤差控制在允許范圍內,本次反演模型能夠反映壩區滲流分布狀況。
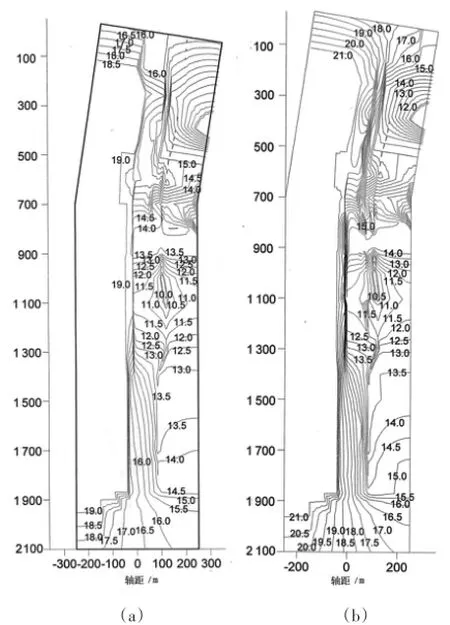
圖2 水位19.01、21.08 m壩體平面等水位分布
根據反演所得滲流參數進行計算,圖2(a)和(b)分別是工況1(19.01 m)、2(21.08 m)水位下的大壩壩體與壩基第一透水層頂板承壓水頭等水位線圖。
4.4 運行水位反饋分析評價
由運行水位下三維滲流場的反演變化情況可以知道大壩壩體和壩基滲流場分布特征。在反演計算模擬蓄水運行滲流場過程中,考慮了壩基各參數的各向異性,與實際滲流條件具有較好一致性。因此,模型概化和選用參數是合理的,可以應用該模型來預報正常蓄水位下的滲流場分布。
通過對壩體滲流場、壩基滲流場、大壩總體滲流量的分析,可以得出以下結論:壩基滲透是水庫滲漏的主要來源,壩基滲流為于橋水庫滲流的主要形式,壩基廣泛存在的沙礫石透水層即為滲流路徑。而右壩段的滲流量為全壩段最主要滲漏來源,一方面是因為此段存在未封閉的地下透水層,滲漏量較大;另一方面,高噴防滲墻未能達到預期效果,大壩浸潤線和滲流量未能有效降低。
5 結論
筆者建立三維滲流數學模型,對于橋水庫大壩各部位滲流進行反饋計算,反饋計算結果與監測資料分析和隱患探測成果一致,誤差控制在允許范圍,并通過對結果的分析得出水庫壩體與壩基滲透特征,為水庫大壩的滲透安全分析和高水位下滲流安全預報分析提供了有效的手段。
TV62+2;TV698.1+2
A
1004-7328(2015)05-0040-03
10.3969/j.issn.1004-7328.2015.05.014
2015-05-10
王立義(1973—),男,高級工程師,主要從事水利工程管理工作。

