基于輸入輸出數據的非線性系統建模
張 旭
(中國電子科技集團公司第二十研究所,陜西 西安 710068)
0 引言
線性系統建模方法雖然對于線性系統具有很好的效果。隨著控制過程要求的不斷提高,相對于一個線性模型在當前工作點的局部近似,非線性模型能更好地描述過程在整個運行過程的整體特性,在實際應用中具有很好的效果。模塊化非線性模型是一種非線性模塊與線性子系統的串聯型的模型,由于其結構清晰,并能描述常見的非線性系統,所以得到了廣泛地關注與應用[1-2]。
近年來,對于模塊化非線性Hammerstein 型的辨識文獻相對較多。Narendrad 等[3-4]提出了迭代方法,將參數化為線性模塊參數和非線性模塊參數兩個集合,計算一個參數集最優估計值時固定另一個,兩參數集估計輪換計算,但兩個參數集之間的鏈接矩陣是一個輸入變量的函數矩陣,由此導致迭代最小二乘法的協方差矩陣計算量大。Chang等[5]提出了過參數辨識方法,是把非線性展開為一些基函數的和,經參數化后得到一個過參數化模型,然而得到的模型參數向量包含了原始的靜態非線性模塊與線性模塊參數的乘積,使得參數向量維數大大增加,導致算法計算量相應增加。Pawlak[6]給出隨機方法,利用白噪聲性質分離線性部分與非線性部分。Bai 等[7-8]給出了分離最小二乘法、盲辨識和頻域辨識法。
為此,本文利用正交基辨識法對輸入非線性模型(Hammerstein-型)進行建模,其優點是避免了迭代算法以及參數向量維數增大所帶來的計算量,對于正交基函數的獲取進行改進,對輸入輸出數據做特殊處理,僅利用利用輸出信號恢復中間變量,最終利用最小二乘法得到模型參數,仿真結果表明了方法有效性。
1 輸入型非線性系統建模
1.1 輸入型非線性系統描述
Hammerstein 模型是一種輸入端具有非線性的串聯型非線性系統模型圖1 所示,被應用于許多工程問題中。考慮離散的Hammerstein型系統,建模的目的是僅基于輸入數據u 輸出數據y,估計線性部分的傳遞函數G(z)以及非線性函數f(u),其中間變量x 是不可測量的,預先設定線性部分的模型階數為n。

圖1 Hammerstein 模型
輸入端的非線性模塊,通常以泰勒展開多項式的形式進行描述,即

其中r 是非線性種多項式的個數,線性子系統可以通過輸出信號與中間變量的離散傳遞函數描述為
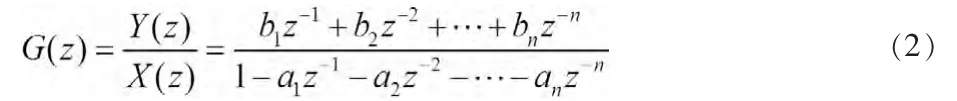
1.2 線性傳遞函數分母參數確定
首先對系統的輸入輸出信號進行特殊處理,根據系統的特點消除中間變量,利用最小二乘法估計出傳遞函數分母參數,具體方法描述如下:
輸入信號的采樣間隔為T,不在采樣點上的數據設置為零,對于輸出使用間隔h=T/(n+1)來進行采樣,如圖2、圖3 所示。

圖2 輸入數據采樣
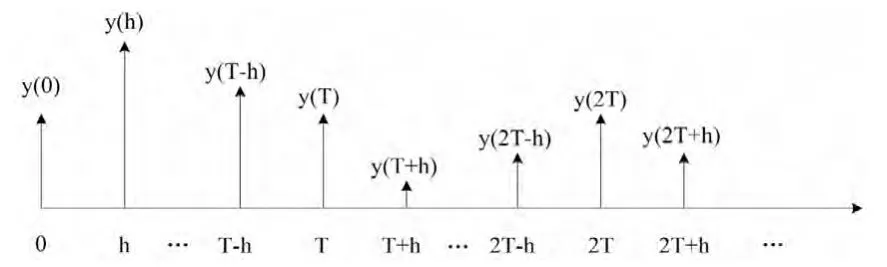
圖3 輸出數據采樣
將式(2)的線性模型轉換為時域表達式
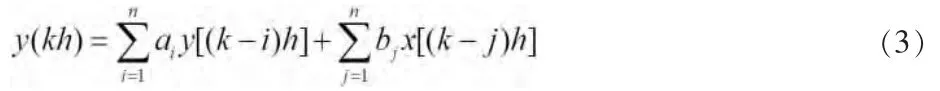
根據式(3)和圖2,可以看出只有當t=kT=k(n+1)h 時,x(t)才為非零值,而
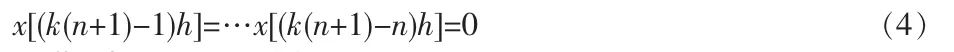
因此,當k=l(n+1)時有

在此定義矩陣
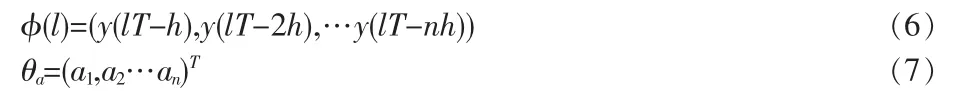
將式(6)和(7)代入式(5)可以得到矩陣的表示形式

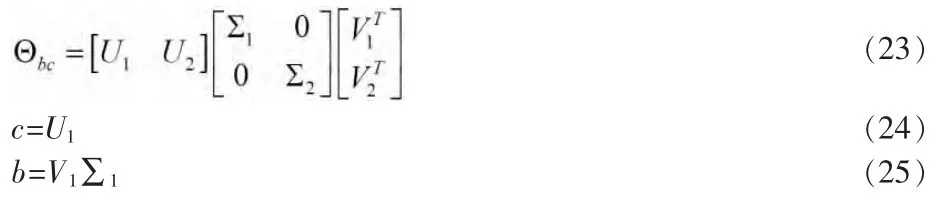
在計算分母參數時采用最小二乘法,本文采用最小二乘估計的算法來計算,構造以下矩陣
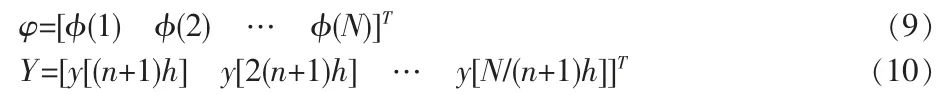
其中N 為輸出數據個數,通過式(9),(10),(11)得到如下矩陣

θa利用最小二乘估計可以得到

(φ)+是矩陣(φ)的廣義逆矩陣,以此通過上式便求得線性傳遞函數的分母多項式的參數。
1.3 線性傳遞函數分子與非線性參數的確定
傳統的正交基建模的方法,對于正交基函數的獲取是通過先驗知識或者相關的經驗,本文在求得線性部分傳遞函數分母的基礎上,可以求得傳遞函數的極點值,然后采用正交基辨識思想來利用極點構造標準正交基函數,將線性子系統表示為基函數的形式,結合非線性模塊表達形式構造出關系矩陣,最后利用奇異值分解的方法獲得各個模塊的參數,從而減少了對于先驗知識的依賴,并具有更高的準確性,具體描述如下所示:
參考圖1,對線性部分采用基函數的表達形式:

其中,p=n+1,Bl(z)是線性部分的正交基函數。根據正交基系統辨識的方法在這里對于線性模塊的基函數取做如下形式[9]
ξi是線性部分的極點,可以通過已經求的分母構造多項式進行求解得到。將tk時刻的輸入表示為uk,將線性子系統與非線性模型相結合通過式(2)和(14)可以將tk時刻輸出yk用如下的公式表示

觀察上面的式子,通過最小二乘法或其他算法進進行估計參數的時候得到的是bc 的形式,這也是所有的串聯模塊化非線性辨識的通病,結果經過分離后得到的參數往往是[αc,α-1b]的形式,其中α 為一常數,因為在分離兩者時沒有一個統一的標準,即前面有可能多乘了一個常數,后面少乘了個常數,但是整體的效果是一樣。這就要求有一個標準使得到的參數保持唯一性,大多方法都是使分子參數的二范數為1,這種參數的不唯一性對于整體系統的結果是不影響的。
構造矩陣
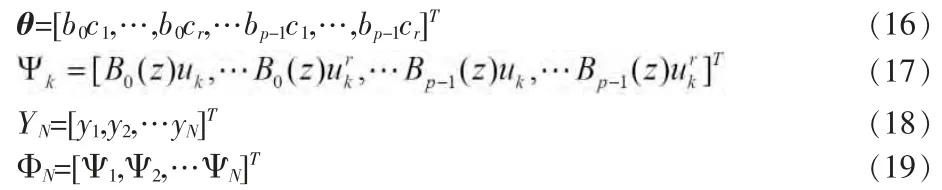
將式(18)和(19)代入式(15)得到

從(20)式利用最小二乘可以得到θ 估計

利用式(16)的形式來構造如下矩陣
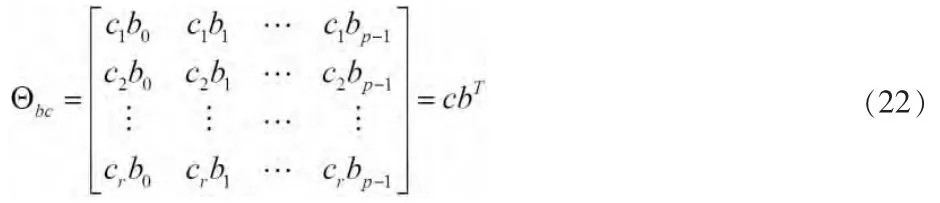
為了求b 和c,對式(22)的矩陣采用著名的奇異值分解的方法
2 系統仿真
假設線性部分離散傳遞函數為

輸入非線性模型為

對于上述模型進行辨識,輸入采用的是[-1 1]上均勻分布的脈沖序列,采樣時間0.015s,輸出的數據時間間隔為0.005s,數據的處理如圖2 和圖3;
通過章節1.2 得到線性部分傳遞函數的分母參數

通過線性部分的分母,可以得到傳遞函數的兩個極點,根據式(3-15)構造得到兩個正交基函數為

利用章節1.3 中正交辨識建模的方法來獲得線性傳遞函數的分子參數,與輸入非線性的模塊的參數。
給定系統參數與建模后得到模型參數對比如下表:
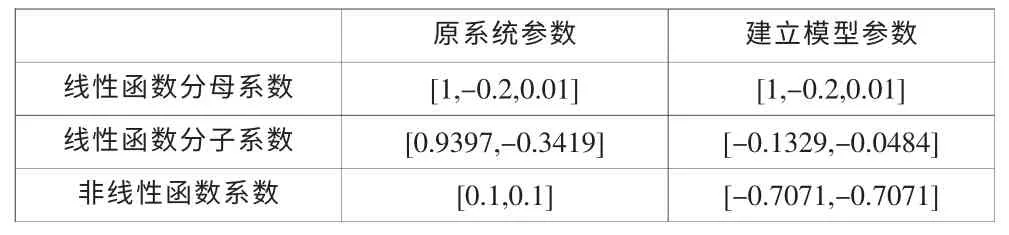
表1 Hammerstein-系統建模參數對比
雖然由于串聯型系統建模的通病使得各個模塊的擦參數在數值上有所不同,但是整體效果是一樣的,參數間會保持一定的比例的關系,建立模型的輸出和實際輸出結果如圖4 所示,兩者誤差如圖5 所示。
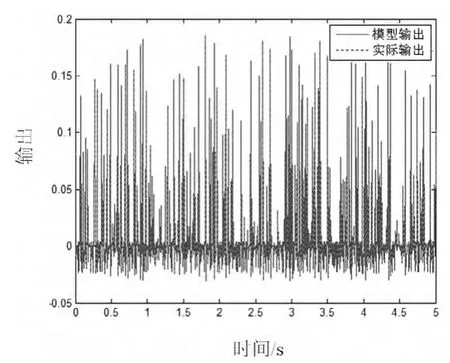
圖4 Hammerstein-型建模與實際系統輸出
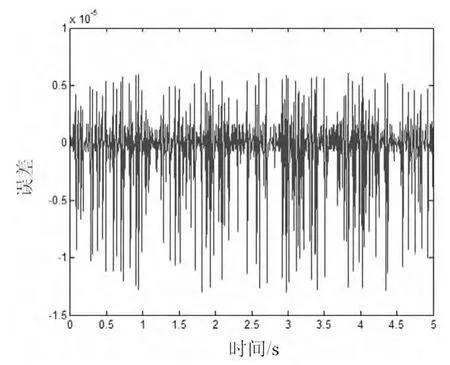
圖5 Hammerstein-型建模與實際系統輸出誤差
從圖4 和圖5 可以看出對于輸入非線性系統通過正交基辨識法建立的模型與實際系統輸出十分吻合,誤差數量級很小,說明模型能夠較好的描述系統,表明算法有效性。
3 結束語
本文研究了基于輸入輸出數據的模塊化非線性模型,對輸入非線性(Hammerstein-型)模型利用盲辨識建模算法進行建模,通過對輸入輸出數據進行不同間隔的采樣,僅利用測量的輸出數據來計算構造中間變量,并應用最小二乘估計各個模塊的參數。并對傳統的正交辨識算法中的正交基函數的的構造進行改進,這種方法與傳統方法相比減少經驗和先驗知識的依賴,而且具有更高的準確性。最后通過仿真實例的驗證,表明算法有效性。
[1]習毅,潘豐.基于Hammerstein 模型的非線性自適應預測函數控制[J].系統工程與電子技術,2008,30(11):2237-2240.
[2]Chang F,Luus R.A noniterative method for identification using Hammerstein model[J].IEEE Transactions on Automatic Control,1971,AC16:464-468.
[3]Narendra K S,Gallman P G.An iterative method for the identification of nonlinear systems using a Hammerstein mode[J].IEEE Transactions on Automatic Control,1966,AC-11:546-550.
[4]Voros J.Parameter identification of discontinuous Hammerstein systems[J].Automatic,1997,33(6):1141-1146.
[5]Chang F,Luus R.A noniterative method for identification using Hammerstein model[J].IEEE Transactions on Automatic Control,1971,AC-16-468.
[6]Pawlak M.On the series expansion approach to the identification of Hammerstein systems[J].IEEE Transactions on Automatic Control,1991,36(6):763-767.
[7]Bai E W.Identification of systems with hard input nonlinearities[C]//Perspectives in Control,Moheimani R.Ed.New York:Springer Verlag,2001.
[8]Bai E W,Fu M Y.A blind approach to Hammerstein model identification[J].IEEE Transactions on SignalProcessing,2002,50(7):1610-1619.
[9]B.Ninness and F.Gustafsson.A unifying construction of orthonormal-bases for system identification[J].IEEE.Trans.Automat.Contr.,AC-42(4):515-521,1997.

