淺議求解最短路徑問題的兩種算法
高 嵐
(吉林工程技術(shù)師范學(xué)院信息工程學(xué)院,吉林 長(zhǎng)春 130052)
0 引言
最短路徑問題是網(wǎng)絡(luò)分析中最基本的組合優(yōu)化問題之一,在公交路線網(wǎng)絡(luò)規(guī)劃中應(yīng)用廣泛。因此,實(shí)際公交線網(wǎng)優(yōu)化設(shè)計(jì)中,路徑選擇算法成為一個(gè)重要研究課題,它直接關(guān)系到交通網(wǎng)絡(luò)效率、傳輸延遲和吞吐量等主要技術(shù)性能指標(biāo)。
早在20世紀(jì)初,最短路徑這一重要問題就已得到人們的高度重視,當(dāng)時(shí)有許多科學(xué)家研究這一問題的求解方法,但直到1959年荷蘭計(jì)算機(jī)科學(xué)家Dijkstra(迪加斯特拉)才給出這一問題求解的基本思想,成為一代經(jīng)典。當(dāng)時(shí)的Dijkstra 提出的這一算法主要解決的是從固定的一點(diǎn)到其他各點(diǎn)的最短路徑問題。但實(shí)際生活中要求解的可能是任意兩點(diǎn)間的最短距離,可采用Floyd(弗洛伊德)算法。本文通過將兩種算法進(jìn)行一些對(duì)比討論,得出關(guān)于兩種算法效率和適用問題的一些結(jié)論。
1 最短路徑問題
最短路徑問題是圖論中的基本問題。在賦權(quán)圖中,找出兩點(diǎn)間總權(quán)和最小的路徑就是最短路徑問題。最短路徑算法包括指定頂點(diǎn)對(duì)之間的最短路徑算法和所有頂點(diǎn)間的最短路徑算法,前者對(duì)于運(yùn)輸?shù)暮侠砘哂兄匾碚撘饬x,而后者的意義在于選擇合理的中轉(zhuǎn)中心,使得總費(fèi)用最少。在圖論中最典型的兩種求最短路徑算法分別是Dijkstra 算法和Floyd 算法。
2 Dijkstra 算法
2.1 算法基本思想
每次新擴(kuò)展一個(gè)距離最短的點(diǎn),更新與其相鄰點(diǎn)間距離。當(dāng)所有邊的權(quán)都為正時(shí),由于不會(huì)存在一個(gè)距離更短的沒有擴(kuò)展過的點(diǎn),所以這個(gè)點(diǎn)的距離不會(huì)再被改變,因而保證了算法的正確性。根據(jù)這個(gè)原理,采用Dijkstra 算法求解最短路的圖不能有負(fù)權(quán)邊,因?yàn)閿U(kuò)展到負(fù)權(quán)邊的時(shí)候會(huì)產(chǎn)生更短的距離,有可能破壞已經(jīng)更新的點(diǎn)距離不會(huì)改變的性質(zhì)。
2.2 Dijkstra 算法思想在物流配送中的應(yīng)用
采用圖論中的最短路徑算法Dijkstra 算法來建立物流配送路徑選擇模型,主要思想是從代表兩個(gè)頂點(diǎn)的距離開始,每次插入一個(gè)頂點(diǎn)比較任意兩點(diǎn)之間的已知最短路徑和插入頂點(diǎn)作為中間頂點(diǎn)時(shí)兩點(diǎn)間的最短路徑,得到的最終的權(quán)矩陣就反映了所有頂點(diǎn)間的最短距離信息。最短距離者作為費(fèi)用最小者,即最佳的物流配送選址位置。
3 Floyd 算法
3.1 算法基本思想
通過一個(gè)圖的權(quán)值矩陣求出它的每?jī)牲c(diǎn)間的最短路徑矩陣。
從圖的帶權(quán)鄰接矩陣A=[a(i,j)]n×n 開始,遞歸地進(jìn)行n 次更新,即由矩陣D(0)=A,按一個(gè)公式,構(gòu)造出矩陣D(1);又用同樣地公式由D(1)構(gòu)造出D(2);……;最后又用同樣的公式由D(n-1)構(gòu)造出矩陣D(n)。矩陣D(n)的i 行j 列元素便是i 號(hào)頂點(diǎn)到j(luò) 號(hào)頂點(diǎn)的最短路徑長(zhǎng)度,稱D(n)為圖的距離矩陣,同時(shí)還可引入一個(gè)后繼節(jié)點(diǎn)矩陣path 來記錄兩點(diǎn)間的最短路徑。
3.2 Floyd 算法在選址問題中的應(yīng)用
某城市考慮建立區(qū)域內(nèi)二次供水中轉(zhuǎn)站。在選址問題中,點(diǎn)表示可供選址,其間連線表示運(yùn)輸費(fèi)用,其需求點(diǎn)之間運(yùn)費(fèi)如圖1 所示。在選址中,要求該中轉(zhuǎn)站到其他站點(diǎn)的距離最短,即運(yùn)輸費(fèi)用最少,通過運(yùn)用求解最短路徑的Floyd 算法可求出該網(wǎng)點(diǎn)布局的最佳中轉(zhuǎn)站。
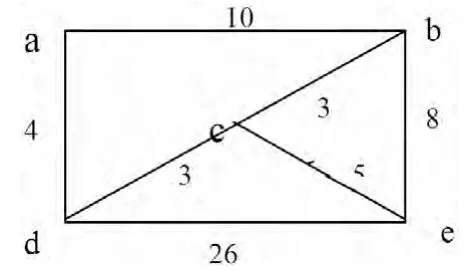
圖1 網(wǎng)絡(luò)拓?fù)?/p>
由計(jì)算可知,a 到其他點(diǎn)的費(fèi)用和為C(a)=33,同理C(b)=27,C(c)=18,C(d)=21,C(e)=33,比較可知c 到其他各點(diǎn)的費(fèi)用最小。因此本例從經(jīng)濟(jì)性考慮,選c 點(diǎn)為中轉(zhuǎn)站最優(yōu)。
4 討論
典型的最短路徑求解算法Dijkstra 算法和Floyd 算法各有所長(zhǎng)。Dijkstra 算法可為任一源節(jié)點(diǎn)找出與其它所有節(jié)點(diǎn)的最短路徑,是目前公認(rèn)的較好的最短路徑算法,但由于它遍歷計(jì)算的節(jié)點(diǎn)很多,所以效率低。Floyd 算法是一種用于尋找給定的加權(quán)圖中頂點(diǎn)間最短路徑的算法,是一種動(dòng)態(tài)規(guī)劃算法,可以算出任意兩個(gè)節(jié)點(diǎn)之間的最短距離,代碼編寫簡(jiǎn)單,但是Floyd 算法計(jì)算最短路徑時(shí)時(shí)間復(fù)雜比較高,不適合計(jì)算大量數(shù)據(jù)。
綜上,求解單源點(diǎn)無負(fù)權(quán)邊最短路徑可采用Dijkstra 算法,而求所有點(diǎn)最短路徑應(yīng)用Floyd 算法。對(duì)于稀疏圖,采用n 次Dijkstra 算法比較出色,對(duì)于稠密圖,適用Floyd 算法。
5 結(jié)束語
本文通過對(duì)比兩種求解最短路徑算法的設(shè)計(jì)思想、求解過程、應(yīng)用實(shí)例,討論了算法的特點(diǎn)及適用領(lǐng)域。了解算法求解問題的差異,針對(duì)不同類型問題采取對(duì)應(yīng)的求解算法,將大大提升解決問題的效率,對(duì)實(shí)際生產(chǎn)生活起到重要作用。
[1]辛建亭,胡萍.圖論在通訊網(wǎng)中的應(yīng)用[J].2009,3.
[2]凡金偉,呂康.基于Dijkstra 算法在物流配送中的應(yīng)用[J].電腦編程技巧與維護(hù),2009(4):39-45.
[3]鄧春燕.兩種最短路徑算法的比較[J].電腦知識(shí)與技術(shù),2008(12):511-512.
[4]徐鳳生.求最短路徑的新算法[J].計(jì)算機(jī)工程與科學(xué),2006,2.
[5]殷劍宏,吳開亞.圖論及其算法[M].合肥:中國(guó)科學(xué)技術(shù)大學(xué)出版社,2005.
[6]陳玉華.淺談圖論在現(xiàn)實(shí)生活中的應(yīng)用[J].云南省教育學(xué)院學(xué)報(bào),2004.
[7]王燕,蔣笑梅.配送中心全程規(guī)劃[M].北京:機(jī)械工業(yè)出版社,2004.
[8]項(xiàng)榮武,劉艷杰,胡忠盛.圖論中最短路徑問題的解法[J].沈陽航空工業(yè)學(xué)院學(xué)報(bào),2004.

