火力發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片根部形狀優(yōu)化設(shè)計(jì)

火力發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片根部形狀優(yōu)化設(shè)計(jì)

吳廣發(fā)

(聊城大學(xué)東昌學(xué)院機(jī)電工程系，山東 聊城 252000)

摘要：火力發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片是在高溫高壓環(huán)境中長(zhǎng)期高速旋轉(zhuǎn)工作，在離心力作用下，葉片根部的應(yīng)力集中現(xiàn)象非常嚴(yán)重，而這正是導(dǎo)致葉片失效的主要原因。為此，對(duì)火力發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片進(jìn)行優(yōu)化設(shè)計(jì)，經(jīng)優(yōu)化，葉片根部的最大米賽斯應(yīng)力從初始形狀時(shí)的56.97 kg/mm2降低到優(yōu)化形狀的49.15 kg/mm2，應(yīng)力降低幅度為13.73%。

關(guān)鍵詞：蒸汽汽輪機(jī)；葉片；優(yōu)化設(shè)計(jì)；米賽斯應(yīng)力

收稿日期：2015-07-27

作者簡(jiǎn)介：吳廣發(fā)(1983—)，男，山東聊城人，助教，研究方向：機(jī)械設(shè)計(jì)、機(jī)械優(yōu)化、有限元分析。

1輪機(jī)葉片根部?jī)?yōu)化問(wèn)題概述

火力發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片是在高溫高壓環(huán)境中長(zhǎng)期高速旋轉(zhuǎn)工作，在離心力作用下，葉片根部的應(yīng)力集中現(xiàn)象非常嚴(yán)重，而這正是導(dǎo)致葉片失效的主要原因。

為便于及時(shí)快速地更換失效葉片，發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片較多地采用如圖1所示的插入式組裝結(jié)構(gòu)。

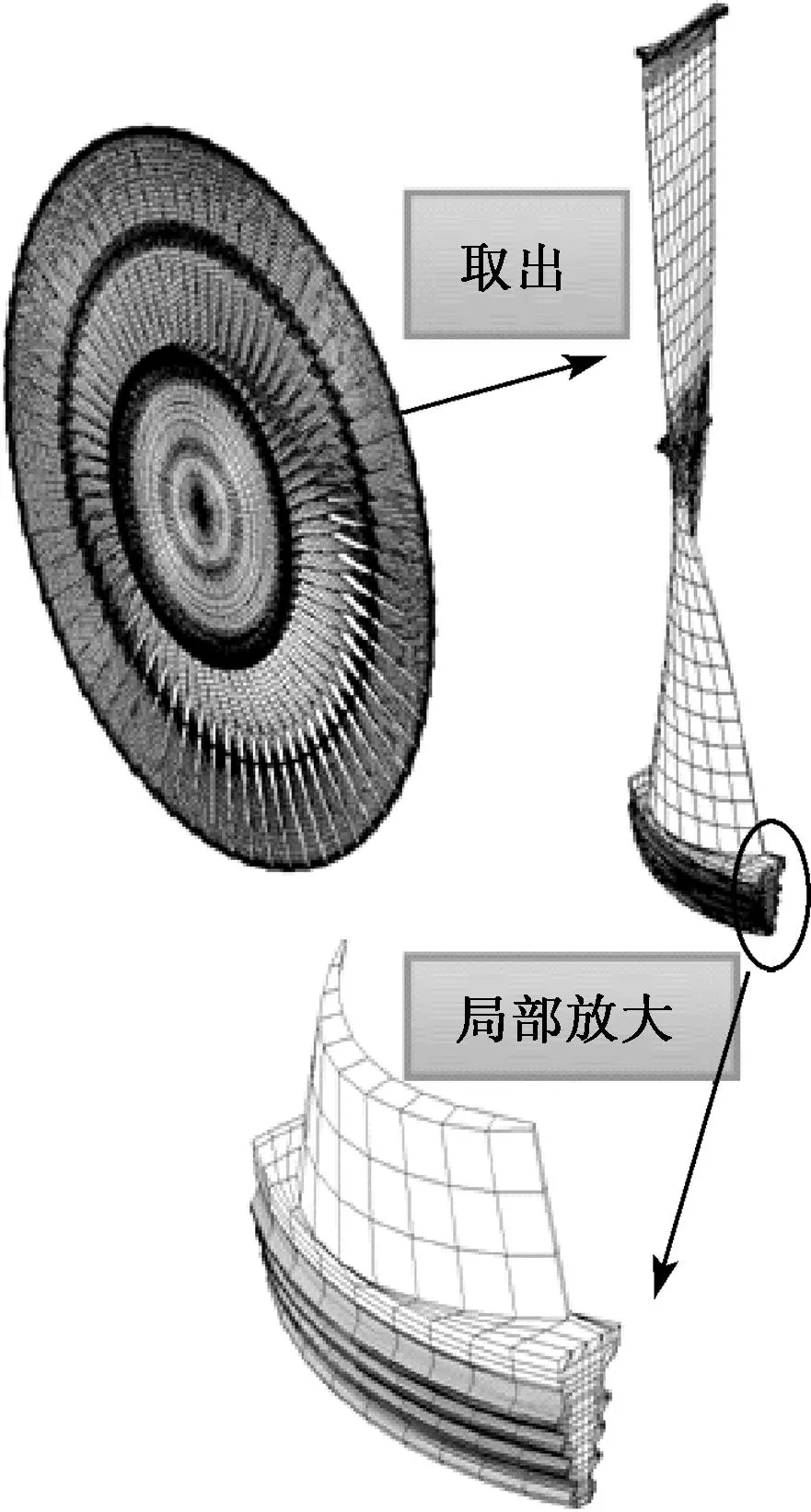
圖1　火力發(fā)電機(jī)組的蒸汽汽輪機(jī)葉片結(jié)構(gòu)簡(jiǎn)圖

2優(yōu)化計(jì)算過(guò)程

將葉片根部插入部分沿著葉片的抽出方向取出一個(gè)典型斷面，簡(jiǎn)化為平面應(yīng)變問(wèn)題進(jìn)行分析，并根據(jù)結(jié)構(gòu)及載荷的對(duì)稱(chēng)性，取結(jié)構(gòu)的一半作為分析對(duì)象。有限元分析模型的節(jié)點(diǎn)數(shù)為656，單元數(shù)為559。

在分析模型兩側(cè)的剖分面上，滿(mǎn)足剖分后的對(duì)稱(chēng)條件，沿著剖分表面自由滑動(dòng)，垂直剖分表面位移為0。

葉片與旋轉(zhuǎn)軸的連接齒面接觸部分，簡(jiǎn)化為垂直接觸面方向位移相同，可以傳遞壓力，沿著接觸面方向無(wú)摩擦自由滑動(dòng)條件。

葉片與旋轉(zhuǎn)軸的材料特性均為彈性模量21 000 kg/mm2，泊松比0.3。

由葉片上部的質(zhì)量和旋轉(zhuǎn)角速度(與交流電頻率相同)變換得來(lái)的離心力為416 104 kg。

由于葉片失效破壞的主要形式為葉片根部應(yīng)力集中導(dǎo)致的局部開(kāi)裂，所以這里將形狀優(yōu)化設(shè)計(jì)的目標(biāo)函數(shù)確定為葉片根部應(yīng)力集中的最小化。具體做法如下：對(duì)葉片根部和轉(zhuǎn)動(dòng)軸的4個(gè)連接齒處最大米賽斯應(yīng)力的和進(jìn)行最小化設(shè)計(jì)。得出如下關(guān)系式：

Min.σ=σA1+σA2+σA3+σA4+σB1+σB2+σB3+σB4

式中，σA1、σA2、σA3、σA4分別為葉片根部1、2、3、4號(hào)連接齒附近的最大米賽斯應(yīng)力；σB1、σB2、σB3、σB4分別為旋轉(zhuǎn)軸1、2、3、4號(hào)連接齒附近的最大米賽斯應(yīng)力。

由于對(duì)式(1)所示的目標(biāo)函數(shù)取極小值時(shí)，不能保證每一個(gè)連接齒處的應(yīng)力都滿(mǎn)足要求，所以，還需要增加優(yōu)化設(shè)計(jì)的約束條件，具體取為葉片根部和轉(zhuǎn)動(dòng)軸的4個(gè)連接齒處最大米賽斯應(yīng)力小于許用值：

σA1≤50 kg/mm2

σA2≤50 kg/mm2

σA3≤50 kg/mm2

σA4≤50 kg/mm2

σB1≤50 kg/mm2

σB2≤50 kg/mm2

σB3≤50 kg/mm2

σB4≤50 kg/mm2

考慮到加工和裝配等條件的限制，連接齒形狀不能任意地變化，各連接齒形之間必須始終滿(mǎn)足如下要求：

(1) 各連接齒尖始終位于同一條傾斜的直線上；

(2) 各連接齒尖之間的距離始終保持相等；

(3) 各連接齒尖的齒厚和傾斜角度始終保持一致。

綜合這些形狀變化的具體要求，得出優(yōu)化的基本形狀向量如下：

x1：各連接齒尖連線傾斜角度變化，-15°≤Δα≤15°；

x2：各連接齒尖連線厚度變化，-10 mm≤ΔL≤10 mm；

x3：葉片連接部分長(zhǎng)度變化，-10 mm≤ΔH≤10 mm；

x4：各連接齒尖傾斜角度變化，-5°≤Δβ≤5°；

x5：各連接齒尖角度變化，-3°≤Δγ≤3°；

x6：第一連接齒根部直邊傾斜角變化，-2°≤Δθ≤2°；

x7：第一連接齒根部曲率半徑變化，-2 mm≤Δr≤2 mm。

首先，將初始形狀的有限元分析網(wǎng)格的節(jié)點(diǎn)坐標(biāo)按照統(tǒng)一順序排成一個(gè)節(jié)點(diǎn)坐標(biāo)向量α0。

然后，每一個(gè)基本形狀生成相應(yīng)的有限元分析網(wǎng)格，并將其節(jié)點(diǎn)坐標(biāo)按照同樣的順序排成相應(yīng)的節(jié)點(diǎn)坐標(biāo)向量，即基本形狀向量α1、α2、α3、α4、α5、α6、α7。

接下來(lái)，將各坐標(biāo)向量代入下面的計(jì)算公式：

α=α0+x1(α1-α0)+x2(α2-α0)+x3(α3-α0)+x4(α4-α0)+x5(α5-α0)+x6(α6-α0)+x7(α7-α0)

其中，各坐標(biāo)向量均為固定不變的常值向量，右端可以計(jì)算得到一個(gè)與各坐標(biāo)向量長(zhǎng)度相同的新的坐標(biāo)向量，顯然易見(jiàn)，它對(duì)應(yīng)的是一個(gè)新的分析模型形狀。在這里，將各加權(quán)系數(shù)x1、x2、x3、x4、x5、x6、x7直接定義為形狀優(yōu)化設(shè)計(jì)的設(shè)計(jì)變量，通過(guò)調(diào)整設(shè)計(jì)變量的值可以達(dá)到調(diào)整優(yōu)化形狀的目的。

設(shè)計(jì)變量的變化范圍如下：-1≤xi≤1(i=1,2,…,7)。當(dāng)設(shè)計(jì)變量取-1時(shí)，表明該設(shè)計(jì)變量對(duì)應(yīng)的基本形狀沿負(fù)方向變化100%；當(dāng)設(shè)計(jì)變量取1時(shí)，表明該設(shè)計(jì)變量對(duì)應(yīng)的基本形狀沿正方向變化100%。

3優(yōu)化結(jié)果

全部?jī)?yōu)化計(jì)算經(jīng)過(guò)7次迭代得到最優(yōu)結(jié)果。優(yōu)化設(shè)計(jì)前后，設(shè)計(jì)變量的變化如表1所示。

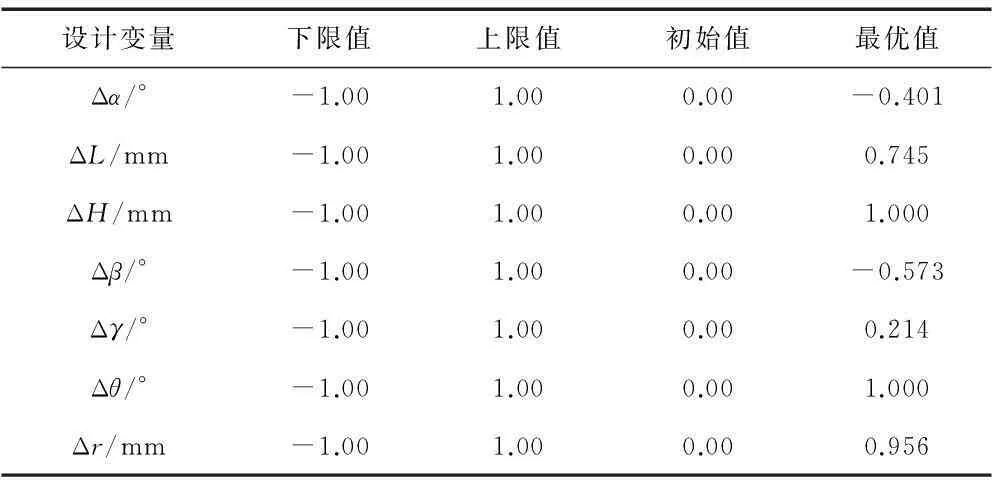
表1　優(yōu)化設(shè)計(jì)前后設(shè)計(jì)變量的變化

初始形狀與最優(yōu)形狀的對(duì)比以及優(yōu)化前后的應(yīng)力分布情況如圖2所示。

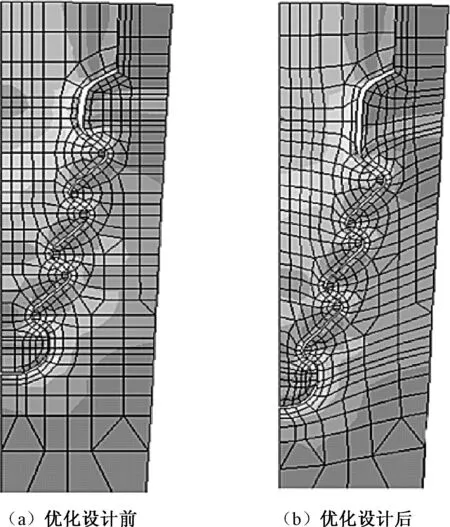
圖2　優(yōu)化設(shè)計(jì)前后的形狀變化和應(yīng)力分布比較

為了便于對(duì)優(yōu)化前后的應(yīng)力分布進(jìn)行分析和比較，將沿著葉片一側(cè)連接齒表面節(jié)點(diǎn)的米賽斯應(yīng)力以及旋轉(zhuǎn)軸一側(cè)連接齒表面節(jié)點(diǎn)的米賽斯應(yīng)力分別取出，整理曲線。

葉片一側(cè)連接齒表面節(jié)點(diǎn)的米賽斯應(yīng)力分布中，呈現(xiàn)上部第一齒應(yīng)力偏大、下部第四齒應(yīng)力偏小的趨勢(shì)。初始形狀的第一齒最大應(yīng)力遠(yuǎn)大于其他齒的最大應(yīng)力，即在第一齒附近發(fā)生較大的應(yīng)力集中現(xiàn)象；經(jīng)過(guò)優(yōu)化計(jì)算，優(yōu)化形狀的第一齒最大應(yīng)力已被調(diào)整回平均水平，各個(gè)齒的最大應(yīng)力明顯趨于均勻，達(dá)到了優(yōu)化設(shè)計(jì)的目的。

旋轉(zhuǎn)軸一側(cè)連接齒表面節(jié)點(diǎn)的米賽斯應(yīng)力分布中，呈現(xiàn)下部第四齒應(yīng)力偏大、上部第一齒應(yīng)力偏小的趨勢(shì)。初始形狀的第四齒最大應(yīng)力遠(yuǎn)大于其他齒的最大應(yīng)力，即在第四齒附近發(fā)生較大的應(yīng)力集中現(xiàn)象；經(jīng)過(guò)優(yōu)化計(jì)算，優(yōu)化形狀的第四齒最大應(yīng)力已被調(diào)整回平均水平，各個(gè)齒的最大應(yīng)力明顯趨于均勻。

由以上分析可知，優(yōu)化設(shè)計(jì)效果良好。由于葉片所受的離心力和葉片上表面面積不變，葉片所受的平均應(yīng)力不變，所以最佳優(yōu)化結(jié)果就是將葉片一側(cè)連接齒表面節(jié)點(diǎn)和旋轉(zhuǎn)軸一側(cè)連接齒表面節(jié)點(diǎn)所受應(yīng)力平均化，而上面的優(yōu)化結(jié)果正好達(dá)到此效果。

由表1可知，初始形狀的基本形狀向量的加權(quán)系數(shù)都為0，即各個(gè)基本形狀改變?cè)诔跏夹螤钪兴急壤秊?，而優(yōu)化形狀中，各個(gè)基本形狀發(fā)生了如下變化：各連接齒尖連線的傾斜角度Δα減小40.1%(-6.02°)，各連接齒尖連線的厚度ΔL增加74.5%(7.45 mm)，葉片連接部分長(zhǎng)度ΔH增加100%(10 mm)，各連接齒尖的傾斜角度Δβ減小57.3%(-2.87°)，各連接齒尖的厚度Δγ增加21.4%(0.64°)，第一連接齒根部直邊傾斜角Δθ增加100%(2°)，第一連接齒根部曲率半徑Δr增加95.6%(1.91 mm)。

4結(jié)論

經(jīng)過(guò)優(yōu)化設(shè)計(jì)，葉片根部的最大米賽斯應(yīng)力從初始形狀時(shí)的56.97 kg/mm2降低到優(yōu)化形狀的49.15 kg/mm2，應(yīng)力降低幅度為13.73%。

[參考文獻(xiàn)]

[1]孫靖民.機(jī)械優(yōu)化設(shè)計(jì)[M].北京：機(jī)械工業(yè)出版社，1999.

[2]隋允康，管昭，杜家政，等.位移、應(yīng)力、尺寸約束下二維連續(xù)體的形狀優(yōu)化[J].工程設(shè)計(jì)學(xué)報(bào)，2005(3).

[3]王世宏，趙希祿.基本形狀向量法在三維結(jié)構(gòu)優(yōu)化設(shè)計(jì)中的應(yīng)用[J].燕山大學(xué)學(xué)報(bào)，2000(2).

[4]王明強(qiáng)，朱永梅，劉文欣.有限元網(wǎng)格劃分方法應(yīng)用研究[J].機(jī)械設(shè)計(jì)與制造，2004(1).