基于FPGA的通用型FIR數字濾波器的研究與設計

摘要：FIR數字濾波器的實現是基于加法器和乘法器，通過延遲將輸入信號與固定的抽頭系數相乘累加得到濾波結果，其中濾波系數是已知的數值，當我們需要一個固定階數系數的值不固定時，我們就需要將濾波的系數通過外部輸入的方式再與輸入信號相乘。對于FIR數字濾波器的通用型的研究是基于傳統的串行FIR數字濾波器的結構進行改造，使用VerilogHDL語言在QuartusII和Modelsim軟件里面進行設計和仿真。結果表明基于FPGA的通用FIR數字濾波器的設計是可行的。

關鍵詞：加法器；乘法器；串行FIR數字濾波器；串行結構；通用型FIR數字濾波器

中圖分類號：TN713+.7

文獻標識碼：A

DOI：10.3969/j.issn.1003-6970.2015.06.023

本文著錄格式：張震，基于FPGA的通用型FIR數字濾波器的研究與設計叮].軟件，2015，36（6）：125-128

ResearchandDesignofUniversalFIRDigitalFilterBasedonFPGA

ZHANGZhen

[Abstract]：FIRdigitalfilterisrealizedbasedonaddersandmultipliers.Bydelayingthemultiplicationaccumulationoftheinputtedsignalandthefixedtapcoefficients，thefilterresultsareobtained.Thefiltercoefficientisknown.Whenafixedordernumbercoefficientvalueisnotfixed，weneedtomultiplythefiltercoefficientsthroughexternalinpulwiththeinputsignal.ResearchonuniversaltypeofFIRdigitalfilterisbasedontraditionalserialFIRdigitalfilterstructuretransformation，usingVerilogHDLlanguageinquartusandModelsimsoftwarefordesignandsimulation.TheresultsshowthatthedesignofgeneralFIRdigitalfilterbasedonFPGAisfeasible.

[Keywordsl：Adder；Multiplier；FIRdigitalfilter；Serialstructure；GeneralFIRdigitalfilter

0引言

研究人員自20世紀中期以來不斷的研究與發現，并且提出了一整套關于數字濾波器的相關理論。數字濾波器[1-3]是對輸入的數字信號進行相應的累乘加運算得到輸出的濾波信號的處理。利用FIR數字濾波器可以將不同的信號進行處理，從而提取出我們需要的信號而過濾掉干擾信號。不同的實現方法可以分為FIR數字濾波器和IIR數字濾波器[4]。由于FIR數字濾波器是可以實現線性相位的，并且它的單位沖擊響應為有限長，因此FIR數字濾波器的系統是總是穩定的[5]。對于數字濾波器具有很強的穩定性、高精度性、靈活性等等比較優秀的特點，隨著數字濾波技術的不斷發展，FIR數字濾波器在信號處理、數字圖像處理以及通信領域等等應用也是十分的廣泛[6]。

FIR數字濾波器的系數的實現有兩種方式，一種方式是可編程型的，另一種則是固定型的.對于可編程的系數實現使用起來比較的靈活，固定型的有利于實現高速度和低功耗的系統實現，本文使用的是可編程的。

對于階數為N的FIR數字濾波器的實現，它的表達式為：

在實現FIR數字濾波器的方法中，使用FPGA的硬件實現可以使得FIR數字濾波器具有速度快的優點。但是對于階數越多實現的FIR數字濾波器消耗的硬件資源也是比較多的，因此本文實現的通用型FIR數字濾波器是以低階的方式來實現和驗證的。

1FIR數字濾波器的基本原理

1.1濾波器的一般表示方式

對于FIR數字濾波器的數學表達式也可以表示成[7]：

式（1）中：N-濾波器的階數；h（n）-第n級的抽頭系數（單位脈沖響應）；x（n）-第n時刻的輸入信號。FIR數字濾波器的h（n）單位脈沖響應是有限長的，也就是FIR數字濾波器是一個有限長的序列與輸入信號的乘積累加和實現的，從式（1）中可以看出FIR數字濾波器是由一個加法器和乘法器的集合構成的，對于每一次的采樣都要進行N次的乘法和（N-l）次的加法運算。其中的單位脈沖響應h（n）為實數，在幅度上滿足對稱條件

h（n）=土h（N_n）。

1.2串行FIR數字濾波器的結構設計

對于h（n）做z域變換可以得到FIR數字濾波器的系統函數H（z），其系統函數表達式為：

n=U

由此可以得到FIR數字濾波器的串行結構示意圖如下圖1所示：

圖1中x（n）為輸入的待處理信號；h（n）為固定的系數，其脈沖響應的數值是已知確定的數值；z-l代表著輸入信號的延遲。但是在通用型FIR數字濾波器的實現當中h（n）單位脈沖響應是通過相同的時鐘周期逐個地輸入再與相應的輸入延遲信號相乘的，輸入的單位脈沖是可以根據白己的實際需要來變化的輸入的，因此達到了通用型FIR數字濾波器的實現。

1.3加法器

加法器[8-9]是數字信號處理過程中最常用、最簡單的邏輯單元。在很多的運算過程中都需要用到加法器，減法和乘法的過程轉換也可以通過加法器來實現。在FIR數字濾波器的實現當中我們需要通過加法器對乘法器運算的結果進行累加得m濾波器的輸出結果。對于加法器也有不同的結構實現，不同的加法器的實現方式的不同使得對資源、速度的結果也是不一樣的。下面讓我們簡單的了解加法器的實現原理。

加法器有半加器和全加器，半加器是沒有地位進位端的加法器，而全加器相比于半加器多了一個進位輸入端，全加器的真值表見表1。

通過上表1的全加器真值表我們就可以得l斗J全加器的邏輯表達式為：

S=AABACin：

C_out=（A&B）|（（AAB）&C_in）；

從全加器的表達式可以看出和的值與輸入信號和進位信號異或的到，進位信號同樣與輸入信號和進位信號相關。

1.4乘法器

乘法器[10]同樣是信號處理的基本邏輯單元之一，比較常用的像濾波器、FFT都需要使用到乘法器。乘法器的實現也是有多種的，下面我們介紹在數字信號處理當中比較常用的一位相加乘法器。

移位相加乘法器的實現相對簡單，就是對數進行二進制的轉化進行相乘來實現。一位乘法器是根據乘數的每一位是0或1來判斷被乘數是否移位相加，如果為1則被乘數移位相加，否則被乘數不想加。

一位乘法器的實現過程如下：

例如一個3bit乘法器需要一個6bit移位寄存器和一個6bit的加法器就可以實現。

2通用型FIR數字濾波器的研究與設計

2.1通用型FIR數字濾波器的原理

通用型的FIR數字濾波器與FIR數字濾波器的設計基本上相同。通用型的原理就是在FIR數字濾波器的基礎之上對FIR數字濾波器的單位脈沖響應做一些處理，具體的處理就是將h（n）的單位脈沖響應的數值通過外部可輸入的方式，經過寄存器寄存，寄存器的時鐘周期和輸入信號的時鐘為同一個時鐘，每一個時鐘輸入信號延遲一位的同時單位脈沖響應也進行延遲，最后與相應的延遲輸入信號進行相乘在相加，輸出的結果就是濾波輸出。

2.2通用型FIR數字濾波器的結構設計

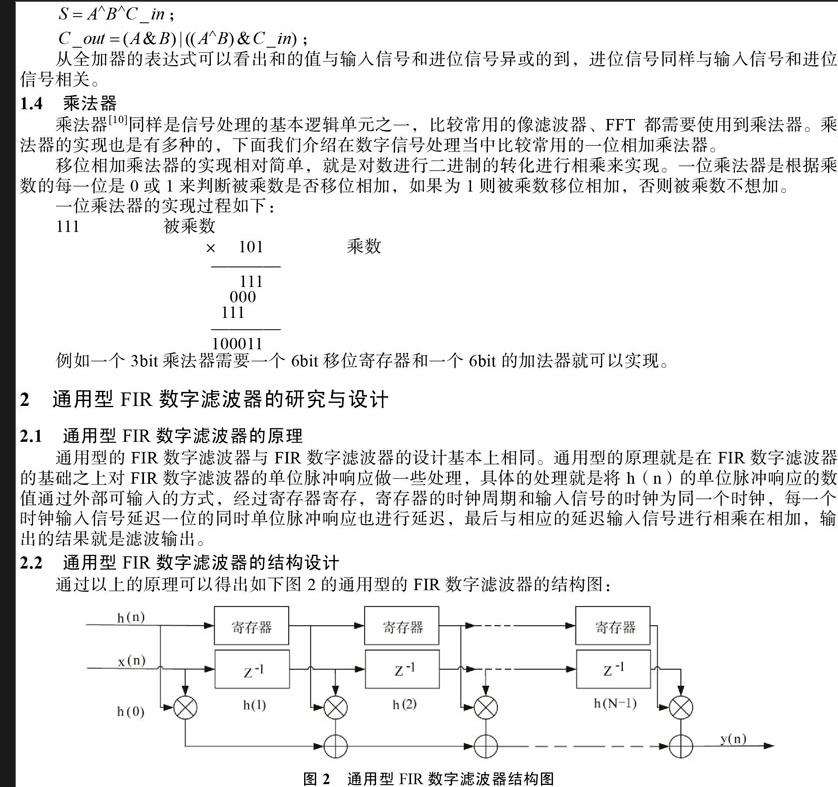
通過以上的原理可以得出如下圖2的通用型的FIR數字濾波器的結構圖：

從圖2和圖1的對比我們可以發現通用型FIR數字濾波器與一般的FIR數字濾波器的不同。一般的FIR數字濾波器的脈沖響系數應是固定的和每一個延遲信號直接相乘，而對于通用型的FIR數字濾波器的脈沖響應系數是通過引出輸入端口進行輸入的脈沖，這個輸入的脈沖是根據自己的需要來編寫脈沖響應系數的數值的，從而達到了通用型的目的。

對于通用型的FIR數字濾波器的表達式其輸出的方式其實和式（1）-樣的，只是通用型的結構上和輸入方式上的不同，通用型是脈沖響應系數的值通過設置一個輸入的端口，通過這個端口來輸入脈沖響應系數的值得方式，而這個值是可以改變的。

3通用型FIR數字濾波器的設計驗證

3.1設計實現

下面通過VerilogHDL語言通過QuartusII和Modelsim軟件來設計一個8階通用的FIR數字濾波器設計并進行驗證。FIR數字濾波器的數據相系數為有符號的9位數，FIR數字濾波器的階數是L=8，因此在設計中加法器的位數為：9+9+log2（/）一1=20。處理的第一步就是先set，如果setx=0就將濾波器的脈沖響應系數輸入到抽頭延遲線上，否則就將數據下載到x寄存器中；第二步執行乘積和的計算，對乘積進行一位有符號擴展，并加到前面的部分乘積和上。所有的乘法器為3級流水線結構。最后輸出y_out除以256后輸I斗『。

3.2驗證

3.2.1代碼實現

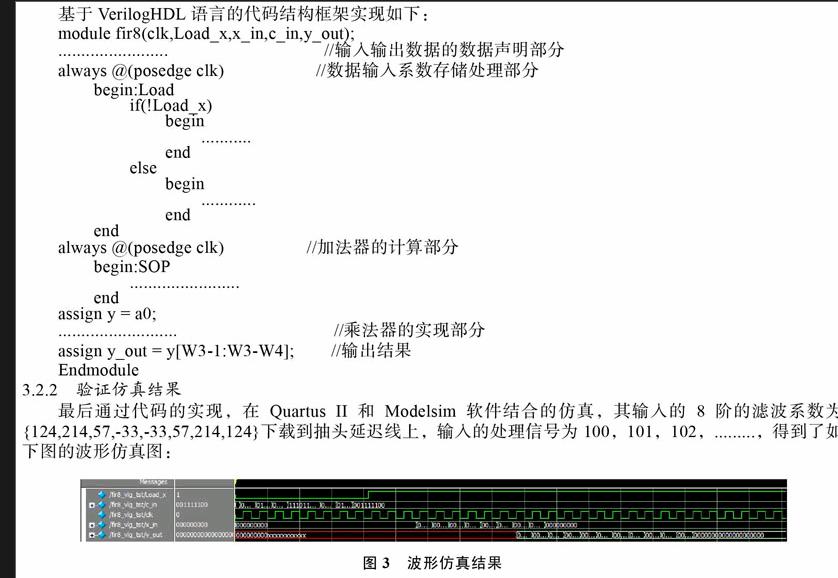
基于VerilogHDL語言的代碼結構框架實現如下：

3.2.2驗證仿真結果

最后通過代碼的實現，在QuartusII和Modelsim軟件結合的仿真，其輸入的8階的濾波系數為{124，214，57，-33，-33，57，214，124}下載到抽頭延遲線上，輸入的處理信號為100，101，102，…….，得到了如下圖的波形仿真圖：

4結語

本文主要介紹了基于FPGA的串行濾波器的一般實現結構進行一些改進來實現通用型FIR數字濾波器的設計，根據串行結構實現的FIR數字濾波器的原理和結構，將串行結構的FIR數字濾波器的脈沖響應系數通過同一個時鐘（clk）下載到濾波器當中，然后再與輸入的信號進行累乘加的運算得到通用型的FIR數字濾波器。同時闡述了通用型這種設計方法的思想和原理實現方法，根據實驗結果證明了通用型FIR數字濾波器的實現的可行性。通過這個實現的方法找到了另外一種實現FIR數字濾波器的實現方式，由于具有通用性對于硬件的資源可以重復的利用，具有很強的研究意義。

參考文獻

[1]高學金，齊詠生，王普，基于卡爾曼濾波器和多向核主元分析的發酵過程在線監測[J].新型工業化，2011，1（9）：102-110.

[2]劉雪艷，張雪英，黃麗霞.Gammachir濾波器組在語音特征提取中的應用[J].新型工業化，2011，1（11）：21-28.

[3]祖霄鵬，肖建康，朱文軍.新型正六邊形微帶多模帶通濾波器[J].新型工業化，2011，1（12）：113-116.

[4]胡廣書.數字信號處理理論、算法與實現[M].北京：清華大學出版社，2003.

[5]吳鎮揚.數字信號處理[M].北京：高等教育出版社，2004.

[6]李金明.數字FIR濾波器在監控系統中圖像信號處理方面的應用[D].蘭州：蘭州理T大學，2006.

[7]王正彥，范延濱.用FPGA實現FIR濾波器算法研究[J]測控技術，2004，23（zl）：123-126.

[8]朱小佩，蕭蘊詩，岳繼光.基于流水線結構的8位超前進位加法器設計[J].電子工程師，2009，9（31）：1.

[9]王悅，陳濤.基于FPGA的流水線珠算加法器設計[J].科學技術與工程，2013，11（32）：1.

[10]鞠芳，馬昕，田嵐.基于FPGA的數字乘法器性能比較[J].電子器件，2011，06：1.