IDIRECT-HDMR高維近似模型方法及工程應用

黃志遠，邱浩波，蔡習文

(華中科技大學 機械科學與工程學院，湖北 武漢 430074)

?

IDIRECT-HDMR高維近似模型方法及工程應用

黃志遠，邱浩波，蔡習文

(華中科技大學 機械科學與工程學院，湖北 武漢 430074)

摘要：元建模常用于近似求解輸入與輸出間的映射關系。隨著維度的增加，其計算成本將呈指數增長，使得常用的回歸方法難以獲得高精度的近似模型。提出一種基于改進分割矩形IDIRECT(improved dividing rectangles)采樣的高維模型表示HDMR(high-dimensional model representation)方法，稱為IDIRECT-HDMR。該方法將高維問題轉化為一系列低維問題求和，從而用較少的樣本點獲得較高精度的近似模型。采用多維度的數值算例驗證IDIRECT-HDMR的可行性并將其應用于工程實例。

關鍵詞：元建模；分割矩形；高維模型

0引言

近年來，元建模技術廣泛運用于工程優化的近似求解問題。常用的近似建模方法有：多項式回歸PR(polynomial regression)[1]、克里金插值(Kriging)[2]、徑向基函數RBF(radial basis function)[3]、最小移動二乘法MLS(moving least square)[4]等。這些方法在提高建模效率以及模型精度上有了一定的發展，但實踐證明僅適用于低維問題，對于高維問題，要保證模型精度，其計算成本將隨維度的增加呈指數增長。

文中提出了一種基于IDIRECT采樣的高維模型表示方法，IDIRECT-HDMR。這種方法結合了HDMR的層次結構優勢以及IDIRECT的智能采樣策略，從而利用少量的樣本點構建出高精度的近似模型。

1基本理論

1.1HDMR

(1)

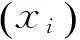
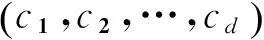
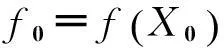
(2)

(3)

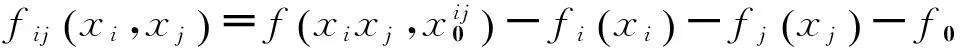
(4)

…

(5)

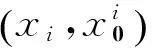
當式(1)中的所有組成函數構建完成，則用這個HDMR表達式取代原物理模型。式中每一項都有鮮明的數學含義，如果輸入變量間沒有任何相關關系，那么表達式中只含零階項和一階項。實驗證明，高階項對輸出函數的影響是有限的，在大多數工程問題中，這種影響可以忽略不計，HDMR展開到二階項時就足夠反映出原物理模型。

1.2IDIRECT采樣方法

DIRECT[9]算法主要用于求解帶邊界約束的最優問題，它能權衡全局與局部的尋優關系，且收斂速度快、魯棒性強。當最優點確定后，就可以在它附近區域構建HDMR近似模型，這將有效地縮減原設計空間。不失一般性，DIRECT通常將設計空間歸一化為單位超立方：

(6)

c1表示這個超立方中心。對點ci±δei,i=1,2,…,d進行采樣，其中δ等于立方體邊長的1/3，ei是第i個歐幾里德向量。得到對應點的評價函數值并取最優值wi：

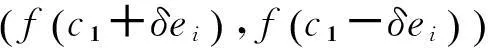
(7)

然后將wi所在的區域劃分為三等份，ci±δei則成為新的超矩形中心，重復這個過程直到滿足收斂準則。

雖然DIRECT采樣方法能有效地縮減樣本空間，但將其引入函數逼近問題時，會產生一個難以避免的誤差，即求得的近似模型在邊界區域的逼近能力較差。為了獲得精度更高的回歸模型，本文改進了DIRECT的采樣策略。

由于DIRECT采樣過程不選擇邊界點，而邊界區域的樣本點通常又影響著建模精度，因此，主要的改進策略為：當原方法對超立方中心采樣取值后，不直接對點ci±δei,i=1,2,…,d進行采樣，而是先對各維度的邊界點采樣取值，然后再通過評價函數進行后續的劃分采樣。圖1表示了一個二維問題，采用IDIRECT的劃分策略。圖中每一行代表一個新的迭代過程，第一列到第二列的轉變表示潛在最優超矩形的識別。第二列的陰影區域表示對潛在最優超矩形的選擇。第三列指潛在最優超矩形劃分結束的狀態。

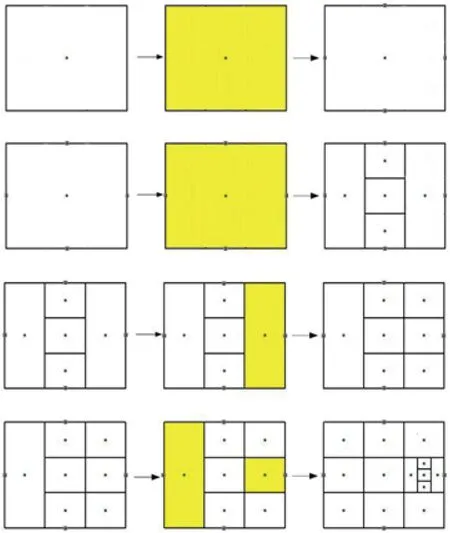
圖1　IDIRECT的劃分策略

1.3IDIRECT-HDMR近似模型方法

在對原模型函數逼近時，底層函數的特性通常是未知的，尤其是黑箱求解問題。IDIRECT-HDMR可以通過較少的樣本點獲得原模型輸入與輸出間的映射關系。其具體求解步驟為：

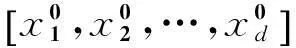
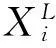
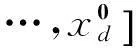
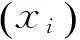
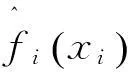
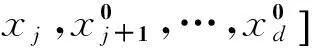
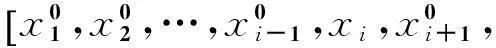
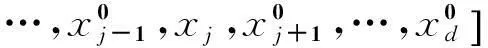
影響建模的計算成本主要有三個因素：維度、變量的取值范圍以及收斂準則。當其他條件不變，僅考慮維度變化時，IDIRECT-HDMR展開到l階的計算成本為：

(8)

式中，s是每個維度的采樣個數。計算成本隨著維度d的增加呈多項式增加。而常用的近似方法采用全因子設計時，其計算成本達到sd。因此，IDIRECT-HDMR大大降低了建模成本，若其表達式僅展開到二階項時，建模效率將進一步得到提高。

2算例分析2.1評價指標

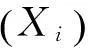
(9)

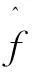
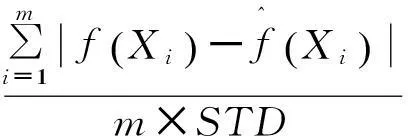
(10)

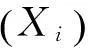
RMAE=

(11)

這是評價近似模型局部精度的重要指標，它描述了設計空間某一局部區域的誤差，且RMAE越小越好。

2.2函數算例

如表1所示，使用4個典型的測試算例，其中包括兩個低維函數(二維與三維)和兩個高維函數(十維)。采用IDIRECT-HDMR構建它們的近似模型，通過3個評價指標驗證模型的函數逼近能力。取測試樣本點個數為1000，測試結果如表2所示，NOP表示構建模型所需的樣本點數。

表1　測試函數

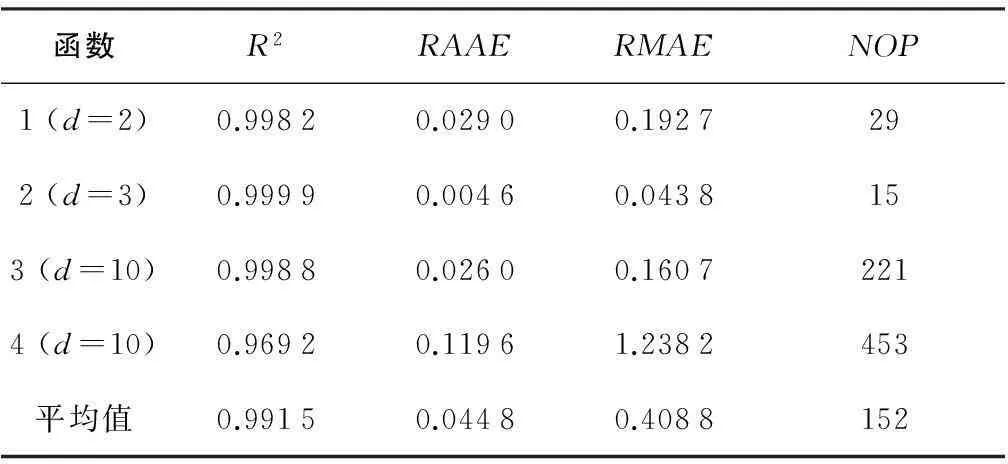
表2　測試函數評價結果

表2數據可知，無論高維還是低維的測試函數，IDIRECT-HDMR構造的近似模型都有很高的函數逼近能力，且所需的樣本點也較少。針對以上算例，學者Simpson[10]采用傳統的近似方法進行了回歸驗證，圖2給出了各評價指標的平均值，3個評價指標均明顯比本文提出的近似方法所得的結果差。因此， IDIRECT-HDMR相對其他近似方法而言，能更精確地求解高維模型的函數逼近問題。

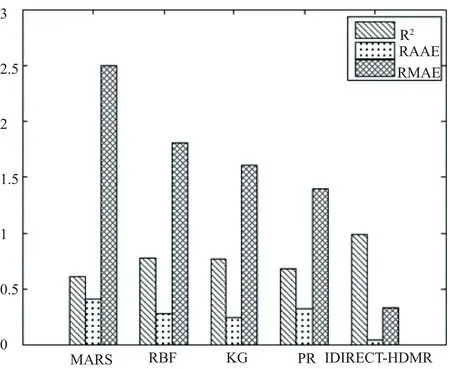
圖2　各種近似模型評價指標的柱狀圖

2.3工程算例

圖3是一個立柱的三維模型，立柱左側有一引導橫梁上下移動的導軌。機床加工過程會使導軌發生撓度變形，導致橫梁不能沿垂直方向運行，影響機床的加工精度。因此，在對機床進行結構設計前，必須找到立柱各尺寸參數與導軌撓度變形間的映射關系。選用立柱的8個尺寸參數作為設計變量，導軌的撓度變形為響應。

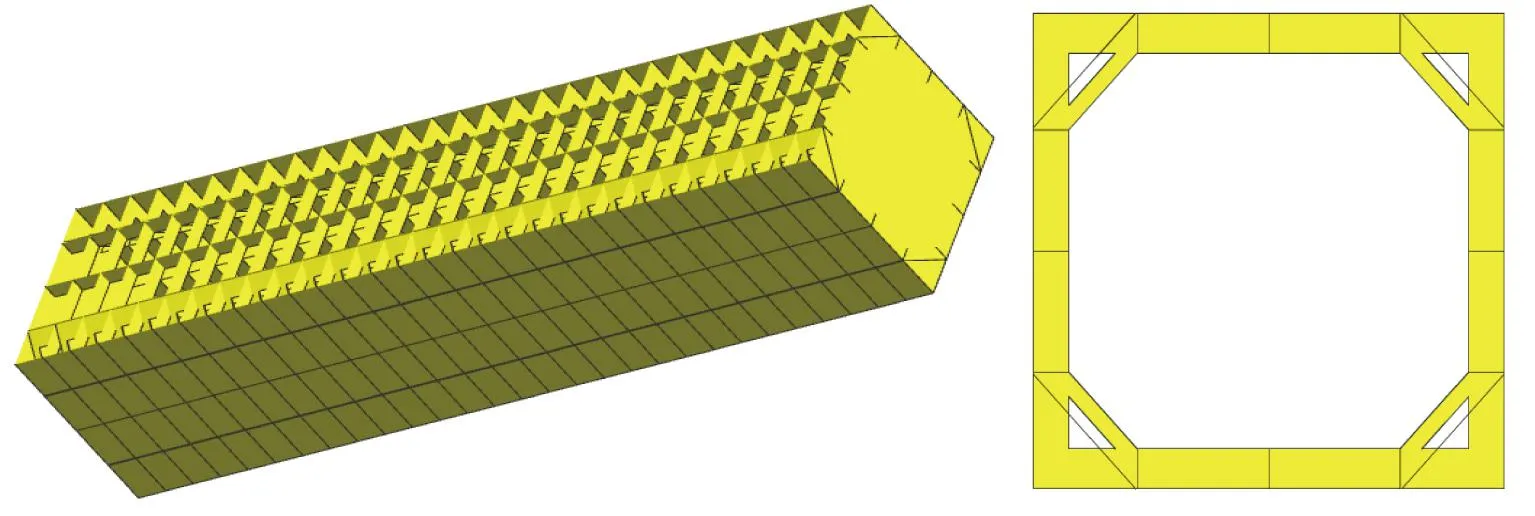
圖3　立柱的三維模型

利用Hypermesh網格化分，獲得其有限元模型。并采用OptiStruct求解器對該模型進行有限元分析。由于立柱每一次尺寸參數的變化都需要重新建模求解，導致每獲取一個樣本點都要耗費大量的時間，應利用盡可能少的樣本點獲得較高精度的近似模型，因此采用IDIRECT-HDMR近似建模方法。并隨機生成了一組測試樣本點驗證模型的近似精度，結果如表3所示。

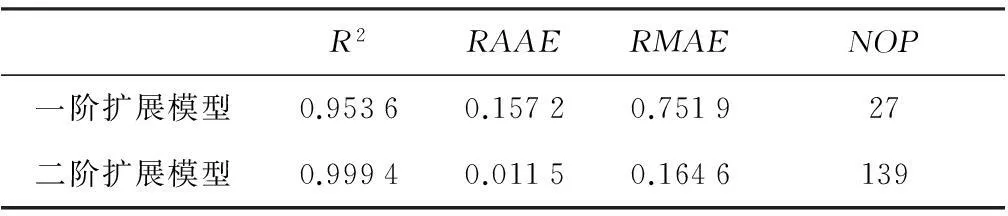
表3　工程算例測試結果

表3中，一階擴展模型表示IDIRECT-HDMR近似模型僅擴展到一階項，即模型只含常數項和一階項；二階擴展模型表示近似模型擴展到了二階項。根據表中結果可知，采用文中提出的IDIRECT-HDMR方法能夠用少量的樣本點構造出高精度的近似模型。因此，在求解此高維工程問題時，IDIRECT-HDMR有著極高的求解效率和近似精度，并且模型的構建過程可以得到各變量間的耦合關系，這有助于立柱的結構設計。比較一階擴展模型和二階擴展模型可知，一階擴展模型也有相對較高的精度，且模型的構建只需極少的樣本點。因此，在一些對精度要求不高，但需快速獲取近似模型的工程應用中，有時可以將IDIRECT-HDMR模型只擴展到一階項。

4結語

提出的IDIRECT-HDMR近似模型方法獲得了較高的精度和建模效率，并成功運用于工程實例中。該方法的主要優勢總結為以下幾點：

1) 采用HDMR結構，將高維問題轉化為一系列低維問題求和。隨著維度的增加，計算成本從指數增長降為多項式增長。

2) 采用IDIRECT采樣方法，提高了模型的收斂速度并控制了采樣數量。

3) 該方法能夠自主地判斷函數的線性與否以及各變量間的相關關系。

4) 相對其他的近似方法，IDIRECT-HDMR能更好地保證模型精度與建模效率。

雖然IDIRECT-HDMR近似模型方法在一定程度上解決了高維建模的困難，并獲得了一定的應用前景。但是本方法還有較大的發展空間，例如采樣方法的深入研究；模型擴展階數的合理選擇等。對于一些復雜工程算例，如含有噪聲的工程系統，該方法需要進一步地完善和發展。

參考文獻:

[1] Caglar, H. and N. Caglar, Solution of fifth order boundary value problems by using local polynomial regression. Applied mathematics and computation, 2007，186(2): 952-956.

[2] ZENG, H.-e. and S.-x. HUANG, Research on spatial data interpolation based on Kriging interpolation [J]. Engineering of surveying and Mapping, 2007，5: 001.

[3] Guillén, A., et al., Output value-based initialization for radial basis function neural networks. Neural Processing Letters, 2007，25(3): 209-225.

[4] Breitkopf, P., et al., Moving least squares response surface approximation: formulation and metal forming applications. Computers & structures, 2005，83(17): 1411-1428.

[5] Rabitz, H. and ?.F. Ali, General foundations of high‐dimensional model representations. Journal of Mathematical Chemistry, 1999，25(2-3): 197-233.

[6] Wang, H., L. Tang, and G. Li, Adaptive MLS-HDMR metamodeling techniques for high dimensional problems. Expert Systems with Applications, 2011，38(11): 14117-14126.

[7] Shan, S. and G.G. Wang. Development of adaptive RBF-HDMR model for approximating high dimensional problems. 2009，ASME.

[8] Li, G., et al., High dimensional model representations generated from low dimensional data samples. I. mp-Cut-HDMR. Journal of Mathematical Chemistry, 2001，30(1): 1-30.

[9] Finkel, D.E., DIRECT optimization algorithm user guide. Center for Research in Scientific Computation, North Carolina State University, 2003， 2.

[10] Simpson, T.W., Comparative studies of metamodeling techniques under multiple modeling criteria. 2000.

歡迎投稿歡迎刊登廣告歡迎訂閱

IDIRECT-HDMR Approximation Model for High Dimensional

Problems and Engineering Application

HUANG Zhi-yuan, QIU Hao-bo, CAI Xi-wen

(School of Mechanical Science and Engineering; Huazhong University of Science & Technology, Wuhan 430074, China)

Abstract:Metamodeling is often used for approximate mapping between the input and output variables. Popular regression methodologies are inapplicable to the accurate metamodels for high dimensional practical problems since the computational time increases exponentially as the number of dimensions rises. This paper proposes a new form of high-dimensional model representation (HDMR) by integrating an intelligent sampling strategy, namely, Improved Dividing Rectangles (IDIRECT), termed IDIRECT-HDMR. In this method, few sample points are used to obtain accurate metamodels by transforming a high dimensional problem into a series of low dimensional problems. Some mathematical test functions with a wide scope of dimensionalities are used to demonstrate the performance of IDIRECT-HDMR, and this method is applied to the practical application example.

Keywords:metamodeling; dividing rectangles; high-dimensional model

基金項目：福建省自然科學基金資助項目(2013J01185)；福州大學人才基金資助項目(XRC-1157)

收稿日期：2014-12-03

中圖分類號：TP391.9

文獻標志碼：B

文章編號：1671-5276(2015)03-0100-04

作者簡介：黃志遠(1989-)，男，江西南昌人，碩士研究生，主要研究方向為高維模型近似求解策略與結構優化設計。