雙視線角比例-微分主動防御導引律設計

王哲，王小平，劉哲，狄方旭，程建鋒

(1.空軍工程大學 航空航天工程學院，陜西 西安710038;2.空軍西安飛行學院 理論訓練系，陜西 西安710300)

0 引言

現代空戰中，機載導彈的攻防對抗日趨激烈，采用各種先進技術的空空導彈層出不窮，來襲導彈的攻擊已成為作戰飛機的最大威脅。作戰飛機只有有效保存自己，才能達到空中作戰的基本目的［1］。空戰過程中，如何實現目標機對來襲導彈的成功逃逸是目前一個亟待解決的難點問題。目標機的成功逃逸不僅能極大提高飛機及飛行員的生存率，而且會極大提高我方的空中作戰優勢。

針對這類問題，國內外很多專家學者進行了深入的研究，提出了很多解決辦法。但是目前大多數的研究僅考慮了如何通過飛機自身機動或拋射紅外誘餌去規避來襲導彈，即被動的飛機防御手段。文獻［2］提出了一種基于導彈導引律辨識的飛機逃逸軌跡優化方法，并對飛機末端機動逃逸策略進行了研究。文獻［3］對飛機逃逸導彈策略進行了分析，提出了基于Gauss偽譜法-遺傳算法的機動規避導彈策略和紅外誘餌干擾下規避導彈效能定量評估及機動逃逸策略。文獻［4］研究了飛機在被導彈迎面攻擊時的最佳逃逸策略，提出并分析對比了幾種突防方案，即機動變軌技術、拋射誘餌以及綜合這兩種突防方案。此外，Shima等學者提出了通過飛機發射防御導彈去攔截來襲導彈的方法［5-8］，即“主動防御技術”。主動防御技術克服了一般逃逸策略會使目標機一直處于被動態勢的缺點，化被動為主動。它在對來襲導彈實施攔截的同時，能主動搶占有利態勢發射攻擊導彈，對敵機實施攻擊。

本文提出了一種三視線重合的主動防御策略，并在此基礎上設計了一種基于雙視線角的比例-微分主動防御導引律。

1 問題的提出

1.1 主動防御的概念

一般而言，作戰飛機通常采用反探測、反跟蹤和反攻擊等被動防范措施，如飛機結構外形隱身、施放無源誘餌和強功率有源干擾等，以規避和誘騙對方的空空導彈。隨著進攻性空空導彈技術的不斷完善，這種消極被動的逃避方式幾乎不能確保飛機的有效生存［9］。此外，空戰過程中，一旦敵方發射導彈，即使之前我方處于非常有利的攻擊態勢，基于被動防御技術，我方也會馬上進入防守態勢從而喪失優勢。主動防御技術的出現克服了這個缺點，能很好地保持被攻擊之前的優勢。

主動防御是指在作戰飛機遭遇來襲導彈攻擊時，主動發射防御導彈對來襲導彈進行攔截，來實現對作戰飛機的保護。主動防御具有很實際的飛機保護和很強的心理保護作用，能夠保證作戰飛機不用改變原有的作戰任務和攻擊態勢，并在防守的同時展開攻擊，極大地控制了戰場的主動權和作戰時機，能在防守反擊中更快地尋求制勝的機會。另外，主動防御技術不但適用于作戰飛機，而且適用于預警機等大飛機以及艦艇的防御。

1.2 主動防御策略

為了方便研究，本文進行如下假設:

(1)為了便于研究，文中目標機、攻擊導彈、防御導彈可簡化為T(Target)，M(Missile)，D(Defender);

(2)目標機、攻擊導彈、防御導彈在同一平面內運動;

(3)交火過程中，目標機和導彈不會發生故障;

(4)交火過程中的各種信息是完全可獲得的;

(5)將目標機、攻擊導彈、防御導彈都視為質點。

目標機-攻擊導彈-防御導彈的相對運動關系如圖1所示。圖中:φT，φM，φD分別為目標機、攻擊導彈和防御導彈組成的三角形的內角;σ為D的外角;LOSij為 i，j(i，j=T，M，D)兩者之間的視線;η 為防御導彈到視線LOSTM的距離。

圖1 目標機-攻擊導彈-防御導彈的相對運動關系Fig.1 Target-Missile-Defender engagement

對于目前最常用的比例(PN)導引律來說，當追蹤目標為靜止或速度、機動性遠弱于攻擊導彈時攔截效果良好。然而，當目標機動性提高時，攻擊導彈所付出的代價將會是原來的倍。另外，在主動防御問題中，來襲導彈在速度以及機動性上并不屬于防御導彈，因此PN導引律若作為防御導彈導引律效果將差強人意［10-11］。

為了實現防御導彈對來襲導彈的攔截，本文設計了三視線重合(三點共線)的主動防御策略，即控制防御導彈始終位于目標機T與來襲導彈M之間，如圖2所示。此時，目標機、防御導彈和來襲導彈垂直于視線方向的速度分量相同，三者沿視線方向運動，這樣就保證了來襲導彈在捕獲目標機之前被防御導彈所攔截，達到飛機主動防御的目的。

圖2 主動防御策略Fig.2 Active defense strategy

實現主動防御技術，從數學上來講有以下幾種方法:φT→0;φM→0;φM→π 或 σ→0;η→0。盡管誤差距離η可以作為主動防御實現的被控量，但是實際中η并不能直接進行測量。因此，本文以角度作為被控量設計主動防御導引律，以完成主動防御策略。

2 主動防御導引律設計

目標機-攻擊導彈-防御導彈的運動模型如圖3所示。圖中:(λtd，λdm，λtm)分別表示視線(LOSTD，LOSMD，LOSTM)的視線角;ac為防御導彈D的指令加速度，ac垂直于VD;ac⊥LOS為ac垂直于TM的分量;χ為 ac⊥LOS與 ac的夾角。令 α1=φT，α2=φM，α3=σ。

圖3 目標機-攻擊導彈-防御導彈運動模型Fig.3 Target-Missile-Defender motion model

由圖3可知:α1=λtm-λtd;α2=λdm-λtm;α3=λdm-λtd。由 ac與 ac⊥LOS的幾何關系可知:

考慮到1/cosχ的值域，為了防止控制指令加速度(側向過載)發散，引入變量λ，并令λ為:

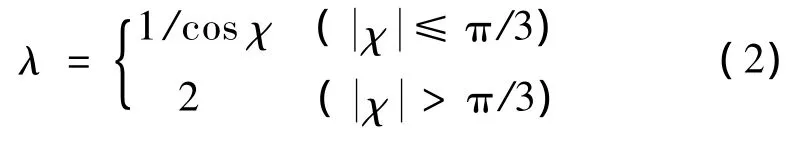
此時式(1)變為:

基于角度的主動防御導引律的目的是控制αi→0，i=1，2，3。分別以角度 αi作為被控量，構造比例控制如下:

式中:N為導航常數;VC為防御導彈D與來襲導彈M的閉合速度(接近速度)。

考慮到比例控制的作用僅是放大誤差的幅值，因此僅比例控制不足以完成主動防御的任務。然而，通過增加微分項，可以對角度誤差變化的趨勢進行預測，能夠提前使抑制誤差的控制作用等于零，改善系統在控制過程中的動態性能。給ac⊥LOS增加一個角速度分量為角速度導航常數)，即微分項，這時 ac⊥LOS變為:

此時ac⊥LOS就變成一個比例微分控制。且對于式(5)，若 Nd=0，則式(5)等于式(4)。代入式(3)可得主動防御導引律為:

仿真中，給定初始時刻目標機、來襲導彈、防御導彈的速度分別為 250 m/s，800 m/s，800 m/s(忽略防御導彈的加速時間)，來襲導彈與目標機相距20 km，且與目標機的夾角60°，最大過載50，來襲導彈使用PN導引律。

防御導彈導引律無微分項(Nd=0)情況下，其主動防御導引律的攔截時間及脫靶量如表1所示。由表1可以看出，僅采用比例控制時無法完成主動防御任務，即驗證了上文的假設。防御導彈導引律帶微分項(Nd=3)情況下，其主動防御導引律的攔截時間及脫靶量如表2所示。表2給出的數據顯示，采用α1時防御導彈的脫靶量不符合標準。

表1 Nd=0時攔截時間及脫靶量Table 1 Simulation results with Nd=0

表2 Nd=3時攔截時間及脫靶量Table 2 Simulation results with Nd=3

圖4和圖5為Nd=3時不同角度下的指令加速度及誤差距離。

圖4 Nd=3時的指令加速度Fig.4 Acceleration commands with Nd=3

圖5 Nd=3時的誤差距離Fig.5 Distance errors with Nd=3

由圖4給出的指令加速度可以看出，采用角α1和α3時，指令加速度開始較大，很快收斂至0，而采用α2指令加速度則有明顯的振蕩。圖5給出的誤差距離表明，采用α3時系統的誤差距離幅值變化最小。

綜上所述，可以得到采用α3作為被控量的主動防御導引律效果最好的結論。因此，本文選用外角σ(α3)作為被控量的主動防御導引律，其表達式如下:

觀察圖4可以看出，α1曲線和α3曲線在初始階段存在明顯的振蕩，分析其原因主要是因為角α1和α3都含有λtd項，而角 α2不含，在防御導彈發射之后的初始階段，目標機T與防御導彈D相距較近，λtd比較活躍，造成指令加速度在初始階段的振蕩。

為了驗證λtd對指令加速度的影響，假設在上述仿真的基礎上，給來襲導彈與防御導彈同樣的軸向加速度，其余保持不變，進行仿真驗證，仿真結果如圖6所示。其中給定軸向加速度aaxial為:

圖6 具有軸向加速度下的仿真結果Fig.6 Simulation results under axial acceleration

此時，防御導彈的脫靶量為4.905 3 m，說明盡管防御導彈及來襲導彈的速度是實時變化的，但是依然能夠對來襲導彈進行攔截。但是，由圖6可以看出，在防御導彈發射起始階段，防御導彈的指令加速度存在更大的振蕩，驗證了假設的正確性，即起始階段目標機與防御導彈之間的視線LOSTD的轉動角速率極易受防御導彈運動的影響，這是引發防御導彈指令加速度振蕩的原因。

防御導彈指令加速度的振蕩不可避免地會影響系統的性能，因此對防御導彈指令加速度的振蕩進行抑制是十分必要的。考慮到在初始階段，目標機與防御導彈之間距離很近，防御導彈離來襲導彈較遠對整個導引律在初始階段的影響可以忽略。因此，可以將式(5)修改為:

防御導彈軸向加速度分解如圖7所示。

圖7 防御導彈軸向加速度分解圖Fig.7 Defense missile axial acceleration diagram

由圖7可知，防御導彈的軸向加速度有垂直于視線LOSTD方向(⊥LOSTM)的分量，并且其軸向加速度不可控，因此應對垂直于視線LOSTD方向的控制指令加速度 ac⊥LOS進行修正，則有:

綜上可知，修正后的防御導彈導引律為:

分別采用修正前后的導引律進行仿真，結果如表3及圖8、圖9所示。

表3 修正前后主動防御導引律的攔截時間及脫靶量Table 3 Interception time and miss distance before and after correction

圖8 修正前后的攔截軌跡Fig.8 Interception trajectories before and after correction

由表3、圖8可知，修正前后的導引律都能有效對來襲導彈進行攔截。

圖9 修正前后指令加速度及外角曲線Fig.9 Acceleration commands and exterior angleσ before and after correction

由圖9可知，引入修正量起到了有效改善主動防御導引律性能的作用。

3 結束語

針對主動防御問題，本文設計了一種基于雙視線角的比例-微分主動防御導引律，并在二維平面進行了仿真驗證。由于三維空間的運動軌跡可以分解至相互垂直的兩個平面內(水平和垂直平面)，因此二維平面內仿真驗證可以說明該方法的正確性。但是，本文的研究對象都是選用速度恒定的質點模型，相對于三自由度或是六自由度的飛機、導彈模型尚存在一定的差距。同時，本文的研究都是建立在對攻擊導彈的狀態信息以及導引律已知的情況下，而實際中攻擊導彈的狀態及導引律信息不可能完全已知，這些問題都是進一步需要進行的研究方向。

［1］ 張勇，楊軍.機載空空反導彈作戰系統效能仿真分析［J］.彈箭與制導學報，2006，26(1):51-53.

［2］ 王小平.導彈對抗條件下的空戰決策技術研究［D］.西安:空軍工程大學，2011.

［3］ 程建鋒.導彈對抗條件下駕駛員輔助決策與指引控制技術研究［D］.西安:空軍工程大學，2013.

［4］ 王斯財，南英，劉經緯.導彈迎擊時飛機的最佳逃逸策略研究［J］.航空兵器，2009(4):28-32.

［5］ Ashwini Ratnoo，Tal Shima.Line of sight guidance for defending an aircraft［R］.AIAA-2010-7877，2010.

［6］ Tal Shima.Optimal cooperative pursuit and evasion strategies against a homing missile ［J］.Journal of Guidance，Control，and Dynamics，2011，34(2):414-425.

［7］ 花文華，陳興林，宋超.主動防御協同自適應滑模制導律［J］.飛行力學，2012，30(1):66-70.

［8］ 劉哲，王小平，程建鋒，等.主動防御最優追蹤-逃逸導引律設計［J］.飛行力學，2014，32(5):432-436.

［9］ 馬明.論空空反導彈武器［J］.戰術導彈技術，2002(5):41-45.

［10］ Guelman M.Proportional navigation with a maneuvering target［J］.IEEE Transactions on Aerospace and Electronic Systems，1972，8(3):364-371.

［11］ Guelman M.Missile acceleration in proportional navigation［J］.IEEE Transactions on Aerospace and Electronic Systems，1973，9(3):462-463.