一種導彈導引律及參數的非線性MMAE辨識方法

王小平，蔡遠利，于振華，林秦穎，葉希貴，狄方旭

(1.西安交通大學 電子與信息工程學院，陜西 西安710049;

2.中航工業613研究所 光電控制技術重點實驗室，河南 洛陽471009;3.空軍工程大學 航空航天工程學院，陜西 西安710038)

0 引言

目前大多數關于飛機對抗導彈的最優軌跡優化問題的研究，所采用的方法和得到的結論均需要了解攻擊導彈的所有信息。然而，在實戰中往往對來襲導彈缺乏足夠的了解，難以完全掌握來襲導彈導引律、導引參數以及導彈本身等信息，因此對導彈的導引律、導引參數等進行辨識的研究具有重要的科學意義和工程價值。

對于上述問題，國內外公開的研究文獻相對較少。文獻［1］采用一種極大似然估計器實現了對某地空導彈PPN導引律參數的估計。文獻［2］通過一組導引律模型，采用Byesian理論計算似然函數的方法實現對導引律的辨識并進行軌跡優化。雖然上述方法在導彈的彈道特征比較明顯時可以有效估計出導引律參數，但對于前置角特性基本一致的同類導引律卻難以奏效。文獻［3］采用多模型自適應估計(MMAE)方法，在二維平面內，通過線性化導引律方程實現了導引律的辨識。

本文通過導彈三自由度質點模型與導引律相結合直接建模，建立導彈導引非線性模型集，研究采用基于UKF的MMAE算法，直接在三維坐標內實現對導彈導引律和導引參數的快速準確辨識。

1 數學模型

1.1 導彈模型建立

導彈可用三自由度質點模型表示為:

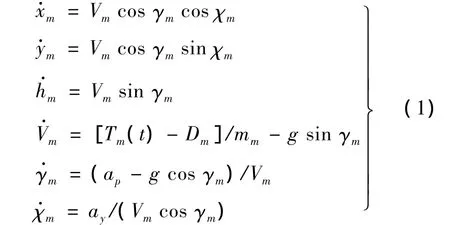
式中:狀態變量［xm，ym，hm，Vm，γm，χm］分別為導彈的三維坐標、速度、航跡傾角、航跡偏航角;Tm為導彈發動機推力;Dm為導彈受到的空氣阻力;ap，ay為縱向和側向加速度。考慮到導彈在目標搜索、制導以及導彈的實際響應慣性，通常將導彈俯仰和偏航加速度指令響應等效為一階模型，慣性時間常數設為τ，表達式如下:

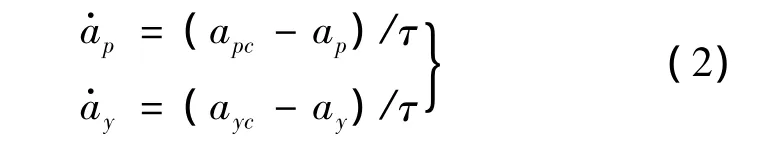
式中:apc和ayc分別為導彈的俯仰加速度指令和偏航加速度指令。對于不同的導引律，其生成方式也不同。一般情況下，在導彈的末制導狀態下，可以假設導彈的飛行速度保持常值，即將式(1)中的方程替換為:

由此，可以得到導彈狀態向量為:

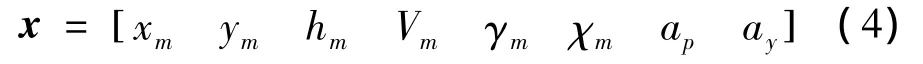
1.2 導彈導引律模型建立

考慮目前導彈采用的主流導引律情況，分別建立IPN，APN，OGL和PP導引律模型。

(1)IPN導引律:

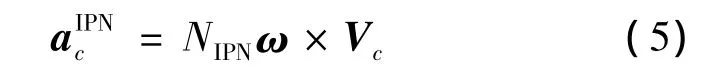
式中:NIPN為導引常數;ω為視線角速率;Vc為接近速度。

(2)APN導引律:

式中:NAPN為導引常數;at為目標加速度。

(3)OGL導引律:

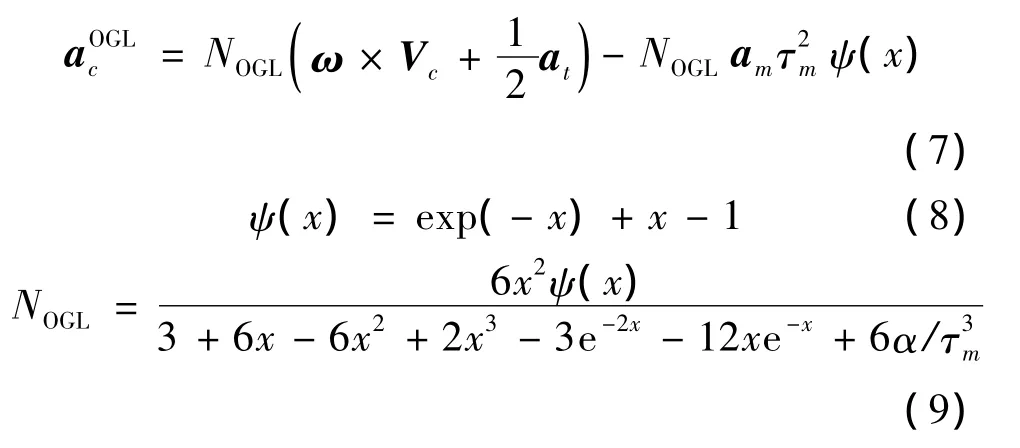
式中:NOGL為導引常數，由參數α決定;am為導彈的加速度;標準剩余機動時間

(4)PP導引律:

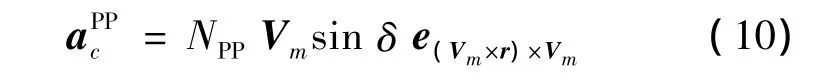
式中:NPP為導引常數為(Vm×r)×Vm方向的單位矢量。

2 非線性MMAE導彈導引律辨識算法

MMAE 方法最早由 Magill［4］提出，并由 Sims等［5］進一步完善而來，也是目前應用較為廣泛的一種估計方法。其優點在于可以實現精確的模型匹配和參數辨識，狀態估計精度高。為適應對抗條件下導彈大機動時的狀態估計及導引律和參數辨識，本文使用非線性導彈模型并利用UKF算法［6-8］構建了UKF-MMAE導引律辨識算法，其結構如圖1所示。

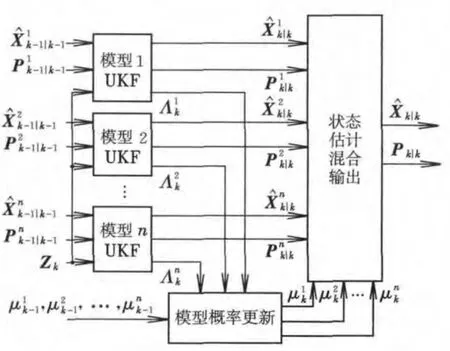
圖1 UKF-MMAE算法結構圖Fig.1 Algorithm structure of UKF-MMAE

算法核心思想是:根據導彈和導引律的非線性描述構建模型集，通過對模型集中的各個模型進行并行無色卡爾曼濾波(UKF)估計，并根據估計輸出與觀測數據的匹配情況確定各模型的權重(似然函數)，總估計輸出為各模型的輸出與權重乘積的組合，同時根據各模型的似然函數實現導彈導引律和參數辨識。該算法中主要包括有:MMAE模型集、并行UKF濾波、模型概率更新和狀態估計混合輸出。

2.1 MMAE模型集

對于MMAE算法，其模型集必須與實際模型集相一致，在此假設攻擊導彈導引律為上述4種導引律之一，并根據每種導引律的參數范圍，選擇特定的參數值，與導彈的三自由度非線性模型組合，構成MMAE算法的所需模型集。

2.2 UKF濾波算法

在UKF-MMAE中，各模型的濾波算法相同，均為UKF濾波算法，因此，在此僅給出第j個模型Mj的UKF濾波算法表達式。

(1)量測方程

各模型的量測方程均表示為:

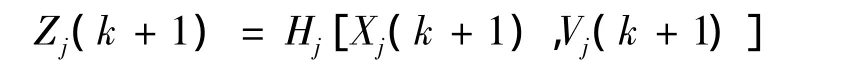
通過機載雷達對來襲導彈實現測量是在球面坐標系下的，通常可以測得飛機與導彈之間的距離r，目標的高低角e和方位角b。考慮到機載雷達的測量值均為導彈與飛機之間的相對關系，并且假設本機的位置和運動信息已知，可得:

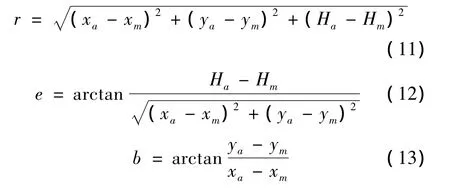
因此量測向量可表示為:

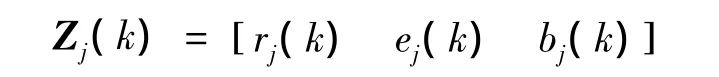
(2)UKF預測方程

首先在UT變換中，應用比例修正框架的比例對稱采樣［9］實現 Sigma點采樣，得到Sigma采樣點χj和權值聯合向量最后推得測量、測量協方差、狀態與測量協方差的預測方程，以及狀態向量和方差更新的方程如下:

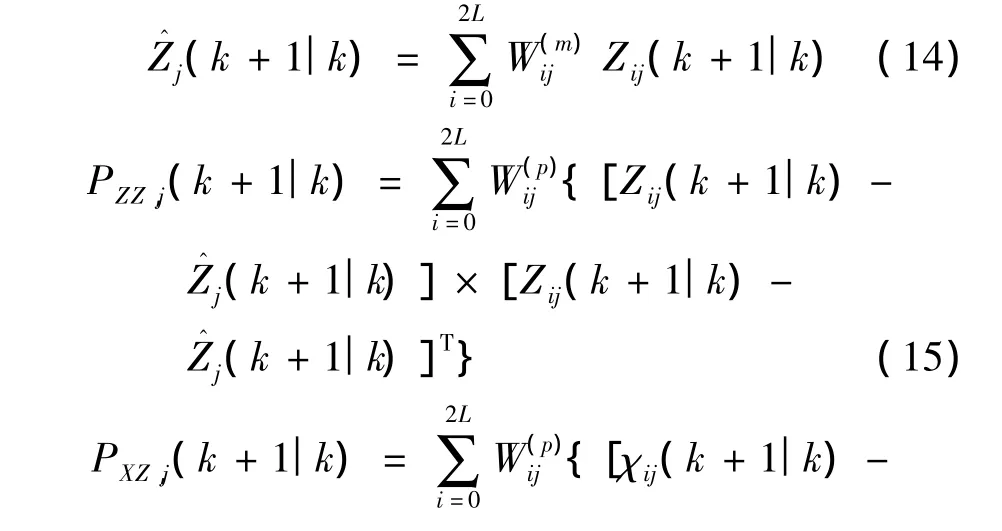
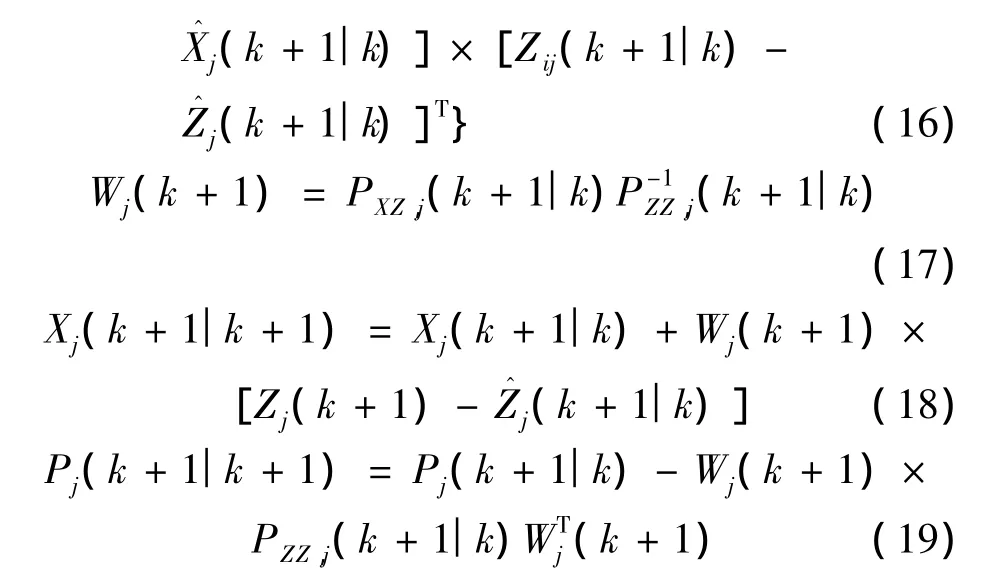
2.3 模型概率更新

根據上述的UKF濾波算法，可以得到模型集中各模型的預測輸出，并與實際量測信息比較得到預測誤差為:

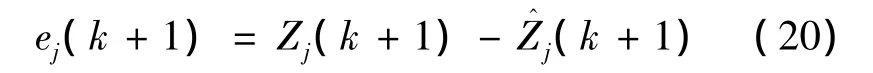
采用Gaussian density函數確定與第j個模型匹配的似然函數表達式如下:

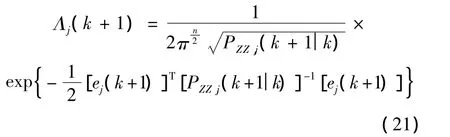
根據各模型的似然函數Λj(k+1)進行模型匹配概率的更新，得到各模型的預測概率:

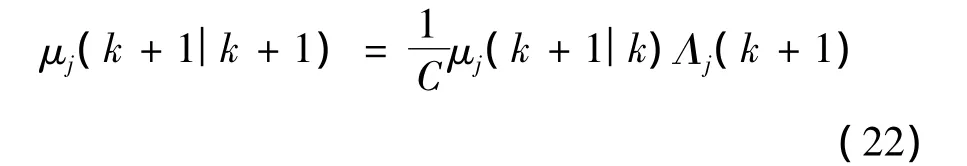
其中，歸一化系數C為:

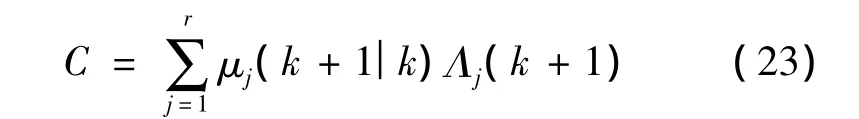
2.4 狀態估計混合輸出

在多模型估計器中，存在多個模型的估計輸出，在假設各模型匹配概率計算正確的前提下，則估計器的總輸出為:

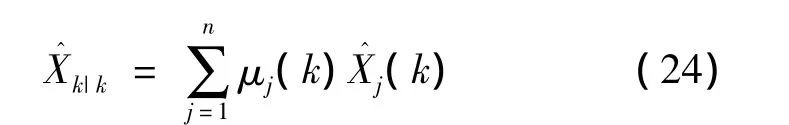
總的協方差陣:

3 導彈導引律辨識仿真

導彈的導引律辨識包括:確定導彈的導引律類型和確定導引律參數。在導引律參數中，需要辨識的增益包括 NIPN，NAPN，NOGL和 NPP。增益 NIPN，NAPN和NPP為常數;NOGL為時變參數，主要辨識其中的α。在此根據各參數的實際工作設定取值范圍，NIPN，NAPN分別取(3，4，4.5，5);NPP取(2，5，8，10);NOGL中的α 取(0，0.03，0.06，0.1)。導彈和飛機的初始狀態如表1所示。

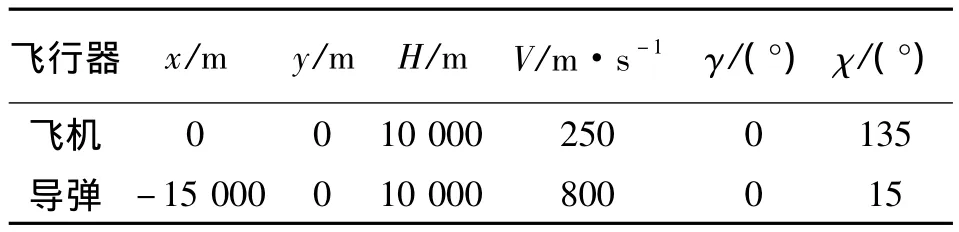
表1 飛機和導彈的初始狀態Table 1 Initial states of airplane and missile

離散節點間隔Δt=0.25 s，仿真步長ts=0.025 s，飛機采用固定機動飛行(迎角和滾轉角按正弦函數周期性變化)，導彈采用不同導引律進行攻擊狀態下得到的仿真數據，根據飛機和導彈的相對關系，計算出觀測數據，并人為加入測量噪聲，生成觀測數據:IPN導引律，導引參數NIPN=4時的辨識結果如圖2所示;APN導引律，導引參數為NAPN=4時的辨識結果如圖3所示;OGL導引率，α=0.1時對應導引參數NOGL的辨識結果如圖4所示;PP導引律，導引參數NPP=5時的辨識結果如圖5所示。

圖2 IPN辨識結果Fig.2 IPN identification results

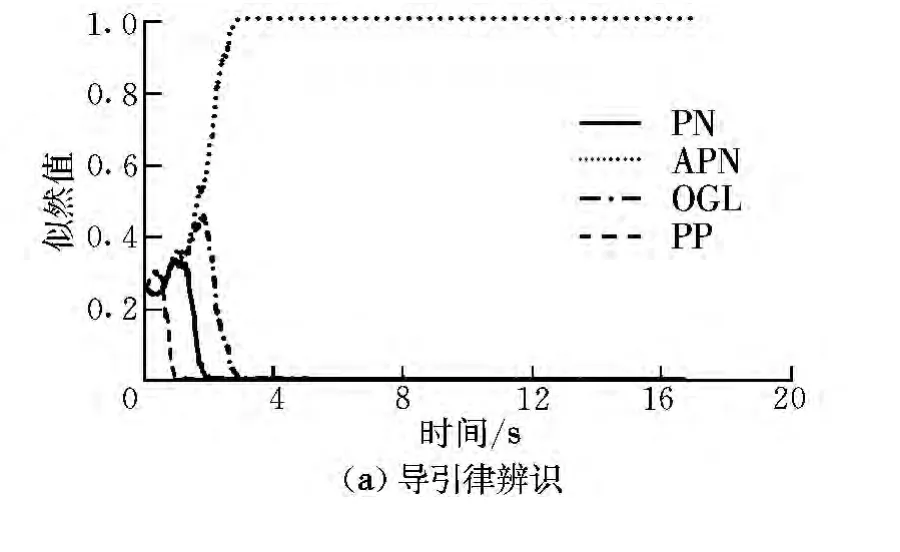
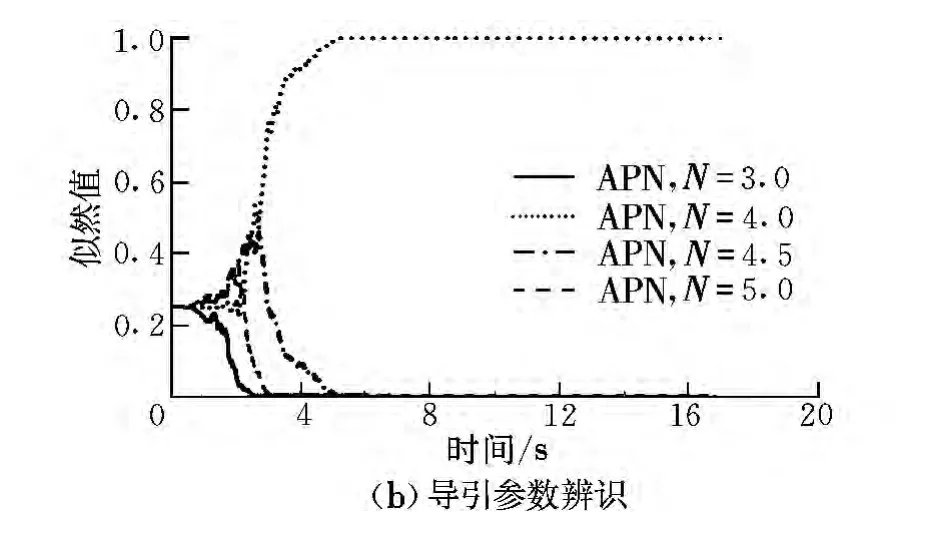
圖3 APN辨識結果Fig.3 APN identification results

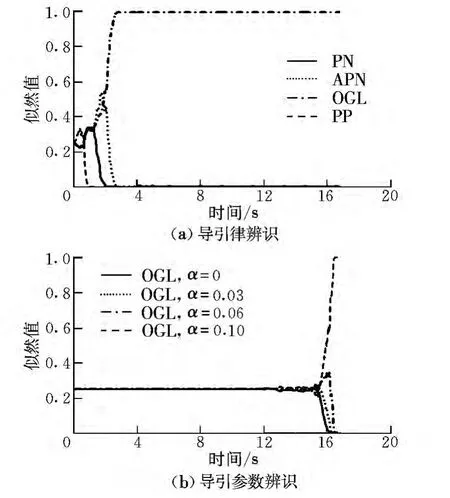
圖4 OGL辨識結果Fig.4 OGL identification results

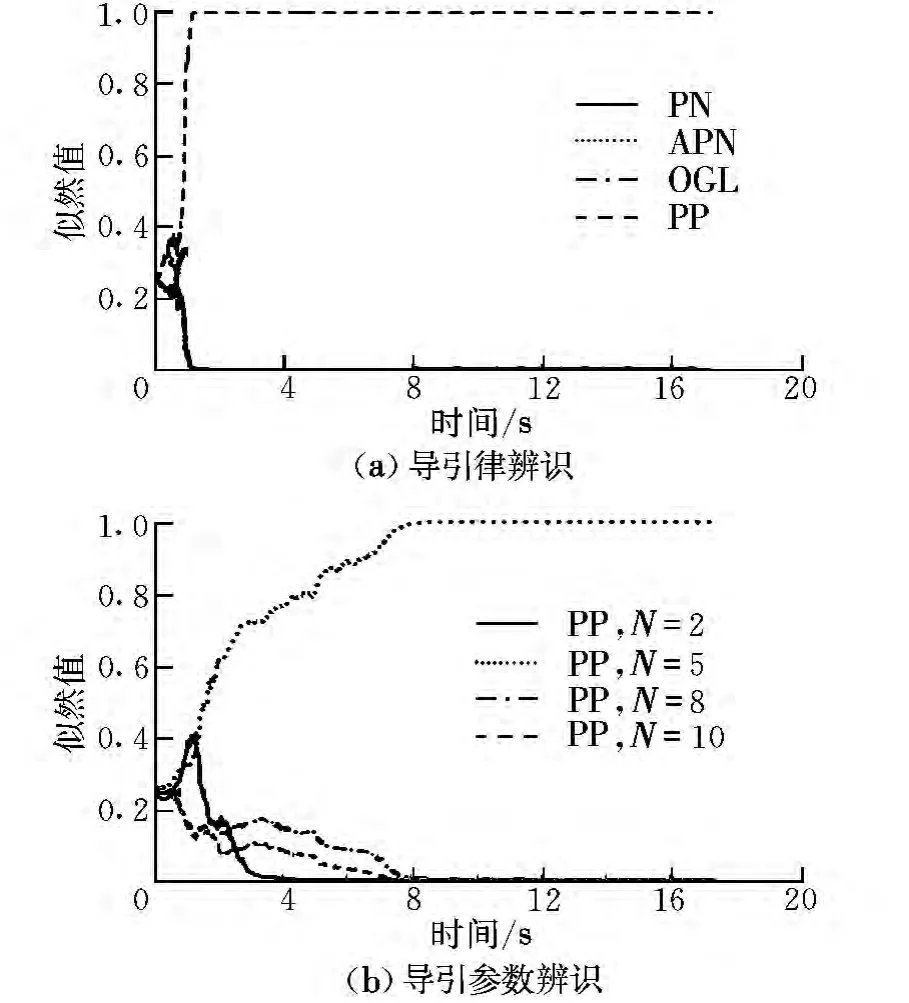
圖5 PP辨識結果Fig.5 PP identification results

由圖可知，采用MMAE算法，可以有效實現導引律類型的辨識。由于PP導引律與IPN，APN及OGL導引律差異較大，無論是排除還是認定，能夠在很短的時間內迅速被檢出。對于IPN，APN和OGL導引律，由于相互之間差異相對較小，檢出時間稍長，但均能在2.5 s內被有效識別。

在參數識別方面，APN參數識別的效果最好，能在4 s之內實現準確識別其導引參數;IPN參數識別時間在5 s之內;而對于PP導引律，其參數識別時間在4 s左右，且其匹配概率上升較為緩慢，主要原因在于當導彈和飛機距離較遠，且其LOS線與導彈速度矢量之間的夾角較小時，PP導引律產生的控制指令較小，導引系數對其影響較小，故導引參數確認過程較為緩慢。對于OGL導引律，由式(9)可知，當導彈與飛機距離較遠時，tgo時間比較大，且參數α一般很小，此時α對最終導引系數NOGL影響微弱，當導彈接近目標時，tgo時間減小，參數α對導引律的影響才逐漸顯現。因此，對于OGL參數α的識別只能在導彈遭遇目標前很短的時間內才能被有效檢測。

需要說明的是，對于導彈的導引律和參數辨識而言，特別是參數的辨識，只有在導彈的實際狀態與預期狀態存在差異，需要對導彈實施控制時，導引律和參數的差異性才能被充分顯現出來，即才能被有效識別或檢出。因此，要實現導引律和參數的辨識，飛機做一定的機動飛行是必要的前提條件。

4 結束語

本文針對導彈彈道特性接近情況下的導引律辨識問題，采用非線性模型、UKF濾波和MMAE相結合的思路，設計的導彈導引律和導引參數自適應算法，能夠直接在三維坐標內對主流的IPN，APN，OGL和PP導引律及其參數實現快速辨識。同樣，該方法可通過增加模型的方法來適應新的導引律，在導彈攔截、機動防御等方面具有實際應用價值。需要指出的是，該算法中存在兩點需改進之處:一是導彈勻速假設問題;二是為提高參數辨識精度需要增加估計器個數，進而會影響計算速度問題，需要在后續工作中進一步加強研究。

［1］ Lin L，Kirubarajan T，Barshalom Y.Pursuer identification and time-to-go estimation using passive measurements from an evader［J］.IEEE Transactions on Aerospace and Electronic Systems，2005，41(1):190-204.

［2］ Karelahti J，Virtanen K.Adaptive controller for the avoidance of an unknownly guided air combat missile［C］//The 46th IEEE Conference on Decision and Conrol.USA，2007:1306-1313.

［3］ Shaferman V，Shima T.Cooperative multiple-model adaptive guidancefor an aircraft defending missile［J］.Journal of Guidance，Control，and Dynamics，2010，33(6):1801-1812.

［4］ Magill T D.Optimal adaptive estimation of sampled stochastic processes［J］.IEEE Transactions on Automatic Control，1965，10(4):434-439.

［5］ Sims F L，Lainiotis D G.Recursive algorithm for the calculation of the adaptive Kalman filter weighting coeffcients［J］.IEEE Transactions on Automatic Control，1969，14(2):215-218.

［6］ Julier SJ，Uhlmann J K.A new extension of the Kalman filter to nonlinear system［C］//The 11th Int.Symp.on Aerospace/Defense Sensing，Simulation and Control.Orlando，Forida Academic Press，1997:562-569.

［7］ Wan E A，Merwe R，Nelson A T.Dual estimation and the unscented transformation［C］//Processing of the 2000 Conference:Advances in Neural Information Processing Systems 12.Washington，MIT Press，2000:600-672.

［8］ 潘泉，楊峰，葉亮，等.一類非線性濾波器-UKF綜述［J］.控制與決策，2005，20(5):481-494.

［9］ Wan E A，Van D R.The unscented Kalman filter，in Kalman filtering and neural network［M］.USA:John Wiley＆Sons，Inc.，2002.