一類延遲微分方程Rosenbrock方法的數(shù)值Hopf分支
岳 雙,張永坡,馮 雪
(空軍航空大學(xué)基礎(chǔ)部,吉林長春130022)
1 提出問題
延遲微分方程是泛函微分方程的一個重要分支,近年來很多學(xué)者研究了常微分方程的離散化格式對原連續(xù)的系統(tǒng)動力學(xué)性質(zhì)的保持性,而對延遲微分方程相關(guān)內(nèi)容的研究較少.英國V.Wulf等采用了Poincaré規(guī)范形進(jìn)行計算[1],目前很多學(xué)者將這種方法應(yīng)用到各種模型中.張春蕊等證明了顯式Euler方法對一類二維延遲微分系統(tǒng)Hopf分支結(jié)構(gòu)的保持[2];王秋寶等研究了Runge-Kutta方法對一類延遲微分系統(tǒng)Hopf分支性質(zhì)的保持[3-4].
考慮如下時滯為τ的延遲微分方程(其中時滯τ>0,y∈Rd,是連續(xù)的初始函數(shù)):
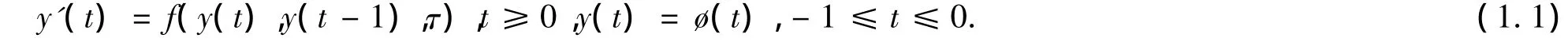
本文將討論延遲微分系統(tǒng)(1.1).
將S級Rosenbrock方法:

應(yīng)用于系統(tǒng)(1.1),得到數(shù)值離散格式:
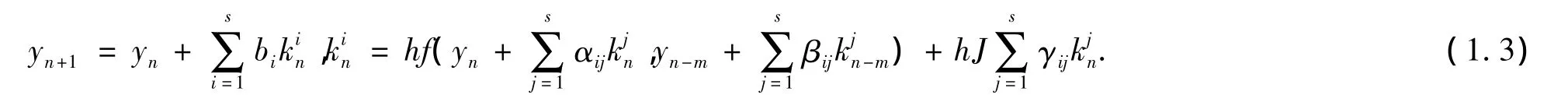
下列條件將保證在τ=τ*處系統(tǒng)(1.1)的零平衡點(diǎn)經(jīng)歷一個非退化的Hopf分支[1].
(A1)f(0,0,τ)=0,當(dāng)τ∈N(τ*),N(τ*)是τ*的一個鄰域(條件(A1)保證了對所有的τ∈N(τ*),系統(tǒng)(1.1)的零點(diǎn)是平衡點(diǎn));
(A2)當(dāng) τ∈ N(τ*)時,對于函數(shù) f(x,y,τ)有
(A3)系統(tǒng)(1.1)在零點(diǎn)處的線性化的特征方程為(記μ=lnλ)
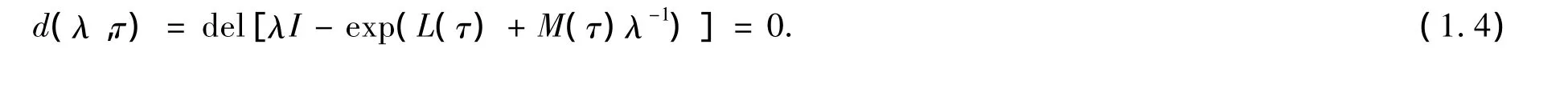
當(dāng) τ∈ N(τ*)時,該特征方程有一對簡單的復(fù)共軛根 λ1,2= η(τ)e±iω(τ),并且存在0 < r < 1,使得所有其他根的模小于r;
(A4)對于 τ= τ*,有 η(τ*)=1,ω(τ*)= ω0> 0;
(A5)η'τ(τ*)> 0;
(A6)非退化條件成立.
若假設(shè)(A3)~(A6)成立,則系統(tǒng)(1.1)經(jīng)歷一個Hopf分支;則零解在τ經(jīng)過τ*時不是漸進(jìn)穩(wěn)定的(不失一般性,當(dāng)從左到右時,由條件(A5)可知有一個小振幅的吸引周期軌出現(xiàn)(超臨界Hopf分支)或一個排斥軌消失(下臨界Hopf分支)).
2 數(shù)值Hopf分支的分支方向與分支不變曲線的穩(wěn)定性
延遲微分方程Hopf分支分析的方法來自于Hassard等人眾所周之的思想[5].令τ=s+τ*,則可將系統(tǒng)(1.2)變換為 C=C([- 1,0],Rd)上的延遲微分方程.
定義

由文獻(xiàn)[6]可知,Re c1(τ*)的符號確定了分支周期解的穩(wěn)定性.
3 數(shù)值試驗(yàn)
為了驗(yàn)證得出的結(jié)論,考慮下列方程[7]:
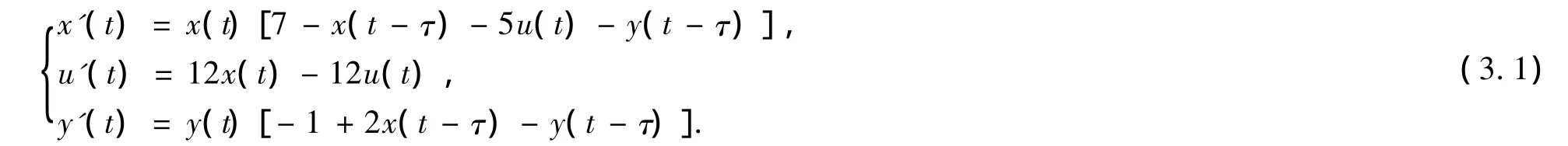
此系統(tǒng)有唯一的正平衡點(diǎn)E*(1,1,1),可求出分支點(diǎn)τ*=1.0663,且有
(1)當(dāng)τ<τ*時,E*是穩(wěn)定的(圖1);(2)當(dāng)τ經(jīng)過τ*時,E*失去穩(wěn)定性,經(jīng)歷Hopf分支,分支出周期解,且Hopf分支是超臨界的,分支方向?yàn)棣樱睛?,且分支周期解是穩(wěn)定的(圖2).
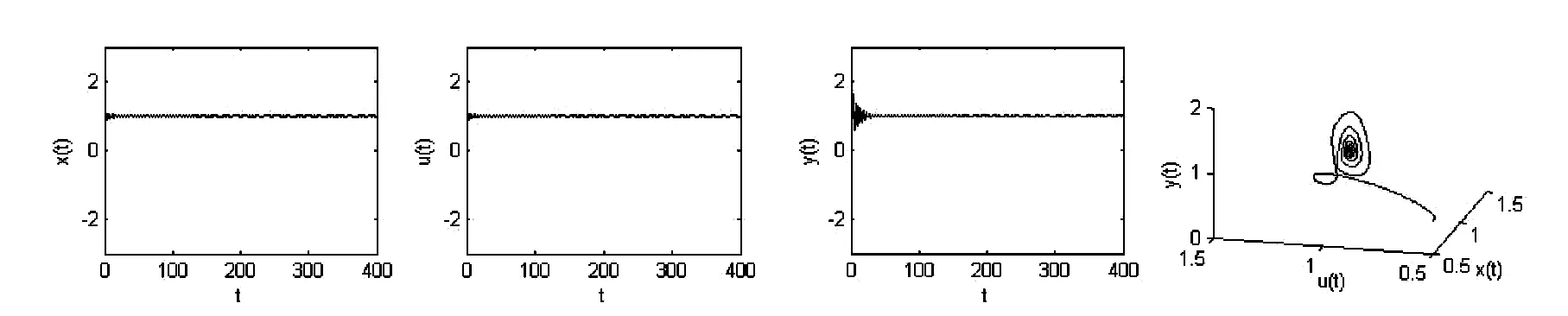
圖1 τ=0.9 < τ*,平衡點(diǎn)E*(1,1,1)是漸近穩(wěn)定的

圖2 τ=1.2>τ*,平衡點(diǎn)E*(1,1,1)處產(chǎn)生分支周期解,并且是漸進(jìn)穩(wěn)定的
將2級2階Rosenbrock方法應(yīng)用到方程(3.1),其中,b1=0,b2=1,2,經(jīng)計算可知其滿足定理2.6的條件.得到相圖如圖3與圖4所示,數(shù)值Hopf分支保持了分支方向與分支不變曲線的穩(wěn)定性.
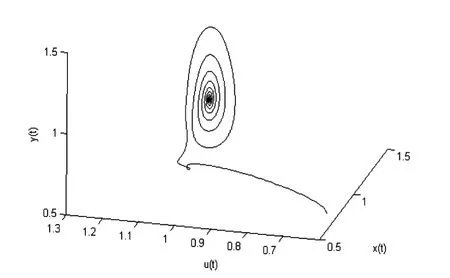
圖3 應(yīng)用2階Rosenbrock方法,τ=0.9 < τ*,h=0.01 時平衡點(diǎn) E*(1,1,1)漸進(jìn)穩(wěn)定
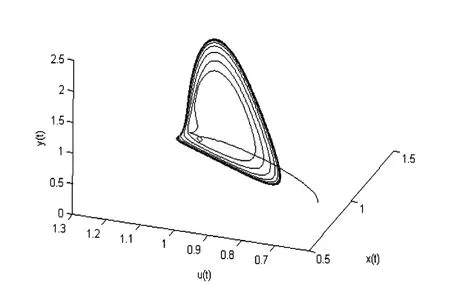
圖4 應(yīng)用2階Rosenbrock方法,τ=1.2 > τ*,h=0.01時平衡點(diǎn)E*(1,1,1)處產(chǎn)生分支周期解,并且是漸進(jìn)穩(wěn)定的
[1]Ford NJ,Wulf V.Numerical Hopf bifurcation for the delay logistic equation[R].Manchester Center for Computational Mathematics:Technical Report,1998,323.
[2]Zhang Chunrui,Liu Mingzhu,Zheng Baodong.Hopf bifurcation in numerical approximation of a class delay differential equations[J].Appl Math Comput,2003,146:335 -349.
[3]Qiubao Wang,Dongsong Li.Numerical Hopf bifurcation of Runge – Kutta methods for a class of delay differential equations[J].Chaos,Solitons and Fractals,2009,42:3087 -3099.
[4]M.Z.Liu,Qiubao Wang.Numerical Hopf bifurcation of linear multistep methods for a class of delay differential equations[J].Applied Mathematics and Computation,2009,208:462 -474.
[5]Hassard BD,Kazarinoff ND,Wa YH.Theory and applications of Hopf bifurcation[M].Cambridge:Cambridge University Press,1981.
[6]Wulf V,F(xiàn)ord NJ.Numerical Hopf bifurcation for a class of delay differential equations[J].J Comput Appl Math,2000,115:601-616.
[7]馬占平.幾類非線性生物數(shù)學(xué)模型的動力學(xué)行為研究[D].蘭州:蘭州理工大學(xué),2008.

