改進遺傳算法在應急物資調運模型中的應用

宋樹洋

（北京航空航天大學經濟管理學院，中國 北京100000）

應急物資的運輸與配送問題是應急物流主要研究的問題之一，它也是應急物流中最為關鍵的一個環節，而在一般情況下，應急物資調運問題就會轉化成一般的車輛路徑問題。車輛路徑問題是一個典型的組合優化問題，求解十分困難，截至當下，僅有一些相對較小規模的問題能夠保證被求解到精確的最優解。各國的學者通過大量的實踐和理論證明得出結論，精確算法在求解大規模VRP問題時非常不適合，而啟發式算法在求解這類問題時顯示出非常大的優勢，并成為近年來此領域應用最多的方法。其中遺傳算法以其優秀的尋優能力為眾多學者所青睞。

1 遺傳算法

遺傳算法(Genetic Algorithm，簡稱GA)是由Holland教授首先提出的，它是一種建立在群體遺傳學基礎和自然選擇上的隨機、并行搜索算法。求解車輛調度問題，使用GA搜索算法十分理想，但使用GA算法時面臨的一個難以解決的問題就是如何防止其“早熟”收斂。

在遺傳算法提出以來，來自世界各地的眾多學者提出了多種方法提高GA的性能：Rudolhp G提出為保證算法的收斂性，使用精英選擇策略保持群體中最好個體的方法[1]；馬欣等提出了PEGA算法，即使用單親進化的遺傳算法，它提高算法收斂速度的方法，是利用來自父體有效邊的信息，保留使用最小邊，這樣來進行個體的進化[2]；馬均水等提出大變異策略，這個策略可以表述為，如果某一代里的大多數個體集中在了一起，此時使用一個較大的變異概率（遠大于通常）執行一次變異操作，這樣使之獨立產生多個新個體，可以讓整個群體脫離早熟[3]；以上方法只解決了算法部分問題，而且采取的改進方式比較復雜，一般以高運算量并降低算法效率為代價解決遺傳算法過早收斂的問題。

遺傳算法優化分析：

早熟收斂一直是遺傳算法中存在的主要問題，算法一旦出現早熟收斂，將無法得到問題的最優解，這個問題主要原因是遺傳算法自身的優化能力有限，不得不需要多次迭代才能夠找到最優解，迭代過程中發生早熟將很難跳出。本文主要研究如何避免早熟收斂問題，下面將在交叉概率一定的(pc=0.8)的前提下進行研究討論。

1）變異算子的改進

對于遺傳算法易“早熟”的問題，其中主要原因之一是遺傳算法中最重要的遺傳算子——交叉算子使群體中的染色體具有局部相似性，從而會導致搜索停滯不前，因此變異算子的存在就變成克服算法早熟的最有效手段。

2）傳統變異算子的缺陷

定義1 在優化問題求解過程中得到的最優解，其對應染色體上的每個基因稱為這個染色體基因位上的有效基因。

定義2 種群中，染色體同一個基因位上的等位基因具有多樣性，即染色體相同的基因位上既有“1”又有“0”，或者說在某一個基因位上，基因全為“1”(或“0”)的概率P(“1”)(或P(“0”))為：

P（“0”）或P（“1”）＝0 （1）

J.Craig Potts等人的研究得出結論，在GA搜索中，在遺傳算法運行過程中發生早熟收斂的原因主要是有效等位基因缺失[4]。選擇策略的目的是在于加快基因的收斂過程，但是交叉算子作用于個體卻不可能產出新的基因，所以這無法避免地會使得在特定基因位上的某一類基因比例下降，最終會導致這個基因位上可能的有效基因的缺損。因此，為了預防早熟收斂，在不知道有效基因位的情形下，如果變異算子可以讓染色體統一基因位上保持等位基因的高多樣性，那么將極大地防止有效基因的缺失，進而在最大程度上避免遺傳算法運行過程中的早熟收斂。

定理1 一般方法使用的變異算子沒有辦法保證保持染色體同一基因位上等位基因的多樣性。

證明：在一個種群規模為N的種群中，如果假設在染色體的第j個基因位上有n1個“0”和n2(n2=N-n1)個“1”，那么這個基因位上的全部基因經過變異操作（取反操作）后變為同一個基因的概率為：

此式與式（1）矛盾。

3）二元變異算子

一般來說，一般的變異算子作用是進行的是一元操作（取反操作），即是操作數需要且僅需要一個基因。如果染色體是由二進制字符串組成的，對于此類染色體，我們可以在遺傳算法搜索中引入數字技術里的二元邏輯算子，優化傳統的變異方式，即產生了二元的變異算子：同或/異或。

此種變異操作與傳統的取反變異有所不同，這種變異操作中需要兩個個體（染色體）參與，例如：

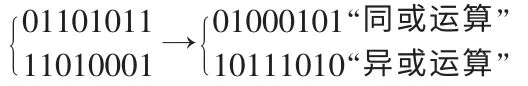
從邏輯上容易知道，在這個運算之后得到的兩種邏輯狀態是互補關系，即如果一個為“0”，另一個一定為“1”。換句話說在一個基因位上的基因經過變異操作之后，這個基因位上至少有一個“0”和一個“1”同時存在，但是并不會出現都是“0”或者都是“1”的情況。

基于二元變異算子的遺傳算法流程與原遺傳算法流程相同，只在變異操作時有所區別。

2 應急物資調度模型

2.1 問題的提出

應急資源的調度需要考慮的問題有很多，其中包括運輸工具的調度、運輸路線的設計，還有資源調度的速度和效率。突發事件發生后，如果造成了大面積的受災，救災物資需求點的數量很多，那么在短時間內制定出合理的物資配送計劃將會十分困難。

應急資源調度問題可以抽象為圖1所示：

圖1 震后應急資源調度問題抽象模型

2.2 問題情景描述

假設中國西南部某地發生了一定強度的地震，地震地帶處于山地丘陵地形內，震后造成交通線路阻斷，圍繞震中形成了幾個受災較為嚴重的區域，區域內交通能力恢復迅速，區域與區域之間處于半隔離狀態。處于各受災區域的政府救助力量迅速組織人員和工具分別進行難民的搜尋和治療，并以最快的速度恢復通信能力，與上一級政府組織取得聯系并發出求救信息。上級地震災害救助領導組織匯集各區域需求，利用空中設備(直升機)將救災物資空投至各區域，其中包括醫藥、食物、飲用水、救災車輛及工具等具體物資，另各救災區域內的救災應急小組抓緊組織收集可利用的機動性運輸工具，在各區域內形成配送中心，根據各需求點需求進行救災物資配送和傷員運輸。

2.3 模型的建立

2.3.1 模型的假設條件

假設一：應急資源調度中心與各物資需求點、各物資需求點之間的運輸距離已知，可以作為常數。

假設二：受災地點及各應急資源調度中心根據其地理位置及交通便利情況完成最優區域劃分，形成局部地震救災單元，單元區域內可以以最快速度進行物資分配及救災響應。各單元地震災區資源運輸費用有限可加，總和為地震總災區資源調度費用。

假設三：救災物資運送車輛所在停車場與應急物資調度中心之間的距離可以忽略不計。

假設四：所有的需求點之間都可以相互通行，即此路徑網絡是完全路網。

假設五：所有的受災地點的資源需求，在時間和數量方面都能夠得到滿足。

假設六：物資從調運車輛上卸載的時間忽略，不予計算。

2.3.2 問題的數學模型描述

應急資源車輛調度問題的數學模型可以概述如下：對于單一地震災害救助單元，把各物資需求節點和應急資源調度中心組成一個圖G(V,E)，其中V是圖中所有節點的集合，Vo∈V是應急資源調度中心，其余節點為物資需求節點；E為圖中所有邊的集合，eij∈E為節點i，j之間的邊，圖G為無向圖，即邊eij是無方向的。有n個受災地向救災指揮中心請求物資配送，物資儲備中心與受災節點、受災節點之間的廣義運輸費用(距離)為Cij(i，j=0，1，2，…，n)，物資儲備中心編號為0，受災節點編號為1到n，要求為各地震應急救助區域指派運輸車輛k，并確定車輛運輸路線，使得總運輸費用最低。

對于模型圖中的每條弧(i，j)(i≠j)和車輛k定義變量Xijk：

應急資源調度模型如下：

目標函數：

以上數學模型中各表達式含義如下：

式（3）此式為目標函數，其表示總的路徑代價(運輸費用、距離或時間)最低；

式（4）保證了有且僅有一輛物資配給車輛從物資配送中心出發；

式（5）保證了每個物資需求點凈流量為0；

式（6）保證了有且只有一輛物資配給車輛最終回到調度中心。

2.4 模型求解

根據前面已經建立的應急物流車輛調度數學模型，可將此問題進一步描述如下：在各地震救災單元區域內，從配送中心派出車輛進行救災，每一輛車可為若干受災點載送物資，車輛行駛路徑應保證是距離最短的那條，最終要求出總消耗最低的路徑線路和最低費用(距離)。

2.4.1 求解步驟描述

遺傳算法優化算法(GA-plus)在求解應急資源調度問題時的基本步驟如下：

Step1：設定初始參數。主要是遺傳迭代次數、初始種群大小、交叉和變異概率；

Step2：隨機產生初始種群，利用適應度函數計算種群適應度；

Step3：根據適應度按輪盤賭方法和最佳個體復制選擇下一代染色體；

Step4：根據交叉概率，對染色體（候選解）進行順序交叉操作；

Step5：根據變異概率，對染色體（候選解）進行變異操作(二元變異)；

Step6：產生新的種群，利用適應度函數計算種群適應度，記錄新種群中的最佳個體；

Step7：判斷是否滿足遺傳算法迭代次數，若滿足則停止并輸出優化結果，否則轉Step2對新種群繼續操作。

2.4.2 案例分析

本文采用Matlab編程，對有30個節點、50個節點和75個節點三種情況進行試驗分析。

（1）30節點時

各算法參數設置為：

GA迭代步數為2000，種群規模為100，交叉概率為0.8，變異概率為0.2；

GA-plus迭代步數為2000，種群規模為100，交叉概率為0.8，變異概率為0.2。

（2）50節點時

各算法參數設置為：

GA迭代步數為3000，種群規模為150，交叉概率為0.8，變異概率為0.2；

GA-plus迭代步數為3000，種群規模為150，交叉概率為0.8，變異概率為0.2。

（3）75節點時

各算法參數設置為：

GA迭代步數為7000，種群規模為200，交叉概率為0.8，變異概率為0.2；

GA-plus迭代步數為7000，種群規模為200，交叉概率為0.8，變異概率為0.2。

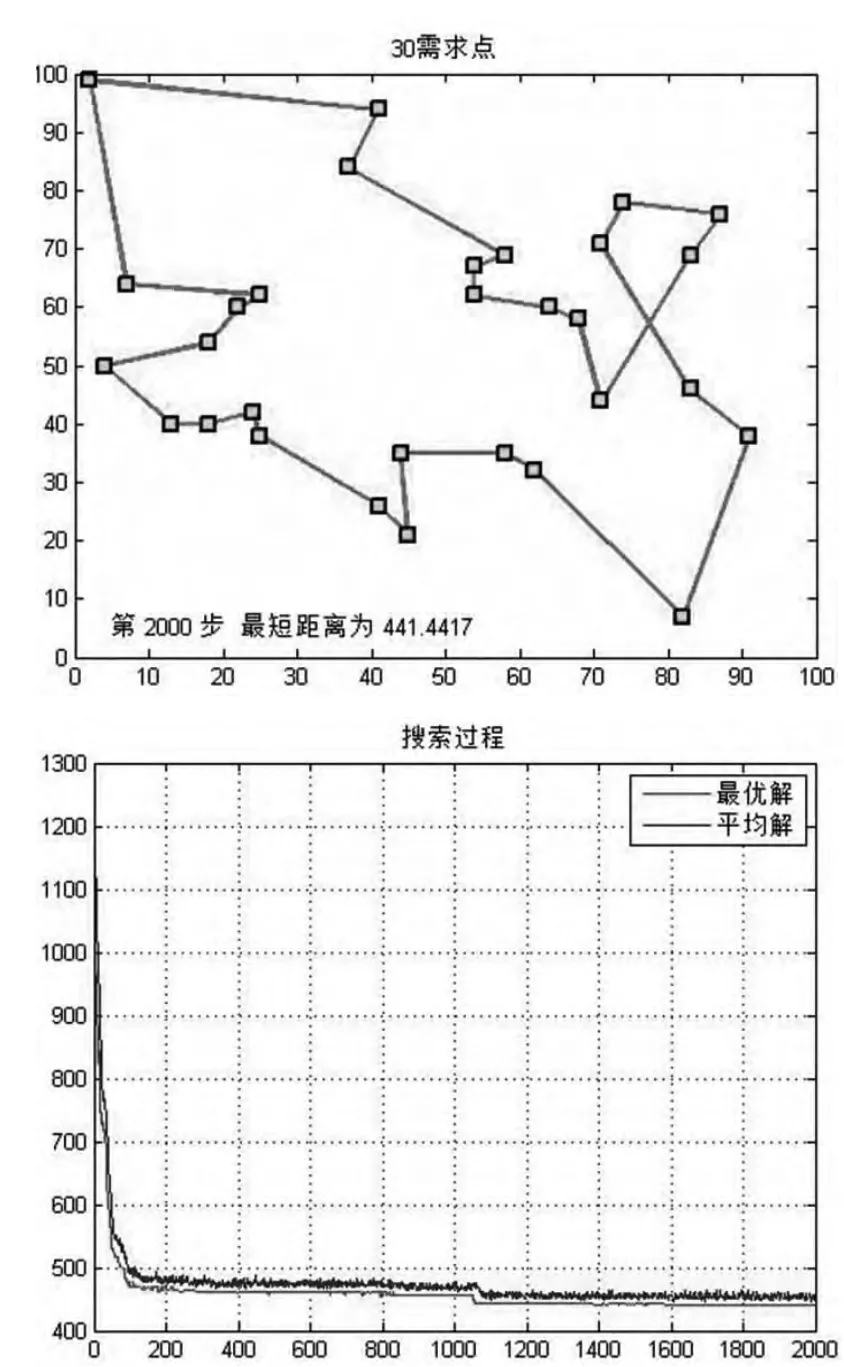
圖2 GA搜索結果

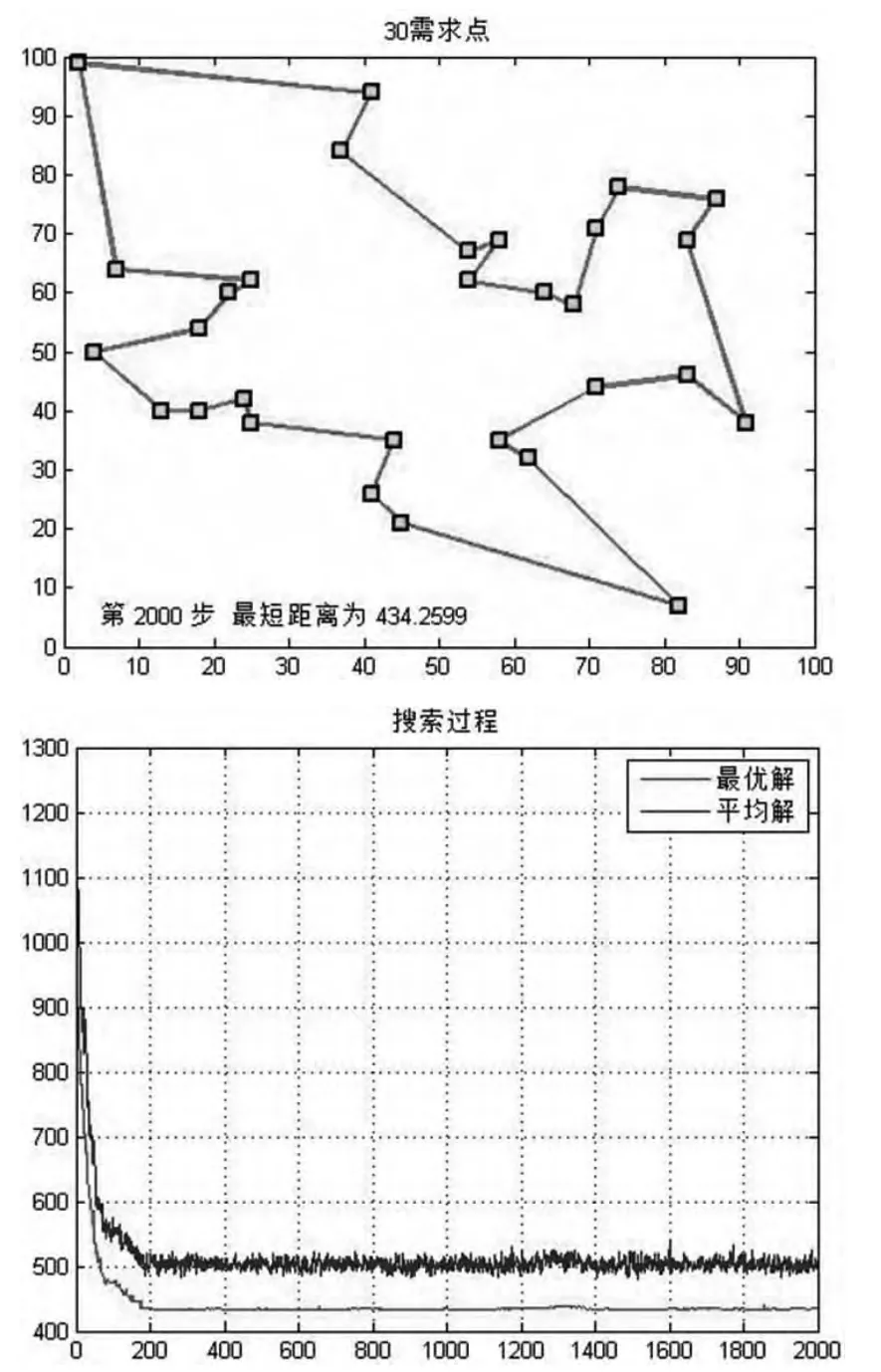
圖3 GA-plus搜索結果

圖4 GA搜索結果

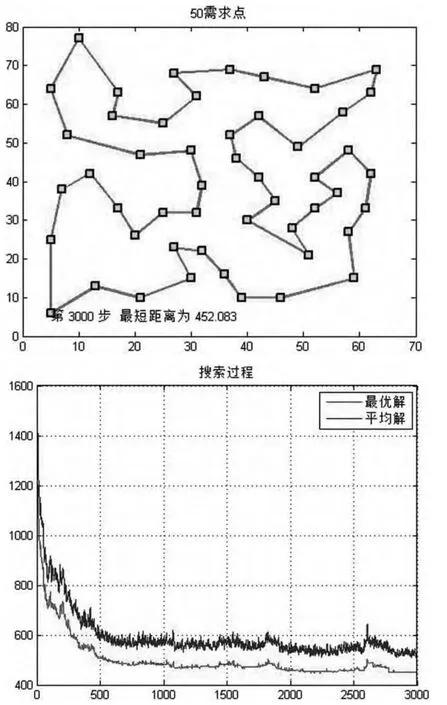
圖5 GA-plus搜索結果

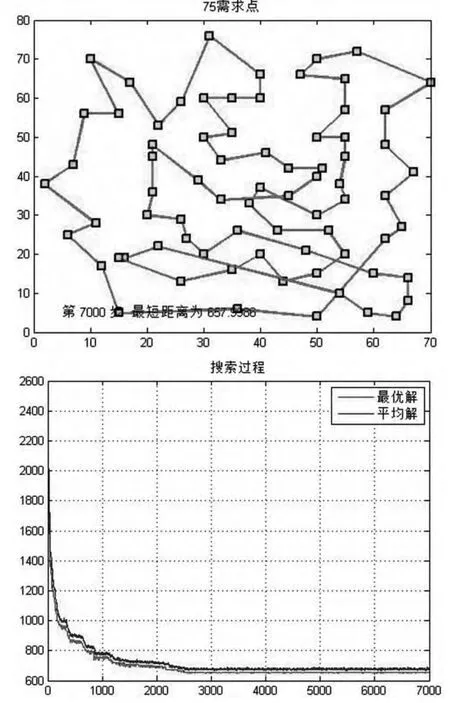
圖6 GA搜索結果

圖7 GA-plus搜索結果

3 結束語

通過實驗過程以及以上圖示結果，可以對GA-plus優化方法得出以下結論：

（1）GA-plus的全局優化度相對較高，最終解顯示出更優水平，并且平均優化度也比較高；

（2）GA-plus的魯棒性強，趨于優化解的概率較高；

（3）GA-plus的計算時間較長，在算法效率上有待提高，但在一定程度上克服了過早收斂的早熟問題。

本文針對應急物資調運問題建立了數學模型，對模型求解過程中使用的啟發式算法進行了優化和改進，實驗結果表明改進后的算法增強了對問題的求解能力，一定程度上克服了算法過早收斂的問題。本文對于應急物資調運問題的研究對于實際問題也具有借鑒意義

［1］Rudolph G. Convergence analysis of canonical genetic algorithms [J]. Neural Networks, IEEE Transactions on, 1994,5(1):96-101.

［2］馬欣,朱雙東,楊斐.旅行商問題(TSP)的一種改進遺傳算法[J].計算機仿真,2003,4:36-37.

［3］馬鈞水,劉貴忠.改進遺傳算法搜索性能的大變異操作[J].控制理論與應用,1998,15(3):404-408.

［4］Potts J C, Giddens T D, Yadav S B. The development and evaluation of an improved genetic algorithm based on migration and artificial selection [J]. Systems,Man and Cybernetics, IEEE Transactions on, 1994,24(1):73-86.