廣義經驗模態分解性能分析與應用

第一作者鄭近德男，博士生，1986年生

通信作者程軍圣男，博士，教授，博士生導師，1968年生

廣義經驗模態分解性能分析與應用

鄭近德,程軍圣,曾鳴,羅頌榮

(湖南大學汽車車身先進設計制造國家重點實驗室，長沙410082)

摘要：針對經驗模態分解(Empirical Mode Decomposition，EMD)的均值曲線采用三次樣條擬合而容易引起包絡過沖和不足等缺陷，相關學者提出了許多改進均值曲線的變種EMD方法，取得了一定的效果。廣義經驗模態分解(Generalized EMD，GEMD)方法綜合了多種改進EMD方法，通過定義不同的均值曲線對信號進行逐階篩分，從得到的每一階分量中選取最優作為最終的廣義內稟模態函數(Generalized Intrinsic Mode Function，GIMF)，由于每一階的GIMF分量都是最優的，因此相較于EMD等單一均值曲線篩分方法，GEMD分解結果也是最優的。論文對GIMF分量準則進行了改進以及對GEMD性能進行了分析，并將GEMD應用于仿真和實測信號的分析，結論表明GEMD分解是完備的和正交的，有比EMD更強的分解能力，而且適合機械振動信號的處理和故障診斷。

關鍵詞：經驗模態分解；廣義經驗模態分解；局部特征尺度分解；分解能力；故障診斷

收稿日期：2013-09-12修改稿收到日期：2014-01-09

中圖分類號:TH165+.3; TN911文獻標志碼：A

基金項目：973項目

基金項目：北京理工大學基礎研究基金(20120142009)

Performance analysis and application of generalized empirical mode decomposition

ZHENGJin-de,CHENGJun-sheng,ZENGMing,LUOSong-rong(State key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China)

Abstract:Aiming at that the mean curve defined in empirical mode decomposition (EMD) fitted with cubic spline may cause envelope overshoot and undershoot, many improved EMDs for improving the mean curve are proposed and some good effects are achieved. Generalized empirical mode decomposition (GEMD) integrates several improved EMD methods and selects the best component from components obtained by sifting different mean curves in each rank as the final generalized IMF (GIMF). Since the GIMF is the best in each rank, the corresponding results of GEMD are also the best. Here, GEMD was introduced firstly and then an improved criterion of GIMF was developed. Furthermore, GEMD was employed to analyze simulated and actual mechanical vibration signals. The results showed that GEMD is complete and orthogonal, it has a better capacity of decomposition than that of EMD, it is suitable for mechanical fault diagnosis as well.

Key words:EMD; GEMD; local characteristic-scale decomposition; capacity of decomposition; fault diagnosis

經驗模態分解(Empirical Mode Decomposition，EMD)是由Huang等[1-3]提出的一種自適應的數據處理方法。EMD方法通過定義瞬時頻率具有物理意義的內稟模態函數(Intrinsic Mode Function，IMF)，同時定義一種基于包絡的均值曲線，通過從原始信號中不斷分離出包絡均值曲線，即執行篩分過程，將原始信號分解為若干個IMF分量和一個剩余項之和。

由于原EMD方法中均值曲線定義為上、下包絡線的均值，其中上、下包絡線分別由三次樣條擬合極大值和極小值而成，因此，不可避免地會產生欠包絡和過包絡以及擬合誤差等問題。Chen等[4]提出了用B樣條代替三次樣條，以及Peel等[5-6]等提出用有理樣條取代三次樣條，這兩種改進三次樣條插值的方法雖然克服了三次樣條帶來的問題，但同時又引入了其它參數，且由于極值點是固定的，對大部分信號上述兩種分解方法的效果不是很明顯。蓋強和鄒巖崑等[7-8]提出的局域波分解方法提出了兩種新的均值曲線的定義方法，新的均值曲線避開了上下包絡線的定義，直接由數據的極值點定義均值曲線，且只采用一次三次樣條擬合，因此節約了計算時間和提高了計算速度。FREI等提出了一種新的時頻能分析方法——本征時間尺度分解(Intrinsic Time-scale Decomposition， ITD)，ITD基于極值的特征尺度和數據本身線性變換，提高了計算速度，避免了擬合誤差以及端點效應向數據內部的擴散影響，然而ITD分解由于采用線性變換，會導致得到的分量出現波形失真。最近，筆者[9]提出了另一種時頻分析方法——局部特征尺度分解方法(Local Characteristic-scale Decomposition， LCD)，LCD克服了ITD的不足，給出了一種新的均值曲線定義，然而LCD方法本質上也是EMD和ITD的變形方法。

上述改進的EMD方法本質上是對EMD均值曲線的改進，可能對某些信號而言，上述改進的方法在某一方面有一定的提高，而對另外一些信號原EMD方法仍具有其獨特的優勢；即使對同一個信號不同頻段的分量，可能改進的方法提取出的第一個分量較接近實際值，而對于第二個分量則可能是EMD提取的分量更接近實際值。當用上述方法分析實際信號時，無法判定哪種信號處理方法是最合適的和最優的。

基于上述考慮，綜合各種改進EMD方法的特點，筆者[10]提出了一種新的時頻分析方法——廣義經驗模態分解(Generalized Empirical Mode Decomposition, GEMD)。GEMD基于不同的均值曲線而定義，從高頻到低頻進行篩分，從每階得到的分量中選擇最優分量作為最終的廣義IMF(Generated IMF，GIMF)。再原始信號中減去該GIMF分量，并將剩余信號視為原始信號，不斷重復上述篩分過程，直到剩余信號是一單調或常函數，或者能量與原始信號相比可以忽略的函數。

本文詳細研究GEMD方法中GIMF分量的判據準則，在原帶寬準則的基礎上提出了一種瞬時頻率波動能量差準則；同時對GEMD分解的正交性和完備性進行了驗證，結果表明GEMD分解是正交的和完備的。最后，以兩個正弦信號疊加的混合信號模型為例，對GEMD方法的頻率分辨能力進行了研究，結果表明GEMD可分解信號范圍要大于EMD，能分解出EMD不能分解的兩頻率較為接近的信號的疊加信號，是一種具有良好性能的信號分解方法。

1廣義經驗模態分解

1.1均值曲線的定義

GEMD方法的關鍵是定義信號合理的均值曲線。然而難點在于，到目前為止，大部分關于均值曲線的定義都是經驗性的。綜合多種參考文獻，論文采用以下六種具有代表性的均值曲線的定義方法：

(1)包絡均值曲線(Envelop Mean，EM)，定義詳見EMD方法[1]。

(2)固有時間尺度均值(Intrinsic Time-scale Mean，ITM)定義參見文獻[11]。

(3)局部特征尺度均值(Local Characteristic-scale Mean，LCM)，定義參見文獻[9]。

(4)極值點中值均值(Extremum- midpoint mean，EMM)。

假設待分析信號為Yt(t≥0)，所有極值點為(τk,Yk)(k=1,2,…,M)，相鄰兩個極大值(或極小值)的中點可表示為

(1)

定義

(2)

再用三次樣條函數擬合和插值所有的(tk+1,Bk+1)即得到信號Yt的均值曲線。

(5)極值域均值(Extremum Field Mean，EFM)，定義參見文獻[7]。

(6)局部積分均值(Local Integral Mean，LIM)，定義參見文獻[12]。

(3)

其中:w(t) 是權重因子。 特別地，二者可定義為：

(4)

上述六種均值曲線的定義方法從不同的角度定義信號的均值曲線，大部分是經驗性的，它們的物理模型還有待于進一步驗證。

1.2GEMD

設待分析信號為x(t)，廣義經驗模態分解(GEMD)的主要步驟如下[10]。

(1)u0(t)=x(t)，j=1；

(2)分別用上述六種方法提取信號uj-1(t)均值曲線：m1(t),m2(t), …,m6(t)；

(3)將上述均值曲線mi(t)從uj-1(t)中分離出，得到剩余信號ri(t)，即

ri(t)=uj-1(t)-mi(t)(i=1, 2, … 6)

(5)

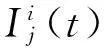
uj(t)=uj-1(t)-Ij(t)

(6)

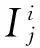
(6)j=j+1，重復上述步驟(2)～(5)，直到剩余分量un(t)為一常函數，或單調函數或能量與u0(t)相比可以忽略的函數，停止上述過程。

原始信號x(t)可重寫為

(7)

GEMD方法綜合了EMD，ITD和LCD等這類分解方法的優勢，繼承了EMD的篩分過程，通過逐層選優，選出GIMF分量，再對剩余信號重復篩分。與EMD等單一的篩分過程相比，GEMD得到的分量在每一層的分量中是最優的，因此，理論上GEMD分解的結果也是最優的。

1.3GIMF判據

GEMD的原文獻采用頻率帶寬最小來選擇GIMF分量。頻率帶寬反映瞬時頻率的調制和波動，頻率帶寬越小，表明瞬時頻率受調制越小，波動越小。

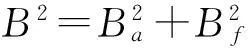
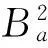
當瞬時頻率為常函數時，帶寬準則能夠很好反映瞬時頻率的聚集性。若φ(t)為非常函數時，帶寬準則失去了預期的結果。此時，采取如下方案來選擇GIMF：

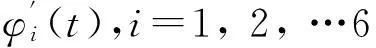
(4)第i個pre-GIMF作為最終的GIMF。

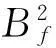
原GIMF判據中通過帶寬準則選擇GIMF，而改進后的判據彌補了帶寬準則的不足，從不同的IMF分量中選擇瞬時頻率更精確，帶寬更小的分量作為最優，相鄰的GIMF分量帶寬無重疊或者重疊更小，因此分解正交性更好。

此外，由于GEMD是從每層不同的IMF分量中選擇最優，如果EMD能將待分解信號分解出，則GEMD也一定能分解出；如果EMD不能分解出，而其它方法定義的均值曲線，如LCM或LIM可以分解出，則說明GEMD也能分解出；只有所有的均值定義方法不能分解出時，GEMD才不能分解出，因此，GEMD的分解能力要比EMD強。

2仿真分析

考慮仿真信號

si(t)=x0(t)+xi(t), i=1,2。 x0(t)=

[1+0.2cos(2π2t)]cos(2πf0t+2πf0/10t2),

x1(t)=cos(2πa1f0t),

x2(t)=cos(2πa2f0t)，t∈[0, 1]

(8)

si(t)由調幅調頻信號x0(t)和余弦信號疊加而成，其中:f0=30,a1=0.5,a2=0.7。為比較，分別采用EMD和GEMD對s1(t)和s2(t)進行分解，分解結果分別如圖1～2和圖4～5所示。

C i表示EMD分解得到的第i個IMF分量， res表示剩余項，下同。 圖1　混合信號s 1(t)的EMD分解結果 Fig.1 The EMD results of mixed signal s 1(t)

G i表示GEMD分解得到的 第i個GIMF分量，res表示剩余項，下同。 圖2　混合信號s 1(t)的GEMD分解結果 Fig.2 The GEMD results of mixed signal s 1(t)

從上到下依次為：第一個和第二個分量與真實分量的絕對誤差(實線表示EMD分解結果的絕對誤差，虛線表示GEMD分解結果的絕對誤差)、EMD分解的重構誤差、GEMD分解的重構誤差。 圖3　混合信號s 1(t)的EMD和 GEMD分解分量的絕對誤差和重構誤差 Fig.3 The absolute error and reconstruction error of mixed signal s 1(t) generated by EMD and GEMD

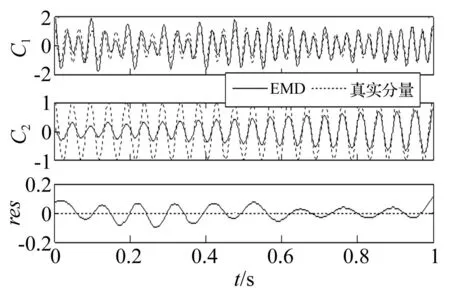
圖4　混合信號s 2(t)的EMD分解結果 Fig.4 The EMD results of mixed signal s 2(t)

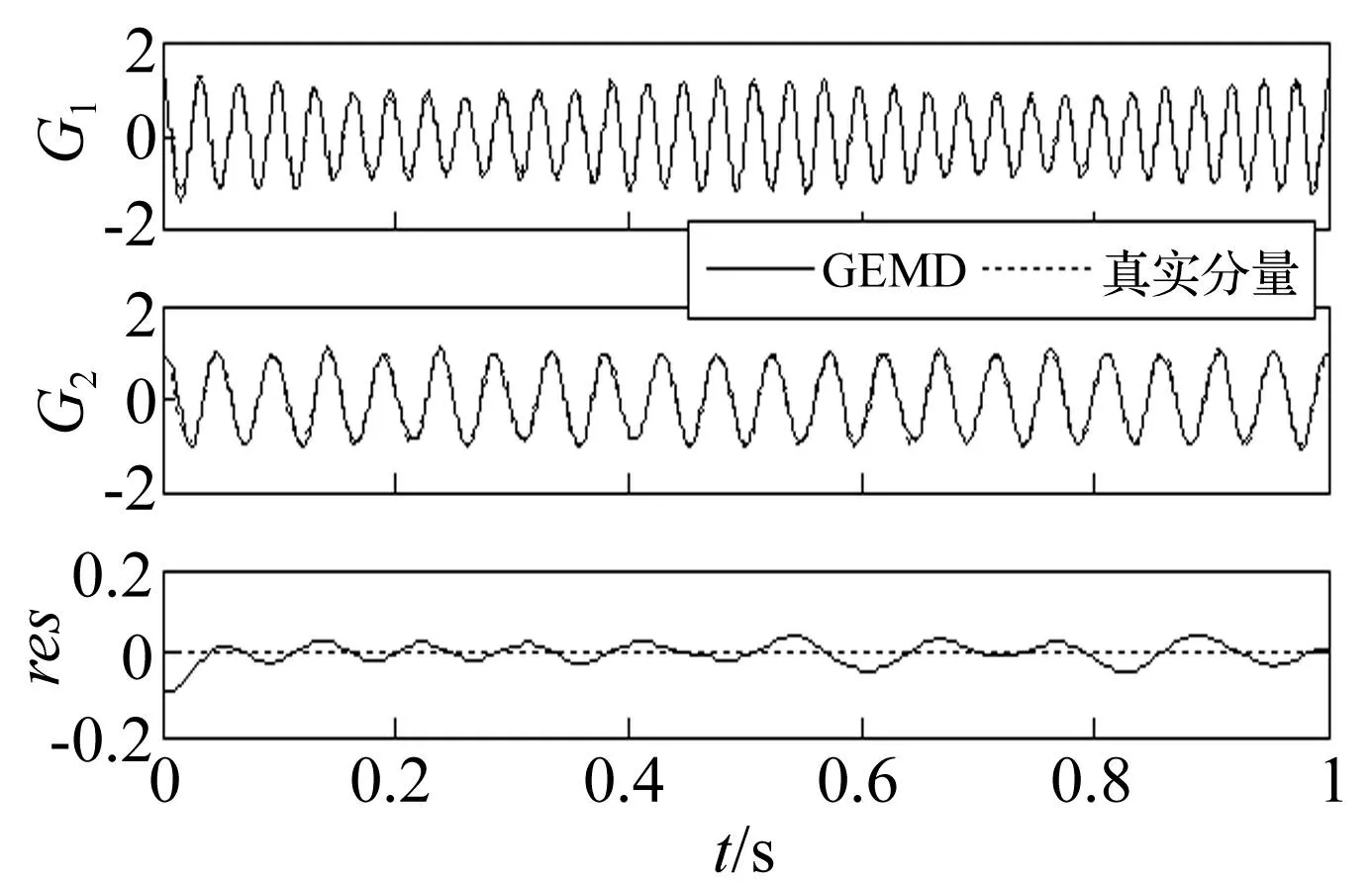
圖5　混合信號s 2(t)的GEMD分解結果 Fig.5. The GEMD results of mixed signal s 2(t)

從上到下依次為：第一個和第二個分量與對應真實分量的絕對誤差，EMD分解的重構誤差，GEMD分解的重構誤差。 圖6　混合信號s 2(t)的EMD 和GEMD分解分量的絕對誤差和重構誤差 Fig.6 The absolute error and reconstruction error of mixed signal s 2(t) generated by EMD and GEMD

分析圖1至圖6可得到以下結論。首先，由圖1和圖2看出，由于兩個分量成分的瞬時頻率(30+6tHz，15 Hz)相差較大，EMD和GEMD都能將二者完全分開，且與真實分量絕對誤差較小(圖3第1, 2行)，但GEMD分解效果更好，GIMF分量與真實分量的絕對誤差幅值在大部分時間上要小于IMF分量與真實分量的絕對誤差幅值。其次，由圖4和圖5可以看出，由于兩個分量成分的瞬時頻率(30+6tHz，21 Hz)較為接近，EMD已不能將二者完全分開，分解結果與真實分量相差較大，而GEMD則能夠將二者完全分開，與真實分量的絕對誤差較小(圖6第1, 2行)。再次，由圖3和圖6也可以看出，對于兩個混合信號，EMD和GEMD分解都是完備的，絕對重構誤差數量級在10-15。

3GEMD分解能力分析

文獻[17]以簡化的兩個正弦信號的疊加模型，對EMD方法的分解能力進行了詳細的研究。為了對比分析，仍考慮兩個正弦信號疊加模型：

x(t)=cos2πt+acos(2πft+φ)

(9)

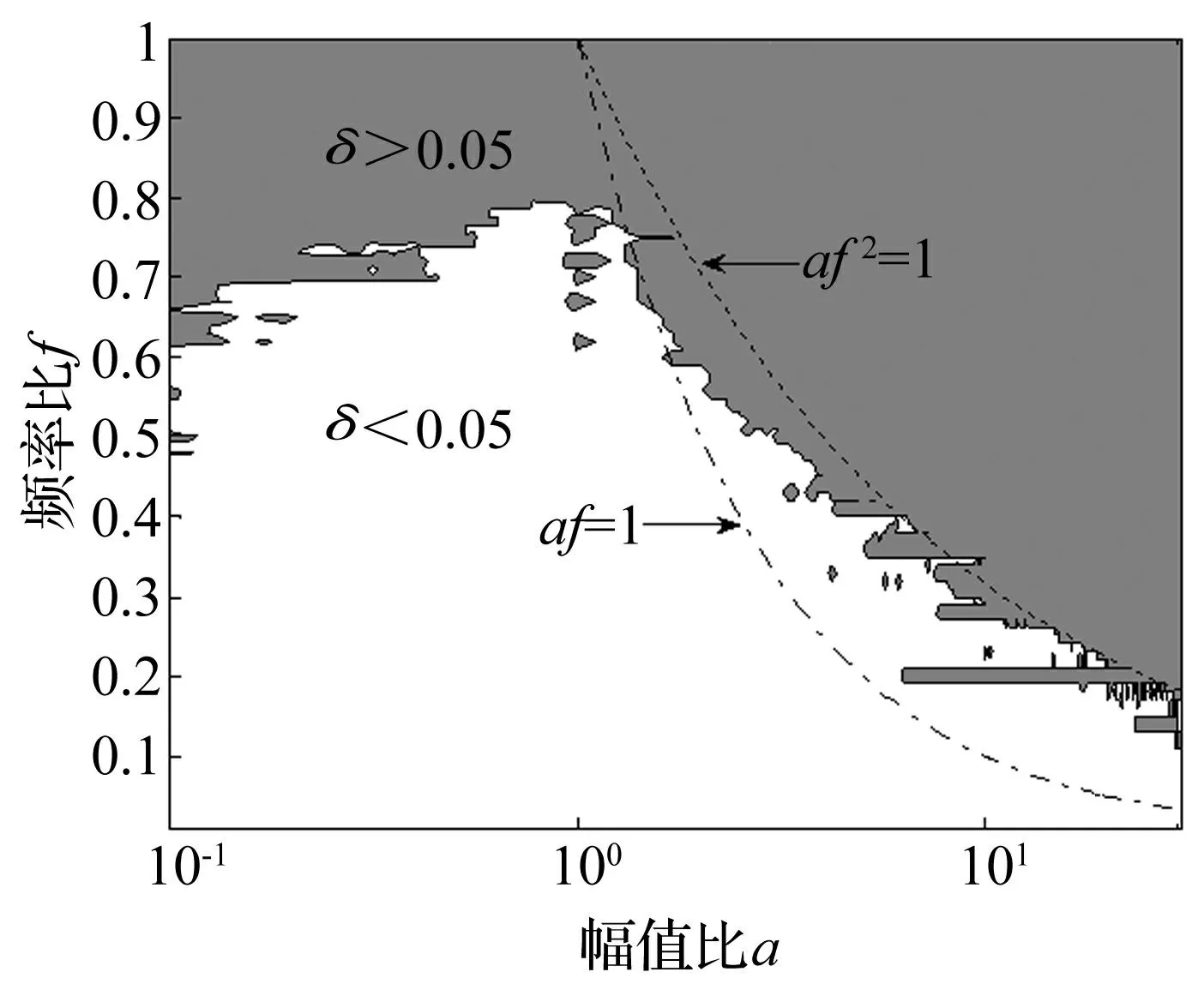
其中:φ表示兩信號的初相位差，a表示兩信號幅值比，f(0

定義評價指標

δ(a,f)=

(10)

圖7　兩個諧波疊加模型的EMD的分解能力圖 Fig.7 The capacity of EMD decomposition of two harmonic superposition model

EMD和GEMD的分解能力分別如圖7和圖8所示。需要說明的是，圖7中EMD可分解的分界頻率(設為fc)與文獻[17]有所差異，這主要是因為采樣頻率fs以及fs與最大頻率fmax的關系對分解效果的影響[19-20]。由圖7和圖8可以發現，在相同的采樣頻率和最大頻率，相同的最大迭代次數(8次)等條件下，GEMD的分解能力范圍要明顯大于EMD的分解能力范圍。在幅值比a≥1時，曲線af2=1可視為不可分解部分的下邊界，af=1可視為可分解部分的上邊界。但在二者曲線之間的部分，GEMD的可分解部分仍大于EMD的可分解部分。此外，在幅值比0.1a1時，GEMD能分別出頻率更接近的信號。更詳細地，①當0.1≤a<0.2時，GEMD可分解邊界頻率fc≈0.6；EMD可分解邊界頻率fc≈0.4；②當0.2≤a<0.6時，GEMD可分解邊界頻率fc≈0.7；而EMD可分解邊界頻率fc≈0.5；③當0.6≤a≤1時，GEMD的可分解邊界頻率fc≈0.77. 而EMD可分解邊界頻率fc≈0.55。

圖8　兩個諧波疊加模型的GEMD的分解能力圖 Fig.8 The capacity of GEMD decomposition of two harmonic superposition model

4應用分析

為了說明GEMD的有效性和相對于EMD的優越性，論文將其應用于具有故障的機械振動信號分析。實驗數據采用美國凱撒西儲大學公開的軸承數據[21]，采用電火花技術對6205-2RS JEM SKF型深溝球軸承設置大小為0.017 78 cm，深度0.027 94 cm的單點故障；在轉速為1 750 r/min,負載為0 HP，采樣頻率為12 kHz的條件下，采集振動加速度信號。不失一般性，以外圈故障軸承的振動加速度信號為例，經計算，轉頻：fr≈29.2 Hz，外圈故障特征頻率：fo≈104.6 Hz。振動信號時域波形如圖9所示。

圖9　具有外圈故障的軸承振動加速度信號 Fig.9 Vibrationacceleration signal of rolling bearing with out race fault

采用GEMD對其進行分解，結果如圖10所示。為了比較和識別故障頻率，圖11畫出了前五個GIMF的包絡譜。由圖11可以看出，前四個高頻分量被故障特征頻率調制，第五個分量被故障特征頻率和轉頻調制，解調后的包絡譜很明顯地反映了外圈故障特征，與實際相符。

其中:G i表示第i個GIMF，圖中只畫出了前五個GIMF及剩余項 圖10　圖9所示信號的GEMD分解結果 Fig.10 The results of signal shown in fig.9 decomposed by GEMD; G istands for the ith GIMF and only the first five GIMFs and its residue are shown.

圖11　從上到下依次為前五個GIMF的包絡譜 Fig.11 Envelope spectrum of the first five GIMFs

其中:c i表示第i個IMF，圖中只畫出了前五個IMF及剩余項 圖12　圖9所示信號的EMD分解結果 Fig.12 The results of signal shown in fig.9 decomposed by EMD; c i stands for the ith IMF and only the first five IMFs and its residue are shown

圖13　從上到下依次為前五個IMF的包絡譜 Fig.13 Envelope spectrum of the first five IMFs

采用EMD對圖9所示的信號進行分解，結果如圖12所示，為了與GEMD結果比較，其前五個分量的包絡譜如圖13所示。由圖中可以看出，前三個IMF的包絡譜與前三個GIMF的包絡譜非常接近，從中也可以識別故障，而第四和第五個IMF的包絡譜包含的信息則不明顯，故障特征頻率和轉頻被低頻干擾較嚴重。因此，比較而言，GEMD分解有一定的優越性。

5結論

對最新提出的廣義經驗模態分解(GEMD)方法的完備性和正交性進行了數值驗證，依據GEMD按照頻率從高頻到低頻的分解特征，提出了一種基于瞬時頻率能量波動差的GIMF分量最優評價準則，并對其分解能力進行了詳細研究。得出如下結論：

(1)GEMD與EMD方法篩分流程相似，分解是完備的和正交的，但GEMD有比EMD更好的正交性。

(2)與EMD相比，GEMD分解能力更強，可分解信號的范圍更廣。

(3)將GEMD應用于機械故障振動信號的分析，結果表明GEMD不僅適合于機械振動信號的分析，而且有比EMD更好的故障診斷效果。

綜上，GEMD是一種有效的信號分解方法。當然，GEMD也有其不足之處，如GIMF分量的評價準則直接決定了分解的效果，而最優GIMF選取準則還有待于進一步研究。相信隨著研究的深入和理論的完善，GEMD將會是一種優秀的非線性和非平穩信號處理方法。

參考文獻

[1]Huang N E, Zheng S, Long S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. Roy. Soc. London, 1998, 454: 903-995.

[2]Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J].Proc. R. Soc. London A, 2004, 460: 1597-1611.

[3]Hou T Y, Yan M P, Wu Z. A variant of the EMD method for multi-scale data, Adv. Adapt. Data Anal.1,2009:483-516.

(下轉第155頁) N E, Zheng S, Long S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. Roy. Soc. London, 1998, 454: 903-995.

[2]Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J].Proc. R. Soc. London A, 2004, 460: 1597-1611.

[3]Hou T Y, Yan M P, Wu Z. A variant of the EMD method for multi-scale data, Adv. Adapt. Data Anal.1,2009:483-516.

[4]Chen Qiu-hui, Huang Norden, Riemenschneider Sherman, et al. A B-spline approach for empirical mode decompositions[J].Advances in Computational Mathematics, 2006, 24: 171-195.

[5]Peel M C, McMahon T A, Pegram G G S. Assessing the performance of rational spline-based empirical mode decomposition using a global annual precipitation dataset[J]. Proc. R. Soc. A, 2009, 465: 1919-1937.

[6]Pegram G G S, Peel M C,McMahon T A. Empirical mode decomposition using rational splines: an application to rainfall time series[J]. Proc. R. Soc. A., 2008, 464:1483-1501.

[7]蓋強. 局域波時頻分析方法的理論研究與應用[D]. 大連:大連理工大學, 2001.

[8]鄒巖崑. 局域波分析的理論方法研究及應用[D]. 大連:大連理工大學, 2004.

[9]程軍圣，鄭近德，楊宇. 一種新的非平穩信號分析方法—局部特征尺度分解法[J].振動工程學報，2012, 25(2): 215-220.

CHENG Jun-sheng, ZHENG Jin-de, YANG Yu.A new nonstationary signal analysis approach-the local characteristic-scale decomposition method[J]. Journal of Vibration Engineering, 2012, 25(2):215-220.

[10]Zheng Jin-de, Cheng Jun-sheng, Yang Yu. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1):136-153.

[11]Frei M G,Osorio I.Intrinsic time-scale decomposition:Time-frequency-energy analysis and real-time filtering of non-stationary signals[J].Proc. Royal Soc. A, 2007, 463:321-342.

[12]Hong Hong, Wang Xin-long, Tao Zhi-yong. Local integral mean-based sifting for empirical mode decomposition[J]. IEEE signal processing letters, 2009, 16(10): 841-844.

[13]Cohen L. Time frequency analysis: theory and applications [M]. Prentice Hall Press, 1995.

[14]Xuan B, Xie Q, Peng S.EMD sifting basedon band width [J]. IEEE Signal Process. Lett, 2007,14(8):537-540.

[15]鄭近德，程軍圣，楊宇. 一種新的估計瞬時頻率的方法—經驗包絡法[J].振動與沖擊，2012, 31 (17): 86-90.

ZHENG Jin-de, YANG Yu, CHENG Jun-sheng,A new instantaneous frequency estimation approach-empirical envelope method[J].Journal of Vibration and Shock, 2012, 31 (17): 86-90.

[16]Huang N E, Wu Z H, Long S R, et al. On the frequency [J]. Advances in Adaptive Data Analysis, 2009, 1(2): 177-229.

[17]Rilling G,Flandrin P. One or two frequencies the empirical mode decomposition answers[J]. IEEE Trans. Signal Process., 2008, 56(1): 85-95.

[18]楊宇，曾鳴，程軍圣.局部特征尺度分解方法及其分解能力研究[J].振動工程學報，2012, 25(5)：602-609.

YANG Yu, ZENG Ming, CHENG Jun-sheng.Research on local characteristic-scale decomposition and its capacities[J].Journal of Vibration Engineering, 2012, 25(5)：602-609.

[19]Rilling G, Flandrin P. On the influence of sampling on the empirical mode decomposition[J]. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2006:444-447.

[20]Rilling G, Flandrin P. Sampling effects on the empirical mode decomposition [J]. Advances in Adaptive Data Analysis,2009, 1(1): 43-59.

[21]Xu H B, Chen G H, An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO[J]. Mechanical Systems and Signal Processing,2013,35:167-175. Qiu-hui, Huang Norden, Riemenschneider Sherman, et al. A B-spline approach for empirical mode decompositions[J].Advances in Computational Mathematics, 2006, 24: 171-195.

[5]Peel M C, McMahon T A, Pegram G G S. Assessing the performance of rational spline-based empirical mode decomposition using a global annual precipitation dataset[J]. Proc. R. Soc. A, 2009, 465: 1919-1937.

[6]Pegram G G S, Peel M C,McMahon T A. Empirical mode decomposition using rational splines: an application to rainfall time series[J]. Proc. R. Soc. A., 2008, 464:1483-1501.

[7]蓋強. 局域波時頻分析方法的理論研究與應用[D]. 大連:大連理工大學, 2001.

[8]鄒巖崑. 局域波分析的理論方法研究及應用[D]. 大連:大連理工大學, 2004.

[9]程軍圣，鄭近德，楊宇. 一種新的非平穩信號分析方法—局部特征尺度分解法[J].振動工程學報，2012, 25(2): 215-220.

CHENG Jun-sheng, ZHENG Jin-de, YANG Yu.A new nonstationary signal analysis approach-the local characteristic-scale decomposition method[J]. Journal of Vibration Engineering, 2012, 25(2):215-220.

[10]Zheng Jin-de, Cheng Jun-sheng, Yang Yu. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1):136-153.

[11]Frei M G,Osorio I.Intrinsic time-scale decomposition:Time-frequency-energy analysis and real-time filtering of non-stationary signals[J].Proc. Royal Soc. A, 2007, 463:321-342.

[12]Hong Hong, Wang Xin-long, Tao Zhi-yong. Local integral mean-based sifting for empirical mode decomposition[J]. IEEE signal processing letters, 2009, 16(10): 841-844.

[13]Cohen L. Time frequency analysis: theory and applications [M]. Prentice Hall Press, 1995.

[14]Xuan B, Xie Q, Peng S.EMD sifting basedon band width [J]. IEEE Signal Process. Lett, 2007,14(8):537-540.

[15]鄭近德，程軍圣，楊宇. 一種新的估計瞬時頻率的方法—經驗包絡法[J].振動與沖擊，2012, 31 (17): 86-90.

ZHENG Jin-de, YANG Yu, CHENG Jun-sheng,A new instantaneous frequency estimation approach-empirical envelope method[J].Journal of Vibration and Shock, 2012, 31 (17): 86-90.

[16]Huang N E, Wu Z H, Long S R, et al. On the frequency [J]. Advances in Adaptive Data Analysis, 2009, 1(2): 177-229.

[17]Rilling G,Flandrin P. One or two frequencies the empirical mode decomposition answers[J]. IEEE Trans. Signal Process., 2008, 56(1): 85-95.

[18]楊宇，曾鳴，程軍圣.局部特征尺度分解方法及其分解能力研究[J].振動工程學報，2012, 25(5)：602-609.

YANG Yu, ZENG Ming, CHENG Jun-sheng.Research on local characteristic-scale decomposition and its capacities[J].Journal of Vibration Engineering, 2012, 25(5)：602-609.

[19]Rilling G, Flandrin P. On the influence of sampling on the empirical mode decomposition[J]. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2006:444-447.

[20]Rilling G, Flandrin P. Sampling effects on the empirical mode decomposition [J]. Advances in Adaptive Data Analysis,2009, 1(1): 43-59.

[21]Xu H B, Chen G H, An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO[J]. Mechanical Systems and Signal Processing,2013,35:167-175.