基于改進的希爾伯特振動分解的機械故障診斷方法研究

第一作者唐貴基男，教授，1962年生

基于改進的希爾伯特振動分解的機械故障診斷方法研究

唐貴基，龐彬

(華北電力大學機械工程系，河北保定071003)

摘要：針對多分量機械故障振動信號的特征提取問題，介紹一種基于希爾伯特振動分解(HVD)的時頻分析方法。該方法首先利用Hilbert變換得到原始振動信號的解析信號，然后通過對解析信號的瞬時頻率低通濾波獲得信號中幅值最大分量的瞬時頻率，同時經同步檢測獲得相應的瞬時幅值和初相位，最后經過迭代運算自適應地檢測出原信號各分量的時頻信息。針對HVD方法的邊界效應問題，提出一種基于相關系數準則的波形匹配邊界延拓法對其進行改進。通過兩組仿真信號分析驗證了HVD方法對多分量非平穩信號的分解能力，同時表明改進的HVD方法能很好地抑制邊界效應。給出轉子系統油膜渦動故障診斷實例，驗證了該方法的工程實用性。

關鍵詞：希爾伯特振動分解；多分量信號；時頻分析；波形匹配延拓；機械故障診斷

收稿日期：2014-01-02修改稿收到日期：2014-02-03

中圖分類號:TH133.3；TH17文獻標志碼：A

A mechanical fault diagnosis method based on improved Hilbert vibration decomposition

TANGGui-ji,PANGBin(School of Mechanical Engineering，North China Electric Power University，Baoding 071003，China)

Abstract:A time-frequency approach based on Hilbert vibration decomposition (HVD) method was introduced in order to extract fault features of multi-component mechanical fault vibration signals accurately. Firstly, the analytical signals of the original vibration signals were obtained through Hilbert transformation. Secondly, the instantaneous stationary frequency of the largest amplitude component was achieved using a low-pass filtering of analytical signals’ instantaneous frequencies, the corresponding amplitude and initial phase were also estimated according to the synchronous detecting, then the time-frequency information of each component of the original signal was detected adaptively with iteration computation. Aiming at the end effects of HVD, a wave matching extending method based on correlation coefficient criteria was proposed to improve HVD. The analysis of two groups of simulated signals showed a good capacity of HVD in decomposing the non-stationary multi-component signals, and the results showed that the improved HVD suppresses its end effects. Finally, a fault diagnosis instance of an oil whirl of a rotor system was given to validate the feasibility of this method.

Key words:Hilbert vibration decomposition; multi-component signal; time-frequency analysis; wave matching extending；mechanical fault diagnosis

機械系統元件發生故障時，振動信號通常為多分量非平穩信號，采用合適的時頻分析方法提取振動信號中各個分量的時頻分布信息是故障特征提取和故障類別判斷的關鍵[1]。機械故障診斷中常用的時頻分析方法有：Wigner-Ville分布、小波分析、希爾伯特黃變換(Hilbert Huang Transform, HHT)等[2-4]。其中：Wigner-Ville分布具有理論上最高的時頻凝聚性，但處理多分量信號時存在嚴重的交叉項干擾問題[5]。小波分析缺乏足夠的自適應性，一旦小波基函數選定，那么所有數據都必須用此小波函數分析，易造成信號的能量泄漏，使定量的時頻分析變得困難[6]。HHT由EMD和希爾伯特變換兩部分組成，方法簡單，應用較廣。但EMD理論上具有模態混疊、端點效應、過包絡、欠包絡等缺陷，很大程度上影響了HHT的分析精度[7]。

希爾伯特振動分解是Feldman等[8]在總結上述時頻分析方法基礎上提出的一種非平穩信號分析的新方法。該方法首先利用Hilbert變換獲得原始信號的解析信號，然后通過低通濾波對原信號的非平穩頻率成分進行分離，獲得信號中幅值最大的分量的瞬時頻率，并經同步檢測得到該分量的瞬時幅值和初相位，最后通過迭代運算自適應檢測出原信號各個分量的時頻信息。HVD和HHT方法都以希爾伯特變換為基礎，但HVD方法避免了HHT方法中復雜的EMD過程，對多分量非平穩信號進行分析，具有分解精度高，分解速度快的優點。針對HVD的邊界效應問題，提出一種基于相關系數準則的波形匹配邊界延拓法來對其進行改進。應用該方法對仿真信號和轉子系統油膜渦動實驗測試信號進行分析，分析結果驗證了HVD方法對非平穩信號良好的時頻分析效果，通過對比分析表明改進后的HVD方法消除了自身的端點問題，使得分析結果更加精確。

1HVD的基本原理

1.1Hilbert變換

任一非平穩連續時間信號x(t)的Hilbert變換可表示為[9]

(1)

(2)

式中：A(t)和φ(t)分別對應x(t)的瞬時幅值和瞬時相位，表達式分別為

(3)

(4)

對應瞬時頻率表達式為

(5)

1.2幅值最大分量的頻率估計

多分量非平穩信號x(t)可表示為[10]

(6)

式中：N為x(t)中的分量個數，al(t)、fl(t)、θl、φl(t)分別表示第l個分量的瞬時幅值、瞬時頻率、初相位和相位。則經Hilbert變換，x(t)的解析信號為

(7)

參考文獻[10]，x(t)的瞬時幅值A(t)可表示為

(8)

其中:

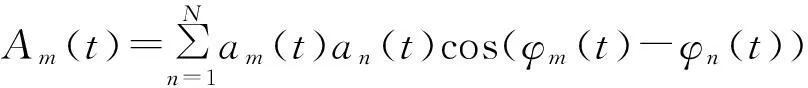
(9)

式中：m=1,2,N

同時x(t)的瞬時頻率f(t)可表示為

(10)

上式表明f(t)可表示為兩部分，其中第1部分f1(t)為幅值最大分量的瞬時頻率，第2部分為相對于f1(t)快速變化的振蕩頻率部分。因而實際應用中可通過低通濾波濾除f(t)的高頻振蕩頻率，得到幅值最大分量的瞬時頻率f1(t)。本文采用FIR低通濾波器，為了實現不同瞬時頻率成分的完全分離，截止頻率fc需小于相鄰次分量瞬時頻率差值絕對值的最小值，則fc越小越能實現不同分量的準確檢測。通常fc設為采樣頻率的0.01～0.05倍時即可完全濾除f(t)的高頻振蕩頻率。實際分析中在考慮濾波器穩定性的前提下，若需要設定更小的截止頻率，可采用降采樣的方法實現。

1.3同步檢測求幅值和相位

將以上估計的瞬時頻率看作參考頻率fr(t)，構造兩正交信號cos(2π∫fr(t)dt)、sin(2π∫fr(t)dt)。將x(t)與cos(2π∫fr(t)dt)相乘得下面表達式

cos(2π∫(fl=r(t)+fr(t))dt+θl=r))

(11)

同理將x(t)與sin(2π∫fr(t)dt)相乘得

sin(2π∫(fl=r(t)+fr(t))dt+θl=r))

(12)

(13)

(14)

從而同步檢測得到瞬時頻率為fr(t)的分量的瞬時幅值ar(t)和初相位θr為：

(15)

(16)

1.4迭代運算

根據上述步驟提取出x(t)中幅值最大的分量

x1(t)=a1(t)cos(2π∫f1(t)dt+θ1)

(17)

將x(t)與x1(t)的差作為初始信號，即

xN-1=x(t)-x1(t)

(18)

重復1.2和1.3節的步驟獲得x2(t)。通過迭代運算依次獲得其他分量的時頻信息，將式(18)的歸一化標準差作為迭代終止條件σ，當σ<0.001時迭代停止。

2基于相關系數準則的波形匹配邊界延拓法

HVD算法以Hilbert變換為基礎，并且在對各分量的頻率、幅值、和相位估計過程中應用到了低通濾波。由于Hilbert變換和低通濾波均存在邊界效應，使得當前分量的檢測產生誤差。并且隨著迭代運算的不斷累積，誤差會越來越大，嚴重影響了HVD算法的檢測精度。目前，解決邊界效應的一種有效方法是對信號進行邊界延拓[11]。為降低數據延拓的偶然性誤差，本文提出一種基于相關系數準則的波形匹配邊界延拓新方法。具體步驟如下：

(1)假設樣本數量為n的離散信號x(t)為{x(t1)，x(t2)，x(t3)，…，x(tn)},共有m個極大值點和p個極小值點，其中信號采樣間隔t=ti-ti-1。極大值點：indmax={M(1)，M(2)，…，M(m)}，對應時間為tmax={tmax1，tmax2，…，tmax m}。極小值點：indmin={N(1)，N(2)，…，N(p)}，對應時間為tmin={tmin1，tmin2，…，tmin p}。

(2)如圖1所示，以左邊界第一極值點為極大值點為例，選取左端點到第2個極值點間的波形{x(t1) ，…，x(tmax1) ，…，x(tmin1)}為研究對象，記為w1。

圖1　波形匹配示意圖 Fig.1 Waveform matching schematic diagram

(3)依次以M(2)，…，M(m)為中心定義與w1同樣長度的子波形wi(i≥2)，wi={x(tmaxi-(tmax1-t1)), …,x(tmaxi), …,x(tmax i+(tmin1-tmax1))}。分別求w1與wi的相關系數值xg作為兩個波形的匹配系數，其中

(19)

式中：E[?]表示數學期望，μw1和μwi分別為波形w1和wi的均值，δw1和σwi分別為原信號w1和wi的標準差。

(4)取xg絕對值最大的子波形wi為w1的最佳匹配波形，將wi前的信號數據延拓到x(t1)左側，延拓點數根據需要選擇。

(5)按照同樣的方式對信號進行右邊界延拓。

(6)對延拓后的信號進行HVD分析，根據原始信號的長度及在原始信號在延拓信號中對應的位置截取分析結果。

3仿真信號分析

仿真信號1：考察一兩分量調頻信號

x1(t)=sin(2π100t+cos(2π5t))+

0.5sin(2π200t+cos(2π40t))

(20)

圖2　x 1(t)的EMD分析結果 Fig.2 EMD analysis results of x 1(t)

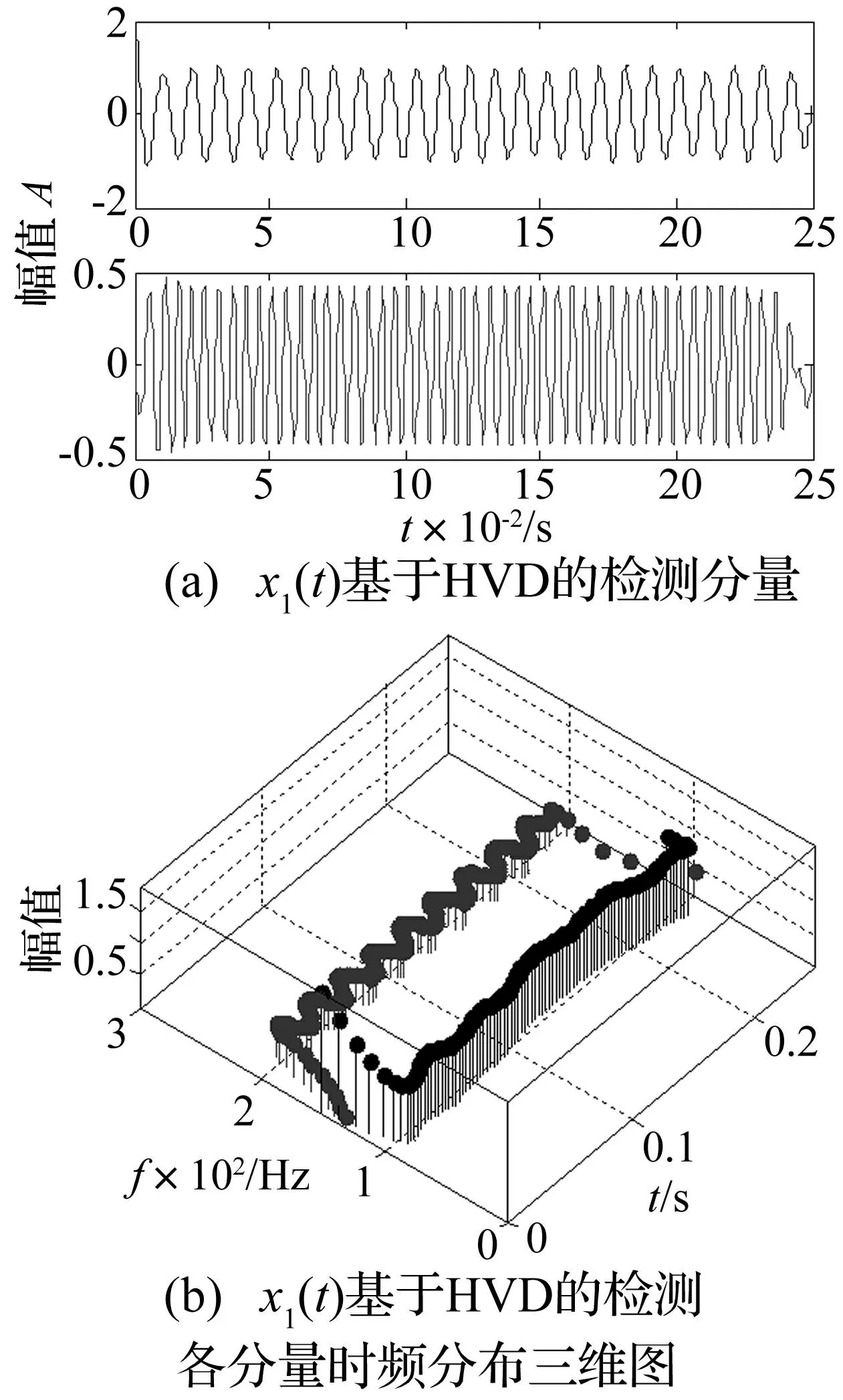
圖3　x 1(t)直接進行HVD分析結果 Fig.3 HVD analysis of x 1(t) without improving

式中：t[0,0.25]，信號采樣頻率fs=4 096 Hz。圖2為信號經EMD分析得到的前兩個IMF分量，兩個分量分別出現了一定程度的模態混疊和幅值失真現象。圖3(a)為x1(t)直接用HVD方法分析得到的兩個分量，圖3(b)為對應的時頻分布三維圖。從分析結果中看出HVD方法克服了EMD方法的模態混疊和幅值失真問題，但存在明顯的邊界效應問題。并且隨著分解過程的繼續，第2個分量的端點效應比第1個分量更為明顯。圖4(a)、圖4(b)分別為本文改進的HVD方法對x1(t)分析得到的分量和時頻分布三維圖，兩個分量的邊界效應得到抑制，使得時頻分析結果更加準確。

仿真信號2：考察一兩分量調幅調頻信號

x2(t)=(2+0.5cos(10πt))sin(300πt+cos(20πt))+

(1+0.4cos(20πt))sin(900πt+cos(40πt))

(21)

分析時間t[0,1]，信號采樣頻率fs=2 048 Hz。圖5、圖6分別為直接用HVD方法和改進HVD方法對x2(t)的分析結果。可見HVD方法有效提取了x2(t)兩個分量的時頻信息，同時經過改進有效克服了HVD方法自身的邊界效應。

仿真信號以兩組多分量調制信號為例驗證了HVD方法對多分量非平穩信號的時頻分析能力。齒輪、軸承、轉子等旋轉機械元件的故障振動信號通常為多分量非平穩信號，HVD方法為此類機械元件的故障特征提取和故障類型判斷提供一種新的途徑。

圖4 x1(t)基于改進的HVD分析結果Fig.4Analysisofx1(t)basedonimprovedHVD圖5 x2(t)直接進行HVD分析結果Fig.5HVDanalysisofx2(t)withoutimproving圖6 x2(t)基于改進的HVD分析結果Fig.6Analysisofx2(t)basedonimprovedHVD

4油膜渦動故障診斷實例

利用Bently RK-4轉子實驗臺模擬了2 800 r/min轉速下轉子系統油膜渦動故障。實驗數據由美國Iotech 公司生產的 ZonicBook/618E信號采集設備采得，采樣頻率為1 280 Hz，采樣點數為1 024。

油膜渦動是轉子軸頸在軸承運動過程由于受到油膜力的作用，轉子繞自身軸心旋轉，同時軸心又繞軸承中心連線回轉的一種運動形式，渦動頻率約為轉速的0.47倍[11]。

圖7　油膜渦動故障信號時域波形 Fig.7 Time domain waveform of oil whirl

圖7為轉子油膜渦動故障信號的時域波形。圖8(a)為油膜渦動故障信號運用改進的HVD方法分解得到的兩個分量，第一個分量對應渦動信號，第二個分量對應基頻信號。圖8(b)為對應的時頻分布三維圖，兩個分量的瞬時頻率分別為23.25 Hz、46.65 Hz，渦動頻率近似為基頻的一半。可見本文方法有效提取了實驗轉子系統油膜渦動的故障特征。圖9為直接HVD方法的分析結果，雖然也提取到了渦動信號和基頻信號兩個分量，體現出油膜渦動的故障特征，但端點效應比較明顯，極大影響了HVD方法的分析精度。為突出本文方法的優點，同時對油膜渦動故障信號進行了EMD分解，結果如圖10所示，產生6個IMF分量。其中IMF1、IMF2分別對應基頻信號和渦動信號。與改進的HVD方法相比，兩個包含故障特征信息的IMF分量均出現了一定程度的模態混疊和幅值失真現象，代表的物理過程被干擾，不能體現設備的真實狀態。對比分析表明改進的HVD方法分解效率高、分解速度快。提取的故障信息更加直觀、準確。

圖8　改進的HVD方法的分析結果 Fig.8 Improved HVD analysis

圖9　直接進行HVD分析結果 Fig.9 HVD analysis without improving

圖10　油膜渦動信號的EMD分析結果 Fig.10 Analysis results of EMD for oil whirl signal

5結論

本文介紹了一種多分量非平穩信號的時頻分析新方法——希爾伯特振動分解(HVD)。該方法以Hilbert變換為基礎，可以自適應地將原始振動信號的各個分量分解出來，通過檢測各個分量的頻率、幅值和相位信息，提取振動信號的故障特征，具有分解精度高、分解速度快的優點。針對HVD方法自身的邊界效應問題，提出一種基于相關系數準則的波形匹配邊界延拓法對HVD方法進行改進。通過仿真信號分析驗證了HVD方法對多分量信號的分解能力和本文方法對HVD邊界效應的改進效果。最后給出轉子系統油膜渦動故障診斷實例，取得很好的分析效果，為機械故障診斷提供一種新的途徑。

參考文獻

[1]程軍圣，楊宇，于德介．基于廣義解調時頻分析的多分量信號分解方法[J]. 振動工程學報, 2006, 19(6)：563-568.

CHENG Jun-sheng, YANG Yu, YU De-jie. A multi-component signal decomposition method based on the generalized demodulation time-frequency analysis [J]. Journal of Vibration Engineering, 2006,19(6)：563-568.

[2]來五星，軒建平，史鐵林，等．Wigner-Ville時頻分布研究及其在齒輪故障診斷中的應用[J]. 振動工程學報, 2003, 16(2)：247-250.

LAI Wu-xing, XUAN Jian-ping, SHI Tie-lin, et al. Research of Wigner-Ville time frequency and application in detecting gear pinion fault[J]. Journal of Vibration Engineering, 2003, 16(2)：247-250.

[3]張曉峰，李功燕．應用小波分析提取故障診斷信號的特定頻段[J]．振動與沖擊，2004, 23(4)：47-50.

ZHANG Xiao-feng, LI Gong-yan. Review on structural control for offshore platforms [J]. Journal of Vibration and Shock, 2004, 23(4)：47-50.

[4]Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. R. Soc. Lond. A, 1998, 454：903-995.

[5]郭琦，劉卜瑜，史立波，等．基于二次 EEMD的Wigner-Ville分布旋轉機械故障信號分析及試驗研究[J]．振動與沖擊，2012, 31(13)：129-133.

GUO Qi, LIU Bo-yu, SHI Li-bo, et al.Experimental study and fault signals analysis of machinery based on dual EEMD and Wigner-Ville distribution [J]. Journal of Vibration and Shock, 2012, 31(13)：129-133.

[6]向玲，唐貴基，胡愛軍．旋轉機械非平穩振動信號的時頻分析比較[J]．振動與沖擊，2010, 29(2)：42-45.

XIANG Ling, TANG Gui-ji, HU Ai-jun.Vibration signal s time-frequency analysis and comparison for a rotating machinery [J]. Journal of Vibration and Shock, 2010,29(2)：42-45.

[7]羅頌榮，程軍圣，楊宇．基于本征時間尺度分解和變量預測模型模式識別的機械故障診斷[J]．振動與沖擊，2013, 32(13)：43-48.

LUO Song-rong, CHENG Jun-sheng, YANG Yu. Machine fault diagnosis method using ITD and variable predictive model-based class discrimination [J]. Journal of Vibration and Shock, 2013, 32(13)：43-48.

[8]Feldman M. Time-varying vibration decomposition and analysis based on the Hilbert transform [J]. Journal of Sound and Vibration, 2006, 295：518-530.

[9]劉慧，劉國海，沈躍．采用希爾伯特振動分解的非整數次諧波檢測新方法[J]．高電壓技術，2009,35(7)：1758-1762.

LIU Hui, LIU Guo-hai, SHEN Yue. Novel method for non integer harmonics measurement using Hilbert vibration decomposition [J]. High Voltage Engineer, 2009, 35(7)：1758-1762.

[10]Feldman M. Theoretical analysis and comparison of the Hilbert transform decomposition methods[J]. Mechanical Systems and Signal Processing, 2008, 22：509-519.

[11]向玲，朱永利，唐貴基．HHT 方法在轉子振動故障診斷中的應用[J]．中國電機工程學報，2007,27(35)：84-88.

XIANG Ling, ZHU Yong-li, TANG Gui-ji. Application of Hilbert-Huang Transform method in vibration faults diagnosis for rotor system [J]. Proceedings of the CSEE, 2007, 27(35)：84-88.