一類三次系統的大同宿分支
尚德生, 周運明, 周愛華
(山東理工大學 理學院, 山東淄博255049)
一類三次系統的大同宿分支
尚德生, 周運明, 周愛華
(山東理工大學 理學院, 山東淄博255049)
摘要:利用多參數攝動理論和微分方程定性理論,通過對一類三次系統擾動形成的大同宿軌研究,得到該系統至少有5個極限環,并給出極限環的分布為3+(1,1)分布.
關鍵詞:攝動; 分支; 三次系統; 極限環; 大同宿軌
1引言與主要結論
文獻[1]研究了下面的 Liénard系統
(1)
證明了對ε的解析函數a1,a2,a3,且|ε|充分小時系統至多存在三個極限環。文獻[2]又研究了系統
(2)
發現系統可以有四個極限環。文獻[3]又進一步討論下面的三次系統
(3)
其中f2(x,y)=a1+a2x+a3x2+a4y2.單純地通過對同宿軌和雙同宿軌的擾動進行研究得到系統(3)可以有五個極限環,其分布為 1+(2, 2)的結構.
首先利用對雙同宿軌擾動得到一個大的同宿軌,然后再研究大同宿軌的穩定性,并利用改變大同宿軌的穩定性的方法進行研究,得到系統(3)仍然可以有5個極限環,但是得到一種新的分布3+(1,1)(即在三個大極限環里面包含兩個分離的小極限環),這種分布是文獻[3]中沒有的. 以定理形式給出.
定理 1 系統 (3)至少可以有5個極限環,其分布是 3+(1,1).
注:利用擾動大同宿軌研究極限環的方法已經在文獻[4]中運用,在這里利用這一方法來討論另外一個不同的多項式系統.
2擾動大同宿軌及引理
由于未擾動系統是Hamilton的,其Hamilton函數為
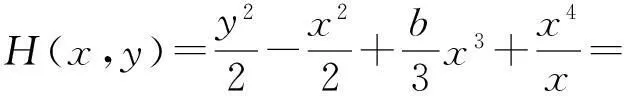
而H(x,y)=0對應未擾動系統的雙同宿軌,記為
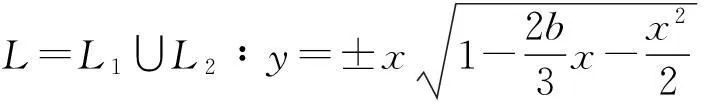
x1≤x≤0,或0≤x≤x2,其中
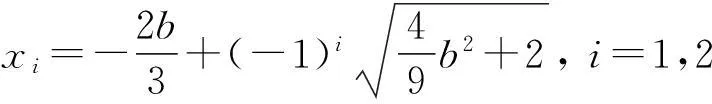

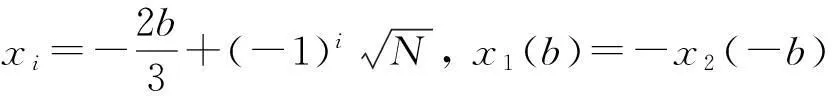
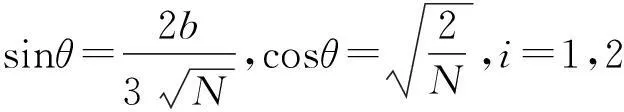
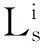
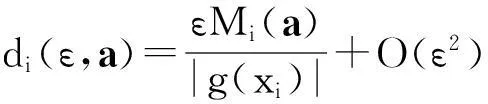
其中
Mi(a)=-∮Li(a1+a2x+a3x2+a4y2)ydx=
2[Ai1a1+Ai2a2+Ai3a3+Ai4a4],i=1,2
(4)
根據文獻[3]的計算得
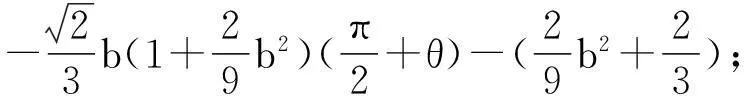
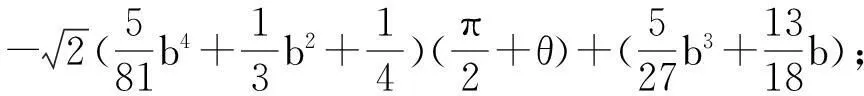
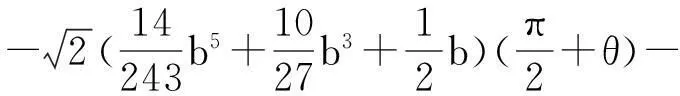
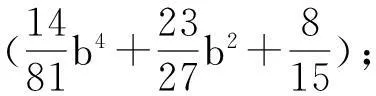
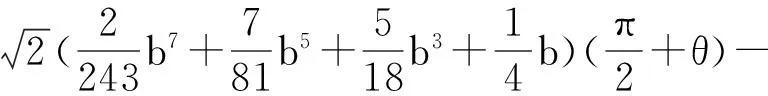
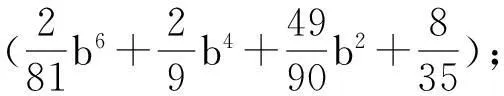
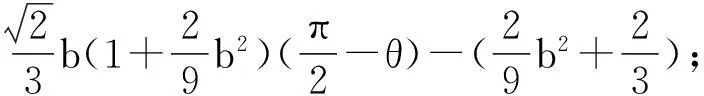
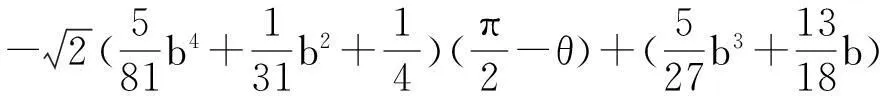
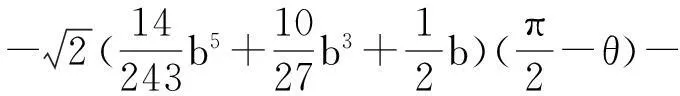
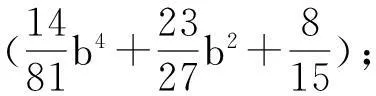
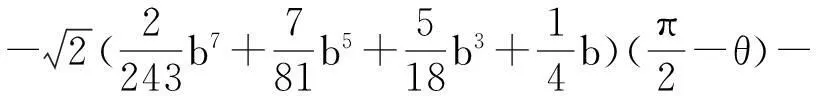
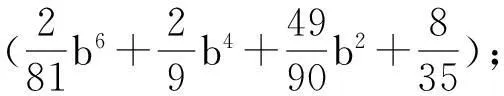
顯然,有下述引理成立
引理 1如果b>0,則存在函數
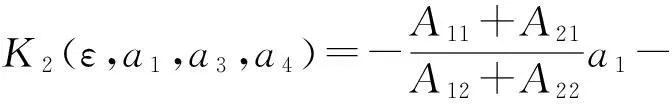
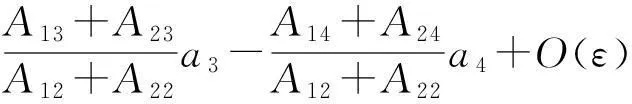
(5)
附近有一個大同宿軌Γ*存在的充分必要條件是
a2=K2(ε,a1,a3,a4),即d1+d2=0
且d1≠0.對于d1>0及d1<0的情況分別見圖1(a)、(b).
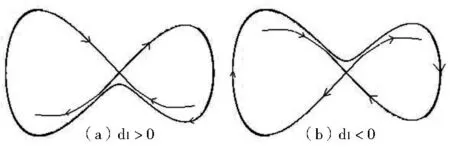
圖1 當d1+d2=0而d1=0時形成的大同宿軌
由于系統(3)在原點擾動下的散度為
div(3)|Oε(0,0)=-εa1+O(ε2),
可得下面的引理成立
引理 2存在函數
K1(ε,a3,a4)=O(ε)
(6)
使得div(3)|Oε(0,0)≥0(<0)當且僅當
a1≤(>)K1(ε,a3,a4).
引理 3 (Ⅰ)如果ai=Ki,i=1,2成立,則當t→±∞時,積分
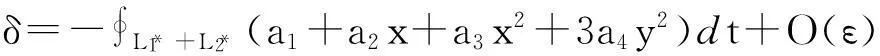
δ=-∮L1+L2(a1+a2x+a3x2+3a4y2)dt+O(ε).
(Ⅱ)當δ>0(<0)時,大同宿軌Γ*是不穩定(穩定)的.
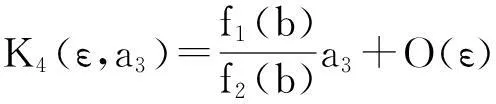
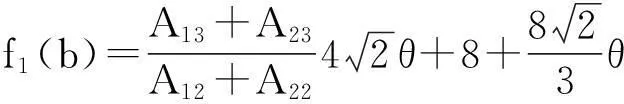
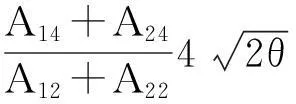
證明 (Ⅰ) (Ⅱ)的證明見文獻[5-6]. 對于(Ⅲ)的證明,結合文獻[2-3]中的計算,得到
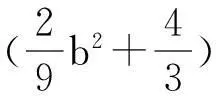
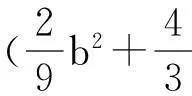
從而在 ai=Ki,i=1,2的條件下有
δ=δ10(b)+δ20(b)=
a3f1(b)+a4f2(b)+O(ε),
其中
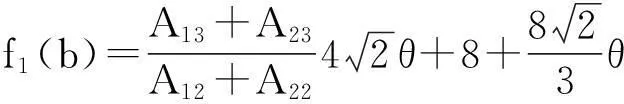
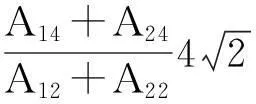
a4≥(<)K4(ε,a3)
(7)
這可以通過化簡并利用Mathematica7.0得到結論(注意:當 b>0時,有f2(b)>0).
根據文獻[6-7]的方法和公式計算在條件 ai=Ki,i=1,2,4下系統關于大同宿軌Γ*的一階鞍點量. 為了便于理解,重述主要結果如下:
對于形如
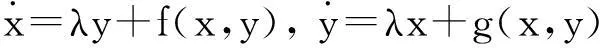
的系統,在原點處的一階鞍點量 R11有下面的計算公式
[fxy(fyy-fxx)+gxy(gyy-gxx)-
fxxgxx+fyygyy]/λ}
這里各函數的導數都是計算其在原點處的值(詳見文獻[7]).
根據該公式易求得系統對應大同宿軌Γ*處的一階鞍點量為
R11=(3a4-ba2-a3)ε.
引理 4在條件ai=Ki,i=1,2,4下,當a3ε>0時,大同宿軌Γ*處的一階鞍點量
R11=-4Ma3ε+O(ε2)<0,
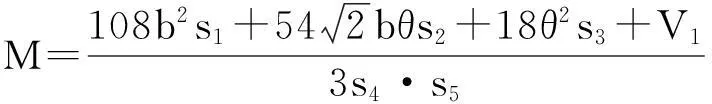
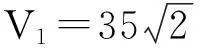
且
s1=529659+379053b2+111510b4+
18060b6+1400b8,
s2=395118+1125819b2+768744b4+
244440b6+40320b8+2800b10,
s3=59049+41553b2+1662606b4+
1524744b6+544320b8+89040b10+5600b12,
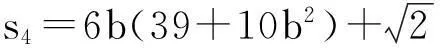
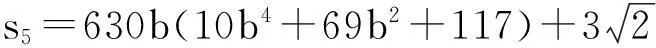
17199b2+7980b4+980b6)θ+140b3(9+2b2)θ2
根據文獻[6]可以得到下面的結果
引理 5 如果大同宿軌Γ*為順時針定向的,且一階鞍點量R11>0(<0),則大同宿軌Γ*為外不穩定 (穩定)的.
3焦點的穩定性
下面討論在條件(5)-(7)下,焦點Piε(xi0+O(ε),O(ε)),i=1,2的穩定性問題,其中
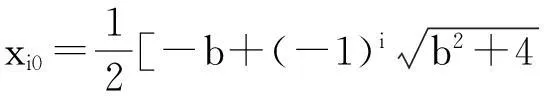
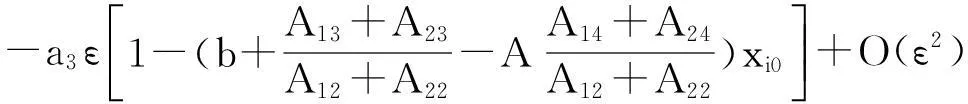
這樣對于奇點Piε,i=1,2處,可以先不考慮前面的-a3ε,利用數學軟件Mathematica7.0分別畫出其在b>0部分的圖像,如圖2所示.
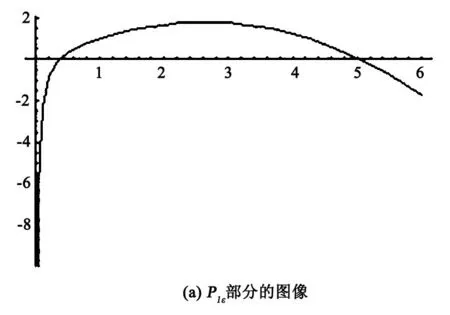
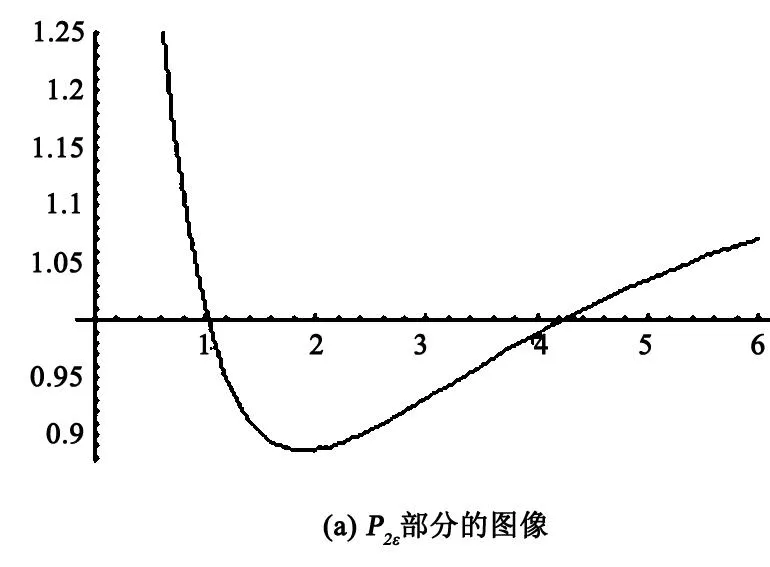
圖2 擾動后焦點Piε的圖像(其中-εa3<0固定)
且可得圖像的兩個零點b1≈0.379626,b2≈5.03778. 這樣根據圖像和-a3ε的符號可得到表1.
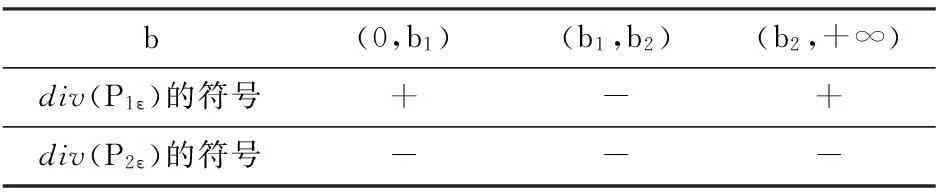
表1 系統(3)在兩焦點Piε,i=1,2處對于
根據文獻[5-6]得到引理6:
引理6當div(Piε)<0(相應地>0)時,焦點div(Piε)是穩定(相應地不穩定的).
4系統的環性分析及定理證明
下面在ε>0充分小且a3>0固定的條件下完成定理1的證明和系統分析.
對于d1+d2=0,且d1>0的情形,根據上述表1及引理6,得到對于b∈(0,b1)的情形,焦點P1ε是不穩定的,而P2ε是穩定的. 這樣根據圖1(b)的大同宿軌內剩余的兩條穩定和不穩定流形走向,可知在大同宿環內各有一個小的極限環出現,它們分別圍繞P1ε和P2ε;對于b∈(b1,b2),由于焦點Piε,i=1,2都是穩定的,故而在大同宿軌內僅有一個小的不穩定極限環出現,它圍繞P2ε;而對于b∈(b2,+∞),情形與 b∈(0,b1)時完全相同,在大同宿軌內也各有一個小環分別圍繞P1ε和 P2ε.
由于R11<0,根據引理5得到大同宿軌是穩定的,這樣對于固定的a3>0,如果|a4-K4| ?a3,且a4>K4,則有δ>0,根據引理4知道大同宿軌這時改變穩定性,即由穩定變成不穩定,可以根據環域定理得到在大同宿軌外有一個穩定的大極限環Γ1,s出現;然后對固定的a3,a4,讓|a1-K1|?|a4-K4|?a3,且a1>K1,這時大同宿軌再次改變穩定性,即由不穩定變成穩定,又可以在大同宿軌外,在Γ1,s內出現一個不穩定的大極限環Γ2,u;最后,對于固定的a1,a3,a4,如果|a2-K2|?|a1-K1|?|a4-K4|?a3,且a2>K2,則大同宿軌破裂,同時原大同宿軌的不穩定流形在穩定流形的外面,從而又有一個穩定的大極限環 Γ3,s出現在Γ2,u內部. 這樣系統(3)在這種情況下會出現3個大極限環套著左右各一個小極限環的現象,記為3+(1,1)(如圖3所示).
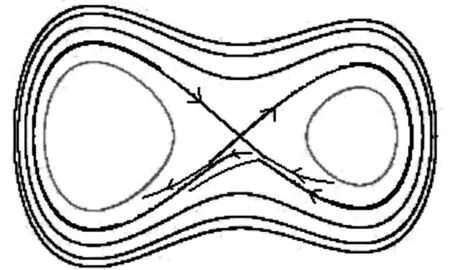
圖3 五個極限環的3+(1,1)分布
其它情形可以類似討論,而出現極限環的個數及分布分別如下:
當d1>0時,若b∈(b1,b2),則為3+(0,1)分布;若b∈(b2,+∞),則為3+(1,1)分布.當d1<0時,若b∈(0,b1),則為3+(0,0)分布;若b∈(b1,b2),則為3+(1,0)分布;若b∈(b2,+∞),則為3+(0,0)分布.
這樣,通過先設定參數使得未擾動系統原先的兩個同宿軌同時破裂并產生一個大同宿軌,然后來研究大同宿軌的穩定性,并通過適當擾動來改變大同宿軌的穩定性,在最后改變參數值讓大同宿軌按照預定的要求破裂的方法,得到系統(3)可以出現5個極限環,其分布為3+(1,1),定理1得證.
注:在該類擾動下系統解的有界性判斷比較困難,所以不能判斷在Γ1,s的外圍是否還有大極限環存在,所以根據我們的方法得到系統(3)可以存在 3+(1,1)分布的至少5個極限環的結論.
參考文獻:
[1]IlieveID,PerkoIM.Higherorderbifurcationsoflimitcycles[J].JournalofDifferentialEquations,1999, 154: 339-363.
[2]韓茂安. 一類三次系統極限環的個數與分布[J]. 數學年刊,2002, 23A(2): 143-152.
[3]ShangDS,HanMA,SunJP.Theglobalbifurcationofacubicsystem[J]. 應用數學學報(英文版), 2006,22(2):325-332.
[4]ShangDS.ThelargeHomoclinic-loopbifurcationofakindofcubicsystem[J]. 數學進展, 2009,38(6): 755-760.
[5]韓茂安,陳健. 雙同宿分支中極限環的個數[J]. 中國科學, 2000, 30A(5): 401-414.
[6]韓茂安. 動力系統的周期解與分支理論[M]. 北京:科學出版社, 2002,287-332.
[7]HanMA,ZhangTH.Somebifurcationmethodsoffindinglimitcycles[J].MathematicalBiosciencesandEngineering(英文版),2006,3(1):67-77.
(編輯:劉寶江)
收稿日期:2014-09-09
作者簡介:尚德生,男,sdsshang@163.com
文章編號:1672-6197(2015)02-0027-05
中圖分類號:O175.12
文獻標志碼:A
The large Homoclinic loop bifurcation of a kind of cubic system
SHANG De-sheng, ZHOU Yun-ming, ZHOU Ai-hua
(School of Science, Shandong University of Technology, Zibo 255049, China)
Abstract:In this paper, the bifurcations of a large homoclinic loop, which obtained by perturbing a kind of cubic system, are considered. Through applying the bifurcation theory of planar dynamical systems, we obtain that the given system can have at least five limit cycles, and the distributions of the limit cycles are 3+(1, 1).
Key words:perturbation; bifurcation; cubic system; limit cycle; large Homoclinic loop

