基于非線性規劃的磁飽和電抗器優化設計

石　翔， 杜欽君， 馬　浩， 徐　帥， 張志見

(1. 山東理工大學 電氣與電子工程學院， 山東 淄博255049;

2. 國網山東煙臺市牟平區供電公司， 山東 煙臺264100)

基于非線性規劃的磁飽和電抗器優化設計

石翔1， 杜欽君1， 馬浩1， 徐帥1， 張志見2

(1. 山東理工大學 電氣與電子工程學院， 山東 淄博255049;

2. 國網山東煙臺市牟平區供電公司， 山東 煙臺264100)

摘要：磁飽和電抗器的設計主要依靠經驗公式和經驗參數，試制出樣機后，根據設計指標與樣機指標的偏差修改設計方案，該方法存在設計精度較低、成本較高的缺點.在磁飽和電抗器設計中，根據約束條件，借助計算機尋優對目標函數求極值，可計算出最適合的設計參數，從而縮短了設計周期，明顯降低了設計及制造成本.

關鍵詞：磁飽和電抗器； 非線性規劃； 優化設計

磁飽和電抗器具有穩定、可靠、穩定運行時間較長等優點，大功率磁飽和電抗器可應用于低壓及高壓交流電動機限流軟起動和動態無功補償[1-6].磁飽和電抗器的設計主要依靠經驗公式和經驗參數，參數選擇隨意性大，備選方案多.試制出樣機后，根據偏差做調整，設計精度較低，成本較高.將優化原則引入磁飽和電抗器設計中，借助計算機尋優，可縮短設計周期，降低成本.

文獻[7]提出了基于量子粒子群算法的電力變壓器優化設計方法，文中提及該方法可適用于其他電氣設備優化設計的求解過程，提高求解過程的收斂速度.文獻[8-9]給出了基于不同算法的空心電抗器的優化設計方法，證明了在空心電抗器設計中應用優化設計方法，可縮短設計周期.但上述文獻都沒有給出與磁飽和電抗器有關的設計方法.文獻[10]提出了一種磁飽和電抗器的簡易設計方法，可運用公式解析法求得電抗器尺寸，但文中提及應用這種設計方法，存在硅鋼片數量和控制繞組銅線的用量較大的問題.文獻[11]論證了在多目標優化設計中可使用線性加權法求得數值解.本文針對現存的磁飽和電抗器優化設計方面的不足，提出基于非線性規劃的磁飽和電抗器設計方法，以硅鋼片、繞組銅線和運行費用作為多目標函數，選擇設計變量作為約束條件，應用線性加權法對優化設計進行求解，以80kVA磁飽和電抗器為例，驗證優化設計的可行性.

1磁飽和電抗器多目標優化設計

1.1 優化設計的數學模型

應用優化算法，計算出一組設計參數，以較高的性價比實現設計指標.

在設計過程中，習慣將設計參數稱為設計變量，為求得優化設計的數值解，將設計目標表示成設計變量x1,x2,…,xn的非線性函數，即f(x1,x2,…,xn)，簡寫為f(x)，f(x)即為目標函數.

在優化設計中必須滿足的設計指標稱為約束.為求得滿足約束條件的數值解，常表示為等式或不等式的形式，如：

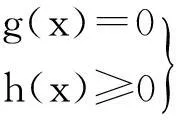
(1)

故優化設計可轉換為存在約束的求解目標函數極小值.數學上稱之為非線性規劃，其一般形式為

(2)

式中：Rn為n維歐氏空間.

1.2多目標優化問題

實際優化問題中，往往要考慮多個設計指標的優化.磁飽和電抗器的優化設計一般需求解相互制約的多個設計指標.如以設計輸出功率為約束，求解功耗最低且質量最小的目標函數.由設計經驗知，電抗器質量M和功耗P是相互制約的，兩者的曲線關系如圖1所示.這時就要折衷處理，選取最佳點.

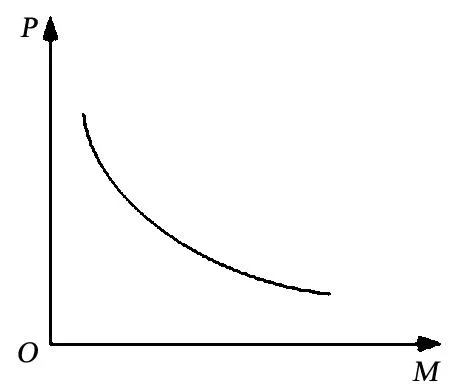
圖1　磁飽和電抗器質量與功耗關系曲線

但多目標函數的求解時間較長，因此，對于多目標優化的工程設計問題，一般轉化為單目標函數，完成極小值計算.常用轉換方法如下：

(1)最小線性加權和.采用將多個目標函數fi(x)(i=1,2,…,m)加權求和的方法將多目標函數轉換為

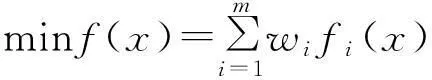
(3)

式中，wi為對fi(x)的加權因子.

(2)平方加權和的開方最小.應用此方法，可將多目標函數轉換為

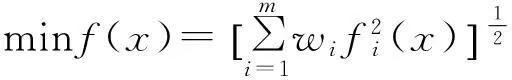
(4)

(3)極小極大法(Minimax Optimization).對多個目標函數求取極大者后，再求取該極大函數的極小值，可將多目標函數可轉換為

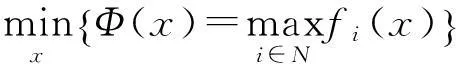
(5)

2設計指標及約束條件

2.1磁飽和電抗器的設計指標

已知三相磁飽和電抗器由三個單相磁飽和電抗器組成.鐵心為矩形，單相鐵心結構如圖2所示.

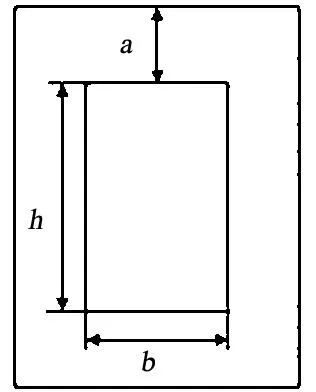
圖2　可變電抗器等效電路圖

本設計給定的設計指標如下：

(1)三相電源線電壓為380V，頻率為50Hz.

(2)磁飽和電抗器三相額定輸出功率為80kVA，負載為純電阻.

(3)工作繞組額定電流為141A.

(4)控制繞組功率為750W，最大控制繞組電流為11A.

(5)繞組溫升不大于80°C.

2.2磁飽和電抗器的基本約束條件

三相磁飽和電抗器的基本約束條件為：

(1)容量約束. 為保證輸出功率大于負載功率，磁飽和電抗器設計容量應大于80kVA.

設電壓、電流波形為正弦，則

(6)

式中：U為電源相電壓有效值；Ug及Ig分別為工作繞組上的壓降和電流，R為負載等效電阻.

當鐵心完全飽和時，可認為Ug=0，這時流過工作繞組的電流為

Igm=U/R

(7)

傳統的磁飽和電抗器設計方法是以UIgm作為磁飽和電抗器容量，實際上，磁飽和電抗器任何工作狀態通過的功率都遠小于UIgm.根據設計要求，磁飽和電抗器設計容量表示為

P(x)=3UIg=3×4.44fBmScj2Sg

(8)

式中：f為電源頻率，取50Hz；Bm為磁飽和電抗器的磁感應強度最大值；j2為工作繞組電流密度；Sg為工作繞組的銅線截面積；Sc為鐵心截面積.

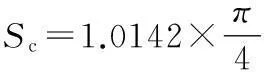
(9)

因而，可得到約束不等式為

P(x)-80000≥0

(10)

(2)鐵心最大磁感應強度約束. 鐵心磁密上下限約束，令在1.6～1.7T之間取值，則

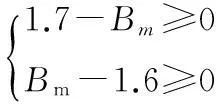
(11)

(3)控制繞組電源容量約束. 通過最大控制繞組電流時，限制控制繞組電阻，以保證控制繞組功率不超過控制電源所能提供的容量；本設計的控制繞組熱功率為750W.

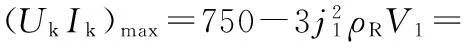
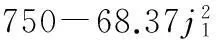
(12)

式中：ρR為銅導線電阻率(設定控制繞組工作溫度100℃，取22.79)；j1為控制繞組電流密度；V1為控制繞組銅線體積.

(4)溫升約束. 大多數電抗器采用B級絕緣材料，一般要求最高溫升不能超過80℃，因此，設計磁飽和電抗器繞組溫升必須低于溫升限值.

由溫升計算公式

80-0.34g0.8≥0

(13)

式中：g為繞組表面熱負荷.

g=(PCu/Sh)×100

(14)

(15)

Sh=3×(Sh1+0.26Sh2)

(16)

(17)

Sh2=(h-0.3)(12.5664d+1.69026)

(18)

式中：PCu為繞組溫度為100°C時銅損；V2為工作繞組銅體積；Sh為有效散熱面積；Sh1為控制繞組散熱面積；Sh2為工作繞組散熱面積.

2.3磁飽和電抗器的附加約束條件

附加約束條件是為了使電抗器具有某方面的性能而在設計時人為設定的等式約束條件.不同的附加約束條件對應著不同的設計方法.

本文采用鐵心結構作為附加設計變量.即矩形鐵心窗口高h；窗口寬b；鐵軛寬a；鐵心柱內接圓直徑d；控制繞組及工作繞組電流密度j1及j2(A/mm2).

根據設計經驗參數可設定如下約束：

鐵心幾何尺寸非負約束

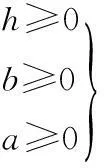
(19)

鐵心柱內接圓直徑上下限約束

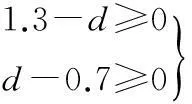
(20)

繞組電流密度下限約束

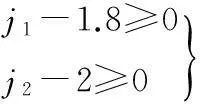
(21)

3磁飽和電抗器的優化模型

目標函數.優化目標是主要材料費及運行損耗費之和為最小.用數學形式表示為

minf(x)=C1(x)+C2(x)

(22)

式中：C1(x)為硅鋼片與繞組銅線費用之和；C2(x)為鐵損與銅損有關的運行費用.C1(x)可表示為

C1(x)=5500MFe+53000MCu

(23)

式中：MFe、MCu分別為三相鐵心質量和三相繞組銅線質量，本設計選用寶鋼B50A470，價格為5.5元/kg，銅線采用芯標稱直徑為1.06mm的漆包線，價格為53元/kg.

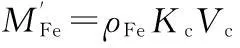
(24)

式中：ρFe為冷軋單取向硅鋼片的密度，取值為7.65×103kg/m3；Kc為疊片系數，取值為0.95；Vc為一相鐵心體積.

一相鐵心毛體積Vc可表示為

Vc=2Sch+2adb+4ad2

(25)

硅鋼片總重(三相)

MFe=3ρFeKcVc=

21.8025×(1.5931h+2adb+4ad2)

(26)

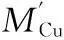
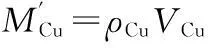
(27)

式中：ρCu=8.89×103kg/m3；VCu為繞組銅線體積.

單相繞組銅線體積為

VCu=V1+V2

(28)

三相繞組銅線質量為

MCu=3ρCuVCu

(29)

計算運行費用時，設磁飽和電抗器可連續工作15年，每年運行360d，日工作16h，工業電費取平均值為0.9元/kWh.

C2(x)=15×360×16×0.9(PCu+PFe)=

77.76(PCu+PFe)

(30)

鐵損為

PFe=PcMFe=3ρFeKcVcpc=

31.613625Vc

(31)

式中：pc為比鐵損，取經驗參數1.45.

將式(15)、式(31)代人式(30)可得C2(x).

最終得約束條件下的目標函數的顯示表達式為

(32)

4磁飽和電抗器優化設計實例

選取三個單相磁飽和電抗器組成的三相磁飽和電抗器為例，設計額定容量為80kvar、額定電壓為380V.采用本文提出的優化模型，借助計算機尋優求解，對電抗器進行了優化設計.優化設計結果與原設計比較見表1.

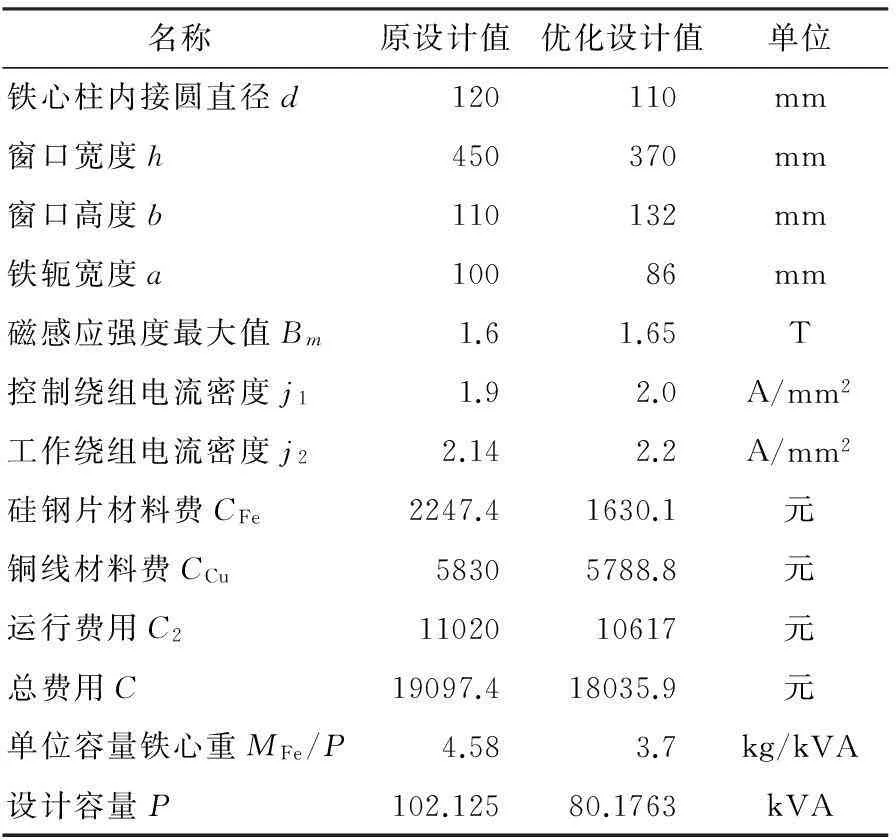
表1　優化設計結果與原設計數值比較

由表1可知：通過該方法優化可以將鐵心柱內接圓直徑d由120mm縮減至110mm，矩形鐵心窗口高h由450mm降低至370mm；鐵軛寬a由100mm縮減至86mm；與原設計比較，優化設計結果使電抗器的Bm、j1、j2略有增大，獲得了較好的性能指標，同時，減少了鐵心質量和銅線質量，節省了材料費用。其中，鐵材料費減少617.3元，銅材料費減小41.2元，運行費用減少403元.單位容量鐵重由4.58kg/kVA下降至3.7kg/kVA，材料利用更合理.

各項費用優化以后下降的百分比(以原設計值為準進行比較)見表2.

表2　優化后費用下降百分比　%

應用Ansoft Maxwell有限元分析軟件建立單相電抗器3D模型，設定電抗器材料屬性為電工硅鋼片，選擇DW315_50作為電抗器鐵心材料，如圖3所示.

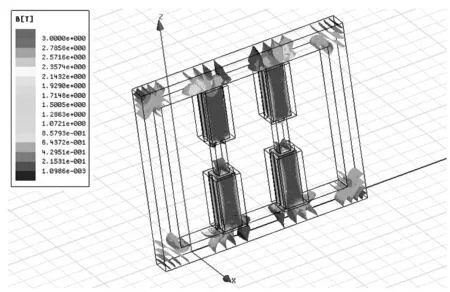
圖3　磁飽和電抗器磁通密度圖

由圖3可知，優化后的電抗器鐵心磁通密度平均在1.5T，局部最高超過3T，理論上已超過DW315_50硅鋼片推薦磁感應強度值(1.8～2T)，早已進入磁飽和狀態，能夠實現調整電抗值的功能.

5 結束語

以磁飽和電抗器的材料費用和運行費用最小作為目標函數，將非線性規劃方法引入到磁飽和電抗器的設計中，建立了矩形鐵心的磁飽和電抗器優化設計模型。 磁飽和電抗器優化模型是非線性規劃問題，包括七個設計變量. 選取設計容量、磁感應強度、控制容量、溫升約束作為基本約束條件；選取鐵心幾何尺寸和繞組電流密度作為附加約束條件，綜合分析了四個基本約束條件的影響，給出了非線性規劃的顯式表達式.設計結果表明，在約束條件的限定下，優化后電抗器的各項性能指標均可滿足設計要求，實現了材料費用和運行費用的多目標優化。優化設計結果中：硅鋼片優化后下降幅度為27.5%，效果明顯；由于導線電流密度限制，銅線體積優化后下降幅度只有0.6%，而其在目標函數占比過大，總費用下降約5.6%.采用本文構建的目標函數，對鐵心質量較大的電抗器進行優化設計，優化結果費用降低明顯。

參考文獻:

[1]黃曉勝, 史歡, 田翠華, 等. 基于磁控電抗器的變電站無功電壓控制[J]. 電力自動化設備, 2011, 31(8): 99-102.

[2]王寶安, 金麗莉, 羅亞橋, 等. 基于磁控電抗器的動態無功補償裝置[J]. 電力自動化設備, 2010, 30(4):97-100.

[3]陳博. 基于PLC的高壓大電機磁控軟啟動裝置[J]. 武漢大學學報:工學版, 2012, 45(2): 220-224.

[4]畢秀梅, 馬英慶. 一種新型靜止無功補償裝置[J]. 電力自動化設備, 2009, 29(8):97-100.

[5]陳鋒, 趙彥珍, 馬西奎. 基于QPSO算法的電力變壓器優化設計[J]. 中國電機工程學報, 2009, 29(21): 99-106.

[6]潘再平, 張震, 潘曉弘. 基于QPSO算法的電力變壓器優化設計[J]. 電工技術學報, 2013, 28(11): 42-47.

[7]張成芬, 趙彥珍, 鄒建龍, 等. 多樣性引導的改進量子粒子群優化算法及其在干式空心電抗器優化設計中的應用[J]. 中國電機工程學報, 2012, 32(18): 108-114.

[8]趙彥珍,康博,馬西奎. 基于附加約束條件平衡原則的干式空心電抗器優化模型[J]. 電工技術學報, 2010, 25(11): 80-84.

[9]張成芬, 趙彥珍, 陳鋒. 等. 基于改進NSGA-Ⅱ算法的干式空心電抗器多目標優化設計[J]. 中國電機工程學報, 2010, 30(18): 110-121.

[10]王玲. 一種簡易飽和電抗器的設計方法[J]. 制造業自動化, 2010, 33(1):31-33.

[11]孫曉輝, 丁曉紅. 結構多目標拓撲優化設計[J]. 機械設計與研究, 2012, 28(4):1-4.

(編輯：劉寶江)

收稿日期：2014-10-19

作者簡介：石翔, 男, 116629689@qq.com； 通信作者： 杜欽君，男，duqinjun@sdut.edu.cn

文章編號：1672-6197(2015)02-0066-05

中圖分類號：TM476

文獻標志碼：A

Optimizationdesignofmagneticallysaturationreactor
basedonnonlinearprogramming

SHIXiang1,DUQin-jun1,MAHao1,XUShuai1,ZHANGZhi-jian2

(1.SchoolofElectricalandElectronicEngineering,ShandongUniversityofTechnology,Zibo255049,China;

2.StateGridShandongYantaiCityMupingDistrictPowerSupplyCorporation,Yantai264100,China)

Abstract:The design of magnetically saturation reactor mainly relies on the experience formula and parameters, while parameters are chosen arbitrarily and randamly. After the prototype trial is developed, according to deviation between the predesigned index and the developed one, design adjustment is made, leading to low precision and high cost. During the magnetically saturation reactor design, the extremum of the objective function is calculated with the constraint condition by computer optimization, and the most suitable design parameters are gained, which shortens design cycle and reduces design cost. By the costs comparison, the manufacturing cost can be significantly reduced and the feasibility of design is improved by nonlinear programming.

Key words:magnetically saturation reactor; nonlinear programming; optimization design