高速自旋目標ISAR成像的代數重構方法?

(北京跟蹤與通信技術研究所,北京100094)

0 引言

逆合成孔徑成像雷達(ISAR)成像是雷達目標識別的主要手段之一,通過這項技術獲得的高分辨圖像是判斷目標結構的重要依據。但真實的空間目標在運動中常常存在自旋等微動現象,這種現象會對雷達回波產生多普勒頻率展寬和距離單元徙動等調制作用。因此,距離多普勒算法(RD)和距離瞬時多普勒算法(RID)等常規ISAR成像方法不僅不能實現對目標的聚焦成像,同時還會在圖像中產生沿方位向的微多普勒干擾帶,掩蓋了圖像中的其他信息。許多情況下,為保證成像質量而采用的分離微多普勒信號的做法會導致小尺寸微動目標重要信息的丟失。因此,如何有效地處理雷達回波中的微動信息,是雷達成像技術應用在空間目標探測中亟需解決的一個難題。

微動是指目標或目標上的獨立結構存在的振動、自旋、進動等物理現象[1-2],這種現象對平動的多普勒頻率產生的調制作用稱之為微多普勒效應。通常,微多普勒效應會對雷達回波信號的分析造成干擾。但是另一方面,目標的微動信息又能成為目標識別和分類的重要依據,因此,近年來針對微動目標的雷達信號處理技術受到了極大關注。美國海軍實驗室的Chen首先系統地提出了微動的概念并詳細分析了由微動造成的雷達回波中的微多普勒效應[3];其后Suresh和Thayaparan等人提出了基于時頻分析技術的微動周期的估計方法[4];針對微動現象對ISAR成像造成的不良影響,國防科技大學的劉進等人提出用Hough變換的方法去除微多普勒效應以提高成像質量[5];2011年,西安電子科技大學的白雪茹等提出了針對自旋目標成像的實數逆Radon變換法(RIRT)和復數逆Radon變換法(CIRT)[6],并應用于實測數據得到了AN-26運輸機的螺旋槳圖。

逆Radon變換原是醫學CT成像中的一類方法[7],運算速度快,但是對數據完備性和信噪比要求較高。代數重構方法是CT成像中的另一類方法,具有抗稀疏性和抗噪性強的優點[8]。本文中根據寬帶雷達回波在距離慢時間域上的表達式和微動中的自旋模型,將代數重構算法推廣到ISAR成像領域,提出了廣義代數重構算法(Generalized Algebraic Reconstruction Technique,GART)。GART主要包括建立線性方程組和迭代求解兩個步驟。針對不同的應用場景,根據是否考慮回波相位信息又可以分為實數GART和復數GART兩種形式。GART具有對模型參數敏感的特點,結合時頻分析技術可以用來對自旋周期進行精確估計。本文用仿真和實測數據驗證了GART的性能,獲得了用常規ISAR成像方法無法得到的目標精細結構,并且提高了目標自旋周期的估計精度。

1 信號模型

在ISAR雷達成像中,微動現象對雷達脈沖回波的調制作用在距離慢時間域上表現為兩個方面:距離向上距離單元的徙動和方位向上多普勒頻率的展寬。為了建立關于目標圖像的線性方程組,首先要對這些調制作用進行詳細分析。

設寬帶雷達發射線性調頻體制(LFM)的信號,表達式如下:

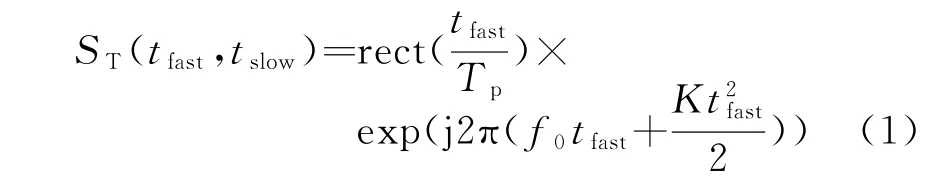
式中,Tp表示脈沖寬度,f0表示中心頻率,K表示調頻率。

圖1所示是自旋目標和雷達的位置關系示意圖,圖中點O是目標的旋轉中心,旋轉的角速度為w,點A是目標上的一個旋轉半徑為r0的散射點,且r0遠小于目標到雷達的距離R0。

圖1 自旋目標示意圖

按照文獻[8]中的推導步驟,自旋目標的雷達回波經過去調頻接收和脈沖壓縮后,信號在距離慢時間域上的表達式為

式(2)所表示的即為高分辨距離像(HRRP)序列,對于每一個慢時間的HRRP,它的實包絡為sinc函數,且對應的極大值點位于:

因此,散射點A對應的距離像上的點隨慢時間在各個距離單元之間移動。

在方位向上,點A的多普勒相位表現為一個隨時間變化的函數:

式(4)即為文獻[3]中提到的微多普勒效應,它導致了多普勒頻率的展寬,從而造成圖像中的散焦現象。

2 廣義代數重構算法(GART)

代數重構算法是醫學CT成像中的一種經典算法,其主要思想是利用X射線從不同角度穿過物體后的衰減率建立方程組,從而求解出物體中各點的透射率。但是在雷達領域,無線電波衰減率的穩定程度不足以用于建立方程,因此,本文中以高分辨距離像代替衰減率作為方程的常數項。

如圖2(a)所示,圖像矩陣表示為Psquare(N×N),設旋轉中心位于Psquare(N×N)的中心,按照圖2(b)所示,將Psquare(N×N)拉直為一個向量:

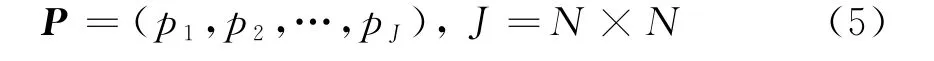
假設散射點A在Psquare上的坐標為(m,n),根據式(3)可知,經過tm時間的旋轉,A點在距離像上對應的極值點位于如果距離向在快時間上的采樣點數為M,則點A對應的距離單元序號為

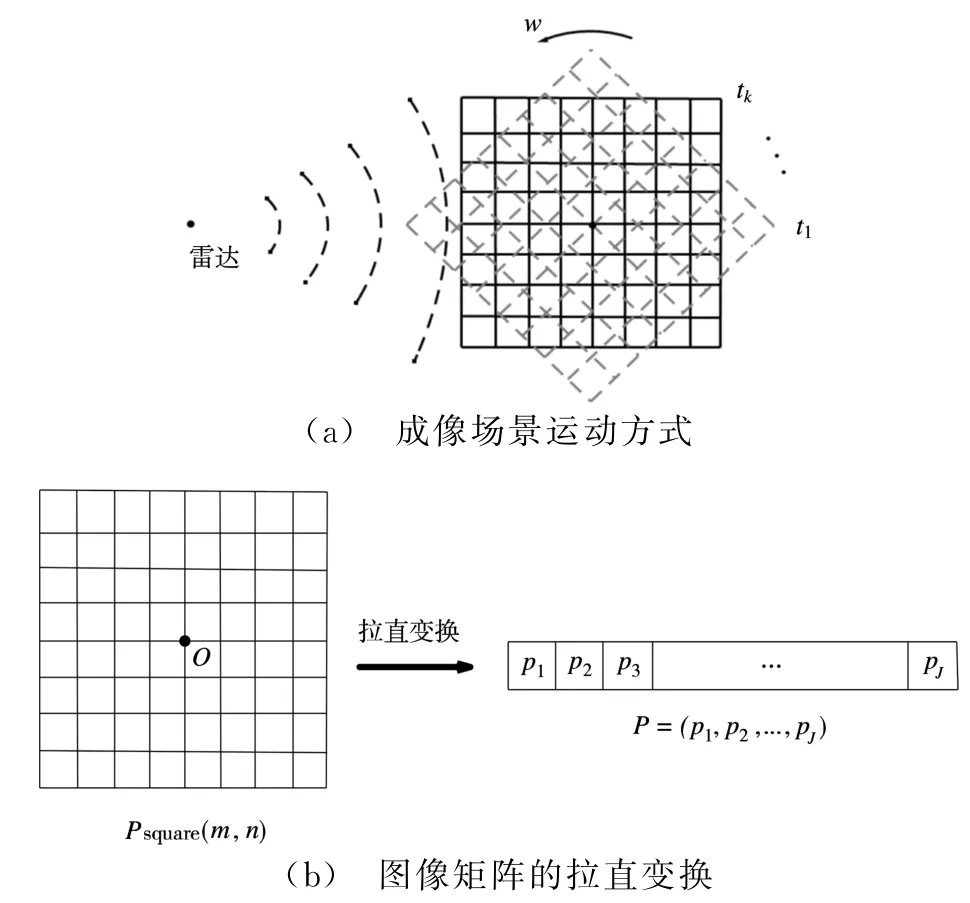
圖2 GART算法原理示意圖

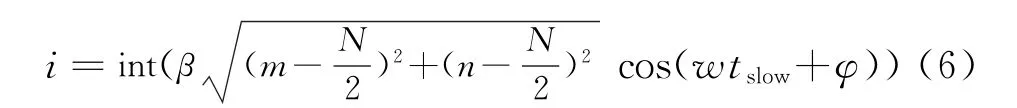
式(3)和式(4)分別代表了回波在慢時間距離域上所包含的實包絡和相位兩部分信息,根據是否考慮相位信息,本文中將GART算法分為實數GART和復數GART。

2.1 實數廣義代數重構算法

在不考慮相位的情況下,采用如下的方式對M行N2列的系數矩陣W(tslow)賦值。

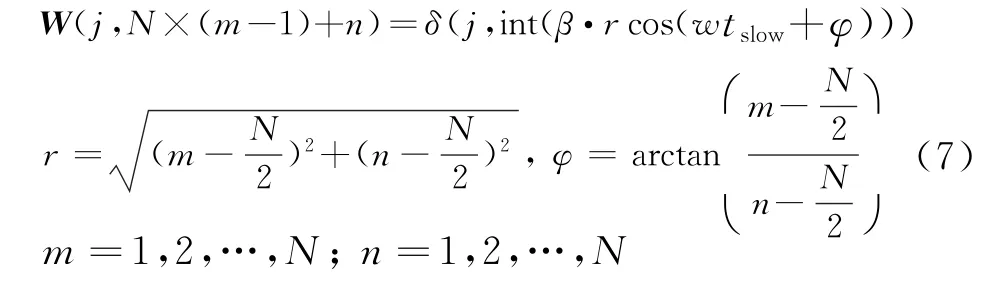
式中,δ為狄拉克函數:

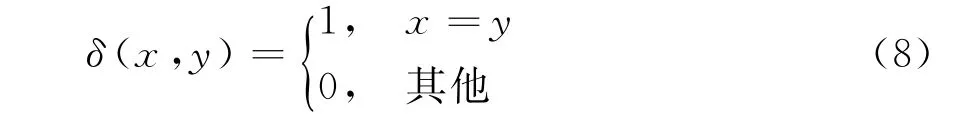
從而,在距離慢時間域上建立了線性方程組:

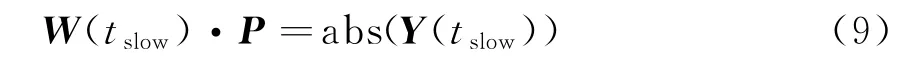
式中,Y(tslow)表示tslow時刻的距離像,由于慢時間tslow取離散值t1,t2,…,t k,…,因此W(t k)和Y(t k)可以用W k和Y k表示。

求解圖像向量P的方式有很多種,大量的有關CT成像的文獻對ART方法的求解進行了深入研究,其目的是提高圖像重構的質量和速度[8]。本文給出一種基于Kaczmarz迭代格式的序貫模塊迭代求解方法(Sequential Modular Iterative,SMI)。

設P k-1是t k-1時刻得到的圖像向量,它在距離慢時間域上的殘差可以表示為

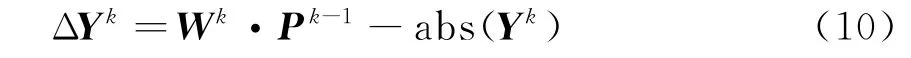
通過W k的廣義逆(W k)-1將該殘差投影到圖像域上:

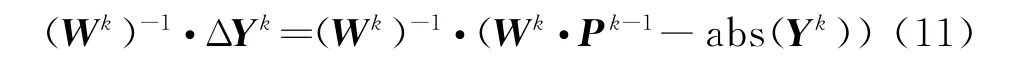
最終得到序貫模塊迭代格式:

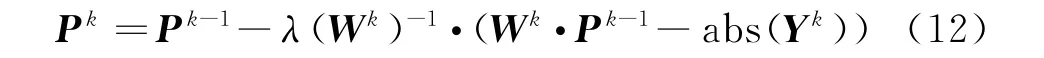
式中,λ為松弛因子,用于控制收斂速度。

2.2 復數廣義代數重構算法

實數GART方法只利用了回波在距離慢時間域上的模值部分,它的相位中同樣包含自旋目標的結構信息,如果加以利用,理論上就能提高圖像的質量。因此,本文對實數GART算法加以修改,得到復數GART。

首先去掉式(9)中的絕對值,保留方程中的線性項的相位信息,同時需要對系數W ip進行如下修正:

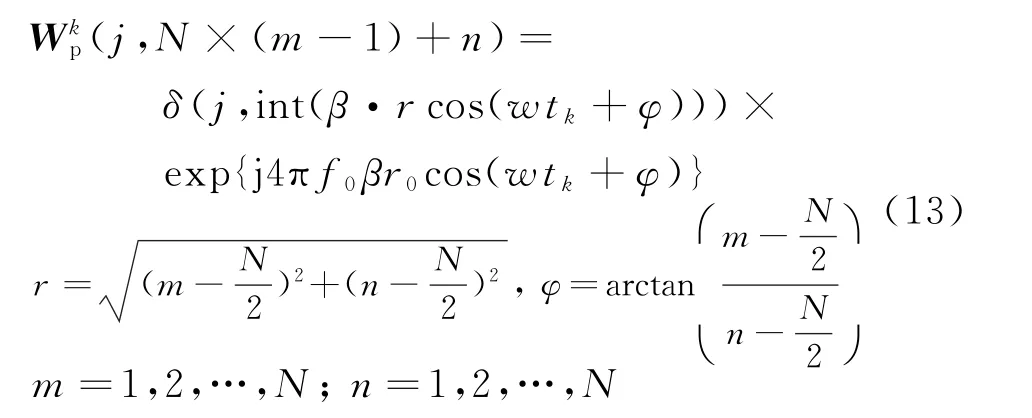
最終得到方程:

通過上述改進,Y k中散射點A對應的相位就會與系數矩陣W kp中的相位相互抵消,從而實現對點A的等相位積累;同時,雜波的相位因為不符合上述模型,故不能實現相干積累。因此,復數GART具有比實數GART更高的分辨率和抗噪能力。

需要說明的是,由于ISAR中雷達信號的載頻較高,所以相鄰兩點間的相位差較大。比如f0=10 GHz,Tp=100μs,距離像采樣點數為1 024的條件下,相鄰兩點的相位差為0.8π。這種條件下,僅一個點的位置偏差就會導致復數GART算法的失效。

插值是解決該問題的有效途徑之一,通過插值可以降低相鄰兩點間的相位差,但是卻以計算量成平方倍增長為代價。例如,需要進行80倍插值才能在上述條件下使相鄰相位差小于0.01π,計算量增加6 400倍。因此,其計算量限制了復數GART不適用于對大目標大場景的成像處理。

實數GART和復數GART算法雖然有所差異,但是都處于GART方法的框架之內,基本流程相同,可以用圖3表示。

圖3 GART的算法流程圖

如式(7)和式(13)所示,在建立方程時需要利用自旋周期的估計值,當估計值越接近真實值時,成像質量越好。根據此特性,GART算法可以用于對自旋周期的粗估計值進行修正,其步驟如下:

步驟1:利用時頻分析技術得到自旋周期的粗估計值T;

步驟2:在T附近的一個區間內進行遍歷成像;

步驟3:計算每幅圖像的質量指標,如對比度、熵、像素最大值等;

步驟4:綜合分析圖像質量,最佳質量圖像對應的周期最接近真實自旋周期。

3 仿真與應用

3.1 仿真驗證

假設雷達中心頻率為10 GHz,帶寬為600 MHz,脈沖重復頻率為100 Hz,接收信噪比為10 dB,成像場景距雷達10 km。目標上存在4個散射點,坐標分別為(9,0),(-9,0),(0,6),(0,-6)且關于場景中心O以w=4πrad/s的速度旋轉。由于成像場景較大,采用實數GART算法即可,成像結果如圖4所示。

其他條件不變,重新設定散射點坐標為(0.3,0),(-0.3,0),(0,0.2),使得場景縮小30倍,且不再旋轉對稱。用實數GART和復數GART分別成像,其結果如圖5和表1所示。可見在添加相位信息之后圖像的質量和分辨率都有了極大提高,但是運算量也明顯增加。

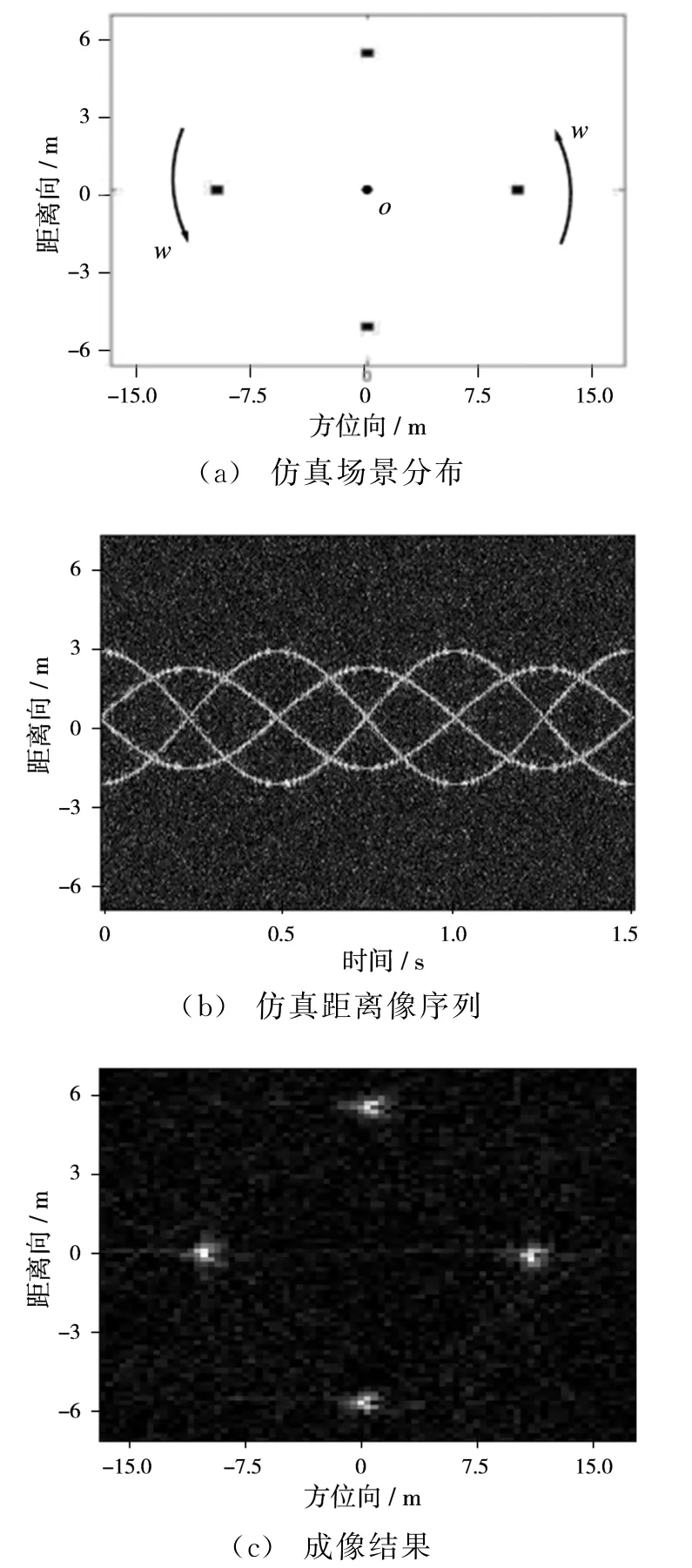
圖4 實數GART成像結果

圖5 小場景成像結果

表1 小場景條件下算法性能比較

3.2 飛機實測數據處理

第一段實測數據是AN-26運輸機的寬帶回波信號,AN-26的兩個機翼上各有一個4葉螺旋槳,直徑約為3 m,雷達的距離像分辨率為0.375 m,因此該螺旋槳屬于大目標,可以用實數GART對其進行處理,結果如圖6所示。

圖6(a)是距離多普勒算法成像結果,圖中有兩條明顯的方位向干擾帶,這是螺旋槳的自旋造成的微多普勒效應。采用Chirplet方法將高頻的運動信息從原信號中分離[9-10],并對其中的距離單元進行時頻分析得到時頻分布(圖6(b)),可以粗略估計出自旋周期約為0.045 s,再用2.3節中的方法進行精修正,從成像的熵曲線(圖6(c))和對比度曲線(圖6(d))得出自旋頻率為0.0475 s,用同樣的方法可以估計出另一個螺旋槳的自旋頻率為0.047 7 s。該飛機兩個螺旋槳的成像結果如圖7所示。從圖中可以清晰地看出,飛機發動機的螺旋槳是四頁片結構的,這將為目標識別提供更多有用的信息。

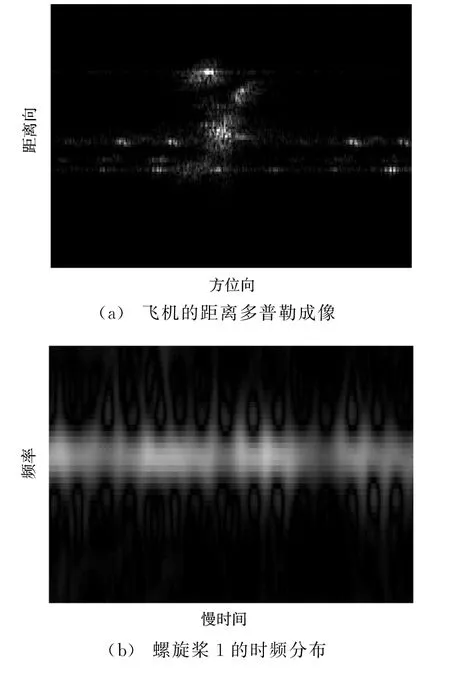
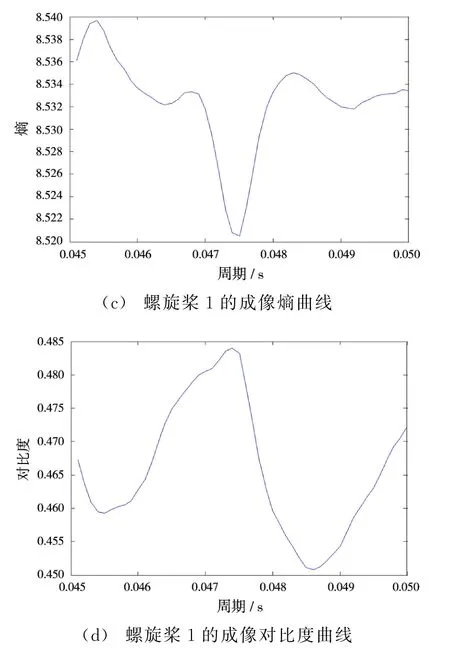
圖6 AN-26運輸機成像結果及螺旋槳旋轉頻率分析

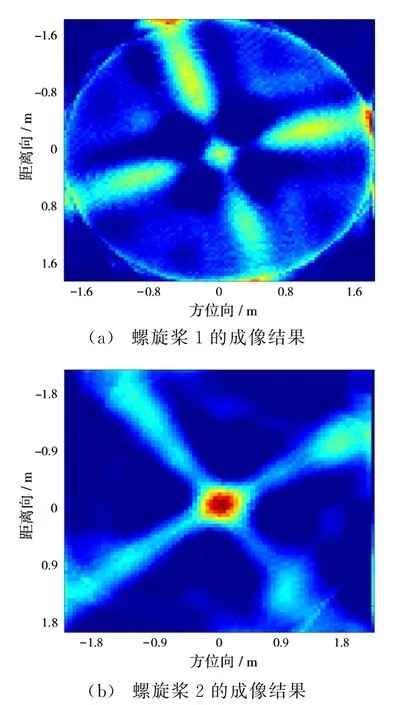
圖7 AN-26運輸機螺旋槳成像結果

4 結束語

本文提出了針對自旋目標寬帶成像的GRAT算法框架,在這個框架下給出了只考慮模值的實數GART算法和增加了相位信息的復數GART算法。其中實數GART算法運算速度快,適用于螺旋槳等較大的目標,而復數GART則具有分辨率高、抗噪性強的特點,可以用于微小自旋目標的成像。仿真和實測數據表明,GART是一種有效的自旋目標成像方法,可以用于目標結構的估計和自旋周期的精確修正。

GART算法提供的代數方法框架,有著廣泛的工程應用前景。一方面,通過GART算法可以獲得高速自旋目標的結構細節,為目標識別提供更多依據;另一方面,代數方法比解方法更容易與EM算法、OS算法、壓縮感知等現代計算方法相結合,以提高圖像重構的質量和效率。

[1]李星星,姚漢英,孫文峰,等.時間-距離像消隱情況下彈道目標平動補償[J].雷達科學與技術,2014,12(2):195-205.LI Xingxing,YAO Hanying,SUN Wenfeng,et al.Translational Motion Compensation of Ballistic Target in the Case of Time-Range Profile Blanking[J].Radar Science and Technology,2014,12(2):195-205.(in Chinese)

[2]張豪,李松,羅迎,等.彈道目標進動頻率精確提取方法研究[J].計算機仿真,2015,32(8):22-26.

[3]CHEN V C.Advances in Applications of Radar Micro-Doppler Signatures[C]∥2014 IEEE Conference on Antenna Measurements&Applications(CAMA),Antibes Juan-Les-Pins:IEEE,2014:1-4.

[4]SURESH P,THAYAPARAN T,OBULESU T,et al.Extracting Micro-Doppler Radar Signatures from Rotating Targets Using Fourier-Bessel Transform and Time-Frequency Analysis[J].IEEE Trans on Geoscience and Remote Sensing,2014,52(6):3204-3210.

[5]劉進.微動目標雷達信號參數估計與物理特征提取[D].長沙:國防科學技術大學,2010.

[6]BAI X R,ZHOU F,XING M D,et al.High Resolution ISAR Imaging of Targets with Rotating Parts[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(4):2530-2543.

[7]ANDERSEN A H.Algebraic Reconstruction in CT from Limited Views[J].IEEE Trans on Medical Imaging,1989,8(1):50-55.

[8]WANG G,JIANG M.Ordered-Subset Simultaneous Algebraic Reconstruction Techniques(OS-SART)[J].Journal of X-Ray Science and Technology,2004,12(3):169-177.

[9]LI J,LING H.Application of Adaptive Chirplet Representation for ISAR Feature Extraction from Targets with Rotating Parts[J].IEE Proceedings-Radar,Sonar and Navigation,2003,150(4):284-291.

[10]蔡洪,楊寧國,宋宏偉,等.自適應Chirplet信號分解用于ISAR目標三維轉動檢測[J].光電工程,2013,40(1):1-9.