庫侖定律適用條件的探析

庫侖定律適用條件的探析

陳偉孟胡繼超

(中國人民大學附屬中學北京100080)

摘 要：庫侖定律是高中物理的基礎知識和重點知識，而其適用條件則是教學中的難點且容易被忽略的環節.本文運用形象、直觀的物理模型來分析、闡述庫侖定律成立的3個條件，包括靜止與相對運動條件、點電荷條件和真空條件，有利于深化對庫侖定律物理本質的理解以及促進學生嚴謹物理思維的建立.

關鍵詞：庫侖定律適用條件靜止點電荷真空

收稿日期：(2014-07-03)

1問題的提出

18世紀末，法國物理學家庫侖通過一定的實驗和猜想總結出了兩個點電荷間相互作用的規律，即庫侖定律.庫侖定律是電學發展史上的第一個定量規律，從此，電學的研究從定性進入定量階段.定律是這樣闡述的：真空中兩個靜止點電荷間的相互作用力，與它們電荷量的乘積成正比，與它們距離的二次方成反比，作用力方向在它們的連線上.用公式來表示，就是

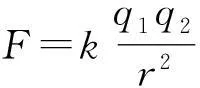
(1)

式中k是靜電力常量，實驗測量結果約是k=9.0×109N·m2/C2.從定律的描述可知“真空中”、“靜止的”和“點”電荷這3個定語，即庫侖定律成立的條件.

庫侖定律為什么需要這樣的限定？在教學中，也常有學生就這個問題表示困惑.該問題的詮釋屬于大學物理范疇，從高中教師的角度，應盡可能以形象易懂的中學物理圖像來解釋，以達到傳道授業解惑的目的，也為學生進一步向高等物理發展建立橋梁.下面將分別從“靜止的”、“點電荷”和“真空中”這3個方面進行庫侖定律的探析.

2關于靜止與相對運動問題

首先，探析關于“靜止的”適用條件.若是靜止的點電荷，周圍空間對此電荷而言沒有哪一個方向是特殊的，因此，如圖1所示正電荷的電場線，其電場分布會具有以點電荷為球心的球對稱性.

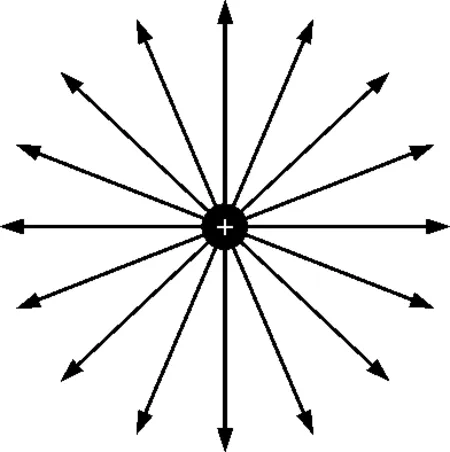
圖1　正電荷電場線

為了求出一個運動電荷的電場，根據運動的相對性，我們總可以找到該電荷在其中是靜止的一個參考系.在該參考系中，由于電場是靜止的，所以很容易得到電場分布，在此基礎上，采用狹義相對論基本原理就可以求出運動電荷的電場分布.不同參考系中場強的變換要回答這樣一個問題：如果在某一參考系S中，測得某時刻在一給定點處的場強為E，那么，在另一參考系S′中的相應時刻，相應位置處測得的場強E′將是怎樣的？為便于高中生理解，我們通過特例來討論這個問題.

如圖2(a)所示，在參考系S中有兩個靜止的平行帶電大平板，設板面垂直于z軸，沿著水平向右的x方向的長度為l0，板上分別帶有+Q和-Q的電荷.結合高中物理的平行板電容器知識

得出場強分布：在兩板外空間E=0，在兩板間空間

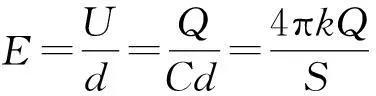
(2)

為求出垂直于帶電平板運動方向的場強變換關系，如圖2(b)所示，我們在另一參考系S′中再觀察電場，在S′系中，平行板面仍垂直于z軸，并以恒定速度v沿著x軸正方向運動.在S′系中的E′和E會有什么關系呢？

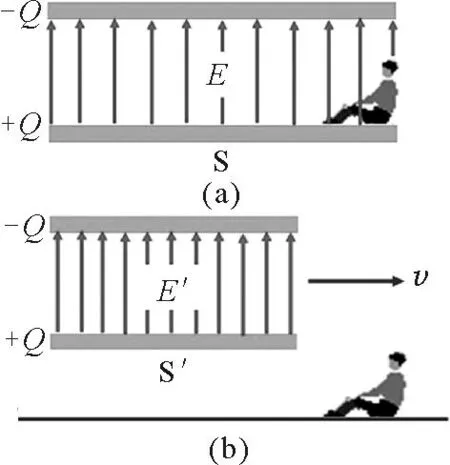
圖2

在S′系中，平行板在運動，根據狹義相對論長度的相對性，板的測量長度l應為

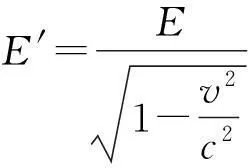
(3)

可直觀、形象地理解為電場線密度增大.

同理，如圖3，為了求出平行于平板運動方向的場強，可設想在S系中兩平板垂直于水平向右的x軸靜止，而在S′系中，兩板以速度v沿x軸的正方向運動.在S系中兩板靜止，板間場強為式(2).而在S′系中觀察時，兩板間距由于相對論效應變化，但板的寬度無變化，面積S無變化，而場強與極板間距d無關，即得E′=E.

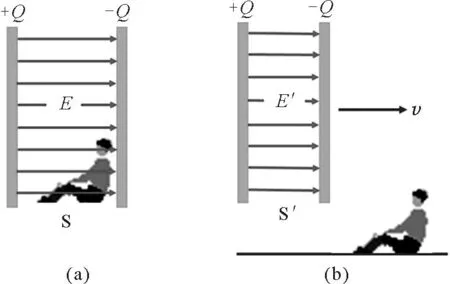
圖3

一般情況下，空間某點場強E的方向可以是任意的，根據場強疊加原理，可將E看成是沿x,y,z軸的3個分量的矢量和.對于任一分量，上述的相應變換仍是成立的.如圖4所示,靜止點電荷的電場在各個方向是均勻分布的；運動點電荷的電場不再具有球對稱性分布，而是從電荷運動的前方和后方，向著垂直于運動方向的平面附近聚集.電場線的疏密程度反映空間各處的場強大小，運動電荷的電場線分布在各個方向上不再一致.與運動場源電荷相同距離r但位于不同方向的各點場強大小就會不同，檢驗電荷所受的電場力大小也會不同.因此，運動場源電荷對其他檢驗電荷的作用力，不能再用式(1)統一描述，即庫侖定律不適用于運動場源電荷的情形.

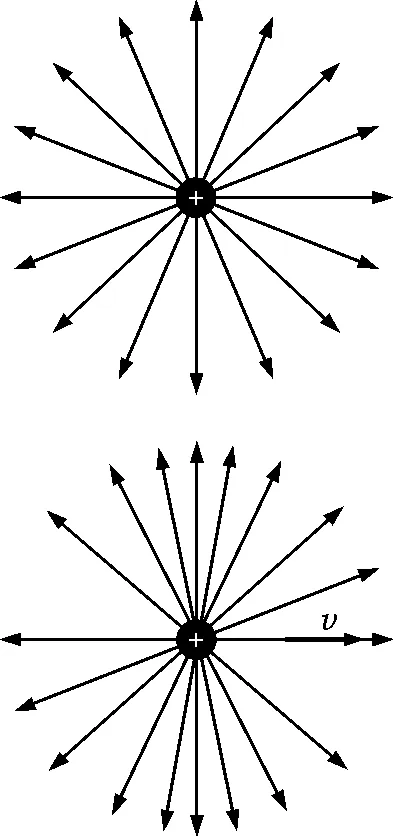
圖4

盡管如此，由式(3)也可看出，上述場強隨速度變化的效應只在高速運動電荷的情形下才會比較顯著.通常研究的帶電微粒的速度，與光速c相比，大多屬于低速的范疇，相對論效應可忽略不計，運動電荷仍等同靜止電荷來處理，因而在高中物理教學中并不強調該適用條件.

3關于“點電荷”問題

其次，分析關于“點電荷”的適用條件.先分析一道常見例題.

【例題】兩個帶等量電荷的銅球，相距較近且位置保持不變，設它們帶同種電荷時的靜電力為F1，它們帶異種電荷時(電荷量大小不變)的靜電力為F2，則F1和F2的大小關系為

A.F1=F2B.F1>F2

C.F1

“點電荷”是一理想的物理模型，與力學中的“質點”概念類似，即帶電體本身的幾何線度遠小于帶電體到觀察點的距離時，將帶電體簡化為一個帶一定電荷量的幾何點(實際上它本身的線度不一定很小).若是兩點電荷，在題中兩種情形下靜電力的大小應該是一樣的，只是同性相斥，異性相吸，方向不同而已.兩銅球“相距較近且位置保持不變”，不滿足“點電荷”條件，受到靜電排斥或吸引作用后，電荷會出現宏觀的移動，不再是均勻地分布在導體球的表面.如圖5，帶電球體間的質心距離L不再是兩電荷群之間的等效距離，會出現同性電荷間等效距離偏大而導致靜電力偏小，或異性電荷間等效距離偏小而導致靜電力偏大的情況，故答案為選項C.

圖5

分析發現，電場力的偏差來源于對帶電體而言庫侖定律中r值的不能準確確定，因此庫侖定律才要求研究的對象是“點電荷”.要討論類似情形下定量的場強和電場力大小，就需要把研究對象看作是具有一定電荷分布的帶電體來進行積分計算，那么，對每一點電荷而言庫侖定律還是適用的.該適用條件是高中物理的考核點.

4關于“真空”問題

最后，分析關于“真空”這一適用條件.如果兩電荷不是處于真空中，其周圍還有其他電荷或導體，兩點電荷除了受到彼此作用力之外還要受到其他電荷的作用力，實際的結果將由多個靜電力疊加得出.因此也就有了導體的靜電屏蔽效應，即導體的附加電場會將原電場抵消.若電荷周圍存在電介質，規律是類似的，電介質會發生極化現象，在介質中會出現極化電荷.極化電荷產生的附加電場一般比原電場弱，且與原電場方向相反，但終歸還是電荷間的作用.在導體或電介質中的場強，是由包括場源電荷、導體的感應電荷或電介質的極化電荷在內的多種電荷在“真空中”疊加的結果，等效于對庫侖定律式(1)中的常量k做出了相應的修正.定律中強調的“真空”條件，無非是對k=9.0×109N·m2/C2情形的限定，因此高中教學和教材中也并不強調這個適用條件.

5結束語

庫侖定律是高中重點知識，其適用范圍問題的探討則是更高程度的要求，但并非高中物理的考核要點，所以使得師生在教學中往往采取不關注的態度.若運用形象、直觀的物理模型來分析解答定律的3個適用條件，將有利于深化學生對庫侖定律物理本質的理解和促進學生嚴謹物理思維的建立，對于進一步促進學生對高等物理的學習和探究將大有裨益.

參 考 文 獻

1于軍，朱偉玲，吳登平.庫侖定律的教學價值.物理通報，2012(10):14～15

2吳波.庫侖定律只適用于“真空”嗎.物理教師，2012(4):17

3鄭慶璋，崔世治.相對論與時空.太原：山西科學技術出版社，2001