正弦波傳播介質中的質點在做簡諧運動嗎——對人教版《物理·選修3-4》波動部分的一點看法

正弦波傳播介質中的質點在做簡諧運動嗎
——對人教版《物理·選修3-4》波動部分的一點看法

張建斌柴春琪

(嘉興市第一中學浙江 嘉興314050)

摘 要：人民教育出版社2010年4月第3版《物理·選修3-4》認為,有正弦波傳播的介質中的質點在做簡諧運動.但筆者查閱了相關書籍后發現這一說法欠妥.本文將從平面簡諧波的波動方程和介質波的能量出發，分析機械波能量在空間上的分布、隨時間的變化與能量傳遞的實質，通過與簡諧運動進行對比，對新教材中關于機械波傳播過程中介質中質點的運動作新的描述,即“簡諧波是簡諧運動在介質中的傳播，介質中各質點做的是運動規律滿足正弦(或余弦)圖像的受迫振動”.

關鍵詞：受迫振動簡諧運動機械波能量傳遞

收稿日期：(2014-05-08)

普通高中課程標準實驗教科書《物理·選修3-4》(人民教育出版社2010年4月第3版)第27頁有這樣一句話，“介質中有正弦波傳播時，介質的質點在做簡諧運動”.但簡諧運動的能量在整個振動過程中是一個守恒量，簡諧運動的過程是動能和勢能相互轉化的過程，這樣做簡諧運動的介質中質點將無法實現傳遞能量的功能.本文主要闡述機械波的能量及其傳遞，并嘗試對新教材中關于機械波傳播過程中介質中質點的運動談一點自己的看法.

1平面簡諧波的波動方程

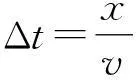
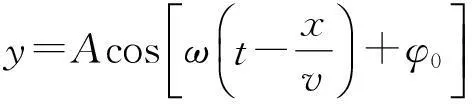
(1)

這就是平面簡諧波方程，它可以描述平面簡諧波在傳播方向上任意點的振動規律.

2介質中波的能量分布

一列波在彈性介質中傳播時，各體元都在平衡位置附近振動，所以具有動能，同時，各體元發生形變，又有彈性勢能.現以簡諧橫波為例，研究某體元的動能、勢能和總能量的變化規律.

2.1動能

在有簡諧橫波傳播的介質中，取一微元，根據平面簡諧波方程可得到其振動速度

設介質密度為ρ，微元體積為dV，則該體元的動能為

2.2形變勢能

我們選取的介質中的微元同時受到相鄰的微元的作用而發生剪切形變(即在力偶作用下，兩平行截面發生相對移動的形變)，如圖1所示.

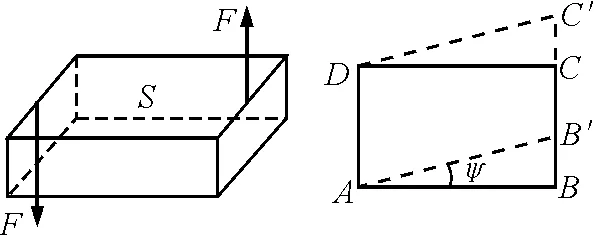
圖1

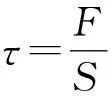
對于傳播橫波的介質中的微元而言，其剪切形變簡化為如圖2所示，有

所以選取的微元的形變勢能為

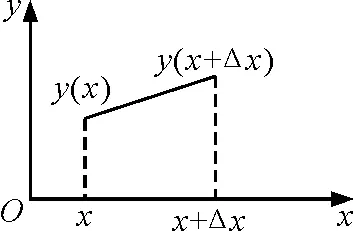
圖2

2.3總能量

彈性介質中橫波的波動方程可寫為

對式(1)偏導運算可得

即波動中某一微元的動能和勢能具有相同的數值，它們同時達到最大和最小.微元的總能量等于兩者之和，即

實際中，常用能量密度

也是時間和空間坐標的函數，體現出波的能量在時間和空間上的周期性.

3機械波能量及其傳遞的高中教學

基于高中學生的數學基礎，我們在進行這部分內容教學時，應切合學生實際，從學生已有知識基礎和能力水平去構建新的知識體系.筆者在實際輔導教學中先讓學生回顧彈簧拉伸形變和形變勢能，然后簡單介紹剪切形變和剪切形變勢能.接著如下過程.

3.1機械波能量在空間上的分布

機械波在傳播過程中，某時刻介質中某處質點的動能決定于該處質點的振動速度的大小，而勢能決定于該處介質的形變(即剪切形變)大小.

圖3所示為一列沿彈性繩傳播的簡諧橫波，分別在位于平衡位置的B和位于最大位移的A,C處，取相同長度Δx(Δx→0)的媒質微元來討論.

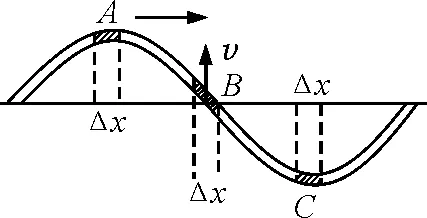
圖3

可以看出B處質點的振動速度最大，同時該處繩子的形變也最大，因此該處質點的動能和勢能為最大，其總能量也就最大.而對于A,C兩處的質點，此時它們的振動速度為零，且該處繩子的形變也趨于零，因此該處質點的動能和勢能都為零，即總能量也就最小(為零)，而A與B之間,B與C之間的質點的能量就介于最大和零之間.可見，同一時刻介質中各處的能量分布并不相同，在波峰和波谷處質點的能量最小(為零)，而在平衡位置處質點的能量最大.質點離平衡位置越近，能量就越大，即能量在波的傳播方向上呈現周期性的分布，隨著波形的向前傳播，這種能量分布的狀態也以波的傳播速度向前傳遞.

3.2機械波能量隨時間的變化

彈簧振子和單擺做自由的簡諧運動時，只有振動系統內部的動能和勢能的轉化，系統的總能量是守恒的，這表明振動系統不與外界交換能量，可認為是一個“保守系統”.在簡諧波的傳播過程中，每一質點的運動規律與簡諧運動相同，那么每一質點的能量是否也守恒呢?

圖4

3.3機械波能量傳遞的實質

如圖5所示為一列沿繩子向右傳播的簡諧橫波在某一時刻的波形圖.A,B,C為繩子上3個相鄰的質點，設波是由A傳向B，再傳向C的，則B質點的振動是由于A質點的振動使繩子發生形變而產生的彈力F帶動的，這個彈力對A做負功而對B做正功，使A質點不斷釋放能量，而使B質點不斷吸收能量，使能量從A傳遞給B.同理,B質點又不斷地向C質點傳遞能量.但每一質點在任一小段時間Δt(Δt→0)內，從前一質點吸收的能量并不等于向后一質點釋放的能量，如圖5中的質點B，由于兩側介質的形變大小不同，兩側質點A,C對它的彈力也就不同，左側形變小,彈力小，右側形變大,彈力大，因此在這一時刻附近的一小段時間Δt(Δt→0)內A對B做的正功小于B克服C做的功，也就是說B從A吸收的能量小于B向C釋放的能量.因而B向上離開平衡位置的過程中總能量是減少的.同理，在B返回平衡位置的過程中總能量又是增加的.這樣通過介質之間的相互作用力做功，使每一質點周期性地積累能量和釋放能量，實現了能量隨波的傳遞.

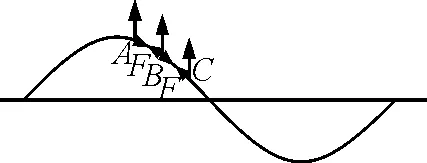
圖5

綜上，機械波在傳播過程中，每一時刻介質中各處的能量(即能量密度)在波的傳播方向上呈現周期性分布，是不均勻的，而每一質點的能量也是隨時間周期性變化的，是不守恒的，能量的傳遞是通過質點之間的相互作用力做功來實現的.

4對教材中 “波動”部分的一點看法

4.1關于簡諧運動

質點在某位置所受的力(沿運動方向受的力)為零，則此位置稱為平衡位置.若作用于質點的力總與質點相對平衡位置的位移(線位移或角位移)成正比，且指向平衡位置，則此作用力稱為線性回復力.以平衡位置為原點，以x表示質點相對于原點的位移，線性回復力fx=-κx，κ是正常量.力fx是質點位移x的線性函數，且與位移x反向，即促使質點返回平衡位置.質點在線性回復力作用下圍繞平衡位置的運動叫做簡諧運動.

x=Acos(ω0t+α)=Asin(ω0t+α′)

這就是簡諧運動的運動學方程，其運動圖像為余弦(或正弦)圖線.

教材對簡諧運動的定義，“如果質點的位移與時間的關系遵從正弦函數的規律，即它的振動圖像(x-t圖)是一條正弦曲線，這樣的振動叫做簡諧運動”，這個定義顯然不夠.教材既然通過振動圖像來定義簡諧運動，則必須同時應說明圖像x=Asin(ω0t+α′)中的ω0是由振動系統本身的性質決定的.這樣也有助于學生區分簡諧運動與有簡諧波傳播的介質中質點的運動.