小黃魚(Pseudosciaena polyactis)形態性狀與體質量的相關性及通徑分析*

劉 峰 陳 琳 樓 寶 詹 煒 陳睿毅 徐冬冬王立改 徐麒翔 馬 濤 毛國民

(1. 浙江省海洋水產研究所 舟山 316021; 2. 浙江海洋大學 舟山 316022; 3. 象山縣水產技術推廣站 寧波 315700;4. 浙江省海水增養殖重點實驗室 舟山 316021)

小黃魚(Pseudosciaena polyactis, Bleeker)又名小鮮、黃花魚等, 隸屬于硬骨魚綱 Osteichthyes、石首魚科Sciaendae、黃魚屬Larimichthys, 是中國近海漁業的重要經濟種類(李建生等, 2009), 其肉質鮮美、營養價值高, 曾與大黃魚(Larimichthys crocea)、墨魚(Sepiella maindron)、帶魚(Trichiurus japonicas)并稱為我國“四大海產”。小黃魚為暖溫性底層魚類, 具有規律性洄游習性(Jin et al, 1996), 3月份自越冬場開始生殖洄游, 于 4—5月在沿岸淺水區產卵(徐獻明等,2012)。另外, 小黃魚屬于廣溫、廣鹽性魚類(謝立峰等, 2006), 但其進行產卵時對水溫要求比較嚴格, 而鹽度條件則可小幅度波動(劉勇等, 2007)。

小黃魚作為我國四大海產之一, 具有其特有的經濟重要性, 自20世紀70年代以來, 由于過度捕撈、環境污染、氣候變化等原因, 小黃魚產量逐年減少,Chen等(1997)在研究渤海和黃海的漁業資源分布時,發現小黃魚資源已經從以前接近 20%的漁獲量銳減到2%。進入20世紀90年代以來, 由于禁漁區、禁漁期和伏季休漁措施的實施, 小黃魚產量逐漸恢復上升(Froese et al, 2014)。然而, 產量增加的部分主要是當齡魚(林龍山等, 2004a), 因此, 雖然小黃魚漁獲量有所增加, 但是其年齡組成序列縮短、性成熟提前、漁獲小型化的資源衰退現象非常明顯(林龍山等,2004b)。為了避免小黃魚像大黃魚一樣出現野生資源幾乎滅絕的現象, 需要采取措施對小黃魚群體進行有效的管理和保護(Wang et al, 2015)。采取小黃魚的人工繁殖和良種選育工作是恢復小黃魚的漁業資源,滿足人們日益增長的消費需求的重要手段。近年來,國內已經相繼開展小黃魚的人工繁育工作, 試圖通過增殖放流補充海洋中小黃魚資源。謝立峰等(2006)于 2003年開展了小黃魚親魚培育技術的研究; 徐獻明等(2012)于 2012年對近海捕獲的小黃魚親本采取人工授精法獲得受精卵, 開展小黃魚的人工繁殖研究, 隨后又對近海捕獲的小黃魚幼魚進行人工培育研究(徐獻明等, 2014), 但是由于多方面原因, 上述研究最終未能取得小黃魚的規模化繁育突破。2014年, 浙江省海洋水產研究所科研人員對野生小黃魚進行馴化養殖, 親魚越冬及強化培育后, 于 2015年開展小黃魚親魚的人工催產授精、苗種培育等研究,成功獲得小黃魚苗種2.5萬尾, 實現了小黃魚的人工繁育。作為“四大海產”中, 第三種人工繁育取得成功的魚類, 小黃魚人工繁殖技術的重大突破, 對漁業資源的恢復與利用意義重大, 將為下一步增殖放流和人工養殖提供新品種。

我國從20世紀50年代末就已開始海水魚類人工繁殖研究, 到目前為止有很多種魚類獲得成功, 并已經培育出具有優良性狀新品種(全國水產技術推廣總站, 2010, 2014), 如大黃魚“閩優1號”、“東海1號”,大口黑鱸“優鱸1號”等, 這些新品種均取得了較好的經濟效益。相比于上述魚類, 小黃魚的人工繁殖及良種培育研究還處于剛剛起步階段。在魚類生長性狀的遺傳育種過程中, 具有直觀性和可度量性的體質量是常用的目標性狀(樓允東, 1999; 張敏瑩等, 2010)。但是在實際生產中, 對于體質量的準確測量往往存在一定難度, 而如果是對與體質量存在一定相關性的形態性狀進行測量, 則較為準確快捷, 因此有必要通過相關分析(Ezekiel, 1941)方法衡定不同形態性狀與體質量的關聯程度, 然后采用回歸分析(Land, 1969)和通徑分析(Efroymson, 1960)方法剖析各個形態性狀對體質量的影響方式和作用大小, 這一研究方法已經在蝦類(劉小林等, 2004; 王志錚等, 2011; 栗志民等, 2011)、蟹類(耿緒云等, 2007)、貝類(Ahmed et al,2000; 王明華等, 2014; 張嘉麗等, 2014)及魚類(王新安等, 2008; 楊貴強等, 2011)等水產動物中開展研究。

由于小黃魚人工繁殖研究剛剛取得突破, 許多研究工作尚未開展, 小黃魚形態性狀與體質量之間關系的研究還未見報道。因此, 本研究對繁殖成功的小黃魚養殖群體進行體質量和形態性狀的測量和統計分析, 研究形態性狀與體質量的相關性并進行通徑分析, 衡量各個形態性狀與體質量的關聯程度, 并深入剖析各形態性狀對體質量直接作用和間接作用,確定影響小黃魚體質量的主要形態性狀及其決定作用, 以期發現與體質量相關性較高的形態性狀, 建立體質量增長的多元回歸方程, 為開展小黃魚的選擇育種提供參考資料、奠定理論基礎。

1 材料與方法

1.1 實驗材料

以2015年于舟山市西軒漁業科技島通過野生小黃魚繁殖獲得的后代群體為研究材料, 待魚苗生長至4.5月齡時, 隨機取樣729尾。用游標卡尺準確測量每一尾實驗魚的8個形態性狀, 包括全長(X1, cm)、體長(X2, cm)、頭長(X3, cm)、軀干長(X4, cm)、尾部長(X5, cm)、尾柄長(X6, cm)、尾柄高(X7, cm)、體高(X8, cm),精確至0.01 cm。用電子天平準確稱量體質量(Y, g), 精確至0.01 g。各個形態性狀測量方法如圖1所示。

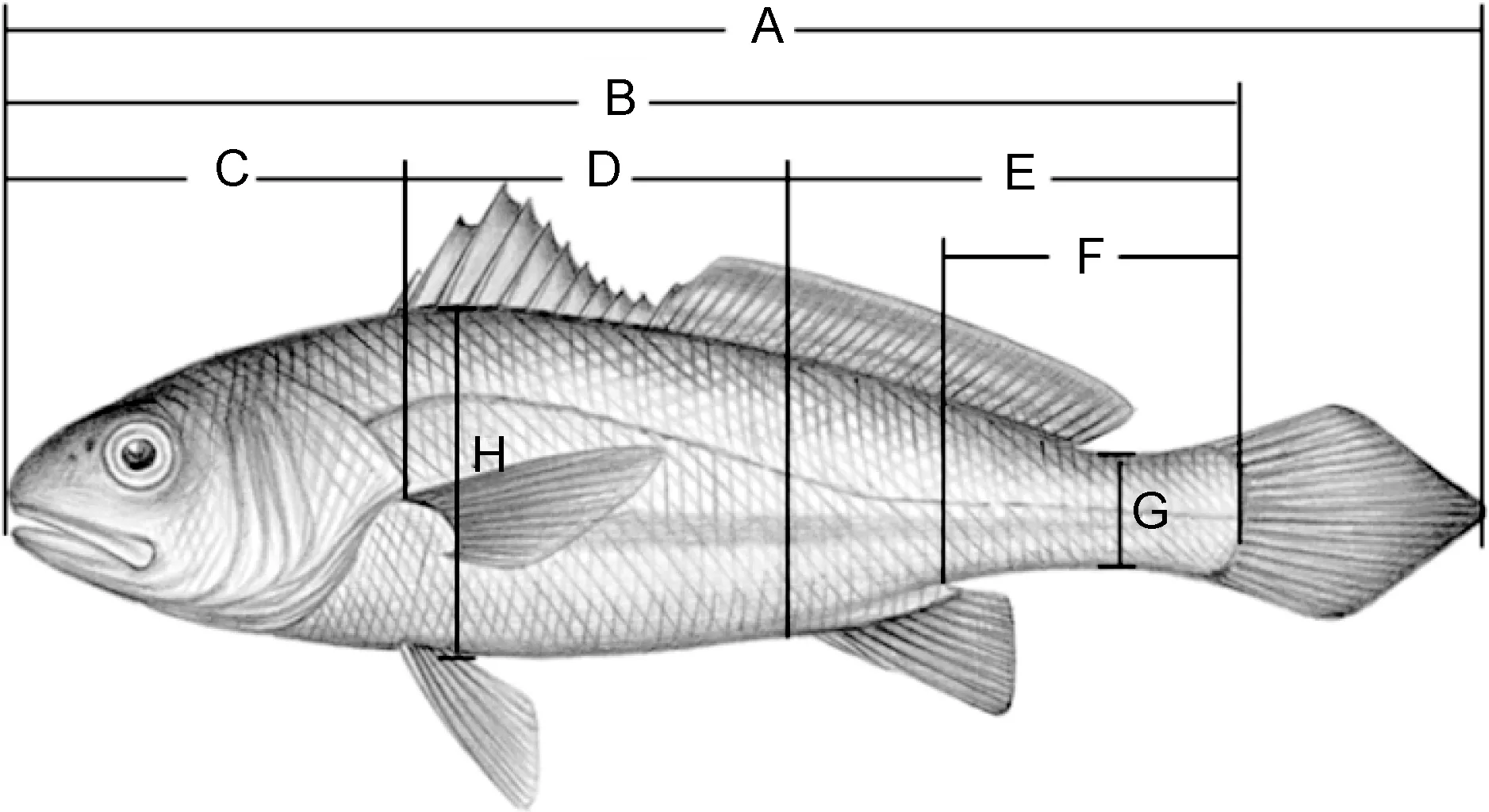
圖1 小黃魚形態性狀測量部位示意圖Fig.1 Sketch of mensuration part of morphometric traits for P.polyactis

1.2 分析方法

運用SPSS 17.0軟件對形態性狀和體質量進行描述性統計, 統計參數包括各個性狀的最小值、最大值、平均值、標準差、標準誤、變異系數等。采用Pearson法對各性狀進行表型相關分析; 在表性相關分析的基礎上運用逐步引入-剔除法建立形態性狀與體質量的多元線性回歸方程, 進行形態性狀對體質量的通徑分析, 剖析各形態性狀對體質量的直接作用(通徑系數)和間接作用(間接通徑系數), 間接通徑系數公式如下:

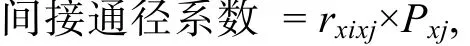
其中,rxixj為形態性狀Xi和Xj之間的Pearson相關系數;Pxj為性狀Xj對體質量的通徑系數。

利用相關系數和通徑系數, 根據下列公式計算形態性狀對體質量的決定系數:

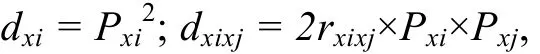
其中,dxi為形態性狀Xi對體質量的決定系數;dxixj為某兩個形態性狀Xi和Xj對體質量的共同決定系數;rxixj為兩個形態性狀Xi和Xj之間的Pearson相關系數;Pxi為性狀Xi對體質量的通徑系數;Pxj為性狀Xj對體質量的通徑系數。

2 結果

2.1 表型數據描述性統計

對所有形態性狀和體質量數據進行描述性統計,結果列于表1。

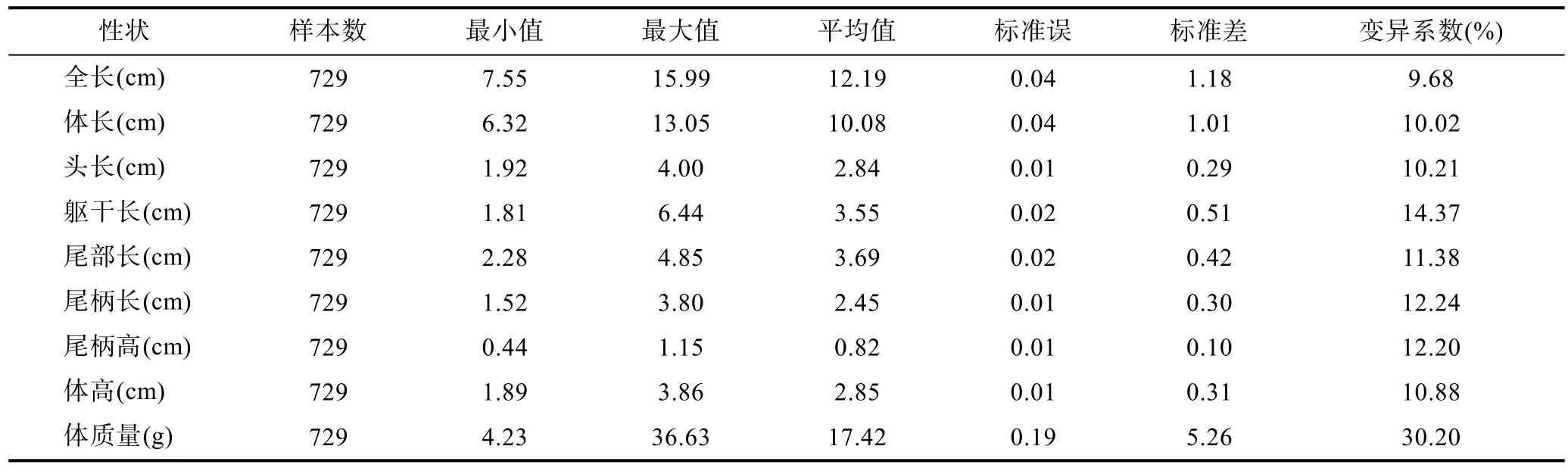
表1 表型性狀的描述性統計Tab.1 The descriptive statistics of phenotypic traits

從表1中可以看出, 所有性狀中, 體質量的變異系數最大, 達30.20%; 8個形態性狀的變異系數則相對較小, 并且相互之間差異不是很大, 分布在 9.68%—14.37%之間, 其中最大的為軀干長, 最小的為全長。計算各個性狀數據的標準誤可以發現, 所有性狀的標準誤均較小, 表明本次隨機采集的樣本各參數對總體的估計可靠性較高。所有性狀中, 除了全長, 其余性狀測量數據變異系數均在 10%以上, 說明不同個體之間生長速度方面存在一定差異, 這是進行選擇育種的重要前提。

2.2 性狀之間的相關性分析

對小黃魚的形態性狀和體質量進行表型相關性分析, 獲得了所有性狀之間的相關系數, 結果列于表2。從表中可以看出, 各性狀之間均表現為極顯著水平的表型相關性(P＜0.01), 但是不同性狀之間相關系數差別較大, 在 0.310—0.943范圍內。形態性狀相互間的相關性分析中, 全長和體長的相關性最高, 其相關系數為 0.943; 而頭長與軀干長的相關性最低, 其相關系數僅有0.310。形態性狀與體質量之間的相關性分析結果顯示, 8個形態性狀中, 全長與體質量相關性最高, 其相關系數高達 0.942, 而軀干長與體質量之間的相關性則最低, 其相關系數為0.684。

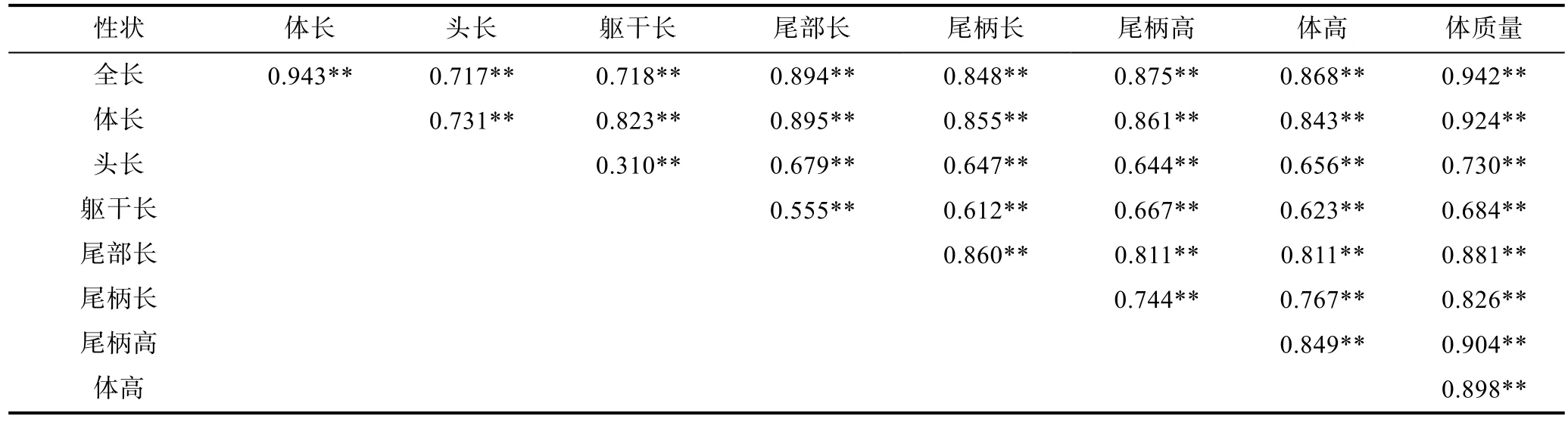
表2 表型性狀之間的相關性分析及顯著性檢驗Tab.2 Correlation analyses and significance test on phenotypic traits

2.3 形態性狀與體質量的多元回歸分析

本研究在相關分析的基礎上, 采用多元回歸的分析方法研究了形態性狀對體質量的作用, 同時進行自變量的共線性診斷, 以免自變量之間存在嚴重共線性問題, 影響多元回歸模型的可靠性。檢驗結果顯示全長性狀存在嚴重共線性, 所以將全長性狀剔除后, 對其余變量進行多元回歸分析。表3列出了采用逐步引入-剔除自變量的方法進行回歸分析過程中各種參數的變化情況。表中數據顯示, 隨著自變量的加入, 回歸方程R值在逐漸增加, 從 0.924增加到0.962, 估計的標準誤也由2.011逐漸降低為1.437, 表明模型估計的準確性在不斷增加, 也就說明模型中自變量的增加對于更加準確地解釋體質量具有重要作用。

表3 模型匯總Tab.3 The model summary

采用逐步法構建多元回歸方程, 獲得了方程中每個自變量的偏回歸系數(即非標準化回歸系數), 對各個自變量的偏回歸系數進行顯著性檢驗, 檢驗結果列于表4。

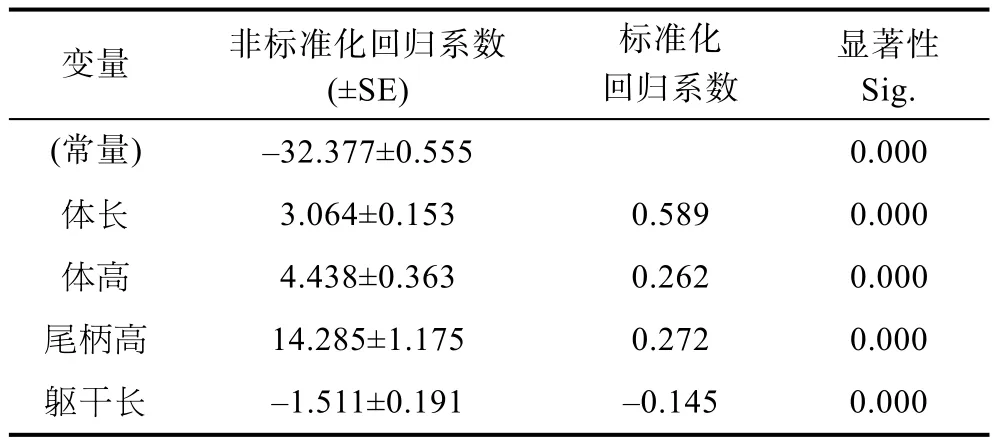
表4 回歸系數結果Tab.4 The calculation result of regression coefficient

表 4中數據顯示, 對截距–32.377的檢驗結果為極顯著(P＜0.001), 對各偏回歸系數的顯著性的檢驗結果為體長(X2)、軀干長(X4)、尾柄高(X7)和體高(X8)均達極顯著水平(P＜0.01), 說明截距和這 4個形態性狀的偏回歸系數與0之間均存在顯著性差異, 可認為所求的多元線性回歸方程成立。采用F檢驗的方法對構建的多元回歸方程進行顯著性檢驗(表 5), 檢驗結果顯示, 回歸方程達到極顯著水平(F= 2254.455,P＜0.01), 說明該回歸方程具有統計意義; 被納入模型中的 4個自變量對體質量的決定系數(R2)為 0.926(表 3), 說明模型中所納入的 4個形態性狀對體質量有較大的決定作用。由此得出, 以形態性狀為自變量,體質量為因變量的多元回歸方程可寫為:Y= –32.377+ 3.064X2– 1.511X4+ 14.285X7+ 4.438X8。

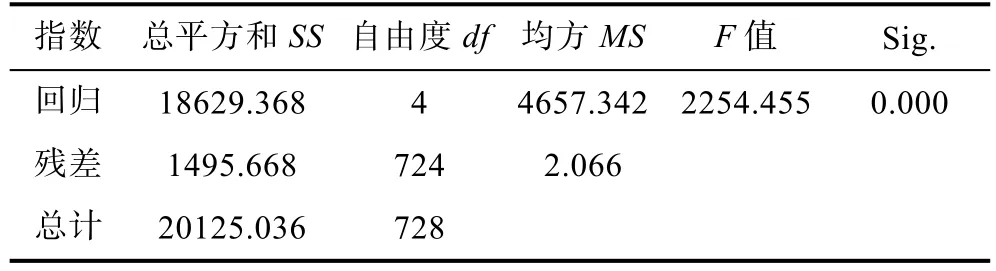
表5 多元回歸方程的方差分析Tab.5 Analysis of variance of multiple regression equations

2.4 形態性狀與體質量的通徑分析

本次研究共測量了8個形態性狀, 經共線性診斷剔除了共線性嚴重的全長及對體質量影響不顯著的 3個形態性狀, 剩余4個性狀對體質量的影響達到極顯著水平(P＜0.01), 所以回歸方程中包含了該4個形態性狀作為自變量。對回歸方程中的偏回歸系數進行標準化后可獲得各性狀對體質量的通徑系數(表 4), 檢驗結果表明,4個形態性狀對體質量的通徑系數(直接作用)均有統計學意義(P＜0.05), 但是不同形態性狀對體質量的直接作用有所差異, 最大高達0.589, 最小為負值–0.145。直接作用由大到小排序依次為: 體長＞尾柄高＞體高＞軀干長。由此可知, 不同形態性狀對體質量的影響作用存在很大差別, 所以, 采用通徑分析的方法進行各個性狀對體質量的直接和間接作用的深入剖析具有重要意義。

根據通徑分析原理將形態性狀對體質量的影響效應剖分為直接作用(通徑系數)和間接作用(間接通徑系數), 結果列于表6。通徑系數反映自變量對依變量的直接作用, 在所研究的目標性狀中, 體長對體質量的通徑系數最大, 即其對體質量的直接作用最大,尾柄高對體質量的直接作用次之, 而軀干長對體質量的直接作用為負值, 值為–0.145。

表6 相關系數分解Tab.6 Decomposition of correlation coefficient

分析間接通徑系數可以發現, 小黃魚的體長通過其余形態性狀作用于體質量的間接通徑系數各不相同, 比較發現, 所有間接作用中, 尾柄高通過體長對體質量的間接作用最大(0.507)。結合性狀之間的表型相關性分析得出, 與體長相關性越高的形態性狀,體長通過該性狀對體質量起作用的間接通徑系數越大, 這一結果可以通過間接通徑系數的計算公式進行解釋。分析其它幾個形態性狀也可得出同樣規律。另外還可發現, 軀干長通過其它形態性狀對體質量的間接作用均大于其自身的直接作用。由于軀干長對體質量是負影響作用, 所以當其它性狀通過其作用于體質量時均顯示負影響, 這一結果同樣可以由間接通徑系數計算公式進行解釋。除了體長性狀, 其余三個性狀通過其它性狀對體質量的間接作用的總和均遠遠大于其自身對體質量的直接作用。其它性狀通過體長作用于體質量的間接作用均大于通過其它形態性狀的作用。表中各形態性狀對體質量的方差膨脹因子(variance inflation factor, VIF)數值均小于經驗值(VIF=10), 表明各形態性狀直接和間接作用的估計和回歸模型的構建均無共線性的影響, 因而本次分析結果是準確可靠的。

2.5 形態性狀對體質量的決定程度

各形態性狀對體質量的決定系數見表 7。其中,對角線上為各形態性狀對體質量的單獨決定系數,對角線以上為兩個性狀對體質量的共同決定系數。比較發現, 幾個形態性狀對體質量的單獨決定系數差別較大。比較而言, 體長的決定作用最大, 其決定系數為 0.347; 其次為尾柄高; 而軀干長的決定系數最小, 僅為0.021。在兩個性狀共同決定系數中, 體長和尾柄高對體質量的共同決定作用最大, 決定系數為0.276。單獨決定系數和兩性狀共同決定系數的總和等于總的決定系數, 為 0.927。根據總決定系數可計算出剩余因子e=0.270, 這個值還比較大, 說明對小黃魚體質量有影響的自變量除了本次研究的幾個形態性狀之外, 還有一些影響較大的因素沒有考慮到,因此對小黃魚體質量影響因素的全面分析還有待于進一步研究。

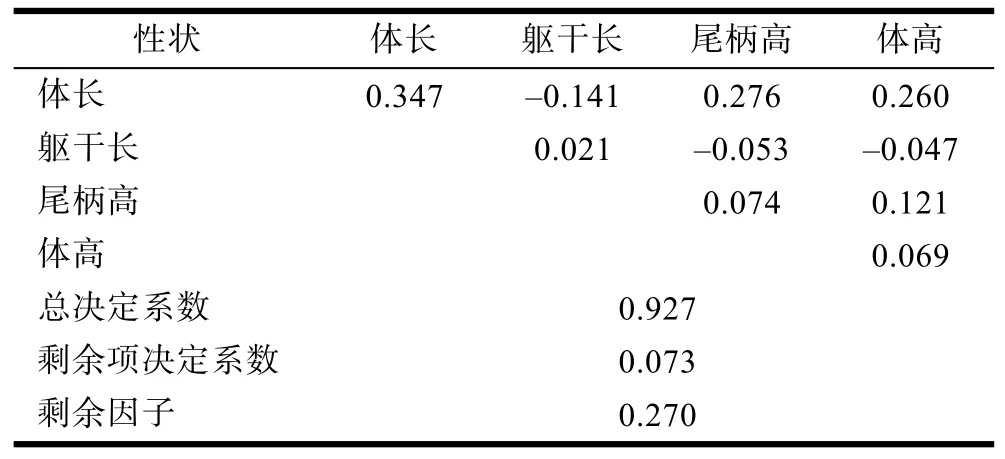
表7 養殖小黃魚形態性狀對體重的決定系數Tab.7 The determinant coefficient of the morphometric traits on the body weight of P. polyactis

3 討論

3.1 小黃魚形態性狀與體質量相關性

在魚類的選擇育種中, 生長性狀的主要衡量指標為體質量, 其次即為全長、體長等一些可測量的形態性狀。本研究對小黃魚的形態性狀和體質量性狀之間的關系進行探討。首先對形態性狀和體質量進行相關分析, 確定形態性狀與體質量之間的相關關系, 結果顯示, 8個形態性狀與體質量間的相關系數最小為0.684, 均達到極顯著水平(P＜0.01), 說明在小黃魚的選擇育種中, 對形態性狀進行選擇, 可以實現對體質量的間接選擇。本研究中, 與體質量相關性最高的前4個形態性狀依次為: 全長＞體長＞尾柄高＞體高。這一排序結果與劉賢德等(2010)對大黃魚、Nguyen等(2010)和 Tr?ng等(2013)對吉富羅非魚形態性狀與體質量相關性的研究結果存在一定差異。說明不同魚類的形態性狀與體質量之間的關系存在種群特異性。

3.2 通徑分析必要性

本次研究中, 所有形態性狀與體質量均為極顯著相關(P＜0.01), 但是經過共線性檢驗發現全長存在嚴重共線性, 所以需要將其剔除。對剩余7個形態性狀與體質量進行了通徑分析, 結果表明, 對體質量的直接影響僅4個形態性狀達到極其顯著水平, 其余3個性狀對體質量影響不顯著(P＞0.05)。由此可見, 通過性狀間的相關性分析只能得知形態性狀與體質量之間總的關聯性, 無法區分形態性狀對體質量的直接作用和通過其它形態性狀對體質量的間接作用,因此, 不能全面考察變量間的相互關系。多元回歸分析在一定程度上能夠消除變量之間的混淆, 但由于偏回歸系數帶有單位, 無法直接進行比較, 需要對偏回歸系數進行標準化處理, 即進行通徑分析。通徑分析克服了相關分析與回歸分析的不足, 能夠真實反映各自變量和依變量的關系(王新安等, 2008)。通徑分析可以獲得各個形態性狀的通徑系數和間接通徑系數, 其中, 通徑系數表示形態性狀對體質量直接作用的大小(耿緒云等, 2007; 王明華等, 2014), 而間接通徑系數則表示某個形態性狀通過其它形態性狀對體質量實現間接作用的大小(何小燕等, 2009)。因此,采用通徑分析的方法進行形態性狀對體質量的直接作用和間接作用深入剖析, 從中找出影響小黃魚體質量的主要因素非常必要。

3.3 回歸分析和通徑分析

剔除共線性嚴重的全長后, 以7個形態性狀作為自變量, 體質量為因變量通過逐步引入-剔除的方法對形態性狀和體質量進行多元回歸分析, 結果顯示,體長、軀干長、尾柄高及體高與體質量的標準化回歸系數極顯著, 而不顯著的頭長、尾部長和尾柄長性狀則被剔除, 以偏回歸系數(非標準化回歸系數)顯著的4個形態性狀為自變量, 體質量為因變量構建多元回歸方程, 準確描述了形態性狀與體質量之間的真實關系。回歸方程中包含的形態性狀對體質量總決定系數高于主要決定因子臨界點 0.85(王新安等, 2011),說明所篩選的形態性狀能在很大程度上反映體質量增長量的變異; 已剔除的性狀對體質量增長變異影響不大, 保留下來的形態性狀確定為體質量增長的主要因素。但是剩余因子計算結果顯示, 除了本次研究涉及的形態性狀, 還存在著其它對體質量有影響的性狀未找到, 因此, 需要增加測量性狀的數目, 使得對小黃魚體型描述更加詳細; 還需要考慮多個性狀間的比例關系, 建立一個更完善的模型, 以此提高形態性狀與體質量的相關性, 這些都需要今后進一步深入的研究。

構建的多元回歸方程經檢驗達到極顯著水平(P＜0.01), 說明回歸方程有意義, 可見對于小黃魚而言, 形態性狀作為自變量對體質量進行預測和估計是恰當的, 這一結果在大黃魚(劉賢德等, 2008,2010)、大口黑鱸(何小燕等, 2009)、羅非魚(董在杰等,2010; 肖煒等, 2015)等其它鱸形目及半滑舌鰨(劉峰等, 2015)、牙鲆(王凱等, 2008)、大菱鲆(王新安等,2008)等鰈形目魚類中均已得到證實。因此, 通過形態性狀進行小黃魚體質量方面的選育是可行的。近年來在多種魚選育中開展了結合形態性狀的選育研究。如,劉賢德等(2010)研究了13月齡和20月齡大黃魚形態性狀對體質量的影響, 結果顯示, 這兩個生長時期,均是體高對體質量的直接作用最大(0.522, 0.394); 王新安等(2013)研 究紅鰭東方 魨 發現形態性狀中體周長對體質量的直接影響(0.533)最大; 而本次研究中, 養殖小黃魚形態性狀中對體質量直接作用最大的是體長(通徑系數: 0.589), 與上述報道有所不同, 并且通徑系數大于上述報道。

4 結論

本文對 729尾養殖小黃魚的形態性狀與體質量之間的關系進行了研究, 包括形態性狀與體質量的相關性分析、回歸分析及通徑分析。結果顯示, 8個形態性狀與體質量均表現為極顯著相關性, 但是不同性狀與體質量的相關性差別較大, 其中, 最高的性狀是全長; 回歸分析結果顯示, 全長存在嚴重的共線性, 所以將其剔除后分析得出, 有4個形態性狀均與體質量存在顯著的線性關系, 以其為自變量, 體質量為因變量構建了多元回歸方程: Y = –32.377 + 3.064 X2– 1.511 X4+ 14.285 X7+ 4.438 X8; 經過通徑分析獲得各形態性狀對體質量的直接作用和間接作用, 其中體長對體質量直接作用最大(0.589); 尾柄高通過體長對體質量的間接作用最大(0.507)。找出對體質量影響最大的幾個形態性狀, 有助于實現對體質量的間接選擇, 獲得正確的親本, 這對于小黃魚的資源保護和恢復, 以及開展規模化的人工養殖及優良品種選育均有重要意義。

王 凱, 劉海金, 劉永新等, 2008. 牙鲆形態性狀對體重的影響效果分析. 上海海洋大學學報, 17(6): 655—660

王志錚, 吳一挺, 楊 磊等, 2011. 日本沼蝦(Macrobrachium nipponensis)形態性狀對體重的影響效應. 海洋與湖沼,42(4): 612—618

王明華, 鐘立強, 蔡永祥等, 2014. 黃顙魚形態性狀對體重的影響效果分析. 浙江海洋學院學報: 自然科學版, 33(1):41—46

王 新 安, 馬愛 軍, 莊 志 猛 等, 2013. 紅 鰭 東 方 鲀 (Takifugu rubripes)形態性狀對體重的影響效果. 海洋與湖沼, 44(1):135—140

王新安, 馬愛軍, 許 可等, 2008. 大菱鲆幼魚表型形態性狀與體重之間的關系. 動物學報, 54(3): 540—545

王新安, 馬愛軍, 黃智慧等, 2011. 大菱鲆(Scophthalmus maximus)大規模家系選育優良家系的生長發育規律. 海洋與湖沼, 42(2): 266—273

全國水產技術推廣總站, 2010. 2010水產新品種推廣指南. 北京: 中國農業出版社

全國水產技術推廣總站, 2014. 2014水產新品種推廣指南. 北京: 中國農業出版社

劉 勇, 嚴利平, 程家驊, 2007. 2003年東海北部和黃海南部外海小黃魚產卵群體的分布特征及其與水溫、鹽度的關系.中國水產科學, 14(7): 89—96

劉 峰, 陳松林, 劉肖峰等, 2015. 半滑舌鰨 3個形態性狀與體質量的相關及通徑分析. 海洋學報, 37(4): 94—102

劉小林, 吳長功, 張志懷等, 2004. 凡納對蝦形態性狀對體重的影響效果分析. 生態學報, 24(4): 857—862

劉賢德, 蔡明夷, 王志勇等, 2008. 閩-粵東族大黃魚生長性狀的相關與通徑分析. 中國海洋大學學報, 38(6): 916—920

劉賢德, 蔡明夷, 王志勇等, 2010. 不同生長時期大黃魚形態性狀與體重的相關性分析. 熱帶海洋學報, 29(5):159—163

李建生, 林龍山, 程家驊, 2009. 東海北部秋季小黃魚分布特征及其與底層溫度和鹽度的關系. 中國水產科學, 16(3):348—356

楊貴強, 徐紹剛, 王躍智等, 2011. 硬頭鱒幼魚部分形態性狀和體重的關系. 動物學雜志, 46(1): 16—22

肖 煒, 李大宇, 鄒芝英等, 2015. 湘湖品系尼羅羅非魚形態性狀對體重的影響. 西南農業學報, 28(1): 433—438

何小燕, 劉小林, 白俊杰等, 2009. 大口黑鱸形態性狀對體重的影響效果分析. 水產學報, 33(4): 597—603

張敏瑩, 劉 凱, 段金榮等, 2010. 太湖秀麗白蝦形態性狀對體重影響的通徑分析. 中國農學通報, 26(21): 417—421

張嘉麗, 王慶恒, 鄧岳文等, 2014. 斧文蛤(Meretrix lamarchii)形態性狀對體質量的影響效果分析. 漁業科學進展, 35(6):110—113

林龍山, 程家驊, 2004a. 東海區小黃魚漁業生物學現狀的分析. 中國海洋大學學報, 34(4): 565—570

林龍山, 程家驊, 任一平等, 2004b. 東海區小黃魚種群生物學特征的分析. 中國水產科學, 11(4): 333—338

耿緒云, 王雪惠, 孫金生等, 2007. 中華絨螯蟹(Eriocheir sinensis)一齡幼蟹外部形態性狀對體重的影響效果分析.海洋與湖沼, 38(1): 49—54

栗志民, 劉志剛, 王 輝等, 2011. 企鵝珍珠貝(Pteria penguin)主要經濟性狀對體重的影響效果分析. 海洋與湖沼, 42(6):798—803

徐獻明, 張志勇, 吳建平等, 2012. 小黃魚人工繁育試驗. 水產養殖, 33(12): 12—13

徐獻明, 張志勇, 曹 昆, 2014. 小黃魚幼魚人工培育技術.水產養殖, 35(8): 22—24

董在杰, 梁政遠, 明俊超等, 2010. 尼羅羅非魚體重與體維可量性狀之間的關系. 廣東海洋大學學報, 30(1): 32—38

謝立峰, 付賢康, 2006. 小黃魚親體培育技術. 中國水產, (1):50—51

樓允東, 1999. 魚類育種學. 北京: 中國農業出版社, 3—5

Ahmed M, Abbas G, 2000. Growth parameters of the finfish and shellfish juvenile in the tidal waters of Bhanbhore, Korangi Creek and Miani Hor Lagoon. Pakistan Journal of Zoology,32(1): 21—26

Chen D G, Liu Q, Zeng X Q et al, 1997. Catch composition and seasonal variation of setnet fisheries in the Yellow and Bohai Seas. Fisheries Research, 32(1): 61—68

Efroymson M A, 1960. Mathematical Methods for Digital Computers. New York: Wiley

Ezekiel M, 1941. Methods of Correlation Analysis. 2nd edn. New York: Wiley

Froese R, Pauly D, 2014. FishBase: world wide web electronic publication. http://www.fishbase.org

Jin X S, Tang Q S, 1996. Changes in fish species diversity and dominant species composition in the Yellow Sea. Fisheries Research, 26(3—4): 337—352

Land K C, 1969. Principles of path analysis. Sociological Methodology, 1: 3—37

Nguyen N H, Ponzoni R W, Abu-Bakar K R et al, 2010.Correlated response in fillet weight and yield to selection for increased harvest weight in genetically improved farmed tilapia (GIFT strain), Oreochromis niloticus. Aquaculture,305(1—4): 1—5

Tr?ng T Q, Han A M, Arendonk J A M V et al, 2013. Heritability and genotype by environment interaction estimates for harvest weight, growth rate, and shape of Nile tilapia(Oreochromis niloticus) grown in river cage and VAC in Vietnam. Aquaculture, 384—387: 119—127

Wang L, Liu S F, Zhuang Z M et al, 2015. Mixed-stock analysis of small yellow croaker Larimichthys polyactis providing implications for stock conservation and management.Fisheries Research, 161: 86—92