鋼彈簧支座阻尼對被動式減振浮置板軌道低頻振動控制的影響

張龍慶　蔡成標　王開云　朱勝陽　肖　威

(西南交通大學牽引動力國家重點實驗室　四川成都　610031)

?

鋼彈簧支座阻尼對被動式減振浮置板軌道低頻振動控制的影響

張龍慶蔡成標王開云朱勝陽肖威

(西南交通大學牽引動力國家重點實驗室四川成都610031)

摘要：針對城市軌道交通用浮置板軌道低頻振動控制問題，基于動力吸振器定點理論、模態解析原理及車輛-軌道耦合動力學理論，充分考慮浮置板下鋼彈簧支座阻尼的影響，采用車輛-被動減振浮置板軌道動力學模型，研究被動式減振浮置板軌道低頻振動控制問題。以加速度三分之一倍頻程及插入損失為評判標準，定量分析了鋼彈簧支座阻尼對被動式減振浮置板軌道低頻振動控制的影響，為被動式減振浮置板低頻振動控制提供參考依據。

關鍵詞：動力吸振器浮置板軌道車輛-軌道耦合動力學低頻振動鋼彈簧支座阻尼

近年來城市軌道交通發展迅速，由此引起的環境振動與噪聲污染問題成為國內外專家學者們的研究熱點[1-3]。其中，列車動荷載引起的低頻振動由于其傳播距離遠、衰減緩慢等特點，對沿線建筑物內的精密儀器甚至人體產生了不良影響。因此，在研究各類減振措施的同時，有必要對它們的低頻減振特性進行相關研究。我國《地鐵設計規范》規定，城市軌道交通特殊減振路段宜采用鋼彈簧浮置板道床進行振動控制。但研究結果表明，浮置板軌道在其固有頻率以上具有良好的隔振性能，當激勵荷載頻率小于浮置板自身固有頻率時，浮置板軌道難以起到理想的隔振效果[4]。所以，研究浮置板低頻振動控制尤其是浮置板自身固有頻率附近的低頻振動控制顯得尤為重要。

降低軌道系統剛度或者增加軌道系統質量來降低軌道結構自身固有頻率是進一步實現軌道結構低頻振動控制的傳統方法。低頻浮置板軌道專利[5]通過增加軌道板的質量來降低系統的固有頻率，但是這種方法受到建設成本以及鐵路限界所限，難以實現廣泛應用；與此同時，通過彈性軌枕等減振元件來降低軌道系統剛度將導致軌道系統振動位移大幅增大，嚴重威脅列車運行的安全性。文獻[6-7]設計了一種應用動力吸振器進行低頻減振的被動式減振浮置板軌道。這種軌道結構能夠有效控制鋼彈簧浮置板軌道結構自身共振引起的低頻振動。對于鋼彈簧浮置板軌道下部鋼彈簧支座阻尼對被動式減振浮置板軌道低頻振動控制的影響，目前相關研究并不多見。本文運用動力吸振器相關設計理論[8-11]以及車輛-軌道耦合動力學理論[12]，采用有限單元法，分析了浮置板下鋼彈簧支座阻尼對被動式減振浮置板軌道相關設計參數及減振效果的影響。

1被動式減振浮置板軌道結構

被動式減振浮置板軌道結構如圖1所示。通過在傳統浮置板軌道主板上附加一個由彈簧、阻尼及附加質量子結構組成的動力減振系統，利用附加質量子結構和彈簧的參數合理匹配，將浮置板主板的低頻振動能量吸收并加以增幅，通過動力減振系統中的阻尼元件消耗部分低頻振動能量，實現浮置板主板的低頻振動控制。需要注意的是，本文的被動式減振浮置板軌道主要通過動力減振系統抑制浮置板軌道一階模態的低頻振動。

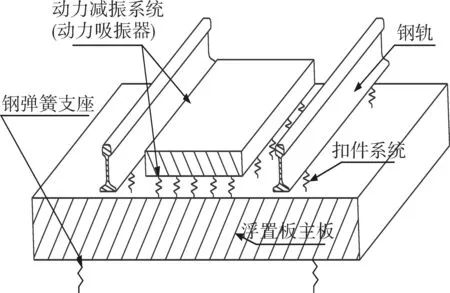
圖1　被動式減振浮置板軌道

2被動式減振浮置板軌道設計方法

從結構本身屬性考慮，浮置板軌道為一連續系統。對該系統進行制振設計時，首先利用模態解析原理[10]，通過非耦合化處理將連續系統離散為多個單自由度系統的集合，然后通過單自由度系統制振方法進行被動式減振浮置板軌道動力減振系統設計。通過模態解析原理得到的浮置板軌道系統模態剛度和模態質量沒有實際物理含義，需要進一步變換成具有實際物理意義的參量。

由模態質量定義知：

M=XT·m·X

(1)

式中,X為系統模態振型；XT為系統模態振型轉置；m為物理質量；M為系統模態質量。

由動能定理可得：

(2)

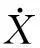
引進單位矩陣I=XXT，代入公式(2)變為：

(3)

將系統模態質量公式(1)代入公式(3)，得：

(4)

(5)

整理，得：

(6)

其中ωT和ω都是對角矩陣，故系統模態質量可表示為：

(7)

通過獲得浮置板軌道第i階模態的系統總動能Ti以及系統第i階振動角頻率ωi，便可通過公式(7)得到系統第i階的模態質量Mi。由此可得系統第i階模態剛度：

(8)

基于上述等價質量識別法得到浮置板軌道系統第i階模態的等效剛度和等效質量后，可采用單自由度系統動力吸振器的設計方法，獲取被動式減振浮置板軌道附加動力減振系統的最優參數。根據文獻[10]中的定點理論最優參數公式，可得浮置板第i階模態對應的動力減振系統的最優質量、最優阻尼、最優剛度3個最優參數設計公式。

最優質量：

mi=μiMi

(9)

最優阻尼：

(10)

最優剛度：

(11)

根據上述最優參數確定公式，結合給定質量比μi，便可得到對應于浮置板第i階模態的附加動力減振系統的最優設計參數。值得注意的是，這里系統第i階模態阻尼Ci不能直接得到，可根據動力吸振器最優同調[10]原理求出。

3附加動力減振系統最優參數確定

采用有限元軟件ANSYS，建立了傳統的鋼彈簧浮置板軌道有限元模型，如圖2所示。其中，鋼軌采用Beam188單元模擬，軌道板采用Solid45單元模擬；板縱向兩端面施加對稱約束模擬板間的剪力鉸；鋼彈簧支座采用Combin14彈簧阻尼單元模擬，扣件系統同樣采用Combin14彈簧阻尼單元模擬。軌道板板長為4 m，寬為3 m，鋼彈簧支座間距為1.2 m，扣件系統間距取0.6 m。扣件垂向剛度和鋼彈簧垂向剛度分別取30 kN/mm和7.5 kN/mm。

圖2　浮置板有限元模型

圖3為采用有限元軟件ANSYS獲取的傳統浮置板軌道第一階平動模態，第一階固有頻率為13.089 Hz。通過ANSYS計算得到傳統浮置板軌道一階模態的總動能T1，便可利用公式(7)-(11)及質量比μ1得到被動式減振浮置板軌道動力減振系統的最優設計參數。計算中，被動減振浮置板動力減振系統質量比取0.1。計算得到不同鋼彈簧支座阻尼比Z(0.01，0.02，0.04和0.08)下附加動力減振系統最優設計參數如表1所示。圖4給出了附有一階模態動力減振系統的被動式減振浮置板軌道有限元模型。

圖3　浮置板軌道一階模態

圖4　被動減振浮置板軌道模型

鋼彈簧阻尼比最優質量/kg最優剛度/kN·mm-1最優阻尼/(kN·s·m-1)0.01956.325.0228.520.02956.324.9528.520.04956.323.2228.520.08956.321.3328.52

4被動式減振浮置板軌道減振性能分析

4.1浮置板主板振動加速度和鋼彈簧支點反力分析

基于車輛-軌道耦合動力學理論，通過Matlab軟件編程計算得到軌道不平順作用下的輪軌相互作用力。其中，車輛運行速度取80 km/h，采用地鐵標準B2型車，車輛主要參數參見文獻[6]。車輛模型采用翟婉明院士提出的新型顯示積分法進行求解。軌道不平順激勵源采用美國五級軌道譜，波長范圍取1～30 m。

將上述方法計算得到的輪軌相互作用力施加到軌道結構上，對列車動荷載作用下被動式減振浮置板軌道的吸振特性進行分析，計算得到了傳統浮置板主板和被動式減振浮置板主板的加速度和鋼彈簧支點反力。不同浮置板鋼彈簧支座阻尼比條件下，浮置板主板的加速度和浮置板下鋼彈簧支點反力僅是幅值有所不同，變化規律基本一致。因此，這里只給出了鋼彈簧支座阻尼比取0.01時的計算結果，如圖5、圖6所示。圖中實線表示被動減振浮置板軌道主板加速度和鋼彈簧支點反力的計算結果，虛線表示傳統浮置板軌道主板加速度和鋼彈簧支點反力的計算結果。

圖5　浮置板振動加速度

由圖5(a)可知，列車動荷載作用下，被動式減振浮置板軌道主板振動加速度比傳統浮置板軌道主板振動加速度的峰值減小，加速度衰減速度也明顯加快。由5(b)可知，列車動荷載作用下，傳統浮置板主板的振動加速度在浮置板軌道一階固有頻率13 Hz附近出現明顯峰值，而被動式減振浮置板軌道主板加速度在浮置板軌道一階固有頻率處峰值顯著減小。表明被動式減振浮置板軌道有效抑制了浮置板軌道一階共振頻率處的低頻振動。

圖6　浮置板鋼彈簧支點反力

由圖6(a)可知，被動式減振浮置板軌道下最大鋼彈簧支點反力較傳統浮置板軌道下最大鋼彈簧支點反力略有減小，但差別不大；圖中虛線方框中計算結果還可以看出，相比于傳統浮置板，車輛第二、三位輪對經過鋼彈簧支座時，被動式減振浮置板鋼彈簧支點反力明顯有所減小。由圖6(b)可知，列車動荷載作用下，傳統浮置板軌道下鋼彈簧支點反力在浮置板軌道一階固有頻率13 Hz附近也有明顯峰值，被動式減振浮置板軌道下鋼彈簧支點反力在浮置板軌道一階固有頻率13 Hz處峰值也明顯減小。表明被動式減振浮置板能夠有效抑制浮置板軌道一階共振頻率處的低頻振動向附近建筑物傳遞。

4.2鋼彈簧支座阻尼對被動式減振浮置板吸振效果的影響

圖7為鋼彈簧支座阻尼比取0.01時的傳統浮置板較被動減振浮置板振動加速度級對比曲線。由圖7可知，在10～16 Hz頻率范圍內，被動式減振浮置板軌道能夠有效降低浮置板主板的振動加速度級，并且在浮置板軌道結構一階固有頻率13 Hz處浮置板主板加速度級衰減最為明顯。

圖7　加速度振動級1/3倍頻程

圖8為不同浮置板鋼彈簧支座阻尼比條件下，傳統減振浮置板軌道較被動減振浮置板軌道振動加速度級插入損失。從圖8可以看出，插入損失隨著鋼彈簧阻尼比的增大而減小。表明浮置板鋼彈簧支座阻尼比越小，被動式減振浮置板減振效果越明顯。

表2給出了浮置板不同鋼彈簧支座阻尼比條件下傳統浮置板軌道較被動式減振浮置板軌道振動加速度級插入損失最大值。由表2可以看出，鋼彈簧支座阻尼比取0.01時，插入損失最大，為10.68 dB；鋼彈簧支座阻尼比取0.08時，插入損失最小，為1.48 dB。

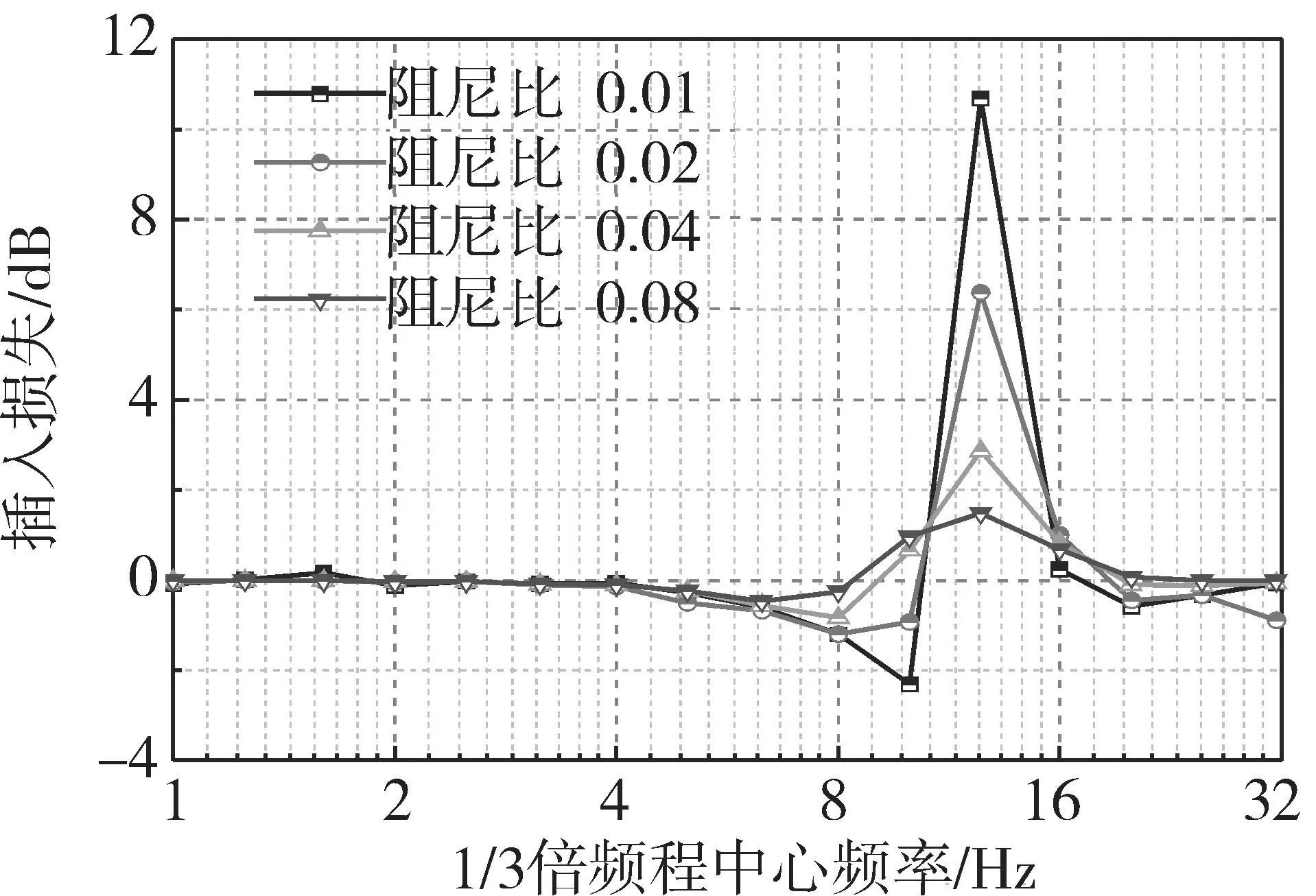
圖8　不同鋼彈簧阻尼比下插入損失

阻尼比0.010.020.030.04最大插入損失/dB10.686.382.861.48

5結論

針對城市軌道交通引起的浮置板軌道結構低頻共振放大現象，基于動力吸振器相關設計方法及車輛-軌道耦合動力學理論，研究了鋼彈簧支座阻尼對于被動式減振浮置板低頻振動控制的影響。通過被動式減振浮置板軌道最優設計方法，得到了浮置板附加動力減振系統最優設計參數。利用有限元軟件ANSYS在列車動荷載作用條件下對浮置板軌道進行動力學分析，可得到以下結論：(1)被動式減振浮置板軌道能夠有效地抑制浮置板自身共振頻率及其附近頻段的低頻振動。(2)被動式減振浮置板軌道鋼彈簧支座阻尼比取為0.01時，被動式減振浮置板軌道較傳統浮置板軌道可使13 Hz附近的低頻振動降低，有效控制浮置板自身共振低頻振動向周圍基礎及建筑物的傳遞。(3)隨著被動式浮置板軌道鋼彈簧支座的阻尼逐漸減小，浮置板主板振動加速度的插入損失越大，被動減振浮置板軌道減振效果越明顯。

參考文獻

[1]李俊嶺. 地鐵鋼彈簧浮置板軌道對環境振動的影響分析[D]. 成都：西南交通大學, 2011.

[2]劉衛豐, 劉維寧, 袁揚, 等. 地鐵列車與道路車輛運行對環境的振動影響現場測試與分析[J]. 鐵道學報， 2013, 35(5) : 81-84.

[3]孫曉靜,劉維寧,郭建平,等. 地鐵列車振動對精密儀器和設備的影響及減振措施[J]. 中國安全科學學報, 2005,15(11):78-81.

[4]GUPTA S, DEGRANDE G. Modelling of continuous and discontinuous floating slab tracks in a tunnel using a periodic approach[J]. Journal of Sound and Vibration, 2010, 329(8):1101-1125.

[5]北京市市政工程設計研究總院. 低頻浮置板軌道: 中國, CN 102535260 B[P]. 2014-04-23.

[6]楊吉忠, 顏華, 蔡成標. 城市軌道交通低頻減振軌道結構研究[J]. 鐵道學報, 2015.

[7]楊吉忠, 顏華, 林紅松, 等. 被動式動力吸振軌道板: 中國, 203546523[P]. 2014-04-16.

[8]劉耀宗, 郁殿龍, 趙宏剛, 等. 被動式動力吸振技術研究進展[J]. 機械工程學報, 2007,43(3):14-21.

[9]盛美萍, 王敏慶, 孫進才. 噪聲與振動控制技術基礎[M]. 北京: 科學出版社, 2007.

[10] 背戶一登. 動力吸振器及其應用[M]. 北京: 機械工業出版社, 2013.

[11] DEN HARTOG J P. Mechanical Vibrations[M]. (3rd Edition). New York: McGraw-Hill, 1947.

[12] 翟婉明. 車輛-軌道耦合動力學[M], 第三版. 北京: 科學出版社, 2007.

Influence of Damping Coefficient of Steel Spring Bearings on Passive

Damping Floating Slab Track in Low Frequency Vibration Control

ZHANG Long-qing,CAI Cheng-biao,WANG Kai-yun,ZHU Sheng-yang,XIAO Wei

(TractionPowerStateKeyLaboratory,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China)

Abstract:Taking the problem of low-frequency vibration control of the floating slab track, based on the fixed-point theory, modal analysis principle and the vehicle-track coupled dynamics, and fully considering the effect of damping coefficient of steel spring bearings, the vehicle-passive dynamic damping slab track(PDDFST) coupled dynamic model is used to study low-frequency vibration control of PDDFST. Taking the one third octave frequency band and insertion loss of acceleration level as the evaluation criterion, quantitative analysis of the influence of damping coefficients of steel spring bearings on low-frequency vibration control of PDDFST. Research results can provide a reference for low-frequency vibration control of floating slabs.

Key words:The dynamic absorber;The floating slab track;Vehicle-track coupled dynamics;Low-frequency vibration;Damping coefficient of steel spring bearings

中圖分類號：U213.2+41

文獻標志碼：A

文章編號：1671-8755(2015)04-0033-05

作者簡介:張龍慶(1989—)，男，碩士研究生。E-mial:695591306@qq.com

收稿日期：2015-07-01