帶U形阻尼器的鋼框架梁柱節點滯回性能分析

楊應華，徐增武，楊 超

(西安建筑科技大學土木工程學院，陜西 西安710055)

梁柱節點是鋼框架中關鍵的部件，它保證了梁柱協同工作，并使結構形成了整體．鋼框架結構梁柱的典型連接是梁腹板與柱通過節點板以及高強螺栓連接，而梁翼緣與柱翼緣通過焊縫連接的栓焊混合連接．然而這種典型梁柱栓焊混合連接方式容易非預期脆性破壞[1-3],1994年的北嶺地震和 1995年的阪神地震震害中大部分鋼框架梁柱節點的破壞既是這種破壞．為了克服這一弊端，國內外學者對傳統的梁柱栓焊混合連接方式提出了多種改進措施，主要有：削弱梁翼緣；改進焊接細節；對連接部位翼緣進行加強；采用高強螺栓進行連接等[4]．這些改進措施雖然改善了節點的抗震性能，但這些措施都是通過將鋼梁塑性鉸外移來達到耗能的目的，因此，節點一旦破壞將很難修復．

為便于梁柱節點的震后修復，近幾年國內外學者基于被動控制思想提出了將金屬阻尼器設置在梁-柱節點處以達到提高節點耗能能力，并保護結構主體不受損壞的目的[5-7]．文獻[6]提出的梁-柱弱軸連接節點，將金屬阻尼器設置在梁下翼緣處，經試驗驗證該節點具有飽滿的滯回環，穩定的滯回性能，且塑性變形主要集中在阻尼器上，而梁柱等主體結構未出現破壞，達到預期效果．然而，這種節點能承受的剪力和彎矩很小且僅適用于梁柱弱軸方向的連接．為此，本文第一、二作者提出了一種承載力更大且適用于梁柱強軸連接的帶 U形阻尼器梁柱節點[8]．下文擬通過有限元軟件 ABAQUS對這種節點進行分析，以考察其滯回性能．

1 節點設計

1.1 節點構造

所提出帶U形阻尼器節點構造如圖1所示[8]，柱翼緣與牛腿焊接，牛腿的另一端上翼緣通過高強螺栓及連接板 1、2與梁上翼緣相連；腹板處通過高強螺栓及一對U形阻尼器與梁的腹板相連；下翼緣處通過高強螺栓及三個 U形阻尼器與梁的下翼緣相連．連接設計中，通過調整各部件的尺寸使節點的轉動中心位于梁上翼緣，腹板處的U形阻尼器來傳遞剪力，腹板處的阻尼器承擔小部彎矩，上翼緣連接板和下翼緣處的 U形阻尼器傳遞大部分彎矩(如圖2所示)．圖3為U形阻尼器及其尺寸．

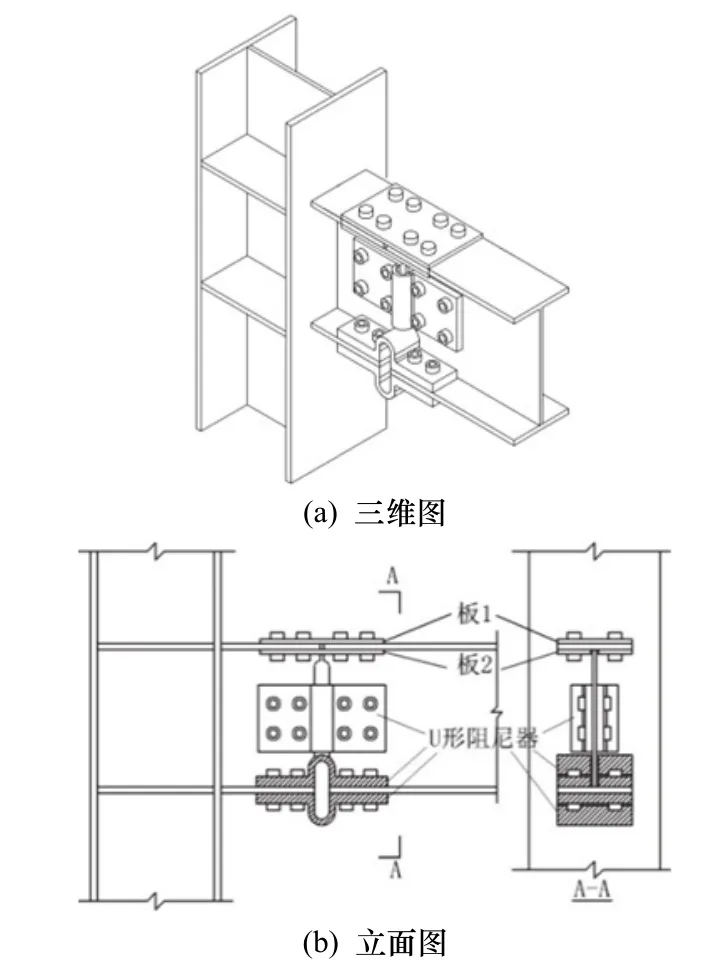
圖1 帶U形阻尼器節點構造Fig.1 Connection with U-shaped dampers

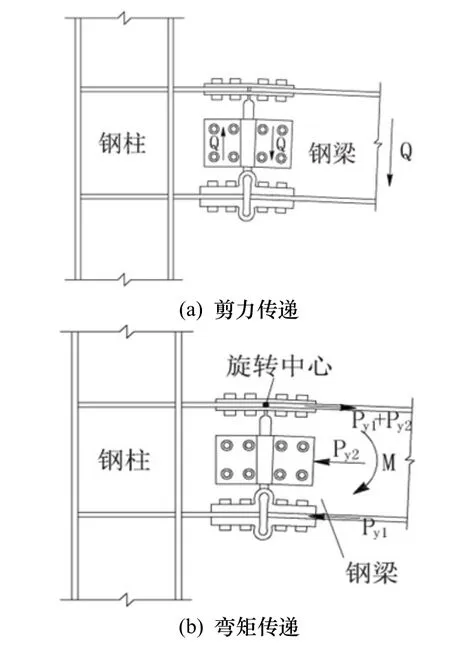
圖2 荷載傳遞圖Fig.2 diagram of load transfer

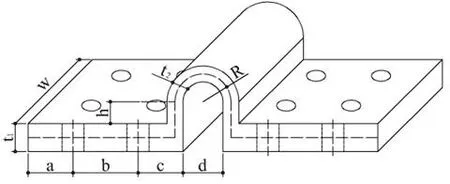
圖3 U形阻尼器Fig.3 U-shaped dampers

1.2 連接部件

梁上翼緣高強螺栓個數應保證高強螺栓抗剪承載力之和大于梁上翼緣截面軸向屈服荷載，即

其中：n為拼接處一側螺栓數量，Ps為高強螺栓預緊力，μ為連接平板與梁上翼緣之間的摩擦系數，fy為梁上翼的屈服強度，tf為梁上翼緣厚度，b為梁上翼緣寬度．

梁上翼緣拼接板截面面積之和應大于梁上翼緣截面面積，拼接板長度應根據螺栓直徑和布置方式確定．

梁腹板上高強螺栓個數應保證高強螺栓抗剪承載力之和大于梁腹板的抗剪承載力，即

其中n為阻尼器一側螺栓數量，Ps為高強螺栓預緊力，μ為連接平板與梁上翼緣之間的摩擦系數，fv為梁腹板的剪切屈服強度，hw為梁腹板的高度，tw為梁腹板厚度．

上翼緣及腹板處的高強螺栓均應對稱布置，并應滿足螺栓間距要求[9]．

腹板處一對U形阻尼器U形段橫截面面積之和應不小于梁腹板截面面積，即

其中t2w為阻尼器U形段厚度，ww為腹板處U形阻尼器寬度，tw及hw分別為梁腹板的厚度和高度．

由圖2(b)可知，腹板處及下翼緣處阻尼器所能承受的沿鋼梁長度方向最大軸力之和應小于梁上翼緣的屈服時的軸力，即

同時，為了保證鋼梁不發生破壞，梁腹板及下翼緣處阻尼器所能承受最大的彎矩之和應小于梁的塑性彎矩Mp，即

其中：h1為節點轉動中心到下翼緣處阻尼器合力作用點的距離，h2為轉動中心到腹板處阻尼器合力作用點距離，h2為h1的二分之一．對 H形鋼梁，若式(4a)滿足，則式(4b)也滿足．

腹板及下翼緣處阻尼器所能承受最大的彎矩應大于梁的設計彎矩Md，才能保證節點正常使用及多遇地震下的抗彎能力，即：

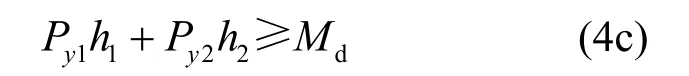
根據現行鋼結構設計[9]，H形鋼梁翼緣通常承擔約超過其 80%的塑性彎矩，H形鋼梁的設計彎矩Md最大約為其塑性彎矩Mp的62%，由式(4a、c)可得：

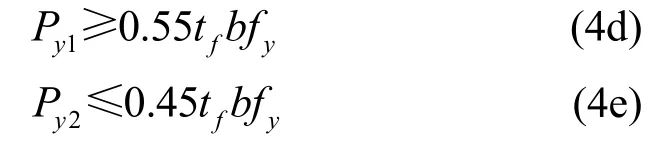
其中：Py1為下翼緣處阻尼器的抗拉(壓)屈服荷載，Py2為腹板處阻尼器的抗拉(壓)屈服荷載．

U 形阻尼器抗拉(壓)屈服荷載可按下式計算[10]，式中阻尼器的截面參數詳圖3所示．

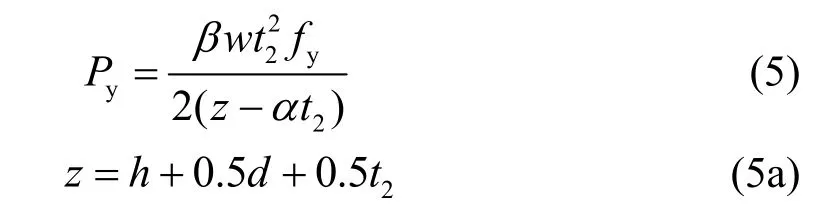
其中：β為矩形截面寬厚比對截面塑性彎矩提高系數(表1)，w為阻尼器寬度；α為阻尼器平直段對U形段約束形成的塑性鉸偏移影響系數，可近似取為0.14(阻尼器平直段厚度不小于U形截面段厚度1.5倍時該系數成立)．下翼緣螺栓個數可按下式計算：

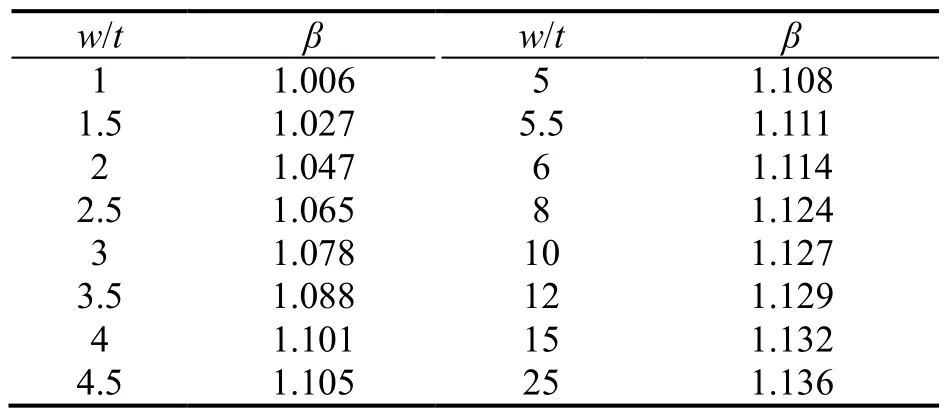
表1 矩形截面塑性彎矩提高系數Tab.1 plastic moment increase coefficients for rectangular section

為實現易修復的目的，節點設計時需保證U形阻尼器達到極限承載力之前，梁柱基本保持在彈性范圍內；同時應減少Py2而增大Py1．

2 有限元模型

2.1 節點尺寸

柱選用 H 型鋼 350×350 ×12×19，梁與牛腿選用H型鋼 400×200×10×16，材料均選用 Q235鋼材．為保證梁柱節點域在節點破壞前不發生屈服，節點域柱腹板厚度根據文獻[9]中節點域抗剪強度計算公式進行驗算．這里梁彎矩偏安全地按全截面塑性彎矩取值．可以算得節點域厚度不得小于15.7 mm，因此需對節點域進行加強，將節點域加厚至16 mm．

根據2中的步驟和要求選用梁上翼緣連接板為－14×200×370 及-14×90×370，上翼緣螺栓采用 10.9級M24高強螺栓，下翼緣及腹板處采用10.9級M22高強螺栓，節點尺寸如圖4所示．

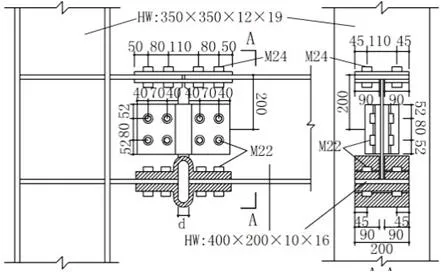
圖4 計算節點Fig.4 Selected connection

按圖4所示節點尺寸選定各U形阻尼器的尺寸作為基準節點JD1，其阻尼器尺寸如表1所示，相應的屈服彎矩理論值為167.04 kN．

表2 帶U形阻尼器節點模型參數Tab.2 Parameters of models for connectionsof U-shaped dampers

在JD1基準節點的基礎上，另外又構建了9個節點共分為四組．四組節點分別對阻尼器U形截面段厚度、高度、半徑及阻尼器平直段厚度進行了變化，表2同時列出了其他各節點U形阻尼器的相關參數，其中相對于JD1改變的參數以下劃線的方式在表中標出，其中A組(JD2、3)改變翼緣處U形截面厚度；B組(JD4、5)改變翼緣處U形截面直段尺寸；C組(JD6、7)改變翼緣、腹板處U形段直徑；D組(JD8、9、10)改變翼緣處阻尼器平板截面厚度．

2.2 分析模型

取一梁柱邊節點，如圖5所示，其中柱高為2 000 mm，其中牛腿長250 mm，梁長2 000 mm．集中荷載施加在距梁端拼接中心1.925 m處，以豎直向上為負，豎直向下為正，由于節點的轉角變形主要發生在牛腿與梁的拼接處，θ取為梁相對于牛腿拼接點中心轉角，該拼接點處彎矩為：M=1.925P．

有限元模型將柱頂部和底部全部自由度約束住，同時將框架梁的平面外自由度也約束住，以避免梁平面外失穩對分析結構造成影響，且為了簡化分析，模型并未考慮P-δ效應對節點的影響．模型未考慮焊接殘余應力和初始幾何缺陷對節點的影響．

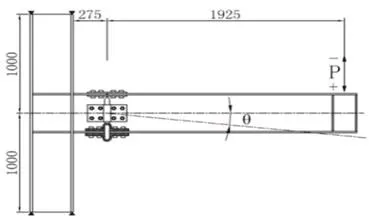
圖5 計算模型Fig.5 Joint model

各節點模型均采用實體單元建模，選擇的單元類型為8節點六面體單元(C3D8R)，該單元適合接觸分析和彈塑性分析，模型根據結構應力梯度進行不同密度的網格劃分，在應力梯度較大處(如 U形阻尼器、螺栓、連接板)采用密度較大的網格，帶U形阻尼器易修復梁柱節點的網格劃分如圖6所示．

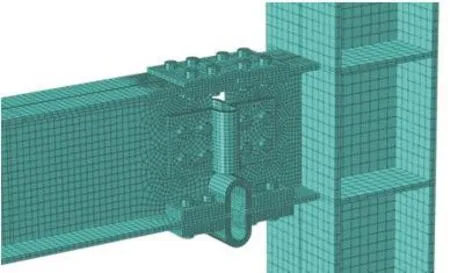
圖6 帶U阻尼器節點的網格劃分Fig.6 FE mesh of a connection with U-shaped damper s

2.3 本構模型

鋼材的本構模型采用雙線性隨動強化模型，該模型已考慮了包辛格效應，在循環荷載作用下無剛度退化，模擬的鋼材本構參數詳見表3．

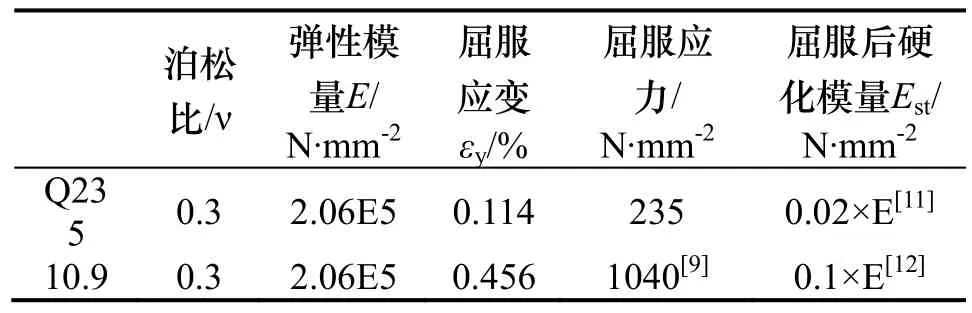
表3 鋼材本構關系Tab.3 Constitutive relation for steel

2.4 接觸設置

有限元模型考慮螺栓孔壁與螺栓桿之間的接觸關系，接觸屬性中的法向作用按默認的“硬接觸”，并忽略孔壁與螺桿之間的摩擦．為了簡化計算，牛腿與鋼柱的連接通過綁定的形式連接在一起，螺帽也通過綁定的形式與各連接件組合．各連接構件與牛腿和鋼梁之間的接觸對的法向作用同樣采用默認的“硬接觸”，而切向設有抗滑移系數，其取值為0.45[9]．

2.5 加載制度及約束情況

采用了兩種加載方式，分別為單向加載方式和循環加載方式．單向加載方式分析節點破壞模式，ECCS[13]的循環加載制度分析帶U形阻尼器節點的滯回性能，用轉角位移控制．位移幅值分別為θy/4(1周)，θy/2(1周)，3θy/4(1周)，θy(1周)，2θy(3周)，3θy(3周)，4θy(3周)……如圖5,6所示，其中θy是節點發生屈服的轉角位移，θy及My按文獻[14]所提出的方法選取，如圖7所示，其中：K1為初始轉動剛度；K2為屈服后轉角剛度；θy為屈服轉角；θu為極限轉角．理想的雙線性曲線確定的方法為：在非線性轉角-彎矩曲線下面的面積與理想的雙線性轉角-彎矩曲線下面的面積接近．在滯回分析前，先進行單調靜力分析以確定上述相應參數．

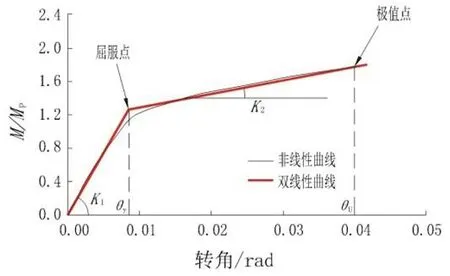
圖7 θy確定方法Fig.7 Method of determing θy

當曲線發生下列現象之一時，可判斷為構件達到極限承載力：

(1) 本級循環中的最大荷載比前一級循環中的最大荷載小；(2) 滯回曲線出現下降段，即斜率為負；(3) 若曲線未出現下降段，可按梁轉角達到0.04時所對應的荷載作為極限荷載[15]．

2.6 模型驗證

以上述ABAQUS模型模擬文[6]中的SP1～SP4試件．試件材料屬性、幾何尺寸、荷載條件以及邊界條件均按照文獻[6]模擬，將模擬得出的節點的滯回曲線與文獻中實驗得出的節點滯回曲線進行對比，如圖8所示．由圖8(a)可以看出：有限元模擬結果和試驗結果有較高的吻合度，兩者滯回曲線趨勢相同．因此，前述ABAQUS有限元模型具有較高的精度，可用于后文模型試件的分析．

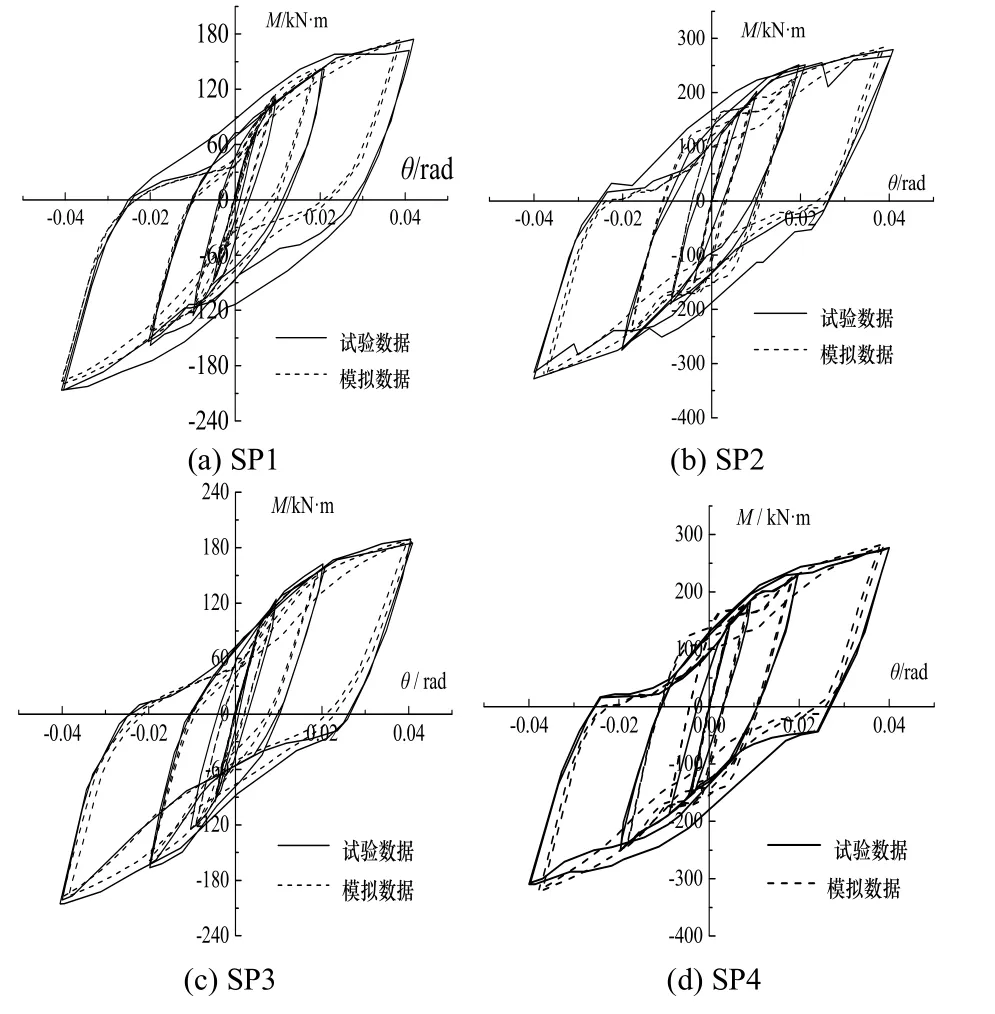
圖8 有限元模擬曲線與試驗曲線對比Fig.8 Comparison between of finite element simulation results and test results

3 有限元計算結果

3.1 破壞模式

圖9為JD1在單向加載過程中各階段的應力云圖．從圖中可以看出，屈服現象最先出現在鋼梁下翼緣處的U形阻尼器，隨后出現在腹板處的U形阻尼器．圖9(c)為JD1在轉角位移達到0.009 rad時的應力云圖，此時有有限元計算得出的節點彎矩為178.1 kN，而JD1屈服彎矩理論值為166.3 kN，說明節點已進入屈服階段．從圖中可以看出，JD1發生屈服時，梁、柱及牛腿仍處于彈性階段，僅在梁下翼緣處的阻尼器發生了全截面塑性屈服．圖9(d)為JD1在極限荷載下的應力云圖，此時塑性應力仍主要集中在U形阻尼器上，梁、柱及牛腿雖出現局部屈服現象但基本上仍處在彈性階段．

帶U形阻尼器梁柱節點中最先破壞的構件為U形阻尼器，而梁、柱及牛腿始終處于彈性階段，在節點破壞后只需更換新的 U形阻尼器便可達到修復的目的．

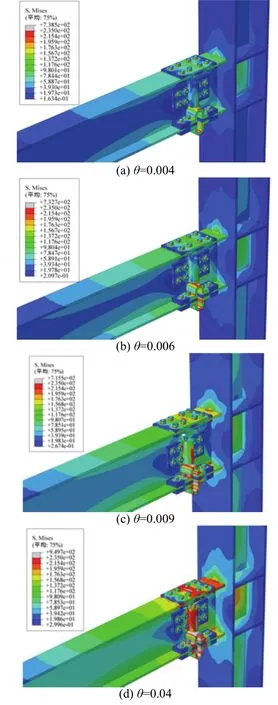
圖9 JD1應力云圖Fig.9 Stress contours of JD1

3.2 滯回分析

節點在循環荷載作用下，每經歷一次循環，加載時吸收能量，卸載時釋放能量，二者之差即節點在一次循環中消耗的能量，也就是一個滯回環所包圍的面積[16]．

圖10為各節點的滯回曲線，從圖中可以看出各節點在加載初期，彎矩與轉角呈線彈性，且滯回環面積較小，耗能小；當節點進入彈塑性階段時，節點彎矩增幅減緩，滯回環面積逐漸增大，耗能增加．通過圖10可以看出，除了JD-8以外，其余節點均表現出滯回環飽滿，滯回曲線穩定的性能．由JD-3、JD-4和JD-6的滯回曲線可以看出隨著鋼梁下翼緣處阻尼器U形段截面高度的減小、厚度的增加以及半徑的減小，節點在較小的轉角變形下將發生螺栓的滑移，滑移量在1.4 mm左右，這導致節點滯回曲線發生輕微捏縮現象．

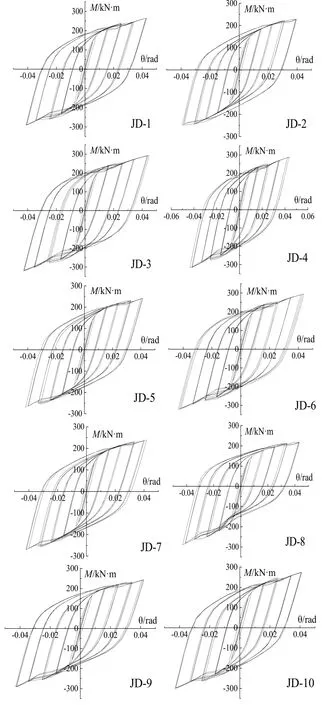
圖10 滯回曲線Fig.10 Hysteretic loops

由JD-8的滯回曲線可知，當U形阻尼器平直段厚度和U形段厚度相同時，滯回曲線將會出現明顯不對稱的捏縮現象，由JD-1、JD-9及JD-10的滯回曲線可知，隨著U形阻尼器的平直段厚度的增加，節點的滯回曲線趨于對稱飽滿，且沒有明顯捏縮現象．JD-1、JD-9及JD-10的滯回曲線之所以對稱均勻是因為當U形阻尼器平直段比U形截面段厚時，不論正向加載還是負向加載，阻尼器首先發生屈服的位置是U形截面段，如圖11所示，這使節點的正負向加載的屈服荷載區別不大．當U形阻尼器平直段厚度不大于U形段截面厚度時，在正向荷載作用下，阻尼器的U形段只在頂部和平直段產生塑性鉸，如圖12(a)所示，平直段先于U形截面段底部出現塑性鉸將大幅降低節點的屈服荷載；而在負向荷載作用下由于阻尼器平直段的彎曲變形受到梁翼緣的限制，阻尼器的塑性鉸仍只發生在阻尼器U形段，如圖12(b)所示，這導致了阻尼器負向加載下的屈服荷載明顯大于正向加載下的屈服荷載，造成了JD8的滯回曲線表現出不對稱性且有明顯的捏縮現象．因此，在設計這種節點時，U形阻尼器平直段的厚度應比U形段截面厚度大，這樣才能保證節點滯回曲線飽滿對稱．不能通過一塊鋼板軋制成U形阻尼器，增加了阻尼器設計的工藝難度也是這種構造的缺點之一．

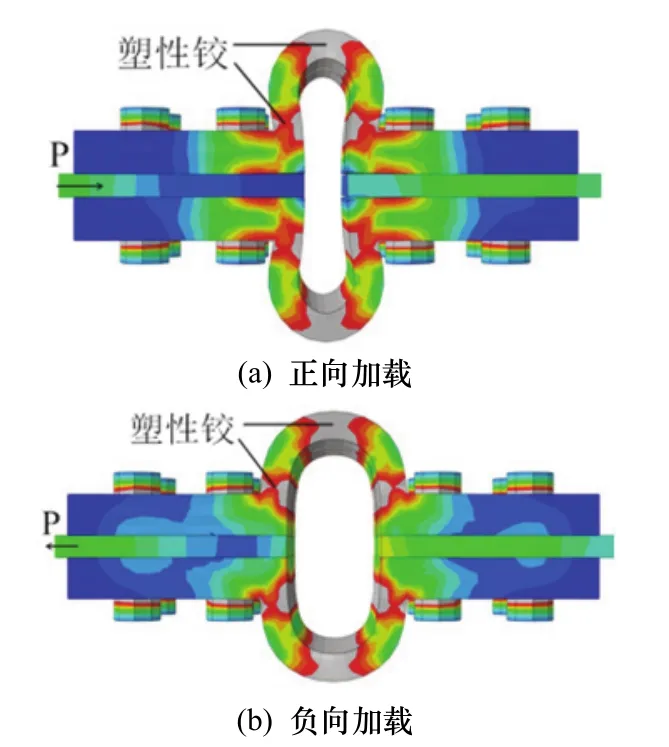
圖11 JD1的U形阻尼器應力云圖Fig.11 Stress contours of U shaped damper of JD1

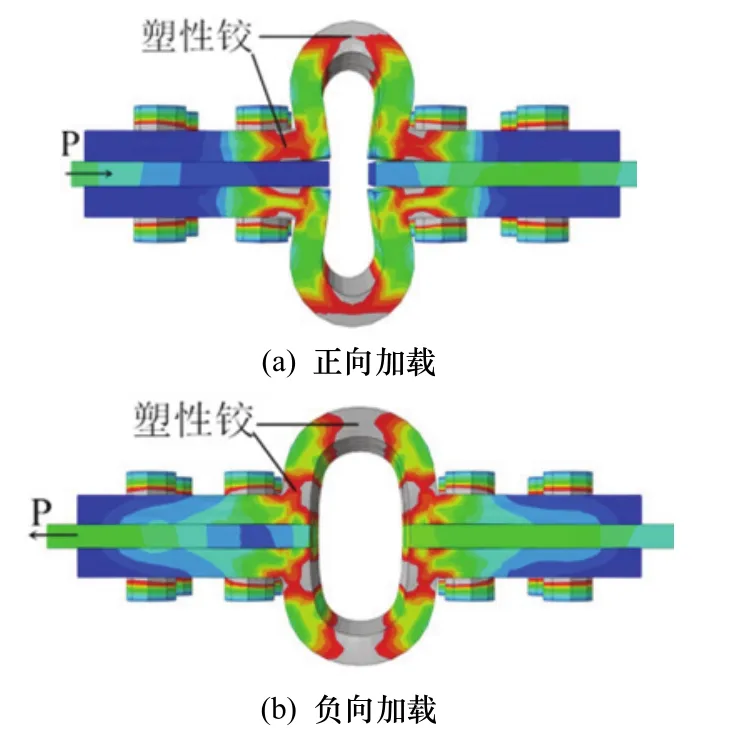
圖12 JD8的U形阻尼器應力云圖Fig.12 Stress contour of U shaped damper of JD8

3.3 骨架曲線

圖13為節點的骨架曲線，表4為各節點在不同加載方向下的屈服荷載．

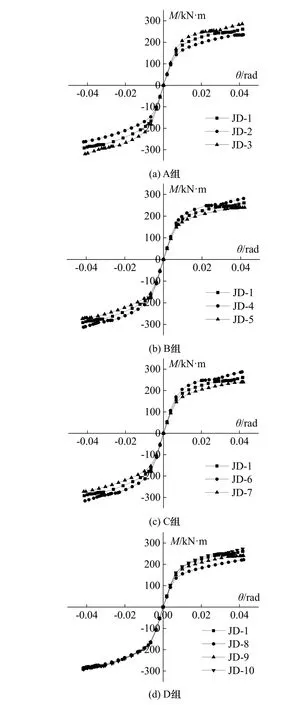
圖13 骨架曲線Fig.13 Skeleton curves

由圖13a～13c及表4可知，隨著阻尼器U形段直段高度的減小、截面厚度的增加以及半徑的減小，節點的屈服荷載均提高．

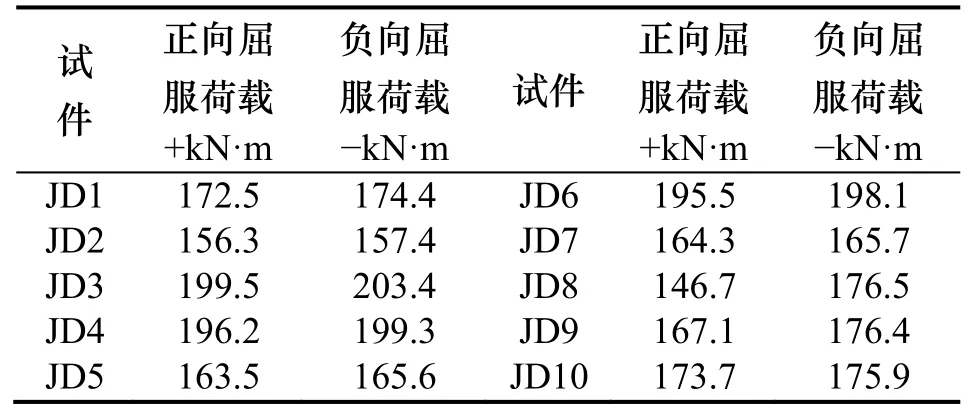
表4 各節點屈服荷載Table.4 The yield load of each connection

從圖13(d)及表4可以看出，正向加載時，在阻尼器平直段厚度不小于U形截面段厚度的前提下，節點的屈服荷載隨著阻尼器平直段厚度的減小而逐漸降低，不過降低幅度較小，JD9相較于JD1的屈服荷載下降不到3%；負向加載時，翼緣處U形阻尼器平直段厚度的大小幾乎不影響節點的力學性能．當翼緣處U形阻尼平直段厚度不大于U形截面段厚度時，節點的正向荷載將大幅下降，JD8正向屈服荷載為146.7 N·m，而JD1正向屈服荷載為172.5 N·m，JD8相較JD1的正向屈服荷載降低了14.9%，這種現象產生的原因已在4.2中闡明．

表5給出了各節點極限荷載及延性系數．可以看出，JD1的負向極限荷載為284.2kN·m，于梁全截面塑性彎矩367kN·m接近．此外，通過表4可以看出，節點正向極限荷載均比負向極限荷載絕對值小，這是因為阻尼器在極限荷載狀態均發生了較大的變形，U形阻尼器在正向荷載下U形段高度由于擠壓變形而增加，在負向荷載作用下U形段高度由于拉伸變形而降低，通過公式(5)可知當U形段高度降低時阻尼器的抗拉承載力將增加．從表5可以看出各節點延性系數均達到了5.0以上，說明帶U形阻尼器梁柱節點具備良好的延性性能．

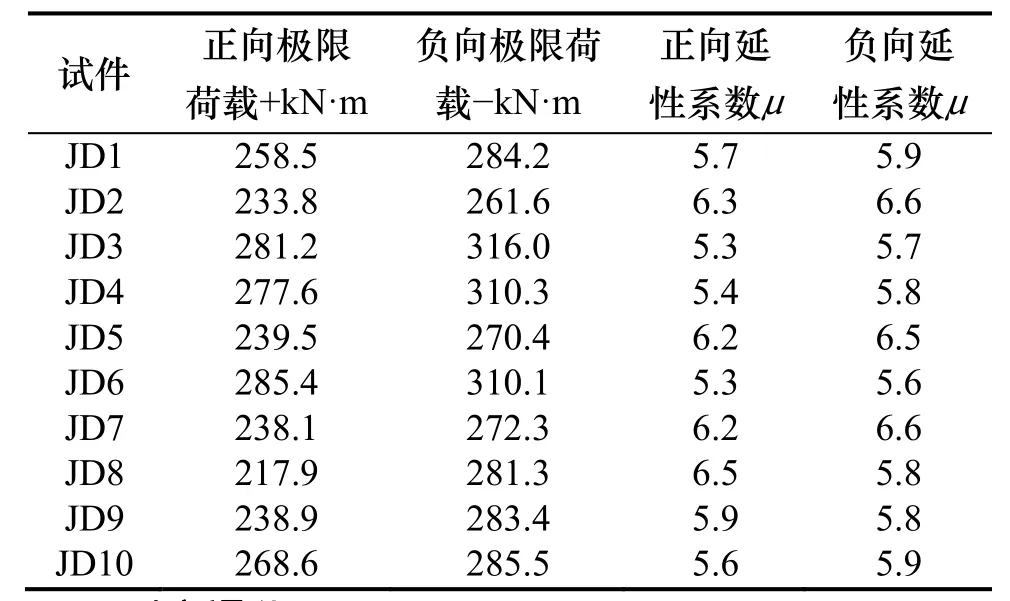
表5 各節點極限荷載及延性系數Tab.5 The ultimate load and ductility coefficient of each connection

3.4 剛度退化

分析的四組節點在循環荷載作用下的剛度曲線如圖14所示．

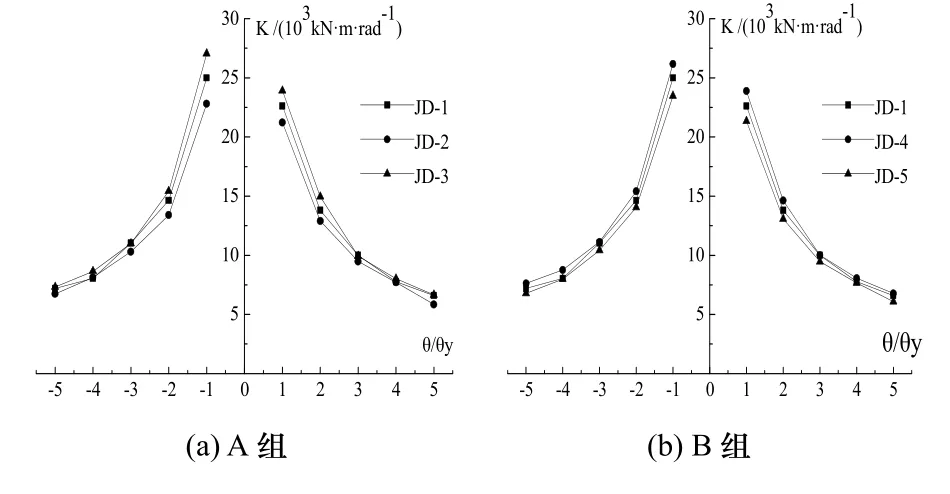
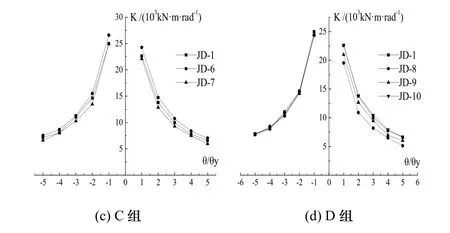
圖14 剛度退化曲線Fig.14 Stiffness degradation curves

各節點在加載過程中發生剛度持續退化，且在相同加載下節點的正向環線均比負向剛度略小．各節點的剛度退化曲線變化趨勢基本一致，且各曲線均勻無突變，隨著加載位移增加，節點的剛度退化速度逐漸減緩．

3.5 耗能能力

采用等效粘滯阻尼系數he來衡量節點的耗能能力[17]，he表達式為

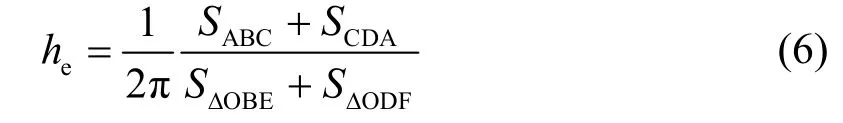
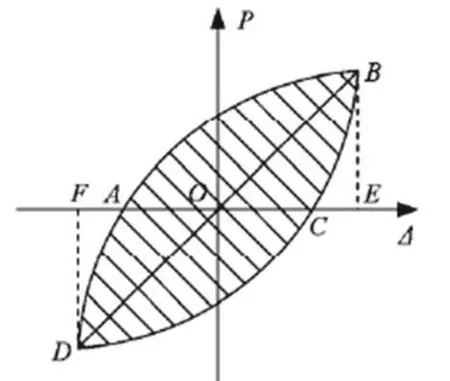
圖15 耗能計算簡圖Fig.15 Sketch for predicting energy dissipation

圖16為各節點在循環荷載作用下不同加載幅值對應的等效粘滯阻尼系數．

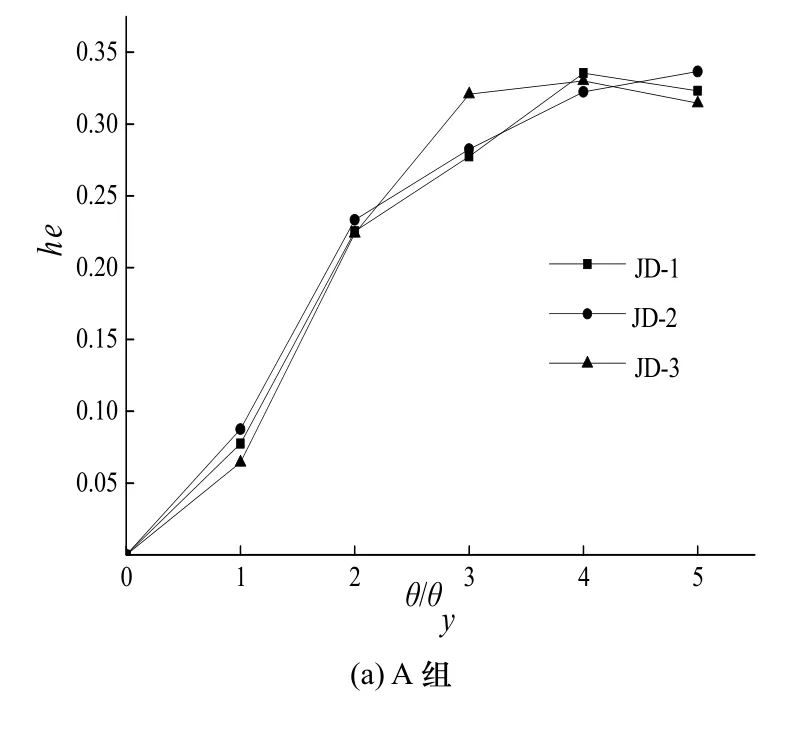
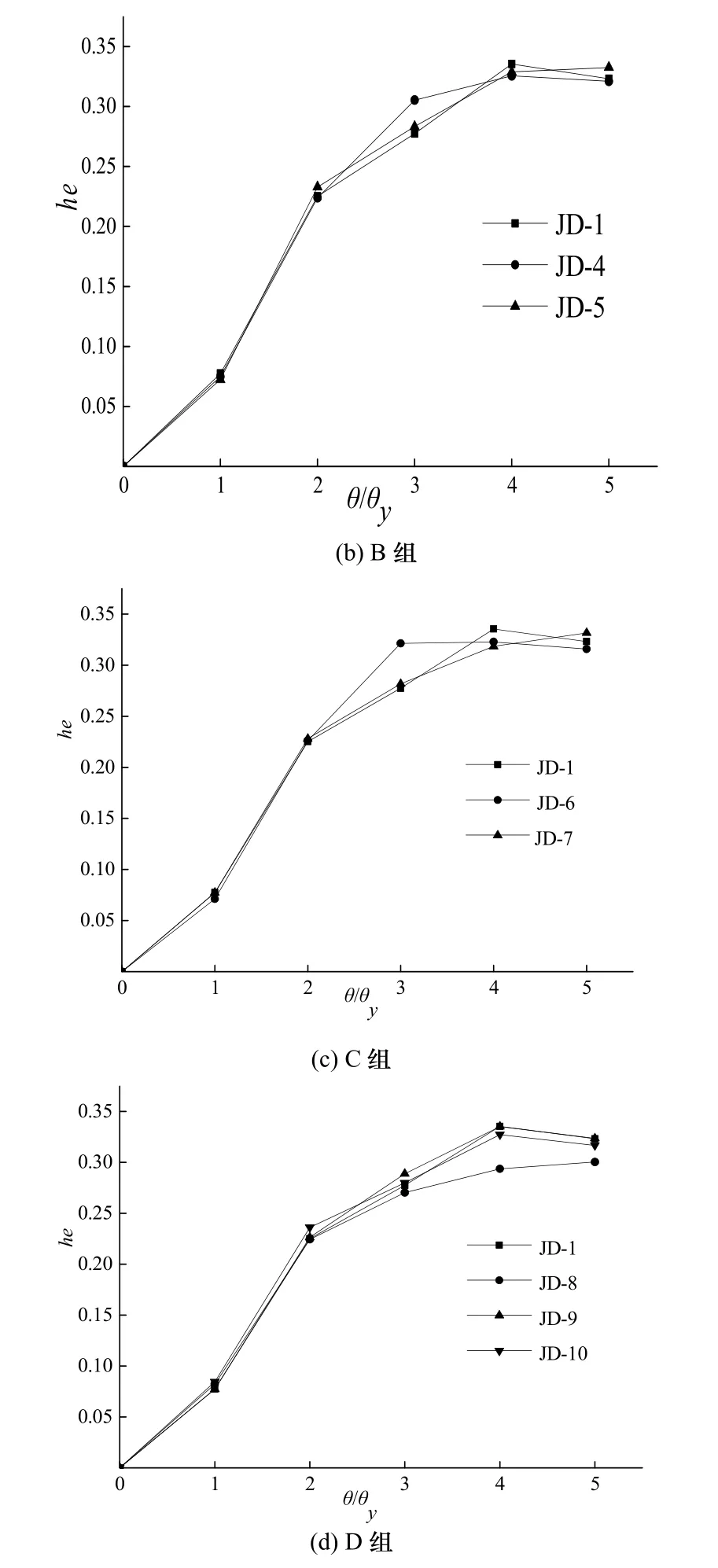
圖16 節點的等效粘滯阻尼系數heFig.16 Equivalent viscous damp coefficient he

從圖16(a)～(c)可以看出，節點的等效粘滯阻尼系數對阻尼器U形段截面的厚度、直段高度以及半徑不敏感，各節點在4倍屈服位移時等效粘滯阻尼系數最大．在三倍屈服位移時JD3、JD4及JD6的等效粘滯阻尼系明顯比JD1大，這是因為在三倍屈服位移加載幅值下這三個節點下翼緣處 U形阻尼器發生了滑移．從圖16(d)可以看出，改變U形阻尼平直段厚度對節點的等效粘滯阻尼系數影響不大，而當其厚度不大于U形段截面厚度時，節點的等效粘滯阻尼系數明顯下降，耗能能力顯著降低．

4 結論

論文對所提出的新型帶U形阻尼器梁柱強軸節點受力性能進行了有限元分析，得出以下結論：

(1) 提出的新型帶U形阻尼器梁柱強軸節點破壞時為U形阻尼器破壞，而梁和柱基本保持在彈性范圍，表明所提出的節點能有效保護主體結構在地震中不被破壞，同時震后易于修復．

(2) 提出的新型帶U形阻尼器梁柱節點具有飽滿、穩定的滯回曲線，表現出良好的滯回性能和良好的延性性能．

(3) 該節點的承載力主要由阻尼器U形截面段直段高度、厚度以及半徑控制，降低U形截面段直段高度、增加厚度和減小半徑都能提高節點的承載力，其中厚度對節點承載力的影響最大．

(4) U形阻尼平直段厚度不大于U形段截面厚度時，節點正向承載力及耗能能力將大幅降低．

References

[1] 崔鴻超. 日本兵庫縣南部地區地震震害綜述[J].建筑結構學報,1996,17(1): 2-13.CUI Hongchao. Review of earthquake damage in Kobe,Japan [J]. Journal of Building Structures, 1996, 17(1):2-13.

[2] MILLER D K. Lessons learned from the Northridge earthquake [J]. Engineering Structures, 1998, 20(4 /5 /6):249-260.

[3] NAKASHIMA M, INOUE K, TADA M. Classification of damage to steel buildings observed in the 1995 Hyogoken-Nanbu earthquake [J]. Engineering Structures,1998, 20(4 /5 /6): 271-281.

[4] 吳兆旗, 何田田, 姜紹飛, 等. 鋼結構梁柱連接節點抗震性能研究進展[J].福州大學學報(自然科學版),2011,39(5): 658-665.WU Zhaoqi, HE Tiantian, JIANG Shaofei, et al. Research advances in seismic performance of steel beam-to-column connections [J]. Journal of Fuzhou University (Natural Science Edition), 2011, 39(5), 658-665.

[5] 吳兆旗, 蘇建強, 姜紹飛, 等. 設置墊板的梁柱T形件連接節點抗震性能試驗研究[J].建筑結構學報,2012,33(12): 10-19.WU Zhaoqi, SU Jiangqiang, JIANG Shaofei, et al. Experimental investigation of seismic behavior f beam-to-column T-stub connected joints with inserted plates [J]. Journal of Building Structures, 2012, 33(12):10-19.

[6] KOETAKA Y, CHUSILP P, ZHANG Z, et al. Mechanical property of beam-to-column moment connections with hysteretic dampers for column weak axis [J]. Engineering Structures, 2005, 27(1) : 109-117.

[7] OH S H, KIM Y J, RYU H S. Seismic performance of steel structures with slit dampers [J]. Engineering Structures, 2009, 31(9): 1997-2008.

[8] 楊應華, 徐增武. 一種帶 U形耗能元件的易修復梁柱節點, ZL201320460254.2[P]. 2013.YANG Yinghua, XU Zengwu, An easily reparable beam-to-column connection with U-shaped damper.ZL201320460254.2[P]. 2013.

[9] 陳紹蕃．鋼結構[M].(第二版). 北京: 中國建筑工業出版社, 2009.Chen Shaofan. Steel Structure [M]. 2nd Ed. Beijing:China Architecture & Building Press, 2009.

[10] 徐增武. 帶 U形阻尼器梁柱節點的力學性能研究[D].西安:西安建筑科技大學, 2014.XU Zengwu. Mechanical properties of beam-to-column connections with U-shaped dampers[D]. Xi?an: Xi?an Univ. of Arch. & Tech., 2014.

[11] 陳驥. 鋼結構穩定理論與設計 [M]. (第五版)北京:科學出版社, 2011.CHEN Ji. Stability of steel structures: Theory and design[M]. 5th Ed. Beijing: Science Press, 2011

[12] CHASTEN C P, LU Lewu, DRISCOLL G C. Prying and shear in end-plate connection design [J]. Journal of Structural Engineering, ASCE, 1992,ll8(5):1295-1311.

[13] ECCS Technical Committee, Structural Safety and Loadings. Technical Working Group, Seismic Design. Study of design of building in earthquake zone[M].Belgium:Brussels ECCS General Secretariat, 1986.

[14] SAFFARI H, HEDAYAT A.A, NEJAD M. Poorsadeghi.Post-northridge connections with slit dampers to enhance strength and ductility [J]. Journal of Constructional Steel Research, 2013, 80(1): 138-152.

[15] 中華人民共和國行業標準.建筑抗震試驗方法規程:JGJ101-96[S].北京:中國建筑工業出版社, 1997.Industry Standard of People's Republic of China. Specification of testing methods for earthquake resistant building: JGJ101-96[M]. Beijing: China Architecture &Building Press, 1997.

[16] 龍曉鴻, 李黎, 唐家祥. I－型鋼槽阻尼器的 ANSYS仿真分析[J].華中科技大學學報(自然科學版),2002,30(8):79-81.LONG Xiaohong, LI Li, TANG Jiaxiang. Simulation analysis of I-shape steel slit damper by ANSYS [J]. Journal of Huazhong University of Science and Technology:(Nature Science Edition), 2002, 30(8):79-31.

[17] 聶建國, 黃遠, 樊建生. 考慮樓板組合作用的方鋼管混凝土組合框架受力性能試驗研究[J]. 建筑結構學報,2011,32(3): 99-108.NIE Jianguo, HUANG Yuan, FANG Jiangyuan, Experimental study on load-bearing behavior of rectangular CFST frame considering composite action of floor slab[J].Journal of Building Structures, 2011, 32(3): 99-108.