高延性混凝土單軸受壓本構模型研究

鄧明科，潘姣姣，秦 萌,2，劉海勃

(1．西安建筑科技大學土木工程學院，陜西 西安710055；2．成都天華西南建筑設計有限公司，四川 成都610016)

高延性水泥基復合材料[1-4](engineered cementitious composite，ECC)是一種具有高強度、高韌性和高耐損傷能力的新型材料，在拉伸和剪切荷載下表現出良好的多裂縫開展和應變硬化特性，可顯著提高混凝土材料的韌性和耐損傷能力，在土木工程領域具有廣泛的應用前景．為便于ECC在混凝土結構中的應用，本課題組采用ECC設計理論制備了高延性混凝土(high ductile concrete，HDC)，并對其進行了受壓、受彎與受拉力學性能的試驗研究[5-8]，但是對高延性混凝土的單軸受壓應力-應變關系仍需進一步的研究．

混凝土單軸受壓本構關系是研究結構構件承載力和變形能力的主要依據，對于構件的彈塑性全過程分析和結構延性設計均具有重要的意義．李艷等通過單軸受壓試驗，得到了高韌性PVA-FRCC單軸受壓本構方程[9]；焦楚杰等通過試驗得出了鋼纖維高強混凝土單軸壓縮本構方程[10]；徐世烺等研究了超高韌性水泥基復合材料的單軸受壓應力-應變全曲線和非線性分析模型[11]．前期研究表明[12]，與普通混凝土相比，高延性混凝土單軸受壓時，基體內部的纖維橋聯作用，使試件縱向受壓時受到穩定的橫向約束力，其抗壓韌性和受壓變形能力明顯提高，因此，高延性混凝土的單軸受壓本構模型與普通混凝土有較大區別．

本文選取尺寸為100 mm×100 mm×300 mm的棱柱體試件，進行高延性混凝土單軸受壓試驗，并考慮纖維摻量、粉煤灰摻量、水膠比和砂膠比對應力-應變曲線形狀及其特征點的影響，提出適用于高延性混凝土的單軸受壓本構模型，為高延性混凝土結構設計和非線性數值模擬提供了理論依據．

1 試驗概況

試驗采用的高延性混凝土基本組成為：水泥(P·O 42.5R)、I級粉煤灰、涇陽天然河砂(最大粒徑為1.18mm)、礦物摻合料、PVA纖維和水．PVA纖維的具體參數見表1，試驗配合比設計見表2，其中配合比1為不含纖維的水泥砂漿基體對比試件．

表1 PVA纖維性能指標Tab.1 Properties of PVA fiber

表2 試驗配合比設計Tab.2 Mix design for experimental program

2 試驗結果分析

2.1 試件破壞形態

砂漿基體的受壓破壞過程與混凝土類似，試件達到峰值荷載以后發生崩裂，并立即喪失承載力，發生明顯的脆性破壞．

高延性混凝土試件縱向受壓時，橫向產生拉伸變形．試件的上、下端因受到加載墊板的約束而橫向變形較小，中部雖受到加載墊板的約束力很小，但受到基體內部纖維橋聯應力的約束作用明顯．由于 HDC良好的拉伸應變硬化性能，試件中部的橫向拉伸變形始終可以受到纖維橋聯應力的有效約束，使基體內部縱向裂縫的出現和擴展明顯滯后．直到試件橫向拉伸變形超過了 HDC的極限拉應變時，基體內部的纖維被拔出或拉斷，試件中部受到的橫向約束力失效，在最薄弱處出現縱向裂縫并上下貫通形成一條主裂縫．試件破壞過程中，主斜裂縫兩側試塊發生明顯錯動，試件承載力基本保持不變．由于纖維的橋聯作用，試件受壓破壞以后仍保持一定的剩余承載力和較好的完整性．試件縱向受壓的裂縫分布及破壞形態如圖1所示．

圖1 HDC試件裂縫分布及破壞形態Fig.1 Crack distribution and failure mode of HDC specimens

2.2 單軸受壓應力-應變曲線

試驗測得各組試件單軸受壓的應力-應變曲線如圖2所示．從圖2中可以看出，本次試驗測得的高延性混凝土單軸受壓破壞過程和應力-應變曲線具有以下特點：

加載初期，曲線上升段的應力-應變基本保持為線彈性關系，斜率基本保持不變；當應力達到抗壓強度的80%左右時，纖維提供的橫向約束力達到最大值，由于內部裂縫的擴展，應變增長速度加快，使應力-應變曲線斜率減小；試件達到峰值荷載時，纖維提供的橫向約束力失效，試件中部裂縫迅速擴展并向上下兩端延伸，荷載迅速降低；當應力下降至峰值荷載的 10%～20%，應力-應變曲線下降段出現一個拐點(曲率最大點)，之后曲線趨于平緩．

圖2 HDC單軸受壓應力-應變曲線Fig.2 Uniaxial compression stress-strain curves of HDC

2.3 單軸受壓應力-應變曲線特征點

表 3給出了各組試件應力-應變曲線的特征點及其對應的應力和應變值．由圖2和表3可以看出，砂漿基體(配合比1)對應的峰值應變為0.002 1，與《混凝土結構設計規范》[15]相應混凝土的峰值應變接近．高延性混凝土的峰值變形較砂漿基體試件均有明顯提高，9組不同配合比HDC的峰值應變可達砂漿基體的2.61～3.15倍，表明HDC達到峰值荷載以前的變形能力得到明顯提高，具有約束混凝土受 力特點．

表3 HDC受壓本構模型參數Tab.3 Parameters of HDC compression constitutive model

圖3 各因素對受壓應力-應變曲線各特征值的影響Fig.3 Influence of various factors on characteristic value of compression stress-strain curves

2.4 各因素對應力-應變曲線特征點的影響分析

根據表3的試驗結果，可得纖維摻量、水膠比、粉煤灰摻量和砂膠比四種因素對 HDC單軸受壓應力-應變曲線特征點應變值的影響如圖3．對各因素的影響分析如下：

(1) 纖維摻量

高延性混凝土基體內部亂向分布的短纖維能有效阻止內部微裂縫的產生和發展，提高了試件單軸受壓的變形能力．由表3和圖3(a)分析可得，隨著纖維摻量的增加，高延性混凝土應力-應變曲線的峰值應變提高不明顯，但極限壓應變均有明顯提高．當纖維摻量由1%增加到2%時，ε0.85、ε0.5和ε0.2分別提高了33.06%、39.73%和62.85%．

(2) 水膠比

水膠比減小，拌合物的和易性降低，導致基體內部纖維分散不均勻，使得纖維的增韌和阻裂作用減弱．由圖3(b)可以看出，水膠比為0.26的試件極限壓應變比水膠比為0.29和0.32的試件均有所降低．由于本次試驗中水膠比的變化范圍較小，水膠比對試件單軸受壓變形能力的影響較小．

(3) 粉煤灰摻量

由表3和圖3(c)可以看出，當粉煤灰摻量由40%增加至50%時，試件的峰值應變和極限壓應變均有明顯提高，這是因為粉煤灰可以改善纖維與基體之間的界面特性，有助于發揮纖維的增韌作用，在一定程度上提高試件的受壓變形能力．但粉煤灰摻量過高，試件抗壓強度有所降低．

(4) 砂膠比

砂膠比由0.24增加至0.36時，試件變形能力提高并不明顯；增大至0.48時，高延性混凝土的抗壓強度有所提高，但纖維與基體之間的摩擦力增大，使得纖維大多被拔斷，在一定程度上降低了材料的拉伸變形能力，導致其受壓變形能力降低．因此，砂膠比過高，試件單軸受壓的極限壓應變明顯降低．

3 單軸受壓本構關系

3.1 單軸受壓應力-應變曲線

圖4 HDC單軸受壓無量綱應力-應變曲線Fig.4 Uniaxial compression dimensionless stress-strain curves of HDC

從圖4可大致看出HDC應力-應變曲線的特點：其走向規律與混凝土相似，由上升段和下降段組成；曲線上升段斜率單調下降；在峰值應力點，曲線斜率降為零；曲線下降段，先出現一個拐點，接著出現曲率最大點，然后曲線趨于平緩．

根據以上分析，結合參考文獻[14]，高延性混凝土的應力-應變曲線應滿足以下條件：

3.2 本構模型的確定

基于高延性混凝土單軸受壓應力-應變曲線的形狀及其特點，可采用以下三種模型：

(1) 過鎮海建議的分段式曲線方程[14]：

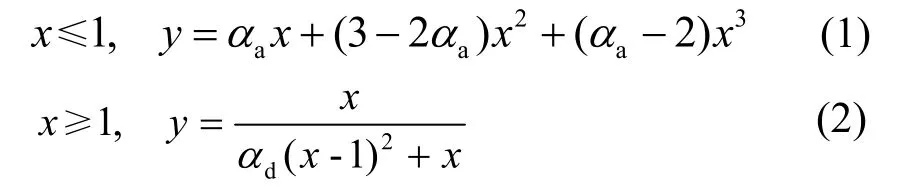
(2) Sargin建議的有理分式曲線方程[13]：

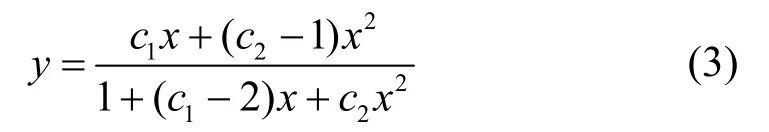
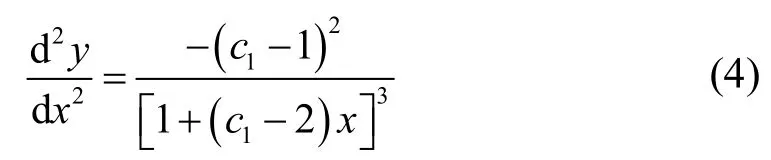
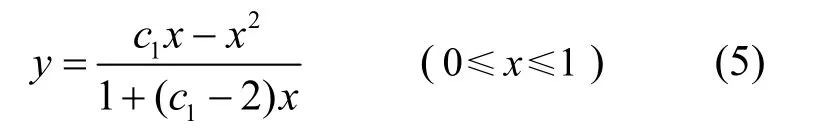
根據條件⑥，③下降段應力-應變曲線可表示為：

(3) Saenz建議的有理分式曲線方程[13]：

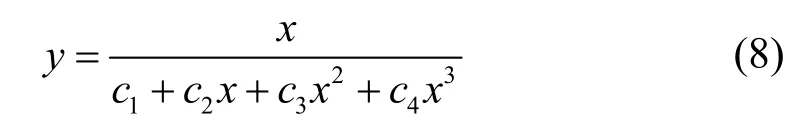
因此上升段應力-應變曲線可表示為：

上述三種模型的上升段和下降段在曲線峰值點連續，并符合上述全部幾何特征(①～⑦)的要求．為了便于對比和分析三種模型，統一將上升段曲線方程中的參數設為aα，下降段曲線方程中的參數設為dα，二者均具有相應物理意義[14]．

上升段參數aα為初始彈性模量(E0)與峰值割線模量(Eg)的比值；下降段參數當y≡1，峰值點后為水平線(全塑性)；當dα=∞時，y≡0，峰值點后為垂直線(脆性)．

根據條件②，可推出三種模型中參數aα的取值范圍．經過推導與代換，三種模型的曲線方程及其參數取值范圍如下：

(1) 過鎮海建議的分段式曲線方程(模型1)：

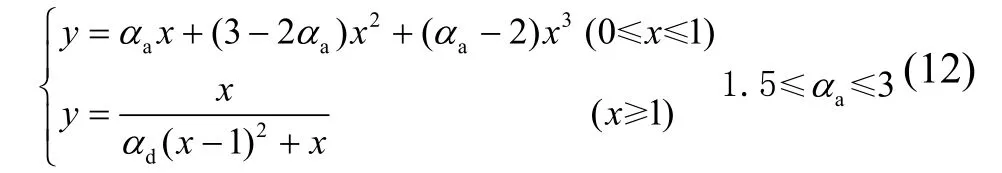
(2) Sargin建議的有理分式曲線方程(模型2)：

(3) Saenz建議的有理分式曲線方程(模型3)：

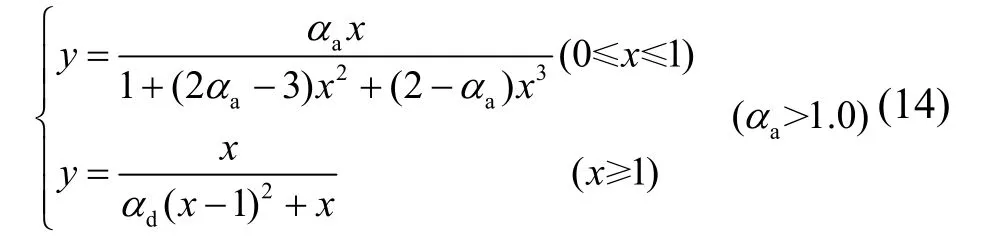
可見，三種模型的應力-應變曲線上升段方程有所差異，下降段均采用同一方程．

3.3 本構模型參數的確定

與普通混凝土相比，HDC的單軸受壓應力-應變曲線具有以下特性：

(1) 纖維的橫向約束作用，使試件彈性段明顯變長，達到峰值應力80%以前均接近線性，縱向裂縫的產生和發展滯后．

(2) 基體內部的纖維橋聯作用，使HDC的峰值應變明顯提高，具有約束混凝土的受力性能．

(3) 達到峰值荷載以后，纖維的橫向約束作用失效，曲線下降段更陡峭．

(4) 試件破壞以后仍具有一定的殘余強度，曲線下降段出現拐點．

因此，高延性混凝土單軸受壓應力-應變曲線的上升段參數aα和下降段參數dα與普通混凝土應有所不同．

基于上述分析，依據最小二乘法，對高延性混凝土單軸受壓應力-應變曲線進行非線性回歸，得到三種模型的參數及其相關系數如表4所示．由曲線參數的物理意義可知，上升段參數aα越大，峰值應力與彈性極限應力的差值越大，下降段參數dα越小，曲線下降越平緩．

由表4可見，模型1的上升段參數aα與試驗結果相差較大，其相關系數明顯小于模型 2和模型3．考慮配合比設計中各因素變化的影響，對模型2和模型3上升段參數和下降段參數進行如下分析：

隨著纖維摻量的增加，單軸受壓應力-應變曲線上升段參數aα逐漸增大，下降段參數dα逐漸減小，表現為曲線的上升段和下降段均逐漸趨于平緩，曲線下方所包含的面積逐漸增大，說明纖維摻量增大，試件受壓破壞過程中吸收的能量增加，試件的抗壓韌性提高．水膠比減小，aα逐漸減小，dα逐漸增大，表現為曲線的上升段和下降段逐漸陡峭，曲線下方所包含的面積有所減小，試件的抗壓韌性有所降低．粉煤灰摻量增大以及砂膠比減小，aα逐漸增大，dα逐漸減小，曲線下包的面積有所增大，試件的抗壓韌性提高．

以上三種本構模型的無量綱應力-應變曲線與HDC受壓試驗曲線對比如圖5所示．通過對比表4中的相關系數和圖5中的曲線可以發現：采用模型2和模型3得到的擬合曲線與試驗曲線吻合較好，其中模型2最接近于試驗曲線．

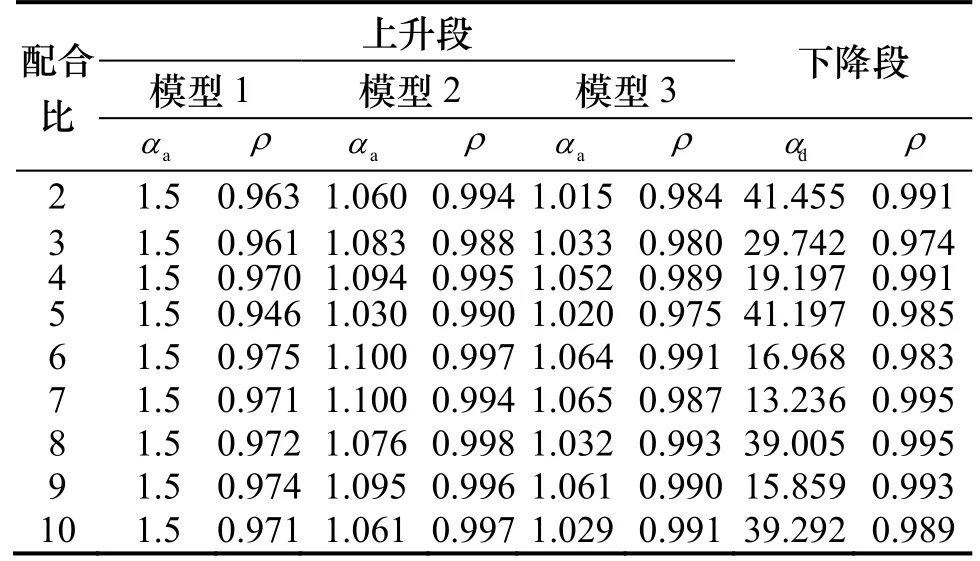
表4 HDC應力-應變曲線參數Tab.4 Parameters of HDC stress-strain curve

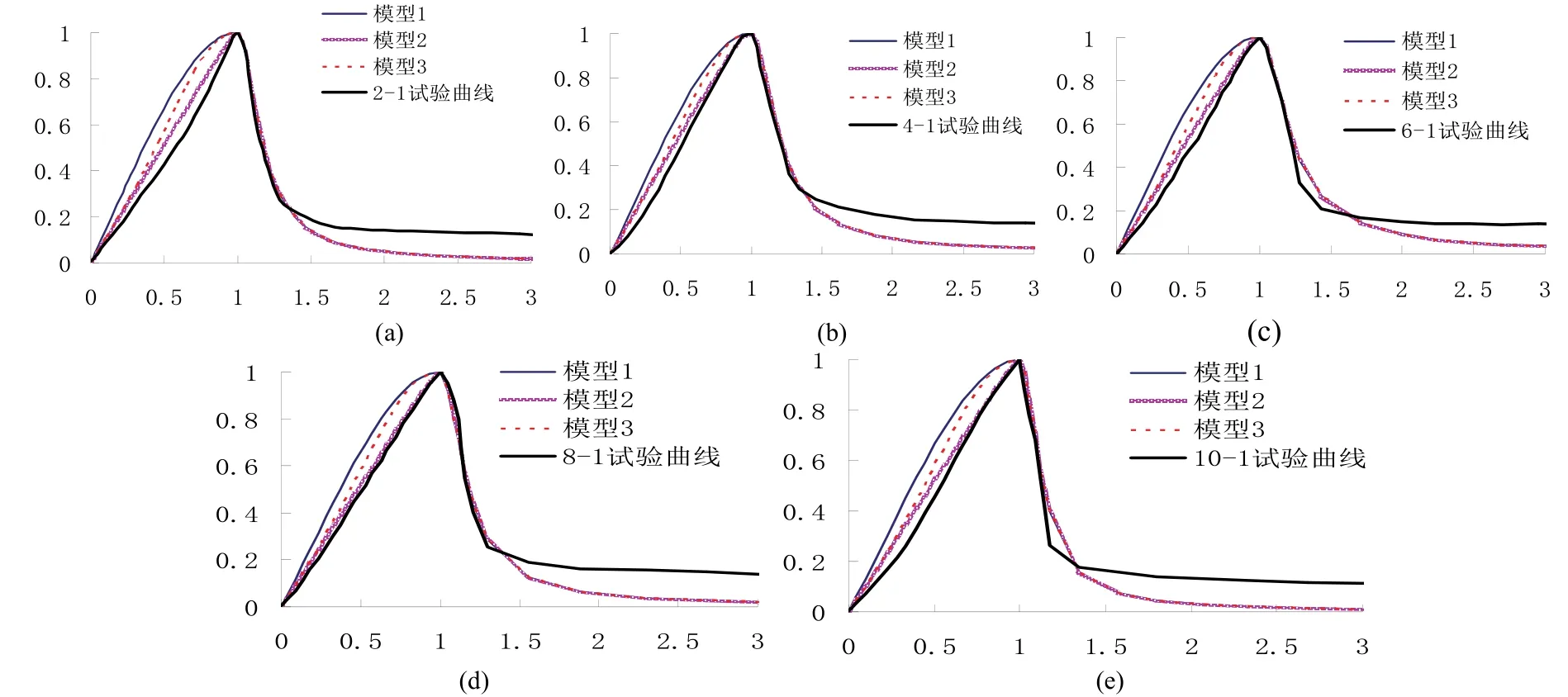
圖5 實測應力-應變全曲線與本構模型的對比Fig.5 Comparison between stress-strain curve and constitutive model

4 結論

(1) 高延性混凝土試件單軸受壓時，試件中部受到基體內部纖維橋聯應力的約束作用，縱向裂縫的產生和發展滯后，試件破壞以后始終具有10～20%的剩余承載力和較好的完整性，表現出較高的抗壓韌性．

(2) 纖維摻量、粉煤灰摻量和砂膠比對HDC單軸受壓應力-應變曲線的特征點均有一定的影響．纖維摻量增大，HDC的極限壓應變明顯提高；粉煤灰摻量增加，HDC的峰值應變和極限壓應變均有明顯提高，但抗壓強度有所降低；砂膠比增大，HDC的抗壓強度有所提高，但極限壓應變明顯降低．

(3) 與普通混凝土相比，HDC單軸受壓應力-應變曲線的彈性段明顯變長，峰值應變明顯提高，曲線下降段更陡峭并出現明顯拐點，其上升段參數aα和下降段參數dα也有所不同．

(4) 依據最小二乘法，對三種HDC單軸受壓本構模型上升段參數和相關系數進行分析發現，采用模型2和模型3得到的擬合曲線與試驗曲線吻合較好，其中模型2最接近于試驗曲線．

References

[1] LI V C, LEUNG C K Y. Steady state and multiple cracking of short random fiber composites [J]. Journal of Engineering Mechanics, ASCE, 1992, 188(11): 2246-2264.

[2] LI V C. ECC–tailored composites through micromechanical modeling[C]//Fiber Reinforced Concrete: Present and the Future. Montreal: Canadian Society of Civil Engineering, 1998: 64-97.

[3] LI V C. On engineered cementitious composites (ECC): a review of the material and its applications [J]. Journal of Advanced Concrete Technology, 2003, 1(3): 215-230.

[4] LI V C, WANG S, WU C. Tensile strain-hardening behavior of PVA-ECC [J].ACI Materials Journal,2001,98(6): 483- 492 .

[5] 鄧明科, 孫宏哲, 梁興文, 等. 延性纖維混凝土抗彎性能的試驗研究[J]. 工業建筑, 2014, 44(5): 85-90.DENG Mingke , SUN Hongzhe, LIANG Xingwen, et al.Experimental study of flexural behavior of high ductile fiber reinforced concrete [J]. Industrial Construction,2014, 44(5):85-90.

[6] 鄧明科, 孫宏哲, 梁興文, 等. 延性纖維混凝土抗壓與抗彎性能研究[J]. 工業建筑, 2014, 44(10): 115-121.DENG Mingke, SUN Hongzhe, LIANG Xingwen, et al.Experimental study of compressive behavior and flexural behavior of high ductile fiber reinforced concrete [J].Industrial Construction, 2014, 44(10): 115-121.

[7] 鄧明科, 秦萌, 梁興文. 高延性混凝土抗壓性能試驗研究[J]. 工業建筑, 2015, 45(4) : 120-126.DENG Mingke, QIN Meng, LIANG Xingwen. Experimental study of compressive behavior of engineered cementitious composities[J]. Industrial Construction,2015, 45(4): 120 -126.

[8] 寇佳亮, 鄧明科, 梁興文. 延性纖維增強混凝土單軸拉伸性能試驗研究[J]. 建筑結構, 2013, 43(1): 59-64.KOU Jialiang, DENG Mingke, LIANG Xingwen. Experimental study of uniaxial tensile properties of high ductile fiber reinforced concrete [J]. Building Structure,2013, 43(1): 59-64.

[9] 李艷,劉澤軍. 高韌性PVA-FRCC單軸受壓力學性能及本構關系[J].建筑材料學報, 2014,17(4): 606-612.LI Yan, LIU Zejun. The uniaxial compressive mechanical properties and constitutive relation of high toughness PVA–FRCC.[J]. Journal of Building Structures,2014,17(4): 606-612 .

[10] 焦楚杰, 孫偉, 秦鴻根, 等. 鋼纖維高強混凝土單軸受壓本構方程[J]. 東南大學學報(自然科學版),2004,34(3): 366-369.JIAO Chujie, SUN Wei, QIN Honggen, et al. The uniaxial compression constitutive equation of steel fiber reinforced high strength concrete [J]. Journal of Southeast University (Natural Science Edition),2004,34(3):366-369.

[11] 徐世烺, 蔡向榮, 張英華. 超高韌性水泥基復合材料單軸受壓應力-應變全曲線試驗測定與分析[J].土木工程學報,2009,42(11): 79-85.XU Shilang, CAI Xiangrong, ZHANG Yinghua. Experimental measurement and analysis of the axial compressive stress-strain curve of Ultra High Toughness Cementitious Composities[J]. China Civil Engineering Journal, 2009, 42(11): 79-85.

[12] 鄧明科,劉海勃,秦萌,等. 高延性纖維混凝土抗壓韌性試驗研究[J].西安建筑科技大學學報(自然科學版),2015,47(5):660-665, 677.DENG Mingke, LIU Haibo, QIN Meng, et al. Experimental study research on compressive toughness of the high ductile fiber reinforced concrete[J].J. of Xi’an Univ.of Arch. & Tech.(Natural Science Edition), 2015,47(5):660-665,677.

[13] 過鎮海.混凝土的強度和變形(試驗基礎和本構關系)[M]. 北京: 清華大學出版社,1997.GUO Zhenhai.The strength and deformation of concrete(experimental basis and constitutive relation), principle and application [M]. Beijing: Tsinghua University Press,1997.

[14] 過鎮海,時旭東.鋼筋混凝土原理和分析[M]. 北京: 清華大學出版社,2003.GUO Zhenhai, SHI Xudong. Reinforced concrete theory and analyse[M]. Beijing: Tsinghua University Press,2003.

[15] 中華人民共和國住房和城鄉建設部. 混凝土結構設計規范: GB 50010-2010 [S]. 北京: 中國建筑工業出版社.Ministry of Housing and Urban-Rural Development of People's Republic of China. Code for design of concrete structures: GB 50010-2010[S]. Beijing: China Building Industry Press.