含三個時間分數階導數的反常擴散方程求解與微分階數反演

孫春龍，李功勝，賈現正，杜殿虎

(山東理工大學 理學院， 山東 淄博255049)

?

含三個時間分數階導數的反常擴散方程求解與微分階數反演

孫春龍，李功勝，賈現正，杜殿虎

(山東理工大學 理學院， 山東 淄博255049)

摘要：對于一類帶有三個時間分數階的一維反常擴散問題,基于Caputo意義下時間分數階導數的離散,給出了一個有限差分求解格式,并利用分離變量法及Laplace變換得到該問題的解析解.進一步應用同倫正則化算法,根據內點處的濃度觀測數據對確定微分階數的反問題進行數值反演,并討論時間-空間步長及數據擾動等因素對反演算法的影響.

關鍵詞：時間分數階導數； 含三個時間分數階的擴散； 反問題； 同倫正則化算法； 數值反演

在過去的幾十年,分數階偏微分方程在反常擴散現象模擬等領域開始發揮重要作用,其對復雜系統的描述具有建模簡單、參數物理意義清楚、描述準確等優勢.陳文案[1]較詳細地描述了分數階微積分理論在復雜力學行為建模和數值模擬方面的研究成果，強調分數階微積分建模的物理和力學背景和概念.分數階反常擴散方程是由經典擴散方程推廣而得到的,按照其含有的時間-空間導數的形式可分為三類：分別是時間分數階擴散、空間分數階擴散和空間-時間分數階擴散.當通常的整數階擴散方程中關于時間變量的1階導數換為α(0<α≤1)時,得到時間分數階擴散方程；當整數階擴散方程中關于空間變量的2階導數換為α(0<α≤2)時,得到空間分數階擴散方程；而當整數階擴散方程中關于時間與空間變量的整數階導數都換為相應的分數階導數時,就得到空間-時間分數階擴散方程.

對于時間分數階擴散方程正問題的研究,劉發旺等人做了很多研究.于強與劉發旺[2]給出了時間分數階反應-擴散方程的隱式差分近似；沈淑君與劉發旺[3]推導出了時間分數階擴散方程初邊值問題的數值解,并提出了方程的顯式守恒差分格式,證明了此格式的穩定性和收斂性,然后將得到的結果推廣到時間分數階對流-擴散方程.劉法旺和Meerschaert[4]等人,給出了含有多個時間分數階的擴散-波動方程的數值計算方法,并討論了隱式差分求解格式.Luchko[5]與Liu等[6]分別研究了多個時間分數階的對流-擴散方程,得到了廣義Mittag-Leffler函數形式的解析解.

對于分數階擴散中的反問題研究,已引起了大家的關注.程晉等[7]研究了一維時間分數階擴散中由單個邊界點處的連續測量值同時確定微分階數與空間依賴擴散系數的反問題,應用特征展開方法證明了該反問題解的唯一性.劉繼軍和Yamamoto[8]應用準可逆性正則化(quasi-reversibilityregularization)方法探討了一個時間分數階擴散中由終值數據恢復初始狀態的倒向反問題.鄭光輝與魏婷等[9-10]應用Fourier譜正則化方法研究了帶狀區域一維時間分數階對流擴散的Cauchy問題與空間Riesz分數階擴散的倒向反問題.Sakamoto與Yamamoto[11]利用特征分解方法探討了時間分數階擴散-波動方程倒向反問題的適定性.徐翔、程晉與Yamamoto等[12-13]研究了具有1/2階分數階導數的時間分數階擴散方程的Carleman估計方法,這是構建分數階擴散相關反問題條件穩定性的新思路.熊向團等[14]構建了時間分數階二維熱傳導方程的反向熱傳導問題的一種條件穩定性,李功勝等[15]利用最佳攝動量算法對于一維時間分數階擴散方程的空間依賴的擴散系數進行了有效的數值反演,魏婷等[16]基于邊界元離散提出一種正則化方法,研究了一維時間分數階擴散方程中時間依賴源項的重建問題.

本文將探討含有三個時間分數階導數的一維反常擴散方程求解及確定微分階數的反演問題.首先利用有限差分法給出正問題數值求解的差分格式,同時利用分離變量法及拉普拉斯變換得到正問題的解析解表達式,并且給出正問題的數值算例.進一步,應用同倫正則化算法對反常擴散方程中的三個時間分數階微分階數進行數值反演,給出數值反演算例,并討論時間空間步長及數據擾動水平等因素對反演算法的影響.

1正問題及其數值求解

考慮區域Ω=(0,l)×(0,T)上含三個時間分數階導數的一維反常擴散方程

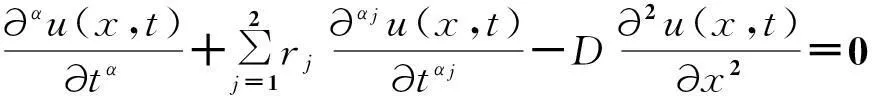
(1)

其中(x,t)∈Ω;D>0是擴散系數,α∈(0,1)和αj(j=1,2)∈(0,1)是時間分數階導數的微分階數，且0<α2<α1<α<1.對于方程(1),給定非零初值條件和第一類零邊值條件:

u(x,0)=f(x),u(0,t)=u(l,t)=0

(2)

這樣,由方程(1)及初邊值條件(2)就構成含三個時間分數階導數的一維反常擴散方程的正問題.下面給出這個正問題求解的一個有限差分格式，并運用分離變量法推導其解析解的表達式.

1.1正問題求解的差分格式

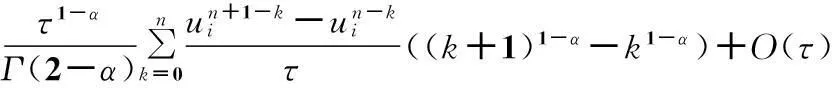
(3)

(4)

對于方程中的整數階導數項,按照通常的差分離散方法,即有

(5)

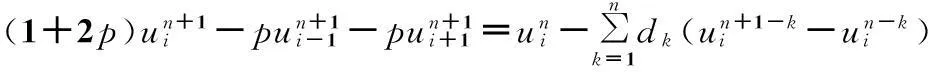
(6)

1.2正問題的解析解

本小節利用分離變量法及Laplace變換推導正問題的解析解.

設u(x,t)=X(x)T(t),代入方程可得

(7)

(8)

(9)

(10)

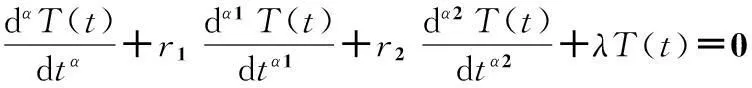
(11)

(12)

應用Laplace變換,得到

(13)

代入(12)式,可得

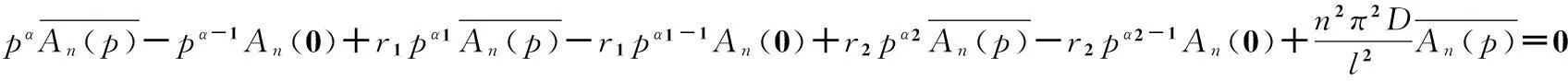
記c=Dλn為常數,可得

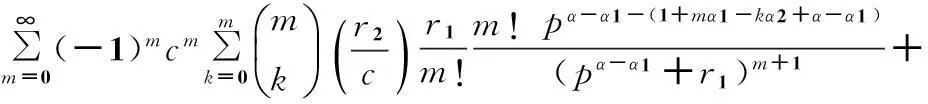
(14)

(15)

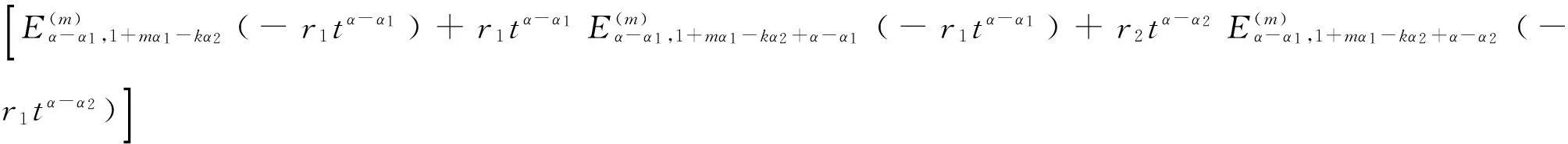
于是求得解析解為

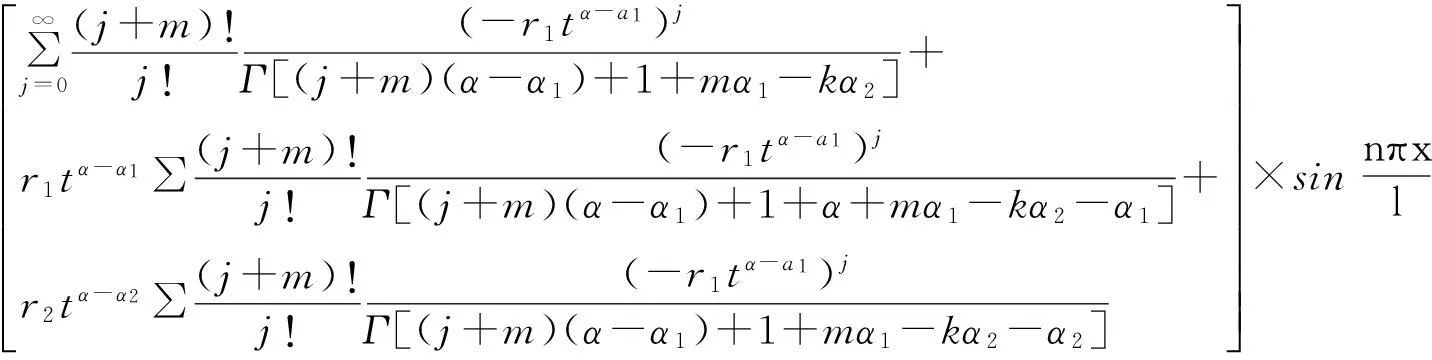
(16)

1.3數值試驗

利用上一節的有限差分法進行數值計算,取l=π,T=1,且離散點數M=100,N=100，微分階數α=0.8,α1=0.5,α2=0.3,擴散系數D=1,系數r1=0.5,r2=0.5.另外,取初始函數u(x,0)=f(x)=sinx.此時解析解可表示為

(17)

對上述解析解,級數取前50項截斷計算,記數值解u*(x,t),相對誤差表示為Err=‖u(x,t)-u*(x,t)‖2/‖(u,t)‖2.數值結果分別列于表1～表3和圖1.

表2 時間步長對解誤差的影響(t=0.5)

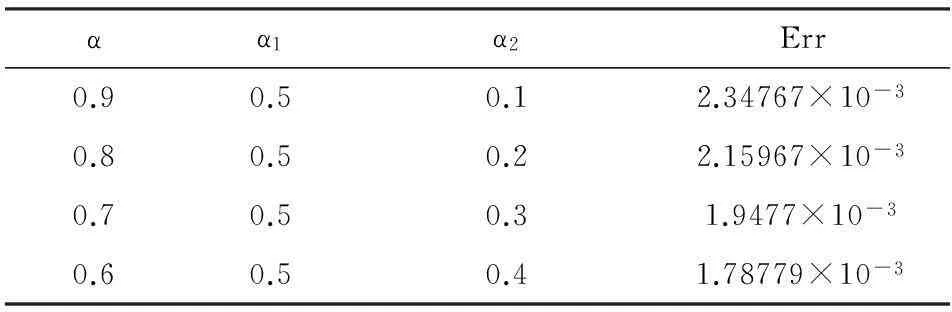
表3　不同微分階數對正問題求解的影響(t=0.5)

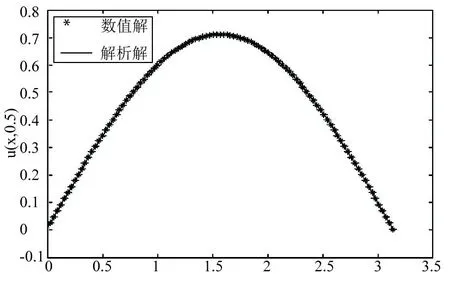
圖1 　t=0.5時的數值解與解析解

從表1的計算結果可以看出,空間步長對誤差的影響不大;由表2的計算結果可以看出,隨著時間步長的減小,誤差逐漸減小;由表1、表2及圖1的結果可以看到，正問題的數值解和解析解吻合的較好.從表3看出,時間微分階數對正問題求解具有一定的影響,微分階數越接近,解誤差有所減小.

2確定微分階數的反問題與反演算法

2.1反問題的提出

假設方程(1)中的時間微分階數未知,那么為了確定各個微分階數的值,需要補充關于正問題解的部分條件信息,并聯合正問題(1)～(2)形成一個確定微分階數的反問題.本文給定內點x=x0,時刻tj(j=1,2,…，N)的觀測值為附加數據,記為u(x0,tj)=θ(tj),則可定義附加數據向量V：

(18)

這樣,由附加數據(18)聯合正問題(1)～(2)構成了一個確定微分階數(α,α1,α2)的數值反演問題.下面給出同倫正則化算法,并對上述確定微分階數的反問題進行數值反演模擬.

2.2同倫正則化算法

記a=(α,α1,α2),利用上一節的差分方法求解正問題可得其解,并在x=x0處賦值,記之為u(x0,t;a),這可以看作對應于輸入數據a=(α,α1,α2)的一個計算輸出.

min‖U(a)-V‖2

(19)

為了克服病態性,應用同倫思想可將上式轉化為如下極小值問題：

min{(1-λ)‖U(a-V‖2+λ‖a‖2}

(20)

(21)

根據同倫正則化思想,上述極小問題(20)的求解又轉化為對于給定的an,通過求解最佳攝動量δan進而確定an+1的一種迭代算法：an+1=an+δan,n=0,1,2，…

(22)

(23)

將u(x0,tj;an+δan)在an處作泰勒展開,并略去高階項,可以得到

則目標函數F(δan)可近似表為

(24)

(25)

式中ω為數值微分步長.不難驗證泛函極小問題等價于求解規范方程：

((1-λ)GTG+λI)δan=(1-λ)GT(V-aU)，

(26)

則得到每一步迭代的最優攝動量δan的計算公式：

δan=((1-λ)GTG+λI)-1(1-λ)GT(V-U)

(27)

對于給定的精度eps,判斷‖δan‖≤eps是否成立,若滿足則δan即為所求;否則由式(22)得到an+1,再通過規范方程繼續求解.

3數值反演

本節應用同倫正則化算法對確定微分階數的反問題(1)～(2)及(18)進行數值反演.取初始函數f(x)=sinx,以下若無特殊說明,正問題計算中均取l=π,擴散系數D=1,終值時刻T=1,且M=100,N=100.附加數據取為在x0=0.5處的觀測數據，數值微分步長ω=0.01,停止準則eps=1e-6,預估迭代次數N0=5,β=0.8,設式(1)中r1=r2=0.5,取α=0.9,α1=0.7,α2=0.5，則微分階數真值a=(0.9，0.7，0.5)，ainv表示反演解,Err=‖ainv-a‖2/‖a‖2表示反演解與真解的誤差.

3.1附加數據不帶擾動的情形

(1)時間步長對反演結果的影響

令初始迭代值a0=(0.3,0.2,0.1),反演計算結果列于表4,n表示迭代次數.

表4　時間步長對反演結果的影響

表5　空間步長對反演結果的影響

由表4可以看出,時間步長對反演結果影響不大,只是隨時間步長的變小迭代的次數稍微減少.

(2)空間步長對反演結果的影響

取初始迭代值a0=(0.3,0.2,0.1),反演計算結果列于表5,n表示迭代次數.

由表5可以看出,空間步長對反演結果的影響很小.

(3)微分階數對反演結果的影響

令初始迭代值a0=(0.3,0.2,0.1),考察時間分數階α,α1,α2的不同取值對反演結果的影響,計算結果見表6,n表示迭代次數.

表6　微分階數對反演結果的影響

通過表6可以看出微分階數對反演結果有一定的影響,隨著微分階數的接近誤差有所增加,并且迭代步數也略微增加.

3.2附加數據有擾動的情形

(1)擾動水平對反演結果的影響仍取微分階數真值a=(0.9,0.7,0.5),數值微分步長τ=0.001,分別取擾動水平δ=1%,0.1%,0.05%,0.01%,20次反演計算的平均值列于表7.

通過表7可以看出隨著數據擾動水平的減小,反演結果精度越來越高.

(2)計算次數對反演結果的影響

表7　擾動水平對反演結果的影響

表8 給定擾動水平下計算次數對反演結果的影響

設擾動水平δ=1%,考察計算次數對反演結果的影響,結果見表8,其中p表示計算次數.

由表8可以看出,對于給定的擾動數據,計算次數對反演結果的影響不大.

4結束語

本文探討了含有三個時間分數階導數的一維反常擴散方程求解及確定微分階數的反問題.正問題的數值模擬結果表明,數值解與解析解吻合較好,所建立的有限差分格式是有效的.對于確定三個微分階數的反問題,雖然理論上還沒有解決反演的穩定性問題,但應用同倫正則化算法可以實現對多個微分階數的數值反演.通過反演計算結果發現,當數據擾動水平較大時,解誤差變得較大.這說明含多個時間分數階導數的反常擴散方程的微分階數反問題具有較高的病態性,其他更有效的反演算法是需要進一步研究的課題.

參考文獻:

[1] 陳文,孫洪廣，力學與工程問題的分數階導數建模[M].北京：科學出版社，2010.

[2] 于強,劉發旺.時間分數階反應-擴散方程的隱式差分近似[J],廈門大學學報:自然科學版, 2006,45(3): 315-319.

[3] 沈淑君.分數階對流-擴散方程的基本解和數值方法[D].廈門：廈門大學, 2008.

[4] Liu F, Meerschaert M M, McGough R J,etal. Numerical methods for solving the multi-term time-fractional wave-diffusion equations[J]. Fractional Calculus and Applied Analysis, 2013, 16: 9-25.

[5] Yury L.Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation[J].Journal of Mathematical Analysis and Applications, 2011, 374:538-548.

[6] Jiang H, Liu F, Turner I,etal. Burrage,Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion equations in a finite domain [J]. Computers and Mathematics with Applications,2012, 64:3 377-3 388.

[7] Cheng J, Nakagawa J, Yamamoto M,etal. Uniqueness in an inverse problem for a one-dimensional fractional diffusion equation [J].Inverse Problems, 2009,25:115 002-115 017.

[8] Liu J J,Yamamoto M,A backward problem for the time-fractional diffusion equation [J], Applicable Analysis, 2010,89:1 769-1 788.

[9] Zheng G H,Wei T.Spetral regularization method for a Cauchy problem of the time fractional advection-dispersion equation [J]. Journal of Computational and Applied Mathematics, 2010, 233:2 631-2 640.

[10] Zheng G H, Wei T.Two regularization methods for solving a Riesz-Feller space-fractional backward diffusion equation [J]. Inverse Problems, 2010, 26:115 017-115 038.

[11] Sakamoto K,Yamamoto M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems [J]. Journal of Mathematical Analysis and Applications, 2011,382:426-447.

[12] Xu X, Cheng J,Yamamoto M.Carleman estimate for a fractional diffusion equation with half order and application [J].Applicable Analysis, 2011,90:1 355-1 371.

[13] Yamamoto M,Zhang Y.Conditional stability in determining a zeroth-order coefficient in a half-order fractional diffusion equation by a Carleman estimate [J].Inverse Problems, 2012,28(10): 105 010-105 019.

[14] Xiong X T, Zhou Q,Hon Y C.An inverse problem for fractional diffusion equation in 2-dimensional case: Stability analysis and regularization [J].Journal of Mathematical Analysis and Applications, 2012,393,185-199.

[15] Li G S, Gu W J, Jia X Z. Numerical inversions for space-dependent diffusion coefficient in the time fractional diffusion equation [J].Journal of Inverse and Ill-Posed Problems, 2012, 20(3): 339-366.

[16] Wei T,Zhang Z Q.Reconstruction of a time-dependent source term in a time-fractional diffusion equation [J]. Engineering Analysis with Boundary Elements, 2013,37:23-31.

[17] Igor Podlubny, Fractional Differential Equations [M].San Diego:Academic press,1999.

(編輯：劉寶江)

Thesolutiontothreetime-fractionalanomalousdiffusion

equationandnumericalinversionofthefractionalorders

SUNChun-long,LIGong-sheng,JIAXian-zheng,DUDian-hu

(SchoolofScience,ShandongUniversityofTechnology,Zibo255049,China)

Abstract:Afinitedifferenceschemeisintroducedtosolvethe1-Dthree-termtime-fractionalanomalousdiffusionequationbasedonCaputo'sdiscretizationtothetimefractionalderivatives.UsingthemethodofseparationofvariablesandLaplacetransform,theanalyticalsolutionoftheforwardproblemisobtained.Furthermore,thehomotopyregularizationalgorithmisappliedtodeterminethethreetime-fractionalordersbytheadditionalmeasurementsataninteriorpointinthedomain.Numericalinversionsareperformedtodemonstrateeffectivenessoftheproposedalgorithm,andinfluencesofthetime-spacemeshgridsandthedatanoisesontheinversionalgorithmarediscussed.

Keywords:timefractionalderivative;threetime-fractionaldiffusion;inverseproblem;homotopyregularizationalgorithm;numericalinversion

中圖分類號：O175

文獻標志碼：A

文章編號：1672-6197(2015)03-0001-07

作者簡介：孫春龍，男，sunchunlong527@163.com; 通信作者： 李功勝，男，ligs@sdut.edu.cn

基金項目：國家自然科學基金資助項目( 11071148, 11371231); 山東省自然科學基金資助項目(ZR2011AQ014)

收稿日期：2014-09-20