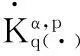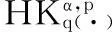變指標Herz型Hardy空間上一類交換子的有界性
王洪彬
(淄博師范高等專科學校 數理科學系, 山東 淄博 255130)
?
變指標Herz型Hardy空間上一類交換子的有界性
王洪彬
(淄博師范高等專科學校 數理科學系, 山東 淄博 255130)
摘要:發展了變指標Herz型Hardy空間理論,應用原子分解定理證明了一類次線性算子和BMO函數生成的交換子在變指標Herz型Hardy空間上的有界性.
關鍵詞:交換子;變指標;Herz型Hardy空間;有界性
在彈性力學、流體力學及其所涉及的偏微分方程研究中,很多情況下需要處理某些具有非標準局部增長條件的問題,其數學表現形式為所謂具有變指標的函數空間問題.1991年,Kovácˇik和Rákosník[1]文章的出現,使得變指標函數空間理論得到了迅速的發展,具有可積性指標的Lebesgue空間和Sobolev空間被廣泛研究[2].之后人們相繼建立了變指標Bessel位勢空間(即廣義變指標Sobolev空間)[3],變指標Triebel-Lizorkin空間[4],變指標Herz空間[5],變指標Hardy空間[6]和變指標Herz型Hardy空間[7],對于調和分析中的重要算子及其交換子在上述空間中的研究也得到了豐富的成果.另外,關于這些空間的許多應用也相繼被人們發現[8].本文應用變指標Herz型Hardy空間中的原子分解定理,證明一類次線性算子和BMO函數生成的交換子在此空間中的有界性.
1預備知識和記號
給定開集Ω?n及可測函數 p(·)∶Ω→[1,∞),Lp(·)(Ω)表示Ω上所有可測函數f的集合,且滿足對某個λ>0,使得∞.
賦予如下Luxemburg-Nakano范數
則Lp(·)(Ω)是Banach空間,稱之為變指標Lebesgue空間.
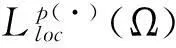
p(·)∶Ω→[1,)的集合, 使得p-=essinf {p(x)∶x∈Ω}>1,p+=esssup {p(x)∶x∈Ω}<.記p′(x)=p(x)/(p(x)-1). 令(Ω)為p(·)∈(Ω)并使得Hardy-Littlewood極大算子M滿足Lp(?)(Ω)有界的指數函數p(·)的集合.


下面我們給出變指標Herz空間的定義. 對于k∈, 令且Ak=BkBk-1. 記+和分別是所有正整數和所有非負整數的集合, 對k∈有χk=χAk, 若k∈+則且其中χAk是Ak的特征函數.
定義 1[5]令α∈, 0 在此基礎上我們給出變指標Herz型Hardy空間的定義及其原子分解特征. 用S(n)表示n上的Schwartz空間, 它是由無窮可微且在無窮遠處迅速遞減的函數所構成的,S′(n)表示S(n)的對偶空間. 令GNf(x)為f(x)的grand極大函數, 其定義為,其中ΑN={φ且是非切向極大算子并且其定義為其中φt(x)=t-nφ(x/t). 定義2[7]令α∈, 0 定義3[7] 令nδ2≤α (ii)n上的函數a被稱為是限制型中心(α,q(·))-原子, 如果它滿足上述條件(b), (c)以及(a)′ 對某個r≥1有suppa?B(0,r). 引理1[7]令nδ2≤α<, 0 其中下確界是對f的所有上述分解而取的. 在主要結論的證明中,我們還需要下面的幾個引理. 其中rp=1+1/p--1/p+. 上述不等式被稱為廣義H?der不等式. 其中δ1,δ2是常數且滿足0<δ1,δ2<1(注意在整篇文章中δ1,δ2都同引理3中的一樣). 2主要結論及證明 定理1 令nδ2≤α<,0 [b,T]f滿足尺寸條件 (1) 我們首先估計I1. 由式(1)和廣義H?der不等式得 所以由引理2~5, 有 ‖[b,T](aj)χk‖Lq(·)(n)≤C2-k(n+s+δ)2j(s+δ-α){‖(b-bBj)χk‖Lq(·)(n)‖χBj‖Lq′(·)(n)+ ‖(bBj-b)χj‖Lq′(·)(n)‖χk‖Lq(·)(n)}≤C2-k(n+s+δ)2j(s+δ-α){‖b‖*‖χBk‖Lq(·)(n)‖χBj‖Lq′(·)(n)+ (k-j)‖b‖*‖χBj‖Lq′(·)(n)‖χBk‖Lq(·)(n)}≤C2-k(n+s+δ)2j(s+δ-α)(k-j)‖b‖*‖χBk‖Lq(·)(n)‖χBj‖Lq′(·)(n)≤ (2) 因此, 當0 (3) (4) 現在來估計I2. 類似地, 我們考慮p的兩種情形. 當0 (5) (6) 因此, 定理得證. 參考文獻: [1] Kovácik O, Rákosník J. On spaces Lp(x)and Wk,p(x)[J]. Czechoslovak Math J, 1991, 41(4): 592-618. [2] Diening L, Harjulehto P, H?st? P,etal. Lebesgue and Sobolev spaces with variable Exponents[M]. Heidelberg:springer, 2011. [3] Diening L. Riesz potential and Sobolev embeddings of generalized Lebesgue and Soblev spaces Lp(·)and Wk, p(·)[J]. Math Nachr, 2004, 268(1): 31-43. [4]Xu J S. Variable Besov and Triebel-Lizorkin spaces[J]. Ann Acad Sci Fenn Math, 2008, 33:511-522. [5] Izuki M. Boundedness of sublinear operators on Herz spaces with variable exponent and application to wavelet characterization[J]. Anal Math, 2010, 36(1):33-50. [6] Nakai E, Sawano Y. Hardy spaces with variable exponents and generalized Campanato spaces[J]. J Funct Anal, 2012, 262(9):3 665-3 748. [7]Wang H B, Liu Z Z. The Herz-type Hardy spaces with variable exponent and their applications[J]. Taiwanese J Math, 2012, 16(4):1 363-1 389. [9] Izuki M. Boundedness of commutators on Herz spaces with variable exponent[J]. Rend del Circolo Mate di Palermo, 2010, 59(2):199-213. (編輯:郝秀清) BoundednessofcommutatorsonHerz-typeHardyspaceswithvariableexponent WANGHong-bin (DepartmentofMathematicalandPhysicalScience,ZiboNormalCollege,Zibo255130,China) Abstract:Usingtheatomicdecompositiontheorem,weobtaintheboundednessofthecommutatorsgeneratedbyaclassofsublinearoperatorsandtheBMOfunctionsontheHerz-typeHardyspaceswithvariableexponent. Keywords:commutator;variableexponent;Herz-typeHardyspace;boundedness 中圖分類號:O174.2 文獻標志碼:A 文章編號:1672-6197(2015)03-0027-05 作者簡介:王洪彬, 男,hbwang_2006@163.com 基金項目:國家自然科學基金資助項目(11171345); 淄博師范高等專科學校研究課題(13xk023) 收稿日期:2014-10-15