基于牛頓插值算法的二維PSD非線性校正

李　倩, 李田澤， 解愛章

(1.山東理工大學 電氣與電子工程學院， 山東 淄博 255049；

2.淄博機電工程學院， 山東 淄博 255300)

?

基于牛頓插值算法的二維PSD非線性校正

李倩1, 李田澤1， 解愛章2

(1.山東理工大學 電氣與電子工程學院， 山東 淄博 255049；

2.淄博機電工程學院， 山東 淄博 255300)

摘要：為了提高位置敏感探測器(PSD)的測量精度，減少其非線性帶來的誤差，提出了基于牛頓插值算法的非線性補償插值算法.這種新型算法是通過逐次生成插值多項式的算法，當插值節點增減時，只要增加或減少一項即可，可以節省算術運算的次數，極大地簡化了運算.實驗結果證明，對比雙二次線性插值算法的線性校正數據及插值誤差分析，該算法的非線性校正精度更高、插值誤差較小.

關鍵詞：位置敏感探測器PSD； 牛頓插值算法； 插值誤差分析； 非線性

光電位置敏感探測器(PSD)基于橫向光電效應，它具有響應速度快、靈敏度高、頻譜響應寬、處理電路簡單等獨特的優點，被廣泛應用于光電檢測等領域[1].

但是PSD的非線性使得整個器件所測數據置信度下降,盡管有些改進型PSD線性度得以改善，但其非線性仍不可避免.雖然在中央區域線性度很好，但PSD的非線性嚴重制約邊緣區域的準確度，如何解決它已成為非常棘手的問題.目前主要采用的插值校正算法有雙一次插值、雙二次插值等方法，而大多數研究都在理論研究階段，給出實際測試數據的資料不多，并且當插值節點增減時，計算要全部重新進行，為了計算方便本文提出基于牛頓插值算法的二維PSD非線性校正.

1 PSD工作原理

當入射光點落在PSD感光面的不同位置時，將對應輸出不同的電信號，通過對此輸出電信號的處理，即可確定入射光點在器件感光面上的位置.PSD可以分為一維PSD和二維PSD，一維是在線型的PSD兩端位置引出兩個電極；二維PSD是在光敏面的兩邊對邊上的幾何中心點位置引出四個收集光電流的電極[2-3].

一維PSD電流與光點位置方程：

(1)

(2)

式中:I1、I2分別為兩個電極的輸出光電流;I0為總的光電流;x是光斑能量中心的坐標;L為PSD中點到信號兩級間的距離.

二維PSD電流與光電位置方程：

(3)

(4)

式中:Ix1、Ix2和Iy1、Iy2分別為各電極的輸出光電流，x,y是光斑能量中心的坐標，L為PSD中點到信號兩級間的距離.

2雙二次線性插值算法

文獻[4]中介紹了雙一次線性插值和雙二次線性插值的方法，并且證明了雙二次線性插值算法的校正精度和準確度高于雙一次線性插值算法.下面簡單介紹雙二次插值算法.

給定任意一個測量點p(x,y),該點的補償值Ex(x,y),Ey(x,y)可以用包含該點的一個田字補償網格A1A2A3A4A5A6A7A8A8A9上的9個頂點的補償值Ex(xi)，Ey(yi)的線性組合來表示(以x為例，y向同)，即

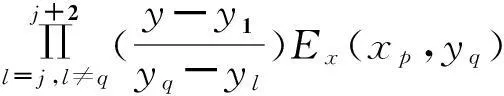
(5)

(6)

稱

為系數函數[5].

如果實測網格式均勻的，那么補償網格的9個頂點的坐標可以用兩個一維矩陣表示：x=[x1,x2,x3]，y=[y1,y2,y3]。系數函數φ(p,q,k,l)是由這6個坐標值x1,x2,x3,y1,y2,y3確定的函數.

3牛頓插值算法

牛頓插值算法是利用函數f(x)在某區間中若干點的函數值，做出適當的特定函數，在這些點上用這特定函數的值作出函數f(x)近似值.如果這特定函數式是多項式就稱它為牛頓插值多項式.

牛頓插值多項式是基于差商所構造的插值多項式，它與雙一次線性、雙二次線性插值多項式本質上是一樣的，只是表現形式不同.當插值節點增減時，雙二次線性插值算法要全部重新進行，而牛頓插值算法計算方便，且增加節點時，只要增加一項即可，簡化了運算[6-7].

n+1個節點xi(i=0,1,2,…，n)牛頓插值多項式為

f(x)=f(x0)+f[x0,x1](x-x0)+

f[x0,x1,x2](x-x0)(x-x1)+…+

f[x0,x1,…，xn](x-x0)(x-x1)…

(x-xn-1)

(7)

記

f[x0,x1,…，xi]

(8)

Nn(x)是f(x)的n次插值多項式，稱為牛頓插值多項式，又可寫為

Nn(x)=Nn-1(x)+

(9)

一階差商：

(10)

二階差商：

(11)

N階差商：

f[x0,x1，…,xn]=

(12)

4 實驗驗證

4.1在線數據采集裝置

為了驗證上述兩種算法哪一種的非線性補償性更好，本文選取了一塊日本HAMAMATSU公司產的S1880進行實驗，實驗步驟如下：

第一步，誤差離散化.由于PSD的非線性誤差在x,y方向上相對獨立，故對每一點對應的由x方向位置誤差函數Ex(x,y),y方向的位置誤差函數Ey(x,y);不過，在此只選擇Ex(x,y)為例，進行推導，因Ey(x,y)的推導完全類同.為了得到誤差函數，將PSD置于一高準確度數控位移平臺上，固定一激光器使其照射在PSD敏感面上，則控制一定步長S沿x,y方向改進，即可得到一系列網格點陣上的誤差函數值Ex(xi,yi),Ey(xi,yi)[8]

(13)

式中(xc,yc)為PSD網格點的測量值，(xtc,ytc)為三坐標測量機的準確位置讀數.

第二步，查找網格點，判斷待修正的點與網格上哪個點距離最近，把最近的網格點作為補償網格的中心點.

第三步，按照牛頓插值算法的思想，給定任意一個測量點p(x,y),該點的補償值Ex(x,y),Ey(x,y)對照式(7)進行誤差修正，只要是在網格內任意一點，就可以得到修正后的坐標.

4.2 兩種插值算法線性校正數據比較

表1給出了兩種算法對同一組測量值的校正結果.第10組、第20組數據的x坐標補償結果相差最大，分別相差8μm和13μm.

由表1中兩種算法校正數據可看出，牛頓插值算法校正后的數據與三坐標測量機的讀數相差大部分小于2μm，而雙二次線性插值算法與三坐標測量機的讀數相差很大.由此得知，牛頓插值算法比雙二次線性插值算法校正精度更高.

4.3 兩種插值誤差分析比較

對雙二次插值算法，其插值誤差：

Rn(x,y)=

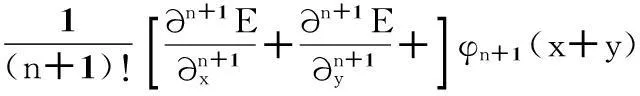
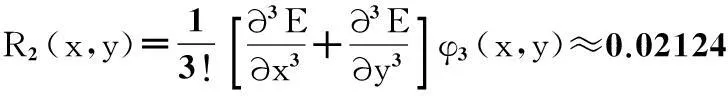
(14)　取n=2,則

對牛頓插值算法，其插值誤差：

Rn(x,y)=f(x,y)-pn(x,y)

=f[(x,y),(x0,y0);…;(xn,yn)]wn+1(x,y)

(16)

式中，

wn+1(x,y)=

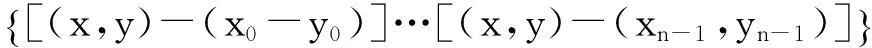
如圖1所示計算流程如下：

程序開始，存放一階差商f[(x0,y0),(x1,y1)]，f[(x0,y0),(x1,y1)]，f[(xi-1,yi-1),(xi,yi)]…f[(xn-1,yn-1),(xn,yn)],n=0,1,…，i. 是一階差商數組.第一步外層循環，循環變量j，表示計算第j階差商值，設循環變量初值為1，終值為n；第二步內層循環，循環變量i，表示同階差商計算n次，設循環變量初值為n，終值為j.取n=2，求得插值多項誤差R2(x,y)為

R2(x,y)=f(x,y)-p2(x,y)=

f[(x,y),(x0,y0),(x1,y1),(x2,y2)]w3(x,y)=

f[(x,y),(x0,y0),(x1,y1)(x2,y2)]·

{[(x,y)-(x0,y0)][(x,y)-(x1,y1)]}≈

0.01532

(17)

圖1 插值誤差計算程序框圖

由式(15)、式(17)得出牛頓插值誤差比雙二次性插值誤差小，線性補償能力較好.

5 結束語

PSD為一種高靈敏度,高準確度位置敏感探測器，如何克服非線性帶來的影響，是測量領域關心的重要問題.本文提出的基于牛頓插值算法的PSD非線性校正算法，對比雙二次線性插值算法的線性校正數據及插值誤差分析補償精度更高、插值誤差較小.故在不增加成本，不改變測量設備復雜度的情況下，擴大了測量范圍，提高了PSD的利用價值.

參考文獻：

[1]黃烈云，莫彥袆，向勇軍. 大面積枕型二維位敏探測器的研制[J]. 半導體光電，2014,35(2)：211-213.

[2]閆洪猛，李田澤，劉坤. 二維PSD非線性誤差修正算法的研究[J]. 山東理工大學學報(自然科學版)，2007,21(6):31-34.

[3]張鳳奇，王永生，張寶尚，等. 二維位置敏感器件(PSD)的畸變校正算法研究[J]. 計算機科學，2013，40(11A):150-152.

[4]叢培田，劉廣軍，陸明. 探測器(PSD)的非線性補償技術[J]. 儀表技術與傳感器， 2012，7: 53-57.

[5]管炳良，李星，王俊. 二維PSD非線性修正技術研究[J]. 儀器儀表學報，2007，28(7)：1295-1298.

[6]范開國，楊建國，姚曉棟，等. 基于牛頓插值的批量軸類零件加工誤差補償[J]. 機械工程學報，2011,47(9)：112-116.

[7]李慶揚，王能超，易大義. 數值分析[M]. 北京：清華大學出版社，2008.

[8]ClarenceO.E.Burg.Derivative-basedclosedNewton-cotesnumericalquadrature[J].AppliedMathematicsandComputation,2012,218(13):7052-7065.

(編輯：劉寶江)

Two dimensional PSD nonlinear modified Newton interpolation algorithm

LI Qian1， LI Tian-ze1, XIE Ai-zhang2

(1.School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255049, China；

2.Zibo Electrical and Mechanical Engineering， Zibo 255300, China)

Abstract:In order to improve the position sensitive detector(PSD) measurement accuracy, reduce the nonlinear error caused by the online data acquisition, a nonlinear compensation algorithm based on Newton interpolation algorithm is proposed.This algorithm uses micro displacement platform and correction device and is based on difference polynomial algorithm.It can increase or decvease the number to save the arithmetic operation, and simplify the computation. Experimental results show that compared with two linear interpolation algorithm and the interpolation error correction data analysis, the nonlinear compensation precision of this algorithm is higher, and the interpolation error is smaller.

Key words:position sensitive detector PSD; Newton interpolation algorithm; the interpolation error analysis; annealing

中圖分類號：TN929

文獻標志碼：A

文章編號：1672-6197(2015)03-0069-04

作者簡介：李倩，女，Liqianll2@163.com; 通信作者： 李田澤，男，Ltzwang@163.com

基金項目：山東省自然科學基金資助項目(ZR2012FL19)

收稿日期：2014-09-12