列車運行引起的CFG樁復合路基動力響應分析

高廣運， 李紹毅

(1.同濟大學 地下建筑與工程系，上海　200092； 2. 同濟大學 巖土及地下工程教育部重點實驗室，上海　200092)

?

列車運行引起的CFG樁復合路基動力響應分析

高廣運1,2， 李紹毅1,2

(1.同濟大學 地下建筑與工程系，上海200092； 2. 同濟大學 巖土及地下工程教育部重點實驗室，上海200092)

隨著列車速度的不斷提高，列車運行引起的地面振動對沿線環境的影響受到廣泛關注。高速列車運行對臨近建筑物的安全性、工作環境的舒適性和精密儀器和設備的正常運行有很大影響[1]。針對高速列車運行產生的環境振動問題早期有Eason[2]、Metrikine等[3]、Dinkel等[4]的研究論文，討論了移動點荷載作用于彈性梁板上或均質地基上的動力響應，分析了振動波的傳播和臨界速度。

解析法或半解析法適用于簡化模型，有限元方法可以模擬復雜路基。2.5維有限元方法采用傅里葉變換將三維有限元模型轉化為二維有限元模型，大大減少了數值模型的計算量和計算時間。Yang等[5]采用2.5維有限元方法研究了半無限彈性土體的列車動力響應。邊學成等[6]采用2.5維有限元分析了列車荷載作用下軌道結構-地基的動力響應。Gao等[7]采用2.5維有限元方法分析了移動荷載作用下飽和分層路基的地面振動。

列車運行引起的地面振動與地基土分層和力學性能有很大關系。Kouroussis等[8]采用分步模型研究了脈沖荷載和列車荷載作用下不同土體參數和分層路基的地面振動，發現土體分層對地面振動有較大影響。李佳等[9]采用2.5維有限元研究了橫觀各向同性路基動力響應，發現應力波在軟土層中傳播所消耗的能量大于硬土層。

為了控制高速鐵路軟土地基的工后沉降，復合路基技術被采用。復合路基提高了地基承載力[10]，改善了軟土路基的力學性能，復合路基地面振動與天然地基有差異。Thach等[11]采用有限元建立了PCC樁加固路基的振動分析模型，對比了天然路基與加固路基振動響應，發現采用PCC樁加固后路基振動減小。Thach等[12]采用ABAQUS建立了列車荷載作用下樁體加固路基動力分析模型，發現隨車速提高列車荷載模式與軌道位移模式差異增大；路堤和地基加固體對高頻振動有較強吸收作用，減小了遠離路堤的地面振動。

王維玉等[13]通過現場試驗研究了天然地基和CFG樁復合地基動力特性和時程響應，發現CFG樁復合路基增加了天然地基剛度。屈暢姿等[14]通過現場實測和小波分析討論了CFG復合路基的地面振動，發現隨著車速提高軌道不平順成為引起路基振動的主要原因。劉麗萍等[15]將復合地基視為橫觀各向同性材料，利用半解析數值方法分析板-復合地基動力相互作用，發現增大加固深度、置換率和樁土模量比對系統頻率和振幅均有影響。康文生[16]利用有限元軟件MIDAS/GTS，建立了灰土樁復合地基和天然黃土地基上鐵路路基的三維有限元模型，發現復合地基的動應力大于天然地基。韓海燕[17]采用等效復合土層模擬水泥土攪拌樁路基，分析列車作用下復合路基的地面振動，發現復合路基減小了加固區附近地面振動，提高了軌道結構的動力穩定性。

上述研究表明復合路基相對于天然路基的力學性能有很大改善，路基動力響應較加固前不同。CFG樁加固后列車運行引起的地面振動衰減規律和振動頻譜變化尚需詳細研究，CFG復合路基對地面振動的影響機理還有待討論。對此，本文采用美國軌道功率譜和非線性輪軌接觸Hertzian公式描述鋼軌，結合多質點列車模型建立了列車-軌道模型，采用2.5維有限元方法建立了CFG樁復合路基模型，分析了CFG樁復合路基對鐵路路基及沿線地面振動的影響。

1列車-軌道-路基模型

1.1列車模型

采用多質點模型模擬列車荷載，模型示意圖如圖1。列車車廂、轉向架和車輪分別采用質點模擬，列車的一、二級懸掛系統采用彈簧和阻尼器模擬。根據質點豎向動力平衡方程，多質點模型動力方程可以表示為：

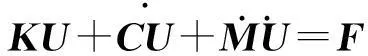
(1)

式中：K,C,M為模型的剛度矩陣、阻尼矩陣和質量矩陣；U為模型位移矩陣；F為模型外力矩陣。

多質點模型中的質點質量、彈簧剛度和阻尼系數代入方程(1)，得到三質點模型的動力方程：

(2)

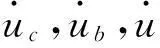
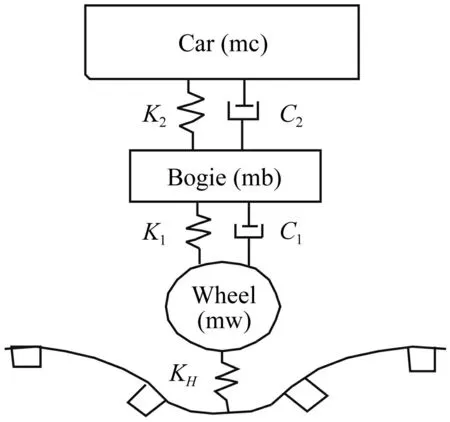
圖1　列車模型 Fig.1 The model of train

方程(2)中列車的輪軌作用力Fwr未知，根據車輪與鋼軌的輪軌接觸模型確定輪軌作用力。通過輪軌接觸模型建立軌道模型與列車模型的聯系，聯立車輛和軌道模型求得輪軌作用力。

1.2軌道模型

1.2.1輪軌接觸模型

現有輪軌接觸模型分為彈簧模型和Hertzian非線性模型。Hertzian非線性公式考慮了輪軌作用力的非線性變化和輪軌脫開，較彈簧模型更為合理[18]，如下：

Fwr=kH(uw-ur-r)1.5,當uw-(ur+r)<0

(3a)

Fwr=0, 當uw-(ur+r)>0

(3b)

式中：ur為車輪作用下輪軌接觸點處的鋼軌豎向位移；r為鋼軌的初始不平順幅值；kH為輪軌接觸剛度系數。

Hertzian公式中列車的輪軌接觸力為輪軌相對位移的函數。輪軌相對位移大于0時，車輪與鋼軌脫開，輪軌接觸力等于0；輪軌相對位移小于0時，車輪與鋼軌接觸，輪軌接觸力為輪軌相對位移的非線性函數。

1.2.2鋼軌模型

鋼軌模型如圖2所示，鋼軌采用鋪設在路基上的Euler梁模擬，軌枕采用彈簧和阻尼器模擬。

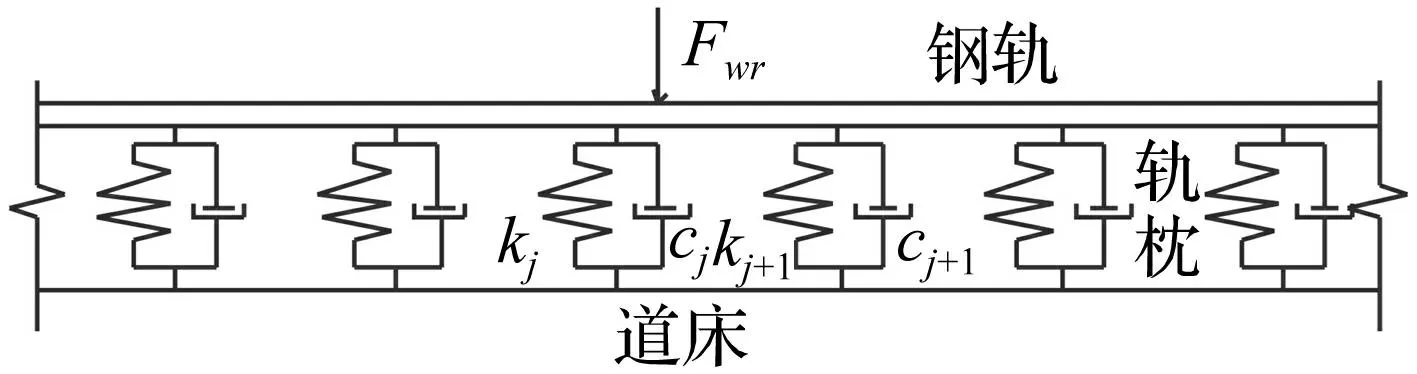
圖2　鋼軌-軌枕模型圖Fig.2 The model of track and sleepers

采用Euler梁模擬鋼軌，單個移動荷載作用梁上時簡支梁的動力方程為：

(4)

式中：ur(x,t)為鋼軌豎向位移；EI為鋼軌剛度；m為鋼軌單位長度質量；c為鋼軌阻尼；P(t)為移動荷載；δ(x-Vt)為迪克拉函數。式(4)中右邊表示只有當x=Vt時梁上有荷載P(t)作用。

采用彈簧和阻尼器模擬軌枕作用，連續鋼軌軌枕處作用反力為鋼軌位移和速度的函數，將軌枕對鋼軌的作用反力視為作用位置不隨時間變化的外荷載，采用受多外力作用簡支梁動力模型模擬多跨連續鋼軌，簡支梁動力方程采用振型分解法求解[19]。

M個軌道軌枕作用，振型數目取N，振型分解法控制方程的矩陣表達式為：

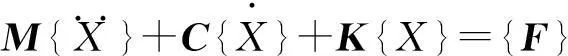
(5)

{M}為廣義質量矩陣

{K}為廣義剛度矩：

{K}=

{F}為廣義力向量：

1.2.3鋼軌初始不平順

采用美國功率譜描述鋼軌初始不平順幅值。美國軌道功率譜為美國聯邦鐵路管理局根據測量得到的軌道幾何參數數據庫，采用截斷頻率和粗糙度常數表示，用于描述軌道不平順的功率譜密度函數[18]。按軌道不平順程度美國功率譜分為6級，其中軌道不平順類型又分為高低不平順、方向不平順、水平不平順和軌距不平順。

本文僅考慮軌道高低不平順，軌道的高低不平順功率譜Sk(ω0)計算公式如下：

(6)

式中：ω0為軌道不平順空間頻率；ωc為高低不平順截斷頻率；Av為高低不平順程度的參數；k為安全系數，取值范圍為0.25~1.0。

根據離散傅里葉變換理論，采用時間序列估計功率譜密度的Blackman-Turkey周期圖法，求得軌道不平順空間域內的模擬序列見圖3。

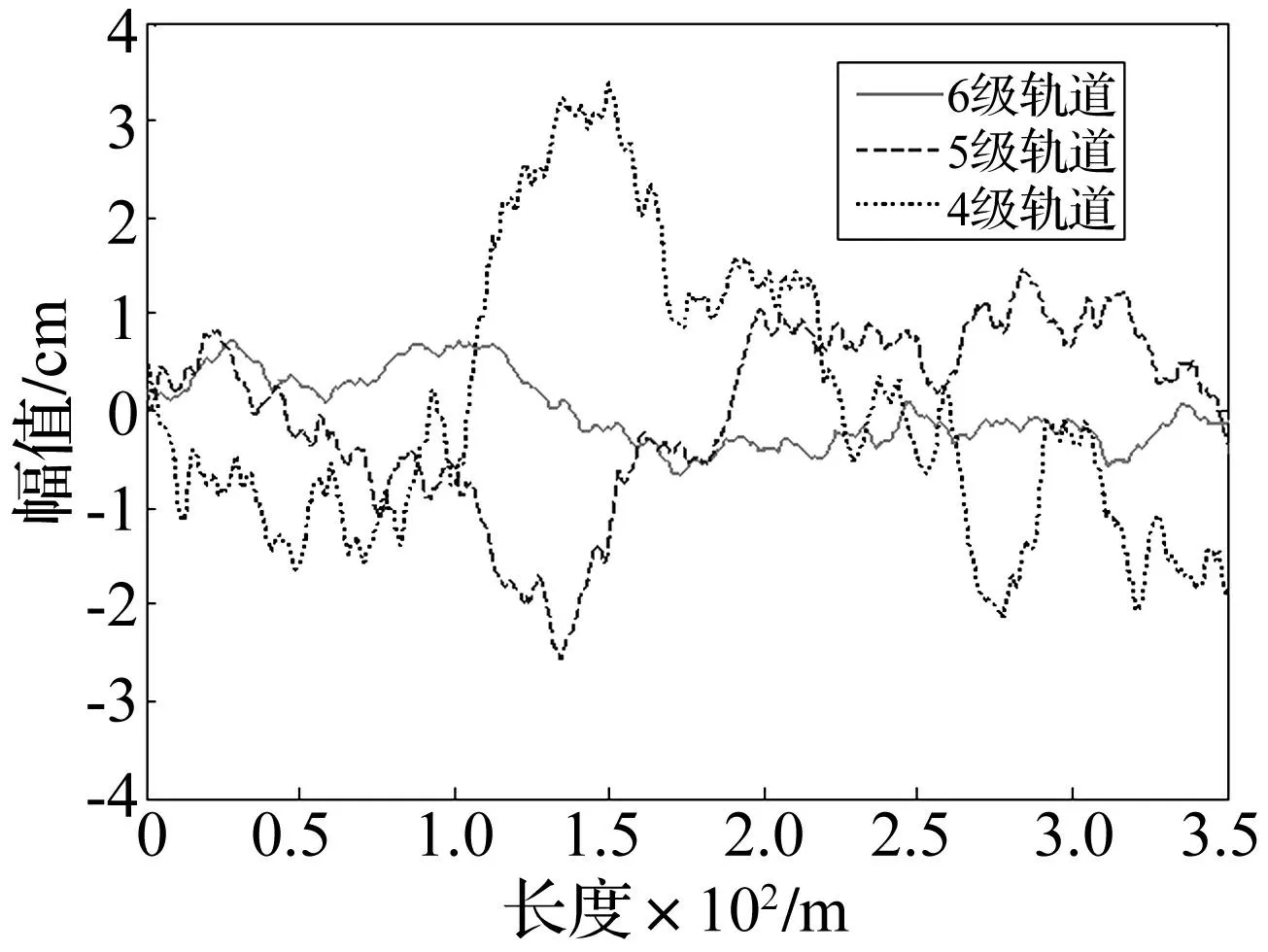
圖3　鋼軌不平順幅值圖Fig.3 The amplitude of the irregularity of track

1.3路基模型

1.3.12.5維有限元模型

路基采用有限元方法建模，將輪軌作用力加載于路基模型中的軌道上，采用2.5維有限元求解路基動力響應。假定軌道和路基在列車的運行方向上材料性質和空間分布為連續均勻，將三維路基有限元模型在列車運行方向上進行波數分解，在時間域上進行傅里葉變換，路基三維動力響應問題轉換為二維問題。2.5維有限元模型如圖4。

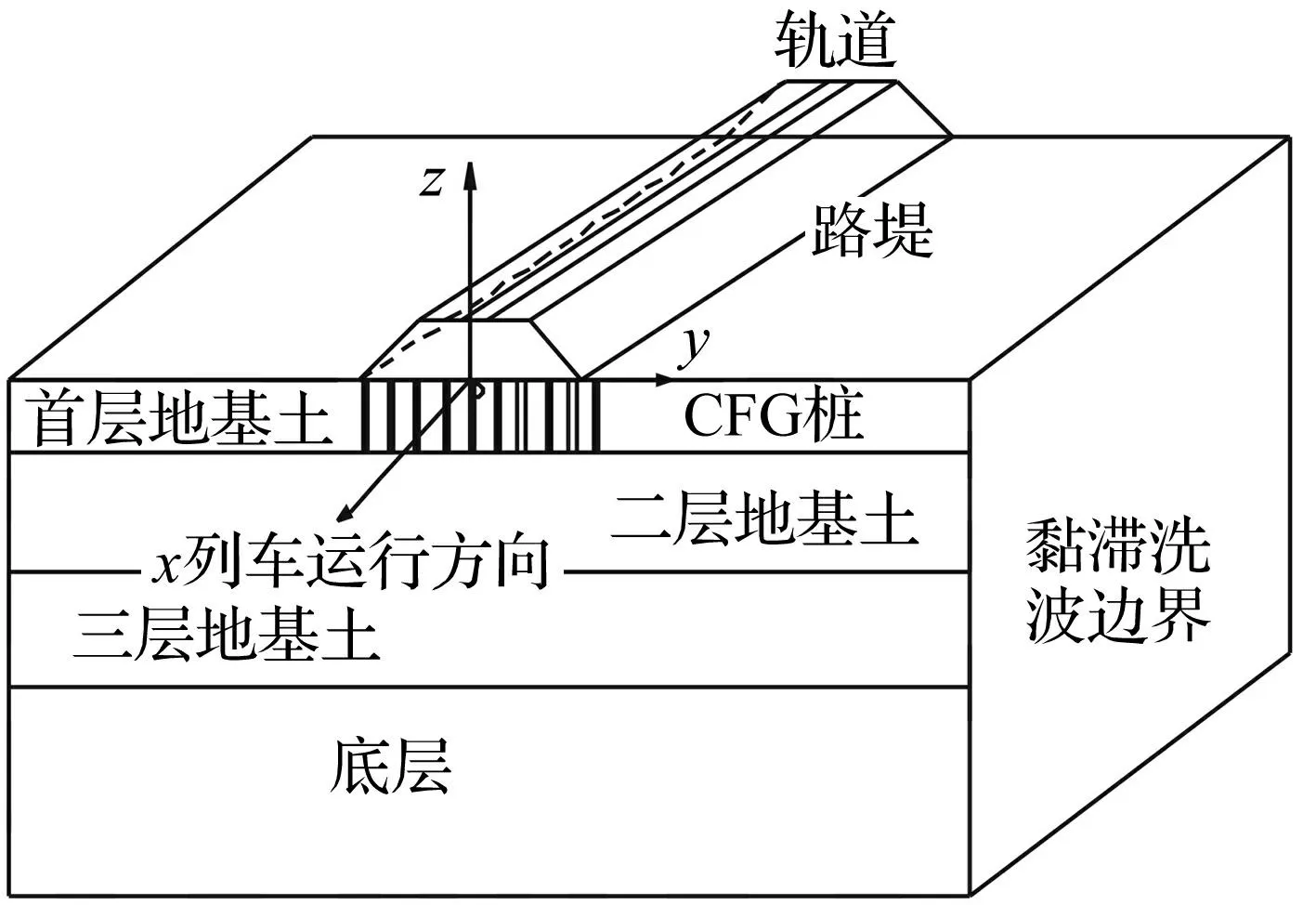
圖4　路基有限元模型示意圖Fig.4 The FE model of railway subgrade

路基三維有限元模型中節點位移為u(x,y,z,t)，采用波數分解、時間域的傅里葉變換可得到頻率域和波數域模型的節點位移表達式：

(7)

由方程(7)可將三維列車-路基動力有限元模型轉換為二維模型求解，然后通過傅里葉逆變換：

u(x,y,z,t)=

(8)

可以得到三維時間域-空間域內列車荷載作用下路基振動的有限元解答。

采用考慮土體阻尼系數的復數形式Lame常數推導2.5維有限元控制方程，Lame常數表達式為：

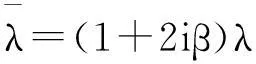
(9a)

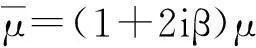
(9b)

采用傅里葉變換處理Navier方程，路基三維有限元動力方程在頻域內表達式為：

(10)

采用虛功原理[6]可以推導出2.5維有限元控制方程為：

(K-ω2M)U=F

(11)

式中：K、M、F分別為總體剛度矩陣，質量矩陣和外力矢量；

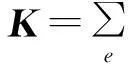
(12)

(13)

(14)

式中：“*”表示共軛矩陣；N為有限元形函數；η、ξ為單元局部坐標；J為雅可比矩陣；D為應力矩陣；B為偏導矩陣。其中應力矩陣和偏導矩陣為：

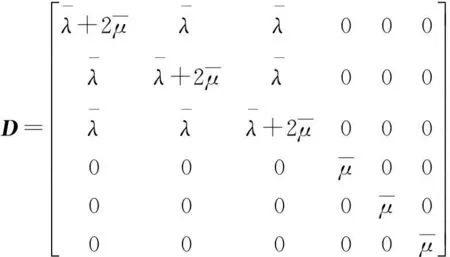
1.3.2有限元模型中軌道模型

2.5維有限元路基模型中采用Euler梁建立軌道模型，將輪軌作用力Fwr作用在路基模型中的歐拉梁軌道上，路基模型中歐拉梁動力方程為[6]：

fIT(x,t)+δ(x-Vt)Fwr(t)

(15)

式中：fIT(x,t)為軌道-路基接觸點反力。

采用時間域傅里葉變換和波數展開處理方程(15)，2.5維有限元中軌道動力方程為：

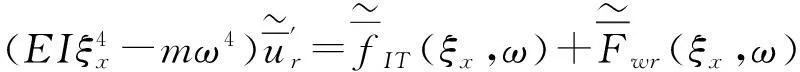
(16)

1.3.3CFG樁墻模型

2.5維有限元模型中離散CFG樁在列車運行方向上簡化為樁墻建模，樁墻的等代彈性模量通過縱向面積置換率計算，樁的橫向間距及斷面尺寸不變。樁墻等代彈性模量計算如下：

(17)

式中：Esp為樁墻的彈性模量；Ep為樁體彈性模量；Es為土體彈性模量；l為樁中心間距；D為CFG樁直徑。

1.3.4黏滯吸波邊界

為減小有限元邊界反射波對有限元模型動力分析的影響，模型邊界采用黏滯阻尼吸波邊界條[20]，黏滯阻尼吸波邊界表達式如式(18)：

(18)

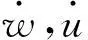
2有限元模型驗證

瑞典國家鐵路局對X2000列車進行了詳盡的現場測試，為列車路基振動研究提供了豐富實測數據。采用X2000列車運行的實測振動數據驗證本文有限元計算模型。根據瑞典X2000列車實測地層、路堤參數和列車軸重參數[6]，采用本文2.5維有限元模型，計算列車以70 km/h和200 km/h運行時的振幅時程曲線與實測結果對比，如圖5。本文2.5維有限元計算模型能較好模擬地面振幅隨時間的變化，各時間點處路基振動趨勢與實測結果一致，圖示表明車速接近地基臨界波速時路基振動的急劇增大[6]，表明本文2.5維有限元路基模型能夠有效模擬列車運行引起的路基振動。

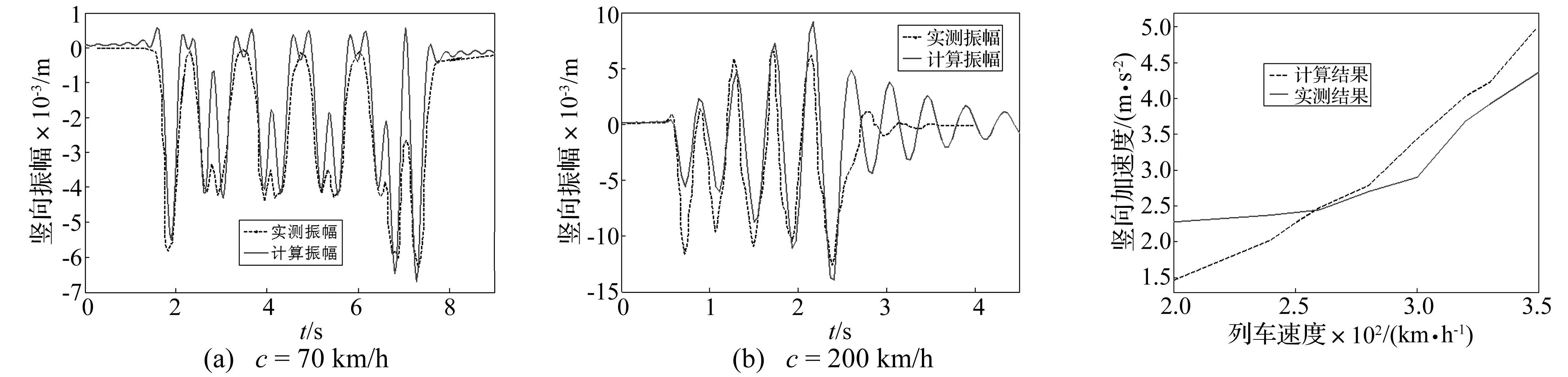
圖5 不同列車速度軌道中心處路基振動響應時程曲線Fig.5Thevibrationattrackcenterfordifferenttrainspeeds圖6 路堤面加速度變化實測結果與計算對比Fig.6Thecomparisonofembankmentvibrationtestvalueandnumericalone

不同列車運行速度下，武廣高速鐵路CFG樁加固路基的地面振動加速度實測數據見文獻[14]。文獻[14]實測數據與本文2.5維有限元模型計算結果對比如圖6，可以發現本文2.5維有限元模型能夠較好模擬CFG樁復合路基路堤面振動加速度隨列車運行速度的變化。

3CFG樁加固路基振動計算

列車模型采用CRH系列高速列車參數[21]，CRH列車質點模型參數如表1。鋼軌不平順等級取美6級，鋼軌單位長度質量取60 kg/m，鋼軌剛度系數取EI=6.42×106Nm2，輪軌接觸剛度取KH=9.4×1010N/m1.5[22]，軌道下軌枕彈簧阻尼模型剛度和阻尼系數分別取33×106N/m和49×103Ns/m。復合路基材料參數采用京滬高速鐵路軟土地區徐滬段的地層參數和CFG樁復合地基參數[23]，土層和路基的參數如表2。

表1　列車模型參數[21]

樁網結構CFG復合路基如圖7。路堤高度4.15 m，基床表層厚0.4 m，碎石墊層厚0.6 m，墊層內鋪設一層土工格柵，CFG樁為直徑0.5 m端承樁，樁間距1.8 m，持力層為強風化角閃巖。地層分布自上而下依次為層硬塑黏土(6 m)和2層強風化角閃巖。CFG樁復合路基材料參數如表2。2.5維有限元模型中碎石墊層上土工格柵的彈性模量取碎石墊層彈性模量的1.4倍[23]，改變泊松比以模擬土工格柵對側向變形的影響。

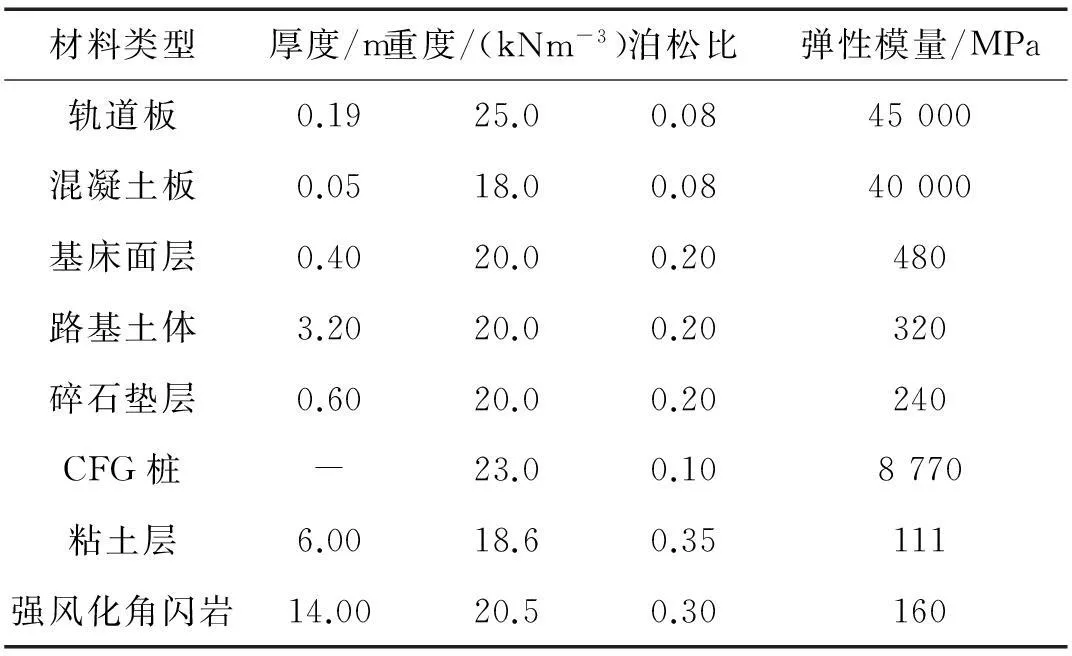
表2　CFG樁復合路基材料計算參數[23]

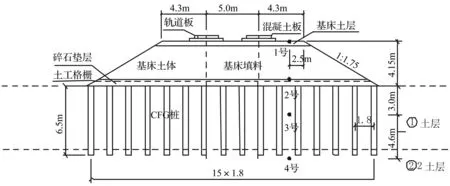
圖7　復合路基橫斷面圖Fig.7 The cross section of composite subgrade

圖8為列車運行速度為150 km/h時，距軌道中心2 m處路堤面振動速度時程和頻譜曲線圖。由圖可知，地面振動頻譜曲線有多個峰值，列車引起地面振動的頻譜峰值可用式(19)計算[18]：

(19)

式中：v0為列車速度；Lb為作用間距。列車車廂轉向架間距18.7 m，運行速度為150 km/h時fb,1為2.2 Hz，車廂軸重引起頻率2.2 Hz的低頻振動。由式(19)可得間距0.6 m軌枕產生頻率為70 Hz的振動，對應頻譜圖8(b)中70 Hz的振動頻譜峰值，軌枕間距對列車引起的地面振動有一定影響。

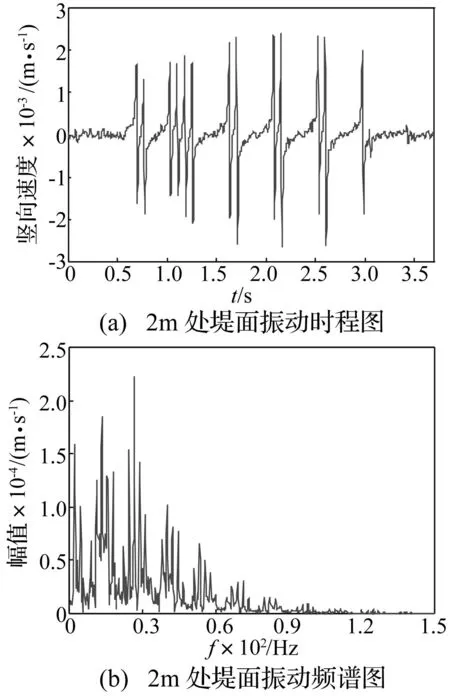
圖8　距軌道中心2 m堤面振動時程圖和頻譜圖Fig.8 Embankment vibration at 2 m away from the track center in time and frequency domain

圖9為路堤和路基中不同深度處振動速度的功率譜密度曲線，計算點位如圖7所示，1號點位于路堤面，2號點位于路堤底部(CFG樁碎石墊層頂面)，3號點位于CFG樁間(CFG樁碎石墊層底面下3.0 m處)，4號點位于CFG樁端下。如圖9(a)所示不同觀察點CFG復合路基與天然路基振動差異頻段不同，1號點處振動明顯差異頻段為1~20 Hz；2號點處振動明顯差異頻段為1~50 Hz和高于60 Hz。CFG復合路基對路堤面振動的影響與對路堤底振動的影響不同。圖9(b)示，與天然路基相比，CFG復合路基對3號點處振動功率譜值有較大影響，CFG樁間土振動譜值有明顯降低；復合路基對4號點處振動譜值影響較小，CFG樁端下土體振動譜值減小較小。文獻[24]指出路堤對列車引起振動有波導作用，即路堤邊坡對振動波有反射和耗散作用，從而減小路堤外的地基振動。CFG樁體對振動波的影響與路堤類似[12]，路基中的振動波，特別是高頻振動在CFG樁間不斷耗散，導致CFG樁間土振動譜值降低。CFG樁端下由于沒有CFG樁體的波導作用，振動譜值與天然路基差異較小。

4復合路基振動衰減分析

CFG樁體對高頻振動有波導作用，可明顯減小CFG復合路基地面高頻振動。本節分析CFG復合路基對路堤面以及路堤外地面振動速度的影響。

圖10為車速為150 km/h時，距離軌道2 m處和4 m處路堤面振動速度功率譜密度。由圖可知，CFG樁復合路基加固后，距離軌道2 m處路堤面小于20 Hz和高于125 Hz的振動譜值下降；距軌道4 m處路堤面小于25 Hz和高于75 Hz的振動譜值下降。相比距軌道2 m處路堤面振動，CFG復合路基對路堤邊緣(4 m處)的振動明顯減小，路堤邊緣高頻振動功率譜值的降低幅度也較大。與文獻[12]和[17]的結論一致，CFG樁復合路基可明顯減小路堤面振動，有利于路堤穩定。究其原因復合路基對路堤邊緣的高頻振動減小較大，降低了路堤邊緣振動速度，提高了路堤邊緣的穩定性。

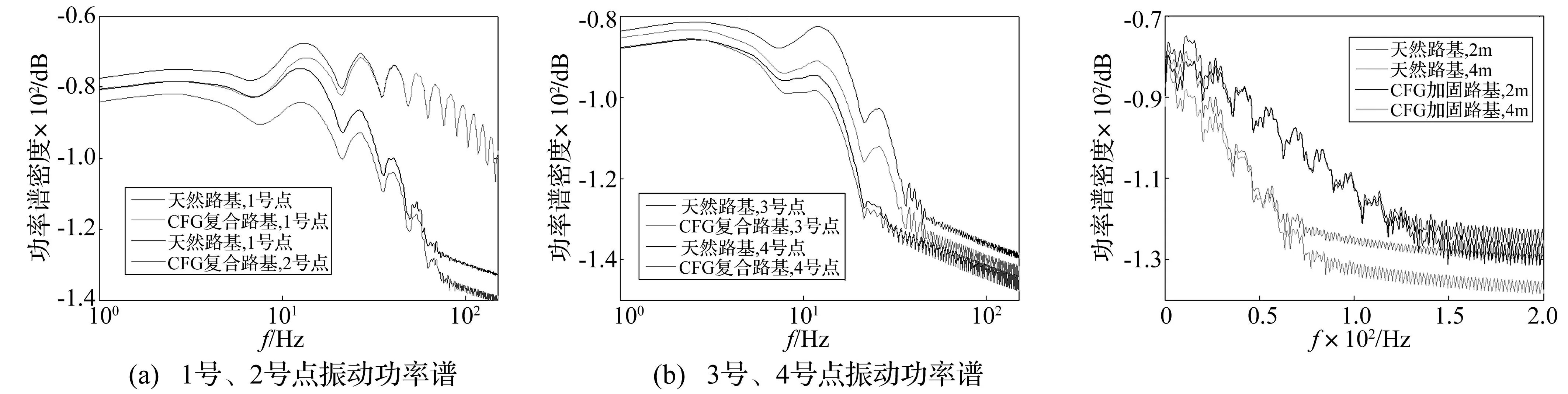
圖9 CFG復合路基和天然路基的振動功率譜密度Fig.9ThePSDofthevibrationforbothCFGcompositesubgradeandnaturalsubgrade圖10 列車速度150km/h路堤面振動功率譜密度Fig.10ThePSDofembankmentvibrationwhenthetrainspeedis150km/h

圖11為車速150 km/h時，距離軌道12 m處和15 m處地面振動速度功率譜密度。由圖可知，與天然路基相比，CFG復合路基加固后地面3~11 Hz振動功率譜值下降。距軌道12 m處地面振動譜值下降幅度大于距軌道15 m處，CFG復合路基對距離軌道較近地面振動的減小更明顯。

CFG復合路基中墊層-樁結構體系對路基振動的作用與波阻板(WIB)的作用類似。WIB板的隔振原理為“人工基巖”存在截止頻率，地面振源低于截止頻率無振動波，高于截止頻率則有隔振作用[25]。CFG樁及復合路基墊層結構類似于人工基巖，對低于截止頻率的振動有顯著減振作用，如圖11中CFG復合路基對3~11 Hz振動有明顯減小。

圖12為列車運行速度300 km/h時，距離軌道2 m處和4 m處路堤面振動速度功率譜密度。由圖可知，CFG復合路基加固后，距離軌道4 m處小于50 Hz和大于175 Hz振動譜值下降。車速為150 km/h時路堤邊緣(4 m處)振動譜值影響范圍為小于25 Hz和高于75 Hz的振動(參圖10)。車速提高至300 km/h后CFG復合路基對較低頻段的減振增加，對較高頻段的減振減小。CFG樁的波導作用導致復合路基顯著降低高頻振動，車速增大CFG復合路基對較高頻率振動的減振下降，CFG樁的波導作用減弱。

圖13為車速300 km/h時，距離軌道12 m和15 m處地面振動速度功率譜密度。由圖可知，與天然路基相比，采用CFG復合路基3~60 Hz地面振動功率譜值下降。距軌道12 m處地面振動譜值下降幅度大于15 m處，CFG復合路基對距離軌道較近地面振動的影響較大。車速為150 km/h時CFG復合路基的影響頻段為3~11 Hz(如圖11)，小于車速300 km/h時的影響頻段(3~60 Hz)，故車速提高后，CFG樁加固對地面振動的影響頻段范圍增大。

圖11 列車速度150km/h地面振動功率譜密度Fig.11ThePSDofgroundvibrationfarfromthetrackwhenthetrainspeedis150km/h圖12 列車速度300km/h路堤面振動功率譜密度Fig.12ThePSDofembankmentvibrationwhenthetrainspeedis300km/h圖13 列車速度300km/h遠離軌道地面振動功率譜密度Fig.13ThePSDofgroundvibrationfarfromthetrackwhenthetrainspeedis300km/h

圖14為車速分別為150 km/h、200 km/h、250 km/h和300 km/h時，路堤面和地面振動速度衰減。由圖可知，車速為300 km/h時，距軌道3 m處天然路基和復合路基路堤面振動速度分別為12 mm/s和6.1 mm/s，相差5.9 mm/s；路堤邊緣處振動速度分別為8.9 mm/s和4.0 mm/s，相差4.9 mm/s。CFG復合路基路堤面振動速度較天然路基路堤面有顯著下降，且復合路基路堤邊緣的振動速度減小較大。由圖還知，車速越快，CFG復合路基對路堤振動的影響越大，路堤邊緣的振動速度減小越多。

CFG復合路基對地面低頻振動的隔振作用與WIB波阻板相似，其隔振效果可以用振動衰減系數AR描述[26]：

(20)

圖15為CFG復合路基地面振動衰減系數變化。由圖可知，復合路基路堤面振動幅值的衰減系數為055~0.70，路堤邊緣衰減系數最小，振動幅值衰減最大；距離軌道15 m處的振幅衰減系數為0.90~ 0.95，振動幅值衰減小。由圖還知，車速越大，路堤面的振動衰減系數越小，復合路基對路堤面的減振效果越明顯。

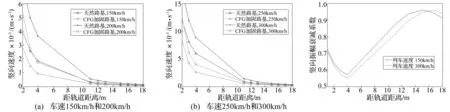
圖14 不同列車速度振動速度衰減圖Fig.14Thegroundvibrationattenuationfordifferenttrainspeeds圖15 地面豎向振幅衰減系數圖Fig.15Theamplitudeattenuationcoefficientfortheverticalvibration

5結論

(1) 采用美國功率譜描述鋼軌不平順，采用非線性接觸Hertzian公式描述輪軌接觸，建立了CFG樁復合鐵路路基動力有限元模型，采用振型分解法和2.5維有限元分析CFG樁復合路基對列車運行引起堤面和地面振動的影響。對比地面振動實測結果和數值結果，表明2.5維有限元模型可有效模擬CFG復合路基的地面振動。

(2) CFG樁復合路基路堤面振動速度較天然路基小，復合路基路堤面的振動衰減快，路堤邊緣的振動速度減小。CFG復合路基路堤邊緣的高頻振動減小顯著，增大了路堤的動力穩定性。

(3) CFG樁復合路基墊層和樁體對路基振動的影響頻段有差異。CFG樁對高頻振動有波導作用，減小了復合路基外的高頻振動；CFG樁復合路基及墊層對中低振動的影響與波阻板類似，減小了路堤外中低頻的地面振動。

(4) 車速影響CFG樁復合路基的隔振效果。車速較高時，CFG樁對高頻振動的波導作用減小，復合路基對高頻振動削減降低；同時路基墊層結構對振動的影響頻段范圍增大。車速越大CFG樁復合路基對路堤面減振效果越明顯，故CFG樁復合路基降低了列車運行引起的地面振動。

參 考 文 獻

[1] Xia H, Zhang N, Cao Y M. Experimental study of train-induced vibrations of environments and buildings[J]. Journal of Sound and Vibration, 2005, 280(3):1017-1029.

[2] Eason G. The stresses produced in a semi-infinite solid by a moving surface force[J]. International Journal of Engineering Sciences, 1962, 2: 581-609.

[3] Metrikine A V, Dieterman H A. Lateral vibrations of an axially compressed beam on an elastic half-space due to a moving lateral load[J]. European Journal of Mechanics-A/Solids, 1999, 18(1): 147-158.

[4] Dinkel J, Grundmann H. Winkler parameters for railway dynamics derived from 3-D half space analysis[C]//Fourth European Conference on Structural Dynamics: EURODYN’99, 1999: 831-836.

[5] Yang Y B, Hung H H. A 2.5 D finite/infinite element approach for modelling visco-elastic bodies subjected to moving loads[J]. International Journal for Numerical Methods in Engineering, 2001, 51(11): 1317-1336.

[6] 邊學成，陳云敏. 基于 2.5 維有限元方法分析列車荷載產生的地基波動[J]. 巖石力學與工程學報，2006，25(11): 2335-2342.

BIAN Xue-cheng, CHEN Yun-ming. Ground vibration generated by train moving loadings using 2.5D finite element method[J].Chinese Journal of Rock Mechanics and Engineering,2006, 25(11): 2335-2342.

[7] Gao G Y, Chen Q S, He J F, et al. Investigation of ground vibration due to trains moving on saturated multi-layered ground by 2.5 D finite element method[J]. Soil Dynamics and Earthquake Engineering, 2012, 40: 87-98.

[8] Kouroussis G, Conti C, Verlinden O. Investigating the influence of soil properties on railway traffic vibration using a numerical model[J]. Vehicle System Dynamics, 2013, 51(3): 421-442.

[9] 李佳，高廣運，趙宏. 基于 2.5 維有限元法分析橫觀各向同性地基上列車運行引起的地面振動[J]. 巖石力學與工程學報，2013，32(1): 78-87.

LI Jia, GAO Guang-yun, ZHAO Hong. Study of ground vibration induced by train load in transversely isotropic soil using 2.5D finite element method[J].Chinese Journal of Rock Mechanics and Engineering,2013, 32(1): 78-87.

[10] 龔曉南. 復合地基理論及工程應用[M]. 北京: 中國建筑工業出版社，2002年11月.

[11] Thach P N, Liu H L, Kong G Q. Evaluation of PCC pile method in mitigating embankment vibrations from high-speed train[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(12): 2225-2228.

[12] Thach P N, Liu H L, Kong G Q. Vibration analysis of pile-supported embankments under high-speed train passage[J]. Soil Dynamics and Earthquake Engineering, 2013, 55: 92-99.

[13] 王維玉，趙拓，丁繼輝. CFG樁復合地基動力特性和時程響應影響因素分析[J]. 巖土工程學報，2010，2: 115-118.

WANG Wei-yu, ZHAO Tuo, DING Ji-hui.Influencing factors of dynamic characteristics and response of cement-fly ash-gravel pile composite foundation[J]. Chinese Journal of Geotechnical Engineering,2010,2:115-118.

[14] 屈暢姿，王永和，魏麗敏，等. 武廣高速鐵路路基振動現場測試與分析[J]. 巖土力學，2012, 33(5): 1451-61.

QU Chang-zi, WANG Yong-he, WEI Li-min, et al. In-situ test and analysis of vibration of subgrade for Wuhan-Guangzhou high-speed railway[J]. Rock and Soil Mechanics, 2012, 33(5): 1451-1461.

[15] 劉麗萍，黃義，李向陽. 板-復合地基動力分析半解析元法[J]. 巖土力學，2007，28(4): 753-757.

LIU Li-ping, HUANG Yi, LI Xiang-yang. A semi-analytical method for dynamical analysis of slab and composite foundation[J].Rock and Soil Mechanics, 2007, 28(4): 753-757.

[16] 康文生. 高速鐵路低矮路堤灰土樁復合地基的動力特性分析[J]. 路基工程，2012，(3): 36-38.

KANG Wen-sheng. Analysis on dynamic characteristics of lime-soil pile composite foundation of low embankment along high-speed railway[J]. Subgrade Engineering,2012, (3): 36-38.

[17] 韓海燕. 軟土路基上高速列車引起地面振動的數值模擬分析[D]. 成都:西南交通大學, 2012.

[18] Kouroussis G, Verlinden O, Conti C. Free field vibrations caused by high-speed lines: Measurement and time domain simulation[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(4): 692-707.

[19] 李廣慧.車輛-無碴軌道-橋梁系統振動特性及其應用[M]. 鄭州: 黃河水利出版社，2007.

[20] Kouroussis G, Verlinden O, Conti C, Finite-dynamic model for infinite media: corrected solution of viscous boundary efficiency[J]. Eng. Mech. ASCE, 2011, 137(7) 509-511.

[21] 羅震. 高速鐵路無砟軌道結構受力及輪軌動力作用分析[D]. 成都:西南交通大學，2008.

[22] Connolly D, Giannopoulos A, Forde M C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments[J]. Soil Dynamics and Earthquake Engineering, 2013, 46: 13-19.

[23] 王漾，周萌，宮全美，等. 高速鐵路CFG樁網復合結構設計參數分析[J]. 華東交通大學學報，2011，27(6): 17-22.

WANG Yang, ZHOU Meng, GONG Quan-mei, et al.An analysis on design parameters of CFG pile-net composite structure of high-speed railway[J]. Journal of East China Jiaotong University, 2011, 27(6): 17-22.

[24] Krylov V V. Effects of the embankment topography and track curvature on ground vibration boom from high-speed trains[J]. Proceedings of theSymposium EURODYN, 2002: 473-478.

[25] Takemiya H. Vibration propagation and mitigation for a pile-supported foundation by honeycomb-shaped WIB[J]. Proceedings of Environment Vibration: Prediction,Monitoring and Evaluation, Hangzhou, 2003: 267-290.

[26] 高廣運，陳功奇，張博. 列車荷載下豎向非均勻地基波阻板主動隔振分析[J]. 振動與沖擊，2013，32(22): 57-62.

第一作者 高廣運 男，博士，教授，博士生導師，1961年生

摘要：結合上部列車-軌道模型與下部有限元路基模型，建立了列車-軌道-路基整體動力分析模型，分析了CFG復合路基對地面振動的影響。列車采用多質點彈簧-阻尼器模擬，鋼軌采用歐拉梁模擬并考慮了鋼軌隨機不平順影響，列車-軌道體系采用振型分解法求解；鐵路路基經有限元離散后采用2.5維有限元方法求解，采用粘滯阻尼吸波邊界減小邊界反射，CFG樁采用等代模量樁墻模擬。分析了CFG樁復合路基對地面振動衰減和振動頻譜的影響。結果表明：CFG樁復合路基對地面振動的影響分為CFG樁體的影響和墊層影響；CFG樁體對路基中的高頻振動有波導作用，可減小遠離路堤的高頻振動；復合路基墊層可降低中低頻振動。CFG復合路基減小了路堤邊緣的高頻振動，提高了路堤邊坡的動力穩定性。

關鍵詞：地面振動；CFG樁復合路基；頻譜分析；2.5維有限元；波導作用

Dynamic response of CFG pile composite subgrade induced by moving train loadings

GAOGuan-yun1,2,LIShao-yi1,2(1. Department of Geotechnical Engineering，Tongji University，Shanghai 200092，China；2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China)

Abstract:A numerical train-track-subgrade model was established including an upper train-track model and an under subgrade FE model to analyze the influence of CFG pile composite subgrade on the ground vibration. The train was simulated by using a multiple mass-spring-damper model. The track was modeled as a Euler beam with consideration of random rail irregularities. The train-track model was solved by the modal decomposition method. The railway subgrade was discretized and solved by 2.5D FEM with a viscous damping absorbing boundary to reduce the reflection wave. The CFG pile was modeled as a pile wall with modified elastic modulus. The influences of the CFG pile composite subgrade on ground vibration attenuation and vibration frequency spectrum were discussed. The results show that the influences of the CFG pile composite subgrade on ground vibration are comprised of the influence of CFG pile and the influence of cushion. The CFG pile has the waveguide effect on high frequency vibration and reduces the high frequency vibration originated from the embankment; the cushion of the composite subgrade affects the ground vibration by reducing low and medium frequency vibration. Besides, the composite subgrade reduces the high frequency vibration at the edge of embankment, that improves the dynamic stability of the slope of embankment.

Key words:ground vibration; CFG pile composite subgrade; spectral analysis; 2.5D FEM; waveguide effect

中圖分類號:TU435

文獻標志碼：A DOI:10.13465/j.cnki.jvs.2015.24.023

收稿日期：2014-10-10修改稿收到日期：2014-12-25

基金項目：國家自然科學基金資助項目(51178342)