一種改進(jìn)的特征系統(tǒng)實(shí)現(xiàn)算法及其在海洋平臺上的應(yīng)用
辛峻峰, 張永波, 盛進(jìn)路
(1.青島科技大學(xué) 機(jī)電學(xué)院,山東 青島 266061;2.青島國家海洋科學(xué)研究中心,山東 青島 266071;3.重慶交通大學(xué) 交通運(yùn)輸學(xué)院,重慶 400074;4.大連海事大學(xué) 船機(jī)修造工程交通行業(yè)重點(diǎn)實(shí)驗(yàn)室,大連 116026)
?
一種改進(jìn)的特征系統(tǒng)實(shí)現(xiàn)算法及其在海洋平臺上的應(yīng)用
辛峻峰1, 張永波2, 盛進(jìn)路3,4
(1.青島科技大學(xué) 機(jī)電學(xué)院,山東 青島266061;2.青島國家海洋科學(xué)研究中心,山東 青島266071;3.重慶交通大學(xué) 交通運(yùn)輸學(xué)院,重慶400074;4.大連海事大學(xué) 船機(jī)修造工程交通行業(yè)重點(diǎn)實(shí)驗(yàn)室,大連116026)
有效的模態(tài)識別方法能精確地得到結(jié)構(gòu)的相關(guān)參數(shù),從而可以準(zhǔn)確地掌握大型結(jié)構(gòu)的健康狀況。國內(nèi)外許多學(xué)者提出了基于時域響應(yīng)的模態(tài)參數(shù)識別方法,如復(fù)指數(shù)法(Complex Exponential Method, CEM)、時間序列法(Time Series Method,TSM)、隨機(jī)減量法(Random Decrement Technique, RDT)、隨機(jī)子空間法(Stochastic Subspace Identification Method, SSI)等。其中,ERA是目前為止沖擊和張拉激勵下較為先進(jìn)高效的模態(tài)參數(shù)識別方法之一。它能夠更精確地提取海洋平臺等大型結(jié)構(gòu)的模態(tài)參數(shù)[1-3]。
ERA是一種多輸入多輸出的時域模態(tài)參數(shù)識別技術(shù)。1984年Juang[1]首先將其應(yīng)用到結(jié)動力學(xué)領(lǐng)域,目前在國外航天領(lǐng)域廣泛使用。但是當(dāng)數(shù)據(jù)的信噪比較低時,ERA方法的運(yùn)用受到限制。針對于此,本文首先基于矩陣映射理論提出了改進(jìn)的ERA算法-C/ERA,繼而通過五自由度阻尼彈簧質(zhì)量系統(tǒng)仿真和導(dǎo)管架平臺縮尺模型的物理模型試驗(yàn)將ERA和C/ERA兩種方法進(jìn)行了對比。
1C/ERA基本理論
結(jié)構(gòu)的狀態(tài)可用下面的微分方程表示(m表示輸入數(shù)量、n表示輸出數(shù)量)[1,4]:
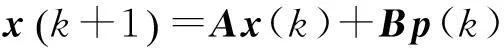
y(k)=Cx(k)
(1)
式中:x(k)x(k)為kΔt時刻系統(tǒng)的狀態(tài)矢量(2n維); y(k)為kΔt時刻系統(tǒng)的響應(yīng)矢量(n維);p(k)為kΔt時刻系統(tǒng)的激勵矢量(m維)。A是系統(tǒng)矩陣, B是控制矩陣,C是輸出矩陣;其中Δt為采樣時間間隔。
基于脈沖響應(yīng)函數(shù)矩陣序列(Markov參數(shù))構(gòu)建廣義Hankel矩陣
H(k-1)=
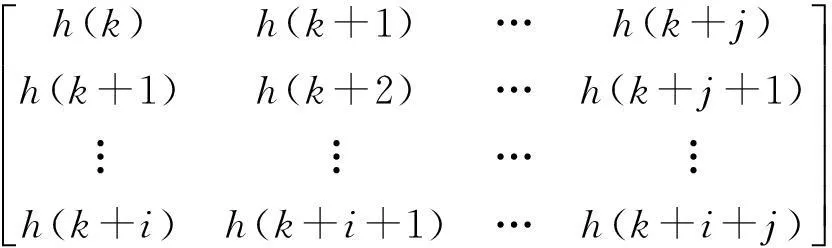
(2)
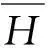
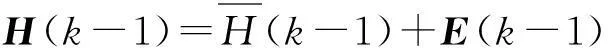
(3)
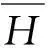

A=S-1/2UTH(1)VS-1/2
B=S-1/2VTE
C=ETmUS1/2
(4)
2數(shù)值仿真
基于Matlab建立了一個五自由度質(zhì)量-彈簧-阻尼系統(tǒng)數(shù)值模型[7],如圖1所示。

圖1 自由度彈簧-質(zhì)量-阻尼系統(tǒng)Fig.1 A 5-DOF mass-spring-dashpot system
每個單元的質(zhì)量、剛度和阻尼系數(shù)分別取為:mn= 50 kg,kn= 2.9 × 107N/m,cn= 1 000 N·s/m。位移記為xn,其中n=1,…,5。通過特征值分析,得到5階模態(tài)頻率的理論值為:34.499、100.700、158.730、203.880、232.520 Hz;5階模態(tài)阻尼比的理論值為:0.003 737、0.010 909、0.017 197、0.022 092、0.025 198[3]。
沖擊荷載是用Matlab impulse函數(shù)生成的單位脈沖(見圖2),繼而將其加載到靠固定端的質(zhì)量塊上 (見圖1)。
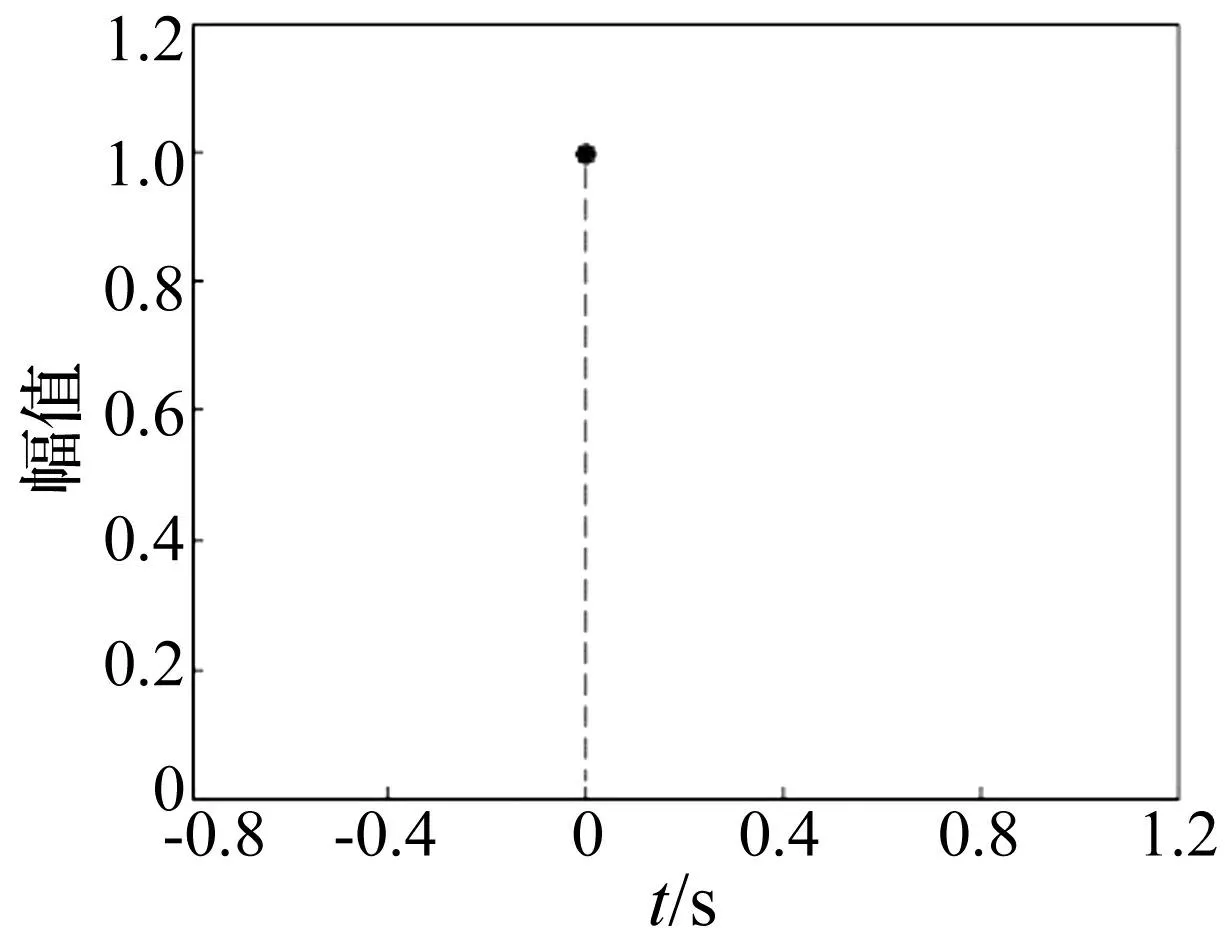
圖2 單位脈沖Fig.2 Unit impulse
本文采用靠固定端質(zhì)量塊輸出的脈沖響應(yīng)作為待用數(shù)據(jù),并加入20%方差為1.0103的隨機(jī)噪聲(見圖3)。
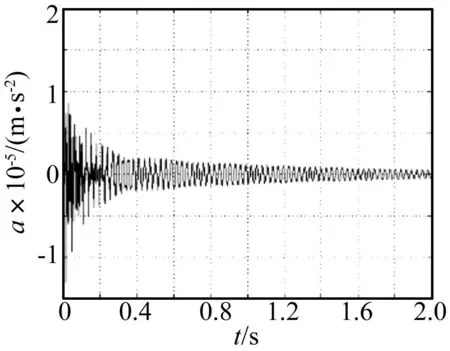
圖3 靠固定端質(zhì)量塊的響應(yīng)Fig.3 Response signal of the first mass
在方法的使用方式上,本文將ERA和C/ERA的Hankel矩陣維數(shù)都設(shè)定為i=512。
在展示工具的選擇上,本文采用了穩(wěn)定圖,其中采用了信號的傅里葉變換作為背景,顯示模態(tài)階數(shù)在0到20或25之間模態(tài)識別結(jié)果的情況。對于同一模態(tài),如果前后兩次識別結(jié)果同一模態(tài)的模態(tài)頻率誤差在1%,同時響應(yīng)阻尼的識別結(jié)果的誤差在5%,即
則此次識別的結(jié)果標(biāo)識為穩(wěn)定,否則為不穩(wěn)定。
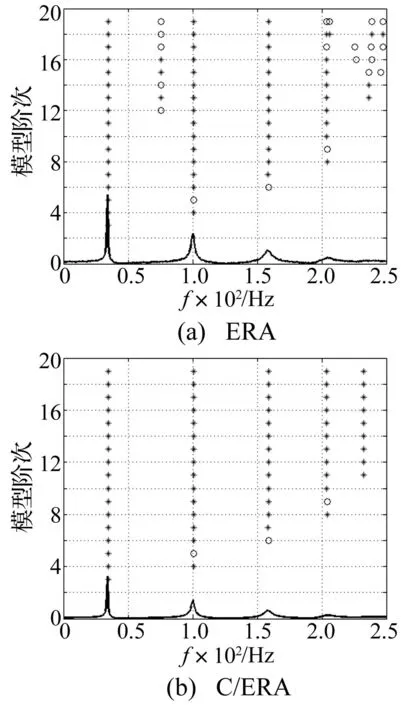
圖4 ERA(a)和 C/ERA (b)沖擊激勵下穩(wěn)定圖(*穩(wěn)定,o不穩(wěn)定)Fig.4 Stability Diagram for ERA (a) and C/ERA(b) under impulse loading(*stable,o unstable)
從圖4中能夠很容易發(fā)現(xiàn),C/ERA(圖4b)的識別結(jié)果明顯優(yōu)于ERA(圖4a)的識別結(jié)果:
(1) C/ERA(圖4b)的穩(wěn)定圖非常干凈,而ERA(圖4a)的識別結(jié)果非常雜亂(橫軸50~100 Hz之間出現(xiàn)了虛假模態(tài),橫軸200 Hz之后縱軸12~20的區(qū)域內(nèi)非常混亂),這說明C/ERA比ERA有更強(qiáng)的消噪能力。
(2) ERA(圖4a)只能識別出前三階模態(tài)(橫軸在34.499 Hz、100.700 Hz、158.730 Hz處對應(yīng)定的紅色直線,203.880 Hz處對應(yīng)的直線在縱軸17開始發(fā)生混亂,232.520 Hz處沒有對應(yīng)的穩(wěn)定的直線),而C/ERA(圖b)清晰地識別出了0~250 Hz之間的5個模態(tài)(橫軸在34.499 Hz、100.700 Hz、158.730 Hz、203.880 Hz、232.520 Hz處對應(yīng)穩(wěn)定的紅色直線)。這說明C/ERA能夠比ERA識別出更多的模態(tài),尤其對高階模態(tài)有更強(qiáng)的識別能力。
穩(wěn)定圖的對比結(jié)果清晰地展示了:較ERA而言,C/ERA消噪能力更強(qiáng)從而能夠識別出更多的高階模態(tài)。
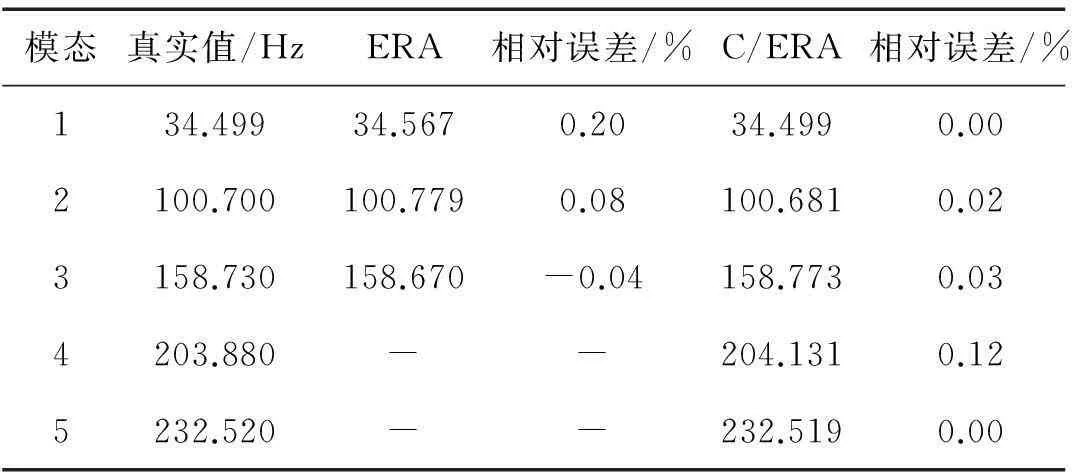
表1 頻率估計(jì)值(定階為10)
表1和2分別羅列了兩種方法模態(tài)頻率和模態(tài)阻尼的估計(jì)結(jié)果,可以看到C/ERA不但能識別出第4和第5階高階模態(tài)(203.880和232.520 Hz),而且在低階模態(tài)阻尼的估計(jì)上有較大改善(相對誤差超過5%):第一階模態(tài)阻尼相對誤差由-42.52%降到-2.19%,第二階模態(tài)阻尼由7.48%降到-1.6%。
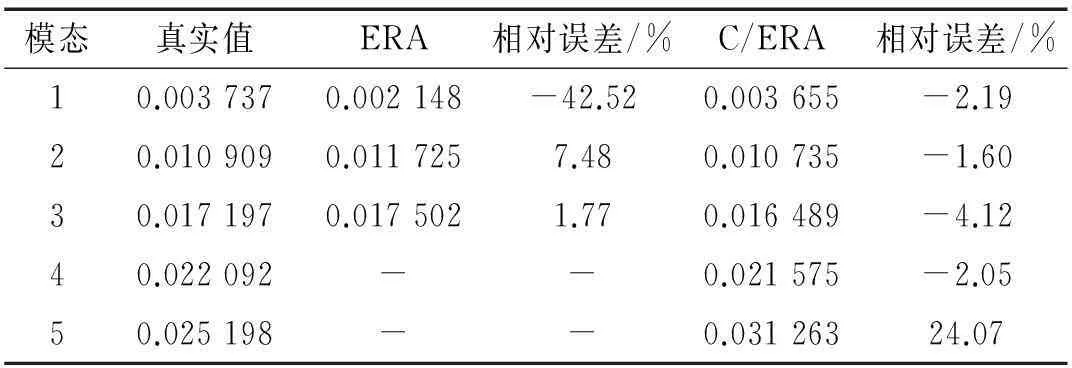
表2 阻尼估計(jì)值的均值(定階為10)
總之,五自由度質(zhì)量-彈簧-阻尼系統(tǒng)沖擊激勵仿真證明:較/ERA 而言,C/ERA消噪能力更強(qiáng),從而導(dǎo)致該算法對高階模態(tài)有更強(qiáng)的識別能力,并且對低階模態(tài)的阻尼有更精確的識別結(jié)果。
3導(dǎo)管架平臺試驗(yàn)
3.1目標(biāo)平臺

圖5 目標(biāo)平臺Fig.5 Target platform
某井組平臺位于東經(jīng)118°50′57″、北緯38°14′10″,是一座6井式采油、修井一體化平臺,工藝平臺為四腿式樁基鋼制導(dǎo)管架結(jié)構(gòu)。井口平臺與計(jì)量平臺之間以鋼制衍架結(jié)構(gòu)棧橋連接。海洋平臺如圖5所示。
3.2物理模型

圖6 海洋平臺物理模型Fig.6 Physical model of jacket platform
導(dǎo)管架物理模型采用鋼管制作,在Y向設(shè)3根主梁,X向設(shè)2根,有3層水平橫撐,分別位于-88 cm、142 cm和188 cm處設(shè)水平橫撐,在88 cm至-142 cm處設(shè)豎向斜撐,主要構(gòu)件的尺寸為:主腿25×2.5 mm,水平撐桿16×1.5 mm,斜撐桿16×1.5 mm。模型的構(gòu)件尺寸見表3,平臺物理模型見圖6~圖7所示,對應(yīng)數(shù)值模型的模態(tài)信息見表4所示。

圖7 海洋平臺物理模型實(shí)際比例Fig.7 Actual proportion of physical model of jacket platform

主要構(gòu)件原型尺寸/mm模型尺寸/mm主腿1350×2425×2.5水平撐桿700×2216×1.5斜撐桿500×1816×1.5
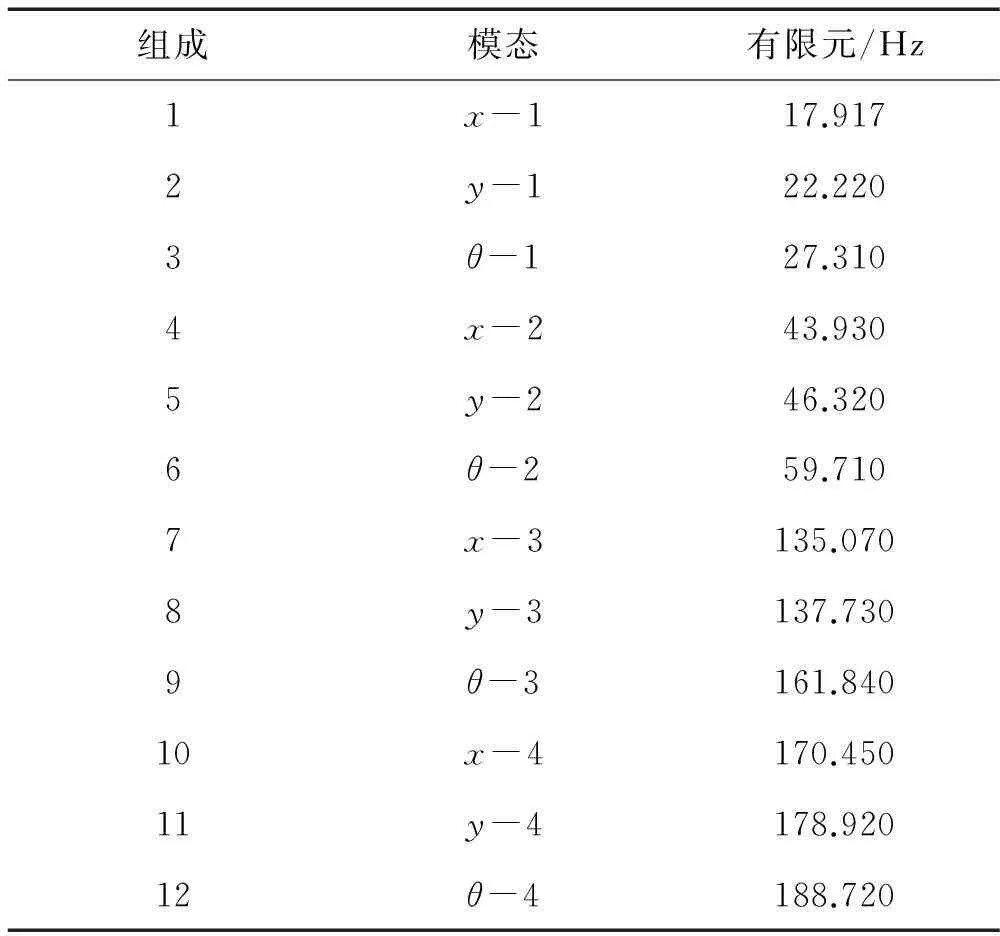
表4 有限元結(jié)果
3.3沖擊激勵加載
用橡皮錘在選定目標(biāo)平臺甲板上左側(cè)節(jié)點(diǎn)(見圖8),在第0 s施加6 kN的沖擊力,記錄平臺各個節(jié)點(diǎn)的自由振動加速度響應(yīng)。
3.4響應(yīng)數(shù)據(jù)獲取
以500 Hz采樣頻率用傳感器A采集了1 024個數(shù)據(jù)點(diǎn),約2 s(見圖9)。同樣將ERA和C/ERA的Hankel矩陣維數(shù)都設(shè)定為i=512。
從穩(wěn)定圖的分析結(jié)果中(圖10)能夠發(fā)現(xiàn):
(1) C/ERA(圖b)的穩(wěn)定圖更清晰,而ERA(圖a)的識別結(jié)果在橫軸130Hz之后縱軸10-25的區(qū)域內(nèi)非常雜亂,這說明C/ERA比ERA有更強(qiáng)的消噪能力。
(2) ERA(圖a)和C/ERA(圖b)都能識別出前五階模態(tài)(橫軸大約在22 Hz、27 Hz、46 Hz、59 Hz、137 Hz處對應(yīng)穩(wěn)定的紅色直線),但是在高階模態(tài)的識別上(橫軸150 Hz之后),C/ERA能非常穩(wěn)定地識別出三個模態(tài)(橫軸大約在160 Hz、180 Hz、190 Hz處),而ERA在同樣的區(qū)域相對混亂,這證明C/ERA對高階模態(tài)有更強(qiáng)的識別能力。

圖9 靠固定端質(zhì)量塊響應(yīng)Fig.9Responseofmassclosetofixedpoint圖10 物理模型試驗(yàn)ERA(a)和C/ERA(b)沖擊激勵下穩(wěn)定圖(*穩(wěn)定,o不穩(wěn)定)Fig.10StabilityDiagramforERA(a)andC/ERA(b)fromphysicalmodelofjacketplatformunderimpulseloading(*stable,ounstable)
穩(wěn)定圖的對比結(jié)果清晰地展示了:較ERA而言,C/ERA消噪能力能強(qiáng),由此該方法能夠識別出更多的模態(tài),尤其對高階模態(tài)有更強(qiáng)的識別能力。
在模態(tài)頻率(表5)的估計(jì)上,跟前6階模態(tài)的識別精度相比較,C/ERA對高階模態(tài) (y-4和θ-4兩個模態(tài))的識別誤差(-7.02%和3.91%)并沒有出現(xiàn)較大變化,保持了相對穩(wěn)定,由此可見該方法有能力穩(wěn)定地估計(jì)高階模態(tài)頻率。
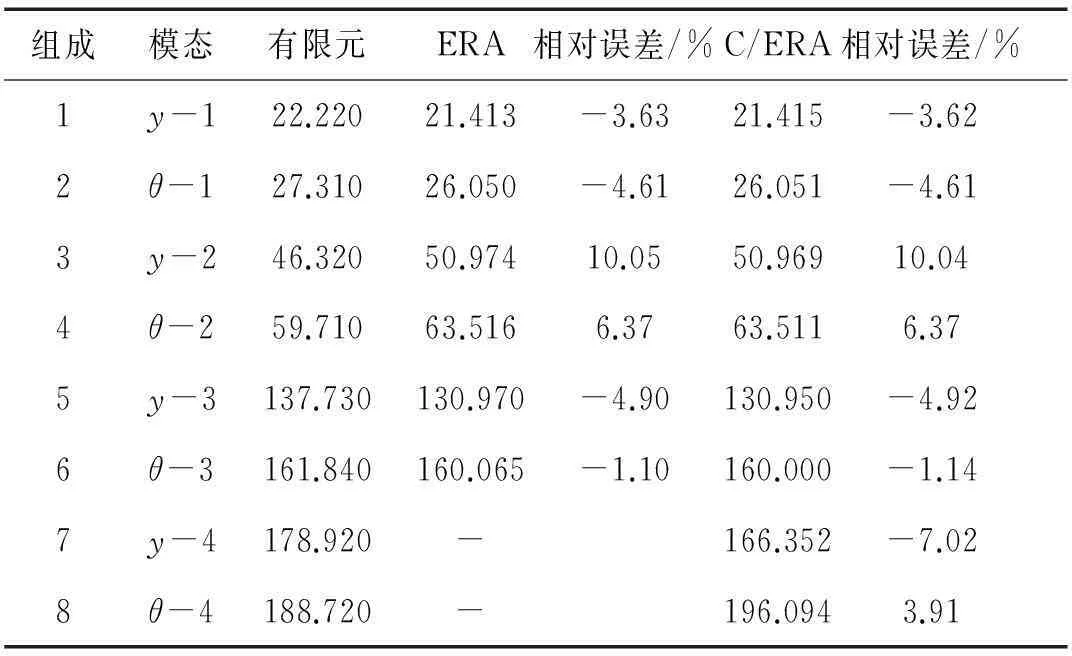
表5 頻率估計(jì)值(定階為20).
總之,導(dǎo)管架平臺物理模型試驗(yàn)沖擊激勵試驗(yàn)與數(shù)值仿真的研究結(jié)論基本一致:C/ERA消噪能力更強(qiáng)從而導(dǎo)致該方法對高階模態(tài)更加敏感,能夠識別出更多的高階模態(tài)。
4結(jié)論
本文提出了傳統(tǒng)ERA的改進(jìn)方法-C/ERA,該算法在ERA的奇異值截?cái)嗪螅亟℉ankel矩陣,繼而將矩陣中各元素由其所在的反對角線上的元素?cái)?shù)學(xué)平均值代替并引入Frobenius范數(shù)準(zhǔn)則控制迭代次數(shù)。最終通過五自由度阻尼彈簧質(zhì)量系統(tǒng)仿真和導(dǎo)管架平臺縮尺模型的物理模型錘擊試驗(yàn)驗(yàn)證了該方法的優(yōu)勢:①更強(qiáng)的消噪能力;②對高階模態(tài)更敏感;③對低階模態(tài)阻尼有更精確的識別能力。由此,本文提出的C/ERA方法比ERA更適合作為今后海洋平臺等大型結(jié)構(gòu)沖擊激勵下的模態(tài)參數(shù)識別工具。
參 考 文 獻(xiàn)
[1] Juang J N,Pappa R S. An eigensystem realizationm algorithm (ERA) for modal parameter identification and model reduction[J]. Journal of Guidance, Control, and Dynamics. 1985, 8(5): 620-627.
[2] Hu S L J, Li P, Vincent H, et al. Modal parameter estimation for jacket-type platforms using free-vibration data[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2011:1943-1460.
[3] 辛峻峰,盛進(jìn)路,張永波.數(shù)據(jù)驅(qū)動隨機(jī)子空間法矩陣維數(shù)選擇與噪聲問題研究[J]. 振動與沖擊,2013,32(16):152-157.
XIN Jun-feng,SHENG Jin-lu,ZHANG Yong-bo.Relation between noise and matrix dimension of data-driven stochostic subspace identification method[J]. Journal of Vibration and Shock, 2013,32(16):152-157.
[4] Cunha A, Caetano E. Experimental modal analysis of civil engineering structures[J]. Sound and Vibration,2006:12-20.
[5] Juang J N,Pappa R S. Effects of noise on modal parameters identified by the eigensystem realization algorithm[J]. Journal of Guidance, Control, and Dynamics,1986, 9(3):294-303.
[6] Cadzow J A. Signal enhancement-A composite property mapping algorithm[J]. IEEE Trans Acoust, Speech, Signal Proeess,1988,36(1):49-62.
[7] Chu M T, Funderlic R E, Plemmons R J. Structured low rank approximation[J].Linear Algebra Appl.June2003,366:157-172.
[8] ANSYS.Inc,ed.,2004. ANSYS Academic Research.Release 9.0. Help System. Coupled Field Analysis Guide10.
第一作者 辛峻峰 男,博士,講師,1982年12月生
摘要:基于矩陣映射理論,提出一種ERA的改進(jìn)算法--C/ERA。該算法在傳統(tǒng)的ERA方法奇異值截?cái)噙^程之后重建Hankel矩陣,繼而將矩陣各元素由其所在反對角線上的元素?cái)?shù)學(xué)平均值代替并引入Frobenius第二范數(shù)準(zhǔn)則控制迭代次數(shù)。五自由度阻尼彈簧質(zhì)量系統(tǒng)仿真以及海洋平臺縮尺模型物理模型的試驗(yàn)結(jié)果表明: C/ERA方法能更強(qiáng)的消噪能力,對高階模態(tài)更敏感而且在低階模態(tài)阻尼的識別上有更高的識別精度。
關(guān)鍵詞:模態(tài)參數(shù)識別; C/ERA;消噪
Improved eigen system realization algorithm and its application in the analysis of ocean platform
XINJun-feng1,ZHANGYong-bo2,SHENGJin-lu3,4(1. Qingdao University of Science and Technology, Qingdao 266061, China; 2. Qingdao National Oceanographic center, Qingdao 266071, China;3. Traffic and Transportation Colleage, Chongqing Jiaotong University, Chongqing 400074, China;4. Key Laboratory of Ship Mechanics Made Traffic Engineering Industry, Dalian Maritime University, Dalian 116026, China)
Abstract:Based on the matrix mapping theory, an improved eigensystem realization algorithm(ERA), called C/ERA, was proposed. In the algorithm, a Hankel matrix was rebuilt by replacing all the elements on each anti-subdiagonal by the arithmetic average of the elements on the anti-subdiagonal, and the concept of using the Frobenius norm (L2-norm) to control iterations number was introduced for enhancing the denoising ability of ERA. In accordance with the simulation results of a 5-DOF mass-spring-dashpot system and the experimental data of the model of a jacket-type platform under impact loading, it is proved that C/ERA has a better capacity of de-noising, higher accuracy for low order modes and can identify more high order modes than ERA does.
Key words:modal parameter identification; C/ERA; noising
中圖分類號:O32
文獻(xiàn)標(biāo)志碼:A DOI:10.13465/j.cnki.jvs.2015.24.033
通信作者盛進(jìn)路 男,博士,副教授,1978年生
收稿日期:2014-08-07修改稿收到日期:2015-03-31
基金項(xiàng)目:青島市建設(shè)科技計(jì)劃項(xiàng)目(JK2015-15);青島市青年專項(xiàng)(14-2-4-116-jch);大連海事大學(xué)船機(jī)修造工程交通行業(yè)重點(diǎn)實(shí)驗(yàn)室開放課題

