分數階電路階躍響應特性研究

王志蘭

（山西大學電力工程系，太原,030013）

分數階電路階躍響應特性研究

王志蘭

（山西大學電力工程系，太原,030013）

針對分數階動態電路，基于分數階微分方程的解析解，研究0~2階分數階動態電路的階躍響應。利用MATLAB軟件，得到不同階次分數階電路的階躍響應曲線，并與整數一階電路和二階電路的階躍響應作了對比研究，為今后分數階電路的研究奠定了基礎。

分數階電路；解析解；階躍響應

0 引言

分數階微積分是指階次為分數的微積分，當階次為整數時，等同于常規定義下的微積分運算。學者們認為，當前對電容和電感的整數階物理描述是理想模型，分數階的描述才是更真實的，本文將基于分數階來研究動態電路的響應。

求解分數階系統，解析算法有拉氏變換法和傅里葉變換法，數值算法有Zhang and Shimizu法，L-1法和池田法等。數值算法雖然編程簡單，但計算精度取決于時間步長，若時間步長太小，計算時間過長。本文采用解析算法，精度較高，且所選系統為兩項分數階系統，大大降低了解析算法公式的復雜度。

1 兩項分數階微分方程的解析解

初值為零的兩項分數階微分方程為：

根據Podlubny的理論[4]和文獻[5]和[6]對兩項分數階微分方程的研究，給出上式的解析解：

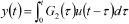
2 分數階動態電路

2.1 含一個分數階元件的動態電路

以RC串聯電路為例，研究分數階電抗的階躍響應。設分數階電容的階次為α∈(0,1)，以uc(t)為待求量，對應的微分方程為：

設電容初始儲能為零，即uc(0-)=0；為簡化方程，令R=1Ω，C=1F，當u(t)=時，利用MATLAB編程仿真，求得不同時電容電壓的單位階躍響應，如圖1。α=1時為整數階電路。

由仿真結果可以看出，隨著分數階電容階次的增大，穩定輸出增大，響應時間也增大。階次低于1時，響應曲線未出現振蕩，與一階系統的階躍響應曲線走向一致，但穩定輸出小于1。

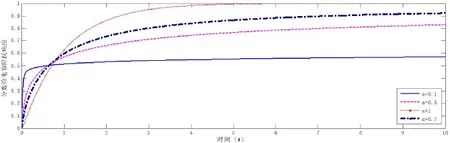
圖1 不同階次分數階動態電路的單位階躍響應

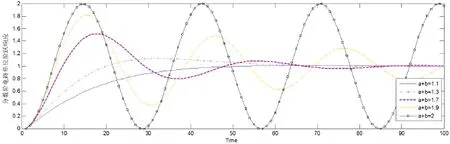
圖2 階次為1-2階電路的階躍響應

2.2 含兩個分數階元件的動態電路

用分數階電感和分數階電容元件并聯形成含兩個分數階元件的動態電路，電容和電感的階次分別為

α∈(0,1)和β∈(0,1)。以iL(t)為待求量，對應的方程為：

求解上式，得到不同階次的分數階電感和分數階電容組成的無阻尼電路的單位階躍響應，α+β＜1時同上分析，只分析α+β＞1的情況，結果如圖2。

可以看出，當階次大于1時，階躍響應開始出現振蕩，且隨著階次增大，振蕩加劇，直至2階系統的等幅振蕩階躍響應；同時，階次增大，達到穩態的時間變長，最大超調量變大。

3 結論

本文從拉氏變換的角度給出了分數階微分方程的解析解，分析了階次在0-2之間的分數階電路的單位階躍響應，與傳統整數階電路作了對比研究。研究表明分數階系統可取得比整數階系統更靈活的響應輸出和響應時間，可利用分數階元件實現對整數階系統的改進。

[1]周激流，蒲亦非，廖科．分數階微積分原理及其在現代信號分析與處理中的應用[M]．北京：科學出版社，2010．

[2]汪紀鋒.分數階系統控制性能分析[M]．北京：電子工業出版社，2010．

[3]王振濱，曹廣益．分數階動態系統的數值算法[J]．系統仿真學報，2004，16(3)：477-479，484．

[4]Podlubny I．Fractional Differential Equations[M]．San Diego：Academic Press，1999．

[5]王學彬．兩項分數階微分方程在控制系統的應用[J]．南平師專學報，2005，24(2)：16-19．

[6]Yizheng Hu，Yong Luo，Zhengyi Lu．Analytical solution of the linear fractional differential equation by Adomian decomposition method[J]．Computational and Applied Methematics，2008，215(1)：220-229．

Research on the Step Response Characteristics of Fractional Order Circuit

Wang Zhilan
(Department of Power Engineering,Shanxi University,Taiyuan,030013,China)

Based on the analytic solution of fractional differential equations,the paper investigates the step responses of fractional circuit with the order between zero and two.The simulation results are compared with the step responses of integer order circuit.This paper lays the foundation for the future research of the fractional order circuit.

fractional circuit;analytic solution;step response