LTE-A系統(tǒng)中改進(jìn)的信道估計(jì)算法的研究及實(shí)現(xiàn)

陳發(fā)堂 董 麗

(重慶郵電大學(xué)重慶市移動(dòng)通信技術(shù)重點(diǎn)實(shí)驗(yàn)室,重慶 400065)

?

LTE-A系統(tǒng)中改進(jìn)的信道估計(jì)算法的研究及實(shí)現(xiàn)

陳發(fā)堂 董 麗

(重慶郵電大學(xué)重慶市移動(dòng)通信技術(shù)重點(diǎn)實(shí)驗(yàn)室,重慶 400065)

先進(jìn)的長(zhǎng)期演進(jìn)(LTE-A) 系統(tǒng)接收端需要對(duì)多徑信道進(jìn)行動(dòng)態(tài)估計(jì)和跟蹤，以滿足相干解調(diào)的目的，準(zhǔn)確而有效的信道估計(jì)方法可以提高數(shù)據(jù)傳輸速率。針對(duì)線性最小均方誤差(LMMSE)信道估計(jì)矩陣求逆運(yùn)算復(fù)雜度大的問(wèn)題，提出一種基于Gauss-Seidel算法的低復(fù)雜度的LMMSE算法。通過(guò)對(duì)基于導(dǎo)頻的幾種常用的信道估計(jì)算法進(jìn)行對(duì)比分析和研究，得到的LMMSE 算法具有較低的誤比特率和算法復(fù)雜度。最后基于Gauss-Seidel算法,分別設(shè)計(jì)了低復(fù)雜度LMMSE算法的各個(gè)子模塊的DSP實(shí)現(xiàn)方案。

先進(jìn)的長(zhǎng)期演進(jìn)(LTE-A) 信道估計(jì) 相干解調(diào) 線性最小均方誤差(LMMSE)算法 Gauss-Seidel算法 最小二乘算法 DSP

0 引言

LTE-A系統(tǒng)以正交頻分復(fù)用(orthogonal frequency division multiplexing, OFDM)和多輸入多輸出(mutiple input multiple output, MIMO)等作為物理層的關(guān)鍵技術(shù)，具有更高的頻譜效率、更大的系統(tǒng)容量和對(duì)高速場(chǎng)景的支持等特點(diǎn)[1]。針對(duì)ITU的目標(biāo)，LTE-A的目標(biāo)峰值速率是下行1 Gbit/s，上行500 Mbit/s。更高的峰值速率要求接收端能夠高效準(zhǔn)確地將獲得的信道狀態(tài)信息反饋給發(fā)送端。信道估計(jì)算法作為物理層接收端的算法，為信號(hào)檢測(cè)提供條件，對(duì)數(shù)據(jù)的正確恢復(fù)起著關(guān)鍵作用[2]。

從算法先驗(yàn)的角度，信道估計(jì)算法大體上可以分為兩類：盲信道估計(jì)和非盲信道估計(jì)[3]。評(píng)價(jià)信道估計(jì)算法的優(yōu)劣性在于其誤碼率/誤塊率和實(shí)現(xiàn)復(fù)雜度。盲信道估計(jì)算法不需要導(dǎo)頻信號(hào)，因此具有較高的頻譜利用率，但是其收斂速度慢、實(shí)現(xiàn)復(fù)雜度高。基于導(dǎo)頻信號(hào)的非盲信道估計(jì)算法常用的有最小平方(least square,LS)[4]、最均方誤差(minimum mean square error,MMSE)[5]、線性最小均方誤差(linear minimum mean square error,LMMSE)[6]，其中LS信道估計(jì)算法簡(jiǎn)單且易于實(shí)現(xiàn)，但算法性能較差；MMSE信道估計(jì)算法性能較好，但算法復(fù)雜度高；LMMSE信道估計(jì)算法雖然降低了MMSE算法的計(jì)算復(fù)雜度，但其實(shí)現(xiàn)復(fù)雜度仍較高。

本文針對(duì)LTE-A系統(tǒng)中的幾種信道估計(jì)算法進(jìn)行分析研究，提出了低復(fù)雜度的LMMSE算法，在保證性能的條件下極大地降低了LMMSE算法的實(shí)現(xiàn)復(fù)雜度。

1 信道估計(jì)算法

1.1 LS算法

LS估計(jì)算法，即最小二乘算法[4]，不考慮噪聲的影響，其表達(dá)式為：

(1)

LS算法僅用一次乘法就可實(shí)現(xiàn)，該算法簡(jiǎn)單、復(fù)雜度低，在傳播信道條件不夠好的條件下，也能保證一定的性能，因此是實(shí)際工程中復(fù)雜度與性能較為折中的一種選擇。然而LS算法沒(méi)有考慮噪聲和子載波干擾的影響，會(huì)產(chǎn)生很高的均方誤差，在信道環(huán)境不理想的情況下，大大降低信道估計(jì)的準(zhǔn)確度。

1.2 MMSE算法

(2)

RHH=E{HHΗ}=[R(m-n)]

(4)式中:m、n為導(dǎo)頻位置；τrms為歸一化時(shí)延；τmax為最大多徑時(shí)延;N為導(dǎo)頻數(shù)目。

MMSE算法比LS算法性能好，但其缺點(diǎn)是實(shí)現(xiàn)復(fù)雜度比較高，需要對(duì)一個(gè)N維矩陣多次復(fù)數(shù)相乘且求逆。當(dāng)信道環(huán)境發(fā)生變化時(shí)，需要更新RHH矩陣，且在每一個(gè)子幀內(nèi)需要重新計(jì)算(XXΗ)-1，其實(shí)現(xiàn)復(fù)雜度很高。

1.3 LMMSE算法

E{(XXΗ)-1}=E{|1/xk|2}I

(5)

I是單位矩陣，并且信噪比為:

(6)

因此，LMMSE算法的表達(dá)式：

(7)

1.4 低復(fù)雜度LMMSE算法

為了進(jìn)一步降低實(shí)現(xiàn)的復(fù)雜度，本文提出一種基于Gauss-Seidel迭代算法[8]的低復(fù)雜度的LMMSE算法。令A(yù)=D-L-U，其中，D是對(duì)角矩陣，L是下三角矩陣，U是上三角矩陣，方程組Ax=b的矩陣迭代公式為：

x(k+1)=(D-L)-1Ux(k)+(D-L)-1b

(8)

由式(7)可知:

(9)

由式(3)、式(4)可知，RHH是酉矩陣，且有：

(10)

故式(9)可化簡(jiǎn)為：

(11)

由于R(0)=1，且R(i)=R*(-i)，因此：

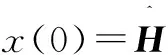
2 算法性能比較

2.1 誤比特率比較

利用Matlab對(duì)LTE-A系統(tǒng)中物理廣播信道(PBCH)的幾種基于導(dǎo)頻的信道估計(jì)算法進(jìn)行性能仿真分析。在PBCH鏈路中，仿真信道模型設(shè)置為擴(kuò)展的步行者信道模型(extendedpedestrianamodel，EPA)，噪聲為高斯白噪聲，系統(tǒng)帶寬為20MHz。在天線配置為4發(fā)4收的情況下，對(duì)QPSK調(diào)制方式下的LS、MMSE、LMMSE、低復(fù)雜度的LMMSE的誤比特率(biterrorrate,BER)進(jìn)行仿真分析比較，結(jié)果如圖1所示。

圖1 不同信道估計(jì)算法的性能比較

從圖1可以看出，LS算法的性能最差，MMSE算法比LMMSE算法的性能略好，低復(fù)雜度的LMMSE算法的性能略低于LMMSE算法和MMSE算法的性能。在QPSK調(diào)制方式下，基于導(dǎo)頻處的LS、MMSE、LMMSE和低復(fù)雜度的LMMSE信道估計(jì)算法的誤碼率隨著信噪比的增大而逐漸降低，LS算法由于放大了噪聲的影響，所以其性能是最差的；MMSE、LMMSE和低復(fù)雜度的LMMSE信道估計(jì)算法因?yàn)榭紤]了噪聲的影響，所以其性能優(yōu)于LS算法。

2.2 復(fù)雜度比較

假設(shè)一個(gè)OFDM符號(hào)上的導(dǎo)頻數(shù)目為N個(gè)，估計(jì)一個(gè)OFDM符號(hào)的計(jì)算復(fù)雜度如表1所示。

表1 算法復(fù)雜度

表1給出了4種算法的復(fù)雜度，可以看出LS算法的復(fù)雜度最低，MMSE算法的復(fù)雜度最高。LMMSE算法的復(fù)雜度低于MMSE算法的復(fù)雜度，而低復(fù)雜度的LMMSE算法由于將LMMSE算法中的常規(guī)矩陣求逆轉(zhuǎn)化為下三角矩陣求逆，所以其復(fù)雜度低于LMMSE算法。

3 DSP實(shí)現(xiàn)的設(shè)計(jì)流程

3.1 DSP簡(jiǎn)介

TMS320C6455是一款高性能的定點(diǎn)數(shù)字信號(hào)處理器[9-10]，其CPU采用哈佛結(jié)構(gòu)，該 DSP 核具有8個(gè)功能單元(包括2個(gè)乘法器和6個(gè)算術(shù)邏輯單元)，2組32位的寄存器和2條數(shù)據(jù)存取路徑；支持8/16/32/40/64位的數(shù)據(jù)訪問(wèn)能力和算術(shù)邏輯能力；超過(guò)32位的數(shù)據(jù)，像40位或者64位的數(shù)據(jù)，都使用寄存器對(duì)的形式。

3.2 DSP處理流程

基于PBCH接收端的信道估計(jì)處理流程，在常規(guī)循環(huán)前綴(CP)下，采用PBCH所占的6個(gè)資源塊(RB)，每個(gè)RB有12個(gè)子載波。從接收天線接收到的數(shù)據(jù)經(jīng)過(guò)解基帶信號(hào)模塊形成復(fù)數(shù)數(shù)據(jù)流，每個(gè)數(shù)據(jù)占用一個(gè)字的內(nèi)存，用32 bit表示。實(shí)部與虛部均采用Q15量化，各占16位，最高位為符號(hào)位。該實(shí)現(xiàn)方案包括3個(gè)模塊：導(dǎo)頻處基于LS算法的信道估計(jì)模塊、下三角矩陣求逆模塊和12階復(fù)數(shù)矩陣相乘模塊。3.2.1 LS算法的實(shí)現(xiàn)模塊

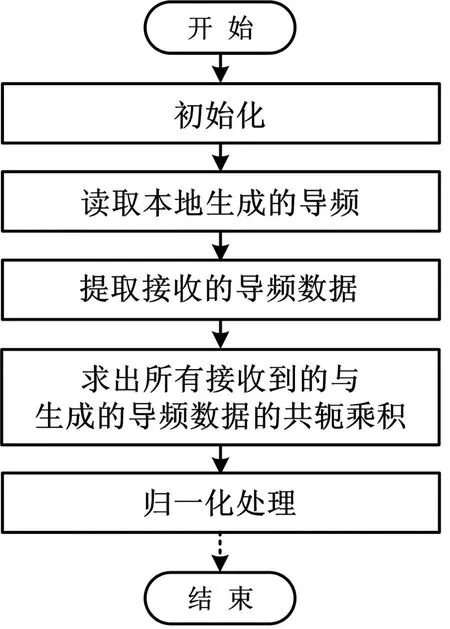
圖2 LS算法實(shí)現(xiàn)流程圖

從4根接收天線端口提取出參考信號(hào)以及本地生成的參考信號(hào)。對(duì)于每個(gè)天線端口，6個(gè)RB中共有12個(gè)小區(qū)參考信號(hào)。假定接收到的及本地生成的小區(qū)參考信號(hào)分別為A=a+bi，B=c+di，因參考信號(hào)為QPSK調(diào)制，故參考信號(hào)單位符號(hào)的能量為1。

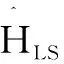
(ac+bd)+(bc-ad)i

(12)

為節(jié)省時(shí)間，采取并行指令的方法，4個(gè)天線端口同時(shí)進(jìn)行復(fù)數(shù)相乘，得到32 bit的實(shí)部和虛部，保留最大值并提取高16位存儲(chǔ)；完成12個(gè)參考信號(hào)的處理后，為降低精度損失，通過(guò)最大值進(jìn)行歸一化。

3.2.2 下三角矩陣求逆的實(shí)現(xiàn)模塊

從式(8)可知，需要計(jì)算D-L。

由上式可知D-L為下三角矩陣。此處需要對(duì)下三角矩陣求逆。

令Q=D-L，此時(shí)Q是12×12的下三角矩陣。

式中：i=1,2,...,n；j=1,2，...,i-1。

具體實(shí)現(xiàn)流程如圖3所示。

圖3 下三角矩陣求逆實(shí)現(xiàn)流程圖

3.2.3 矩陣相乘的實(shí)現(xiàn)模塊

根據(jù)式(8)可知，低復(fù)雜度的LMMSE算法的最后一步是實(shí)現(xiàn)12階矩陣的相乘。該方案采用每次兩個(gè)矩陣相乘、多次調(diào)用相乘模塊。設(shè)兩個(gè)相乘的矩陣分別為A、B，具體實(shí)現(xiàn)方法如圖4所示。

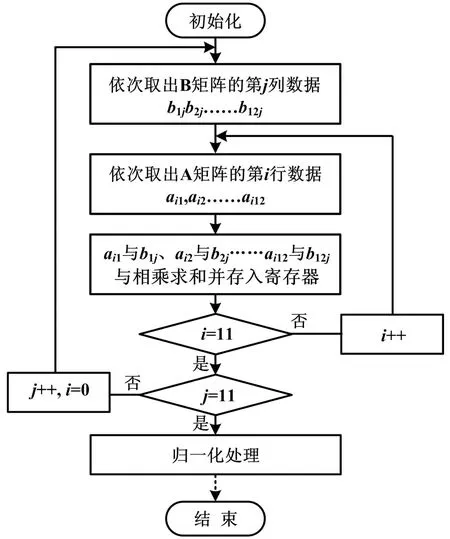
圖4 矩陣相乘實(shí)現(xiàn)流程圖

4 結(jié)束語(yǔ)

本文根據(jù)LTE-A系統(tǒng)的特點(diǎn)，提出一種低復(fù)雜度LMMSE算法，經(jīng)過(guò)鏈路級(jí)仿真對(duì)比研究，證明該算法較LS、MMSE和LMMSE算法具有高效性、可行性。本文詳細(xì)介紹了提出的低復(fù)雜度LMMSE算法的各個(gè)子模塊的DSP實(shí)現(xiàn)方案，并在TMS320C6455中得以實(shí)現(xiàn)。

[1] Abdullah M,Yonis A.Performance of LTE release 8 and release 10 in wireless communications[C]//Cyber Security,Cyber Warfare and Digital Forensic(CyberSec),2012 International Conference on,2012:236-241.

[2] 程光軍，王萍，張慶芳.LTE-A下行信道估計(jì)算法研究[J].電子測(cè)量技術(shù)，2013,36(10):34-37.

[3] 石磊，郭寶龍，李小平，等.一種低復(fù)雜度LMMSE信道估計(jì)算法[J].西安電子科技大學(xué)學(xué)報(bào):自然科學(xué)版，2012,39(2)：24-28.

[4] 汲曉磊.LTE-A下行信道估計(jì)技術(shù)及DSP實(shí)現(xiàn)[D].成都：電子科技大學(xué)，2013.

[5] 馬志.TD-SCDMA系統(tǒng)中基于數(shù)據(jù)域統(tǒng)計(jì)信息的MMSE信道估計(jì)算法研究[D].北京：北京郵電大學(xué),2013.

[6] Assalini A,Dall’Anese E,Pupolin S.On the robustness of MIMO LMMSE channel estimation[J].Wireless Communications,IEEE Transactions on,2010,9(11):3313-3319.

[7] 陳貝，陳發(fā)堂，石偉萍.LTE-A系統(tǒng)下行鏈路信道估計(jì)的性能評(píng)估[J].電子技術(shù)應(yīng)用，2013,39(8)：95-97.

[8] 薛毅.數(shù)值分析與實(shí)驗(yàn)[M].北京.北京工業(yè)大學(xué)出版社,2005:35-39.

[9] 張德民，孟莎莎，陳貝.LTE系統(tǒng)中基于傳輸分集的信號(hào)檢測(cè)的DSP實(shí)現(xiàn)[J].自動(dòng)化儀表，2014,35(10):75-79.

[10]田黎育，何佩琨.TMS320C6000系列DSP編程工具與指南[M].北京：清華大學(xué)出版社，2006:32-45.

Research and Implementation of the Improved Channel Estimation Algorithm in LTE-A System

The receiving end of the LTE-A system needs to dynamically estimating and tracking multipath channels for satisfying the purpose of coherent demodulation; while accurate and effective method of channel estimation can improve the data transmission rate.To reduce the complexity of the matrix inverse operation in linear minimum mean square error (LMMSE) channel estimation algorithm,the low complexity LMMSE algorithm based on Gauss-Seidel algorithm is proposed.Through comparative analysis and research on several commonly used channel estimation algorithms based on pilot signal,it is found that the low complexity LMMSE algorithm features lower bit error rate and algorithm complexity.Finally,the low complexity LMMSE algorithm based on Gauss-Seidel algorithm and the DSP implementing scheme of each sub-module are designed respectively.

Advanced long term evolution LTE-A Channel estimation Coherent demodulation Linear minimun mean square error(LMMSE) algorithm Gauss-Seidel algorithm Least square algorithm DSP

國(guó)家科技重大專項(xiàng)基金資助項(xiàng)目(編號(hào)：2011ZX03001-003-01)。

陳發(fā)堂(1965-)，男，1999年畢業(yè)于北京郵電大學(xué)應(yīng)用數(shù)學(xué)專業(yè)，獲碩士學(xué)位，研究員；主要從事TD-SCDMA移動(dòng)通信系統(tǒng)開(kāi)發(fā)及TD-LTE系統(tǒng)開(kāi)發(fā)工作。

TH89;TP336

A

10.16086/j.cnki.issn1000-0380.201601003

修改稿收到日期：2015-03-17。