乘積空間上的抽象Hardy空間

龔汝明

(廣州大學 數學與信息科學學院， 廣東 廣州 510006)

乘積空間上的抽象Hardy空間

龔汝明

(廣州大學 數學與信息科學學院， 廣東 廣州 510006)

文章首先定義抽象Hardy空間；然后給出保證算子從抽象Hardy空間到L1空間有界的一般條件;最后，定義乘積空間上的BMO空間，并研究了其與抽象Hardy空間的關系.

乘積空間; Hardy空間; BMO

0 Introduction

The development of the theory of Hardy spaces inRnwas initiated by STEIN, et al[1], and was originally tied to the theory of harmonic functions. Realvariable methods were introduced into this subject by FEFFERMAN, et al[2]; the evolution of their ideas led eventually to characterizations of Hardy spaces via the atomic or molecular decomposition. See for instance[3]and references therein.

In order to establish Calderón-Zygmund theory with multiparameter, fourier analysis on product spaces was introduced later in the ’70 s and studied extensively in the ’80 s by a number of well known mathematicians, including CHANG, FEFFERMAN, JOURNé[4-8]. For recent works, see also Refs[9-13]. In this paper, we study the Hardy spaces defined on domains inRn×Rm. Note that domains inRn×Rmmay not be homogeneous type.

LetΩbe an open set inRn×Rmwith finite measure. Denote bym(Ω) the maximal dyadic subrectangles ofΩ. Letm1(Ω) denote those dyadic subrectanglesR?Ω,R=I×Jthat are maximal in thex1direction. In other words ifS=I′×J?Ris a dyadic subrectangle ofΩ, thenI=I′. Definem2(Ω) similarly in thex2direction. For anyR=I×J?Ω, letlbe the biggest dyadic cube containingI, so thatl×J?, where={x∈Rn×Rm:Ms(χ)(x)>1/2}. Next, letSbe the biggest dyadic cube containingJ, so thatl×S?}.??lsothatl×J?.Defineγ2(R)similarly.ThenJourne′slemma, (inoneofitsforms)says,foranyδ>0,

(1)

forsomecδdependingonlyonδ,notonΩ.

LetusdenotebyQnthecollectionofalldyadiccubesinRn:

Qn={I:IisdyadiccubeinRn}

(2)

LetAn={AI}I∈Qnbe a collection ofL2-bounded linear operator, indexed by the collectionQn. We assume that these operatorsAIare uniformly bounded onL2(Rn). Similarly we can defineQmandBmby replacingnbym.

Now, we define atoms by using the collectionAnandBm.

αcan be decomposed into

(3)

whereR?Ω(say,R=IR×JRin the sum) is maximal dyadic subrectangle ofΩand there exists a functionbRsuch that

(i)αR=AIRBJRbR;

(ii) suppbR?R;

Now we are able to define our abstract Hardy spaces:

(4)

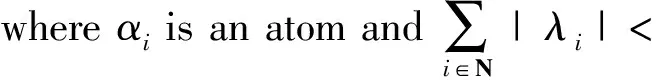
We define the norm:

(5)

1 Continuity theorem on the Hardy space

In this section, we propose some general conditions which guarantee the continuity from our Hardy space intoL1. We have the following result.

Theorem 1 LetTbe anL2(Rn×Rm)-bounded sublinear operator satisfying the following estimates: for all open setΩwith finite measure and all maximal dyadic subrectangleR=I×JofΩ, for allji≥7,i=1,2, there existsβ>nsuch that for allL2-functionsfsupported inR

(6)

(7)

(8)

(9)

(10)

In order to prove Theorem 1, we need the following result.

Lemma 1 Denote

(11)

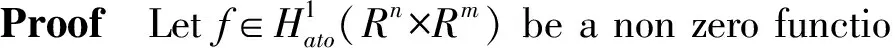
(12)

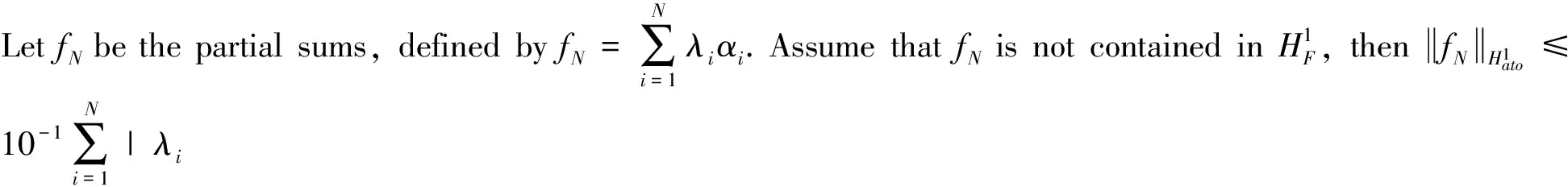
(13)

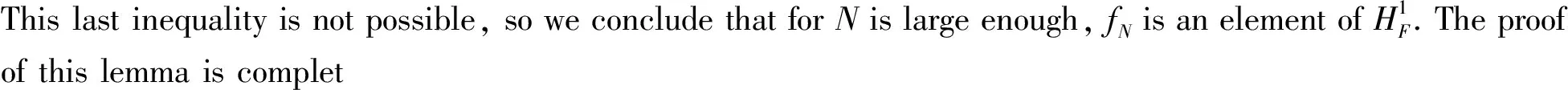
Proof of Theorem 1 From Lemma 1, we only need to prove that there exists a constantCsuch that for all atomα,

(14)

(15)

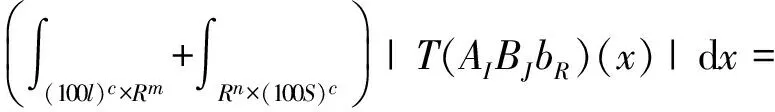
D+E.

ForthetermD,weobservethat

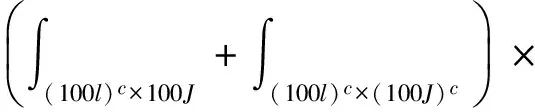
|T(AIBJbR)(x)|dx=D1+D2.

LetusfirstestimatethetermD1.UsingHolder′sinequalityandEq.(6),wehave

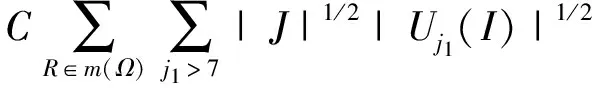
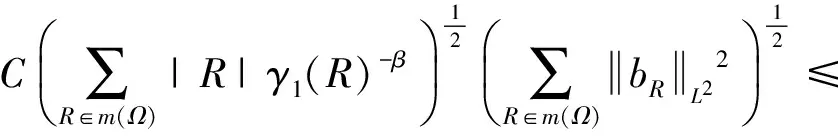
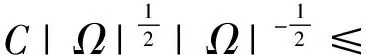
UsingHolder′sinequalityandEq.(7),wehave

|T(AIBJbR)(x)|dx≤

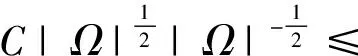
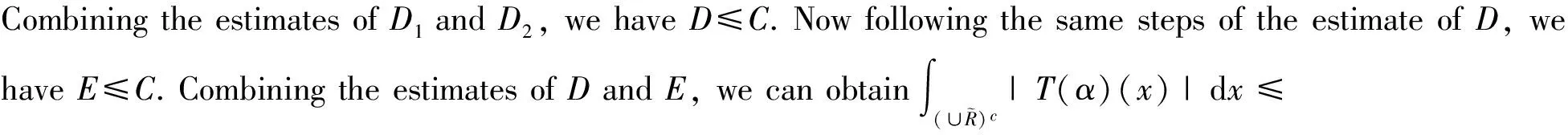
2 The dual space of Hardy space

First,wegivethedefinitionoftheBMOspace.

(16)

wherethesuptakeoverallopensetΩwith finite measure. We define BMO as the completion of Bmo with this pseudo-norm.

We have the following conclusion.

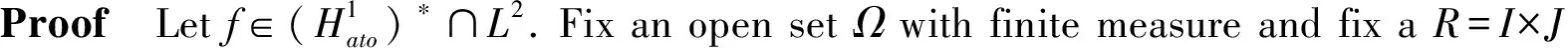
Proof Letf∈ Bmo, thenf∈L2. Letα∈L2be an atom, then there exists open setΩwith finite measure andbRsuch thatα=AIBJbR. Then we get

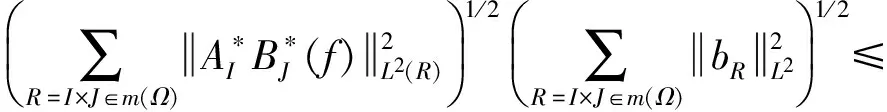
This completes the proof of this proposition.

[1] STEIN E M, WEISS G. On the theory of harmonic functions of several variables. I. The theory ofHpspaces[J]. Acta Math, 1960,103(1): 25-62.

[2] FEFFERMAN C, STEIN E M.Hpspaces of several variables[J]. Acta Math, 1972, 129(1): 137-195.

[3] HOGMANN S, LU G Z, MITREA D, et al. Hardy spaces associated to non-negative self-adjoint operators satisfying Davies-Gaffney estimates[J]. Mem Am Math Soc, 2011, 214: 78.

[4] CHANG S Y, FEFFERMAN R. A continuous version of the duality of H1 and BMO on the bidisc[J]. Ann Math, 1980, 112(1): 179-201.

[5] FEFFERMAN R, STEIN E M. Singular integrals on product spaces[J]. Adv Math, 1982, 45(2): 117-143.

[6] FEFFERMAN R. Harmonic analysis on product spaces[J]. Ann Math, 1987, 126(1): 109-130.

[7] JOURNE J L. Calderon-Zygmund operators on product space[J]. Rev Mat Iberoam, 1985, 1(3): 55-92.

[8] JOURNE J L. Two problems of Calderon-Zygmund theory on product spaces[J]. Ann Inst Fourier, 1988, 38(1): 111-132.

[9] NAGEL A, STEIN E M. On the product theory of singular integrals[J]. Rev Mat Iberoam, 2004, 20(2): 531-561.

[10]HAN Y S, LI J, LU G Z. Duality of multiparameter Hardy space Hp on product spaces of homogeneous type[J]. Ann Scuola Norm Sup Pisa, 2010, 9(4): 645-685.

[11]HAN Y S, LI J, LU G Z. Multiparameter Hardy space theory on arnot-Carath eodory spaces and product spaces of homogeneous type[J]. Trans Am Math Soc, 2013, 365(1): 319-360.

[12]LI B, BOWNIK M, YANG D C. Littlewood-Paley characterization and duality of weighted anisotropic product Hardy spaces[J]. J Funct Anal, 2014, 266(5): 2611-2661.

[13]CHEN P, DUONG X T, LI J, et al. Product Hardy spaces associated to operators with heat kernel bounds on spaces of homogeneous type[J]. Math Z, 2016, 282 (3): 1033-1065.

【責任編輯： 周 全】

Hardy spaces on product domainsGONG Ru-ming(School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China)

L1. At last, we give the definition of the BMO space and study the relationship between abstract Hardy spaces and BMO space.

product domains; Hardy spaces; BMO

O 174 Document code: A

Foundation items: Supported by NNSF of China (11301100); Specialized Research Fund for the Doctoral Program of Higher Education (20124410120002); Foundation for Distinguished Young Teachers in Higher Education of Guangdong Province (YQ2015126); Foundation for Young Innovative Talents in Higher Education of Guangdong (2014KQNCX111) and Innovation Program of Higher Education of Guangdong (2015KTSCX105).

1671- 4229(2016)06-0030-05

O 174

Received date: 2016-04-03; Revised date: 2016-06-12

Biography: GONG Ru-ming(1983- ), male, associate professor. Email: gongruming@163.com.