教學案例
——《有理數的乘法法則》
艾岱
(吉林省第二實驗學校)
教學案例
——《有理數的乘法法則》
艾岱
(吉林省第二實驗學校)
【教學目標】
知識與技能:掌握有理數的乘法法則,會用乘法法則解決兩個有理數相乘的問題。
過程與方法:通過類比小學兩個正數相乘的情形,經歷觀察、猜想、歸納總結的方法得出有理數乘法法則,在此過程中讓學生體會用已有知識解決未知問題的樂趣。
情感態度與價值觀:讓學生在知識的行程過程中感受數學的魅力,在游戲中學,體會數學帶給我們的快樂。
【教學重點】
有理數乘法法則及其運用。
【教學難點】
用含字母的一般的形式表示有理數乘法法則。
【教學過程】
一、導入
同學們去過長白山嗎?上山之前導游是不是都會建議大家租件棉服啊?因為越往上走氣溫越低。通常意義上高度每升高一千米氣溫下降6攝氏度,表示成-6℃,長白山主峰2.691千米,你將如何表示一個人從山腳登到主峰,氣溫的變化情況呢?——(-6)×2.691,這就是我們這節課所要學習的有理數乘法。
二、新課
(一)法則
師:請同學們跟老師一同回顧小學的一個加法3+3+3+3=12,為了簡化書寫我們可以把這種加數相同的加法寫成乘法4×3=12,請大家思考如果是(-3)+(-3)+(-3)+(-3)該如何寫成乘法呢?4×(-3)。我們知道(-3)+(-3)+(-3)+(-3)=-12,那么我們可以得出4×(-3)=-12,請大家結合小學的知識將下列式子寫成乘法。
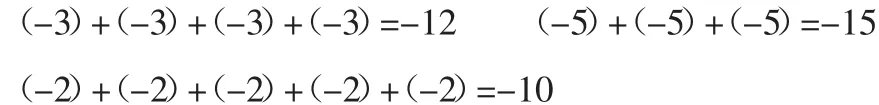
分別對應4×(-3)=-12 3×(-5)=-15 5×(-2)=-10
我們把這幾個式子與小學所學對照一下:

同學們來觀察,從第一組式子到第二組式子,等號左邊的因數發生了怎樣的變化,等號右邊的結果又發生了怎樣的變化?生:等號左邊的一個因數變成了原數的相反數,等號右邊的結果也變成了原數的相反數。師:由此請你猜想,下面一組算式的結果如何?


生:根據剛才得出的結論答案分別得12,15,10。
師:大家猜得很好,事實的確如此。下面我們分別觀察這三組算式:

你覺得他們應該分成幾類呢?生:兩類,一和三組是一類,表示同號兩數相乘;第二組是一類,表示異號兩數相乘。師:那你發現它們的結果有什么規律嗎?生:同號得正、異號得負。師:好,我們得出了有理數乘法的一條法則——兩個有理數相乘,同號得正,異號得負,并把絕對值相乘。師:有理數相乘還有其他類型嗎?生:還有零。零和任何數相乘都得零。
(二)例題
請結合法則完成以下例題:

(三)游戲
一副撲克牌,規定紅色為正、黑色為負、大小王為0,從中抽兩張做乘法,看誰算得又快又準。
(四)歸納
師:無論我們抽出多少撲克牌也無法列舉出所有有理數相乘的情形,那我們能不能用統一的形式把有理數乘法的情況概括出來呢?
我們用a代表正數,即a>0,那么

(五)練習

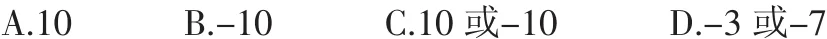
(六)小結
通過本節課的學習,我們除了掌握有理數乘法法則之外,還要會應用法則解決具體的問題。同時要體會由特殊到一般的數學思想方法。
·編輯 王團蘭

