雙層位勢問題新的基本解法公式
郭 璇,張耀明
(山東理工大學理學院,山東淄博255049)
雙層位勢問題新的基本解法公式
郭 璇,張耀明
(山東理工大學理學院,山東淄博255049)
基于單層位勢和疊加原理的傳統的基本解法,在求解某些有限域問題時,虛邊界位置的選擇會受到一定的限制,在求解某些無限域問題時可能會無解。為此提出了基于雙層位勢和疊加原理的改進的基本解法,避免了傳統基本解法的不足。該方法適合求解任何邊值問題,其特點是有限域問題和無限域問題的基本解法公式具有不同的形式。
基本解法;雙層位勢;位勢問題
基本解法(MFS)是由Kupradze和Aleksidze[1]在20世紀60年代提出的一種著名的邊界型數值方法。基本解法的優點是不需要劃分網格或者單元,也不需要邊界積分,同時避免了邊界元法中的奇異性和幾乎奇異性,具有程序設計簡單、計算速度快、計算精度高等優點,至今已被廣泛應用于各個領域,取得了很好的效果[2-8]。然而,基于單層位勢和疊加原理的傳統的基本解法具有一定的局限性,如在求解某些有限域問題時,虛邊界位置的選擇會受到一定的限制,在求解某些無限域問題時可能無解。此外,基本解法的數值解的精度與虛擬邊界的選取位置密切相關,距離太近無法避免基本解的奇異性,距離太大有時可能導致線性系統矩陣高度病態,不能求得問題的有效解。虛、實邊界之間的“距離選擇”一直是一個未能很好解決的問題,一般靠研究者的經驗和誤差實驗進行判斷。針對這些情況,文獻[9-10]分析了距離選擇與問題解的性態之間的關系,結果表明:當問題的解可以解析開拓時,虛、實邊界之間的“最大距離”不受限制。文獻[11]借鑒等價間接邊界積分方程的形式改進了基于單層位勢基本解法公式,并對基本解法線性系統矩陣進行了規則化,應用于薄體結構問題的研究,但沒有從理論上分析方法的合理性。本文從理論和數值實驗兩方面對傳統基本解法的局限性進行了分析,并在此基礎上提出了基于雙層位勢的基本解法。
1 邊值問題
本文假定Ω是R2中的一個有界域,Ωc是其開補,Γ=?Ω是它們共同的邊界。有界域Ω上的邊值問題是[9]
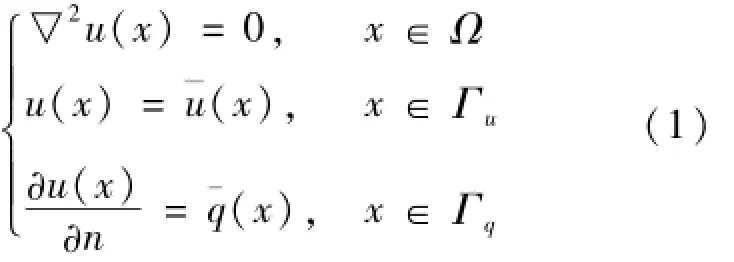
無限域Ωc上的邊值問題是
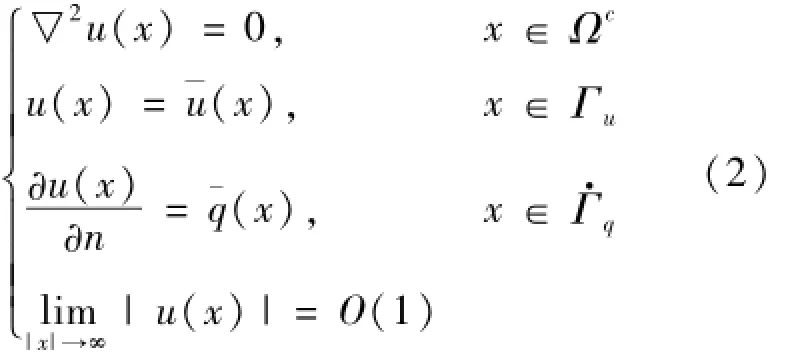
式(1)~(2)中:▽2為拉普拉斯算子;n為邊界外法線;Γu,Γq分別是u和?u/?n已知的邊界。二維位勢問題控制方程的基本解為
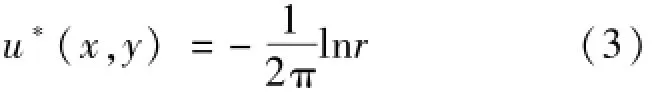
式中x=(x1,x2),y=(y1,y2)分別為場點和源點,為兩點之間的距離。
2 傳統的基本解法的局限性
傳統基本解法的公式是
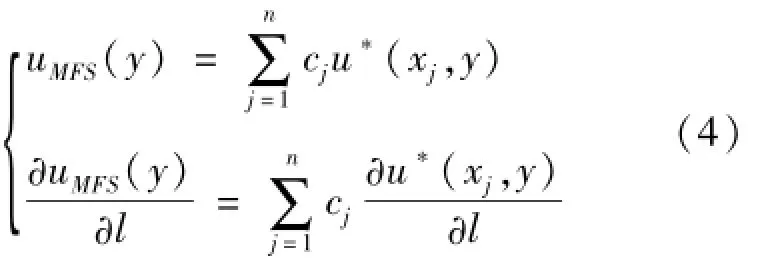
這里l=l(y)是在點y處的任一方向。
筆者發現:傳統的基本解法式(4)不具有普遍適用性。對某些內邊值問題,虛邊界(虛源位置)的選擇受到一定的限制,對于某些外邊值問題,基本解法失效。
考慮一個內邊值問題:
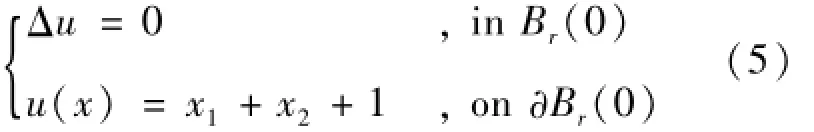
這里Br(0)是以坐標原點為中心、半徑為r<1的圓域,?Br(0)是Br(0)的邊界。顯然問題(5)的解析解是u(x)=x1+x2+1,于是u(0)=1。現在用基本解式(4)求解問題(5)。假設所選的虛源節點xj(j=1,…,n)位于單位圓周?B1上,那么對于基本解法式(4),無論{aj}取何值,總有uMFS(0)=0,因此對于任意的r<1,相應的邊值問題(5)的解總不能由基本解式(4)求得,表明虛邊界的選擇受到一定的限制。
數值結果也表明了這一點。在應用傳統基本解式(4)求解問題(5)時,取r=1/2,選擇44個均布的虛源點位于單位圓周上。表1給出了部分邊界節點上邊界通量?u/?n的數值結果,表2給出了內點溫度的數值結果。從表1和表2可看出:無論是內點計算,還是邊界點計算,結果都不正確,驗證了前面的理論分析。
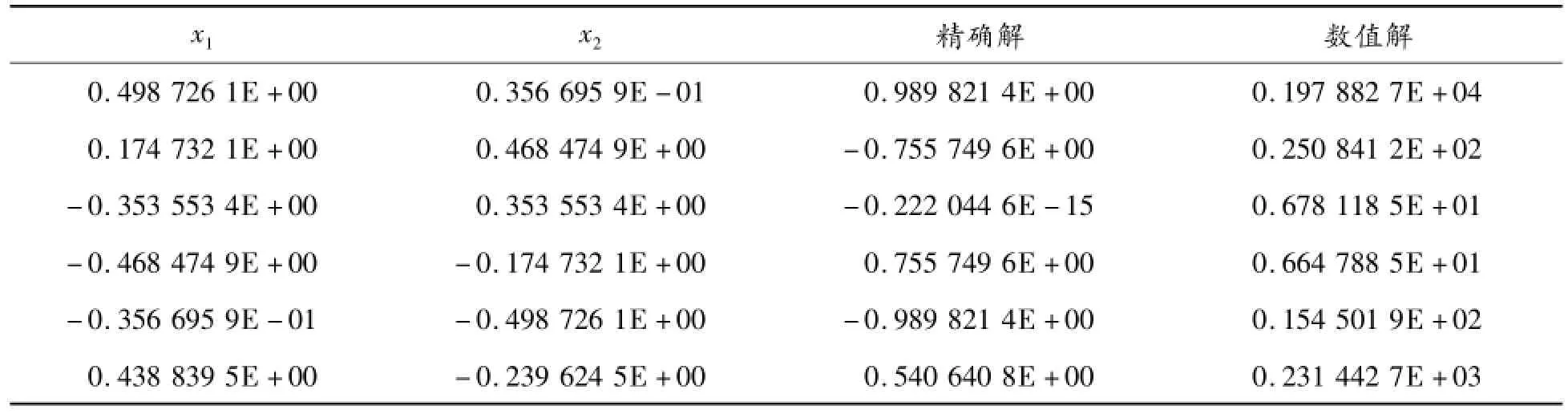
表1 邊界法向通量的數值結果
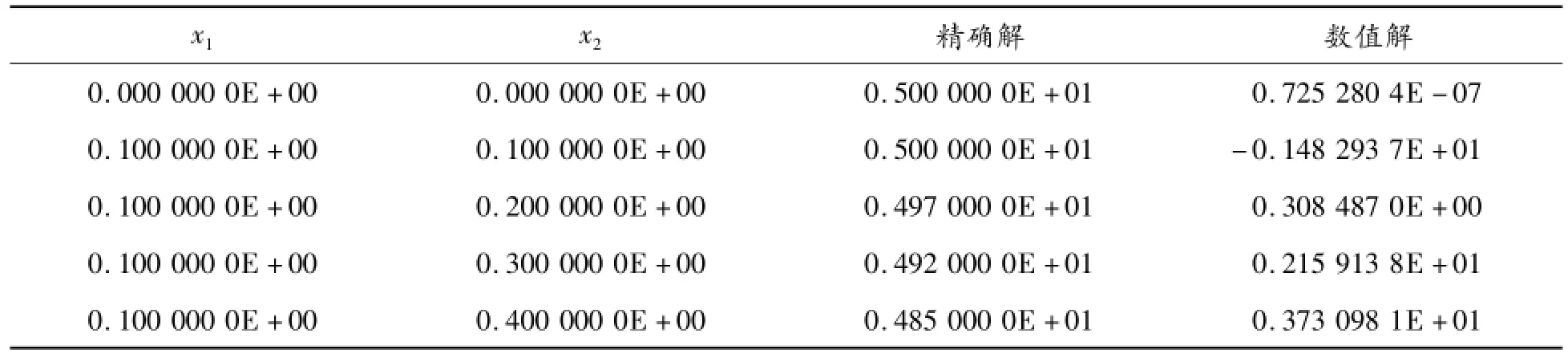
表2 內點溫度的數值結果
現在考慮如下外邊值問題
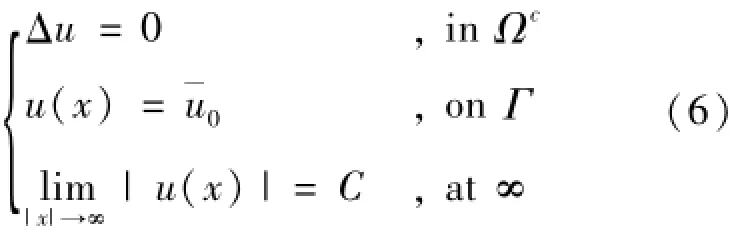
例如,考慮如下邊值問題
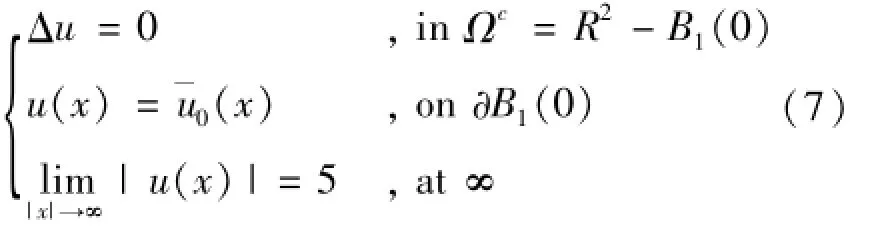
這里B1(0)是中心在原點、半徑為1的圓域,是其邊界
在應用傳統基本解式(4)求解問題(7)時,44個虛源點均布在半徑為0.5的圓周上。表3給出了部分邊界節點上邊界通量?u/?n的數值結果,表4給出了內點溫度的數值結果。從表3和表4可看出:內點和邊界點的數值結果都不正確,驗證了前面的理論分析。
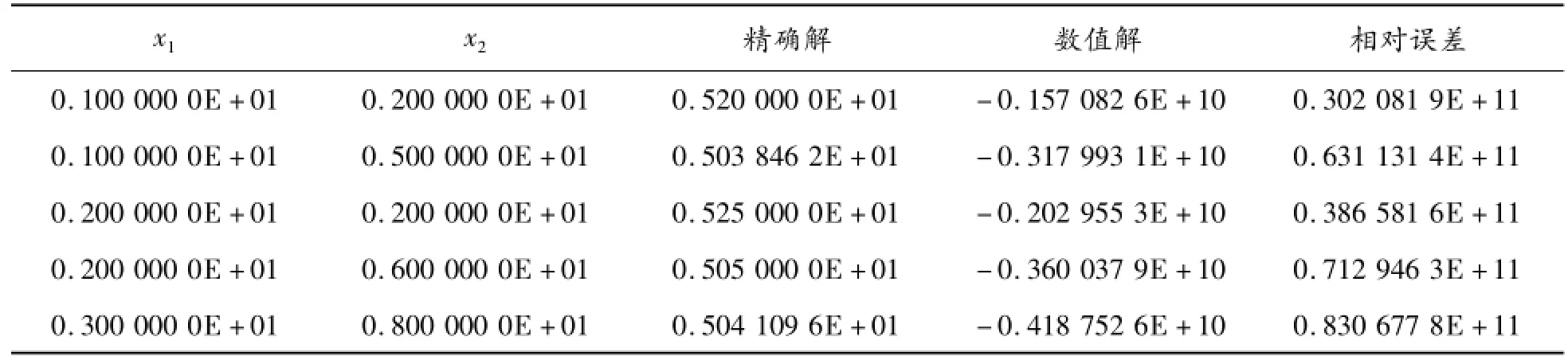
表3 內點溫度的數值結果
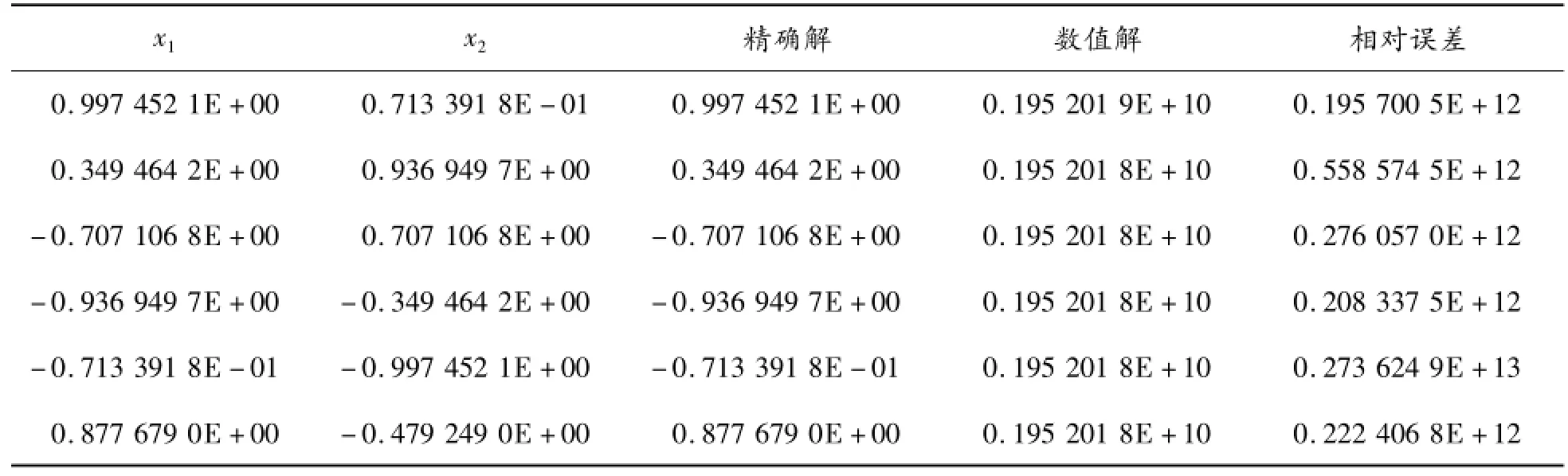
表4 邊界法向通量的數值結果
3 基于雙層位勢的基本解法
為了避免傳統基本解法的不足,本文提出基于雙層位勢的基本解法。對于內邊值問題(1),基本解法公式是
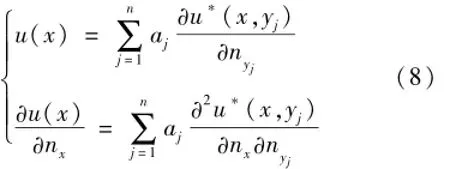
現在應用基于雙層位勢的基本解法式(8)求解問題(5),仍取r=1/2。同樣地,選擇44個虛源點均布于單位圓周?B1(0)上。表5給出了內點溫度的數值結果,表6給出了部分邊界點上的法向通量?u/?n的數值結果。從表5和表6可以看出:無論是內點溫度的數值結果還是邊界量的數值結果都達到了很高的精度。這表明:基本解式(8)完全避免了傳統的基本解式(4)的弊病。
對于外邊值問題(2),基于雙層位勢的基本解法公式是
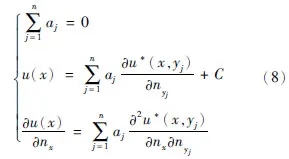
現在應用基本解法式(8)來求解問題(3)。同樣地,選擇44個虛源點均布于半徑為0.5的圓周上。表7給出了內點溫度的數值結果,表8給出了部分邊界點上的法向通量?u/?n的數值結果。從表7和表8可以看出:無論是內點溫度的數值結果還是邊界量的數值結果都達到了很高的精度。這表明:基本解式(8)完全地避免了傳統的基本解式(4)的弊病。
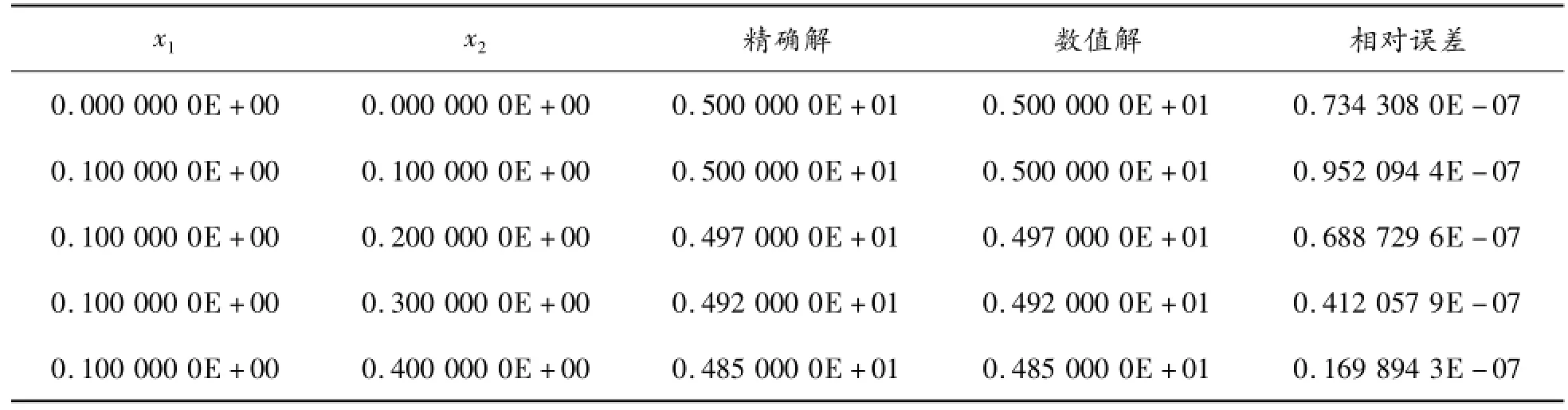
表5 內點溫度的數值結果
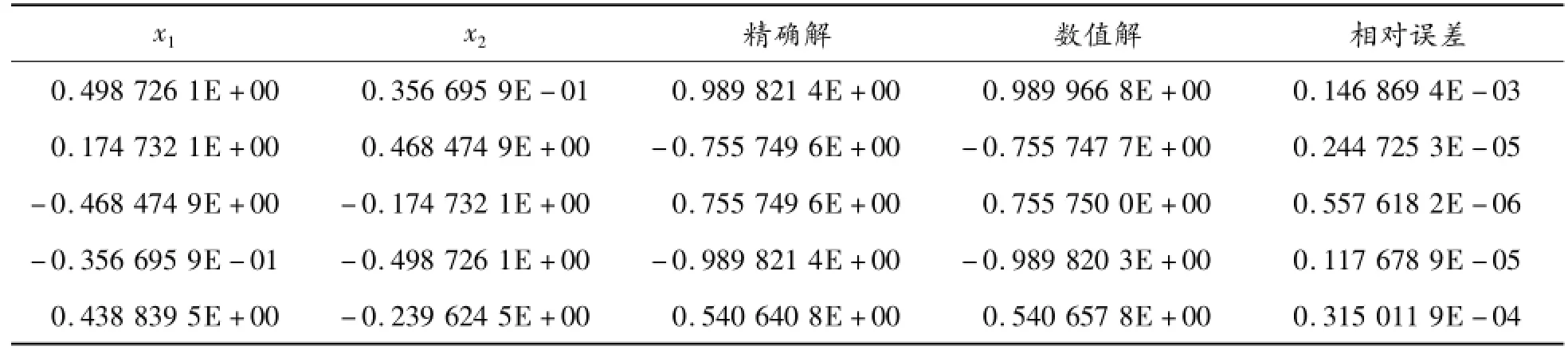
表6 邊界法向通量的數值結果
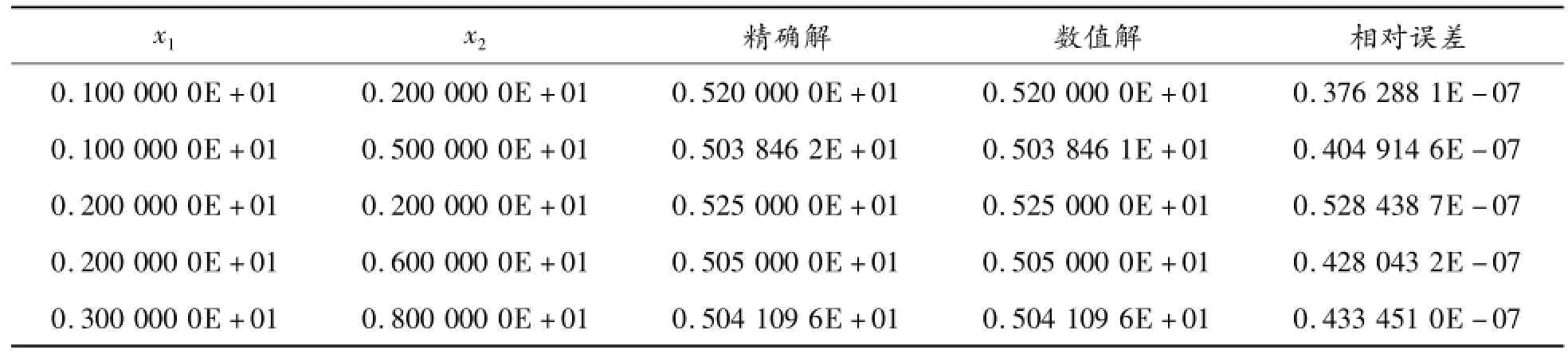
表7 內點溫度的數值結果
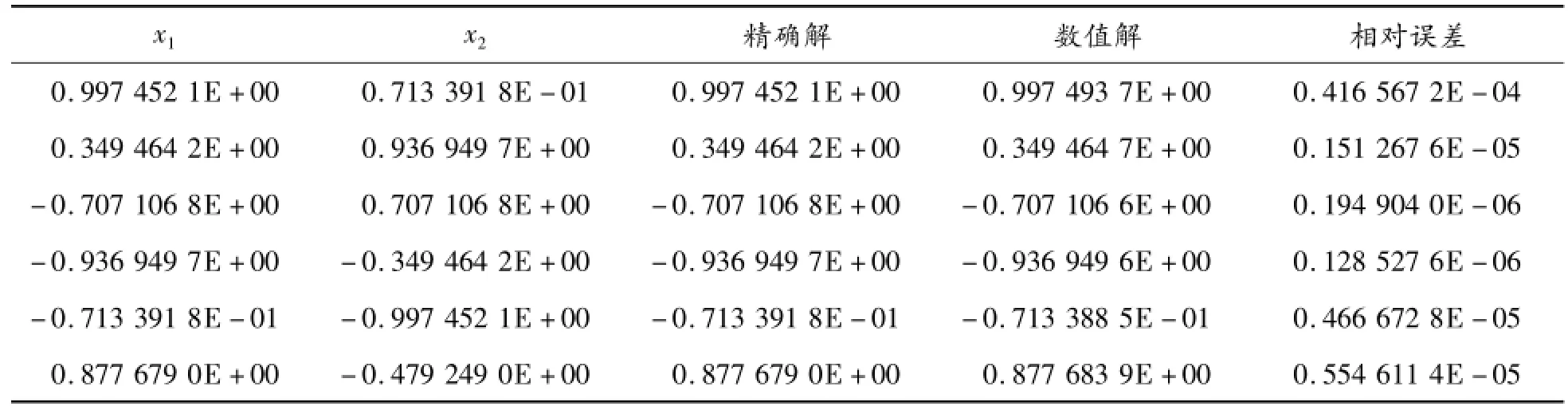
表8 邊界法向通量的數值結果
4 結束語
傳統的基本解法基于單層位勢和疊加原理,具有一定局限性。本文從理論和數值計算兩方面進行了分析,提出了基于雙層位勢和疊加原理的基本解法,可適合于求解任何邊值問題。
[1] KUPRADZE V D,ALEKSIDZE M A.The method of functiona1 equations for the approximate solution of certain boundary value prob1ems[J].USSR Comput.Math.Math.Phys,1964(4):82-126.
[2] FAIRWEATHERG,KARAGEORGHISA.The method of fundamenal solutions for elliptic boundary value problems[J].Adv Comput Math 1998(9):69-95.
[3] POULLIKKASA,KARAGEORGHIS A,Georgiou G.Methods of fundamental solutions for harmonic and biharmonic boundary value problems[J].Comput.Mech,1998,21:416-423.
[4] GOLBERGM A,CHEN CS.The method of fundamental solutions for potential,Helmholtz and diffusion problems.Boundary integral methods:numerical and mathematical aspects[M].Boston:WIT Press and Computational Mechanics Publications,1999.
[5] KITAGAWA T.On the numerical stability of the method of fundamental solution applied to the Dirichlet problem[J].Jpn JAppl Math,1988(5):123-133.
[6] GEORGE S A F,YOUSSEF F R.The method of fundamental solutions applied to3D elasticity problems using a continuous collocation scheme[J].Engineering Analysis with boundary elements,2009,33:330-341.
[7] BOSELLIF D,OBRIST L,KLEISER.A multilayer method of fundamental solutions for Stokes flow problems[J].Journal of Computational Physics,2012,231:6139-6158.
[8] GUIMARAES S,TELLES JC F.The method of fundamental solutions for fracture mechanics-Reissner’s plate application[J].Engineering Analysis with boundary elements,2009,33:1152-1160.
[9] 孫煥純.無奇異邊界元法[M].大連:大連理工大學出版社,1999.
[10]張耀明,孫煥純,楊家新.虛邊界元法的理論分析[J].計算力學學報,2000,17(1):56-62.
[11]王發杰,張耀明,公顏鵬.改進的基本解法在薄體各向異性位勢Cauchy問題中的應用[J].工程力學,2016,32(2):18-24.
(責任編輯陳 艷)
A New Method of Fundamental Solution Formulation to Double Layer Potential Problems
GUO Xuan,ZHANG Yao-ming
(School of Mathematics,Shandong University of Technology,Zibo 255049,China)
The conventional method of fundamental solution(MFS),based on the single layer potential and the superposition principle,has many shortcomings,for instance,for special interior problems its fictitious boundary location may be limited and for certain exterior problems it may fail.In this paper,a new method of fundamental solution formulation,which is built on the double layer potential and the superposition principle,is developed.The method avoids some disadvantages of the traditional method of fundamental solution and thus is suitable for solving any boundary value problems.
method of fundamental solution(MFS);double layer potential;potential problems
O241.8
A
1674-8425(2016)12-0165-06
10.3969/j.issn.1674-8425(z).2016.12.026
2016-05-27
山東省自然科學基金重點資助項目(ZR2010AZ003)
郭璇(1992—),女,碩士研究生,主要從事科學計算與力學研究,E-mail:m18369972890@163.com。
郭璇,張耀明.雙層位勢問題新的基本解法公式[J].重慶理工大學學報(自然科學),2016(12):165-170.< class="emphasis_bold">Citationformat:
format:GUO Xuan,ZHANG Yao-ming.A New Method of Fundamental Solution Formulation to Double Layer Potential Problems[J].Journal of Chongqing University of Technology(Natural Science),2016(12):165-170.

