具有脈沖時滯和Holling Ⅲ型的捕食者食餌系統正周期解的存在性

葉麗霞，張 忠

（1.武夷學院數學與計算機學院，福建武夷山354300；2.重慶大學數學與統計學院，重慶400030）

具有脈沖時滯和Holling Ⅲ型的捕食者食餌系統正周期解的存在性

葉麗霞1，張 忠2

（1.武夷學院數學與計算機學院，福建武夷山354300；2.重慶大學數學與統計學院，重慶400030）

利用重合度理論及Mawhin連續性定理，研究了一類具有脈沖時滯和HollingⅢ類功能反應的捕食者食餌系統正周期解的存在性問題，得到系統存在正周期解的充分條件，并推廣和改進部分已有結果。

脈沖效應；時滯；Holling Ⅲ型功能反應；重合度；正周期解

近年來，具有Holling功能反應的生態系統模型及其變形引起了廣泛的關注。許多學者利用不同的方法研究了不同類型功能反應的捕食者-食餌系統的周期解的存在性［1－5］。另外，生態系統是漸變的系統，無法避免外界突發干擾，因而廣泛存在時滯現象和脈沖效應，如環境突變，山洪、地震的爆發，其他物種的遷入和人為添加種群幼崽，幼兒捕食者與成年捕食者捕食能力的不同等會導致種群數量許多出現瞬時變化，即表現為脈沖效應。具有時滯和脈沖效應的生態系統模型引起許多學者的關注，得到許多相關研究成果［6－11］。本文結合脈沖效應和時滯因素及Holling Ⅲ型功能反應，利用用重合度理論及微分方程中的積分方法，得到了系統存在正周期解的一個充分條件。

本文考慮食餌種群服從Logistic增長、具有脈沖時滯和Holling Ⅲ型功能反應的捕食系統：

其中：n∈Z＋，0＜m（t）＜1；x（t），y（t）分別表示食餌、捕食者種群密度；cn，dn分別表示食餌、捕食者在t＝tn的脈沖增長率；其他參數的生態學含義參考文獻［2－4］。本文總是假設：

（A1）脈沖時刻｛tn｝，n∈Z＋滿足0＝t0＜t1＜…＜tn＜…；

（A2）存在正數ω＞0和正整數p，使得

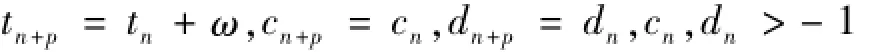
（A3）函數a，d：R R；b，c，k，τ：R R＋是連續ω－周期的，且假設系統（1）的系數都是嚴格正的ω周期函數。

設X，Z是賦范向量空間，Ω為X的有界開集，L：DomL?X→Z為線性映射，N：X→Z為連續映射，如果dim KerL＝Co dim lm L＜＋∞，且lm L為Z中閉子集，則映射L稱為指標為零的Fredholm映射。如果L是指標為零的Fredholm映射，且存在連續投影：

則L｜DomL∩KerL（I－P）X→lm L可逆，設其逆映射為Kp。如果QN（ˉΩ）有界且KP（I－Q）N：ˉΩ→X是緊的，則稱N在ˉΩ上是L－緊的。由于lm Q與KerL同構，因而存在同構映射J：lm Q→KerL。

以下給出相關引理：

引理1（Mawhin連續性定理）［10］記Ω?X是一有界開集，L：Dom L?X→Y是一個指標為零的Fredholm算子，N：X→Z為ˉΩ上的L－緊的，假設

1）對任意λ∈（0，1），Lx→λNx的任意解滿足x??Ω；

2）對任意x∈?Ω∩KerL，QNx≠0且deg｛JQN，Ω∩KerL｝≠0。

那么算子方程Lx＝Nx在DomL∩ˉΩ至少有一個解。

引理2 在引理1條件1）和2）下，R2＋是系統（1）的不變集。

為方便，設J?R，記PC＝｛g：J→R2｜g（t）在t≠tk處連續，在t＝tk處左連續，右極限存在｝。對ω－周期函數g（t）和ω－周期序列｛cn｝，｛dn｝，本文采用以下記號：

利用上面的引理和記號，討論系統（1）的周期解的存在性。

則系統（1）至少存在一個ω－正周期解。

證明 作變換x（t）＝exp｛u（t）｝，y（t）＝exp｛v（t）｝，則系統（1）等價于：

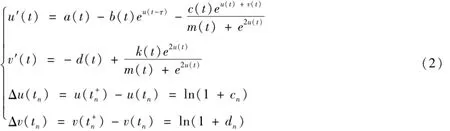
設：

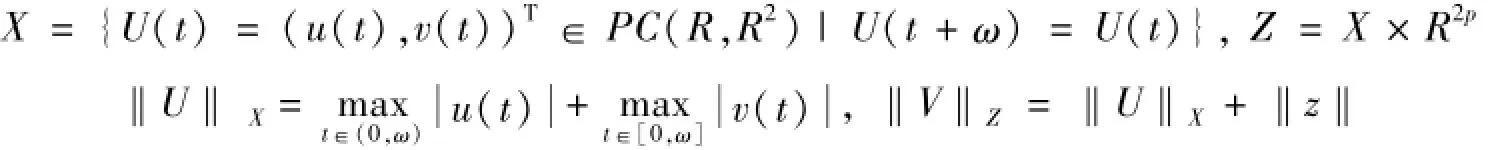
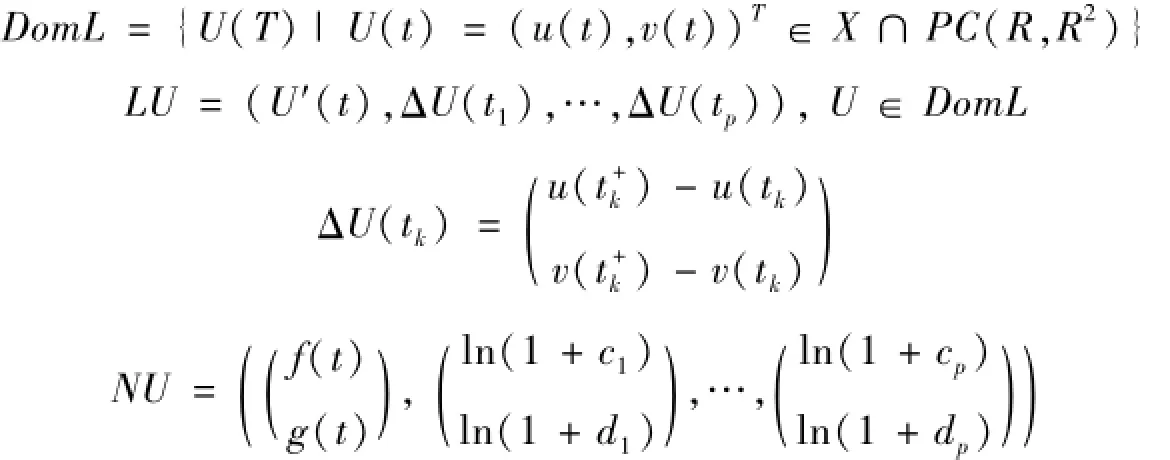
其中：

則

因此，dim KerL＝Co dim lm L＜＋∞且lm L在Z中是閉的，即L是一個指標為零的Fredholm算子。對于U∈ X，V＝（U，z1，…，zp）∈Z，定義連續投影算子P：X→X和Q：Z→Z為

則lm P＝KerL，lm L＝KerQ＝lm（I－Q），而且L｜DomL∩KerP：（I－P）X→lm L存在逆映射，記為KP：lm L→ DomL∩KerP。對任意的V＝（U，z1，…，zp）∈Z，必存在χ∈X，使得

由此可知QN與Kp（I－Q）N是連續的。再根據Arzela-Ascoli定理，對?Ω?X有界開集，易證緊算子。

接下來估計使得引理1的2個條件成立的有界開集Ω。不妨設Ω＝｛U｜‖U‖＜H｝，其中H為待定的常數。

對?λ∈（0，1），由算子方程LU＝λNU，U∈X有

式（2）從0到ω積分得：

由式（2）和（4）有

從而根據式（2）和（5）有

由于（u，v）T∈X，則存在ξi，ηi∈［0，ω］，i＝1，2，使得

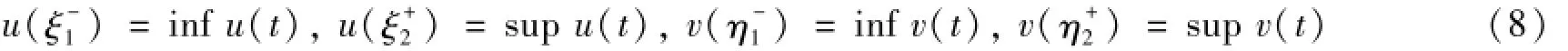
由式（5）和（8）知

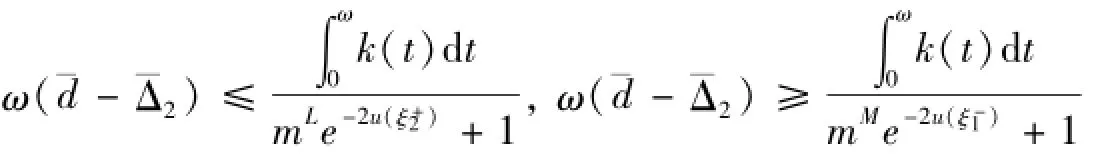
即

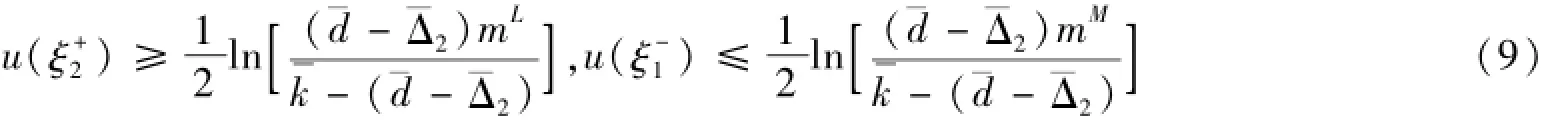
所以：

又由于

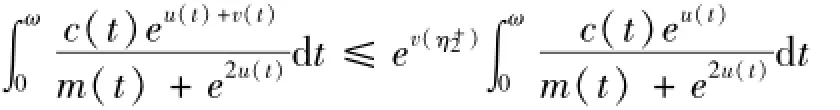
且由式（4）和（10）可得

因此有

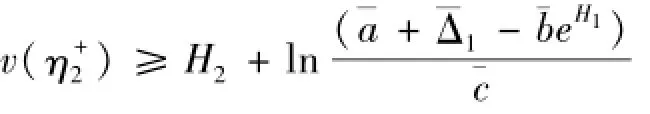
又由于

且由式（4）、（10）和（11）可得

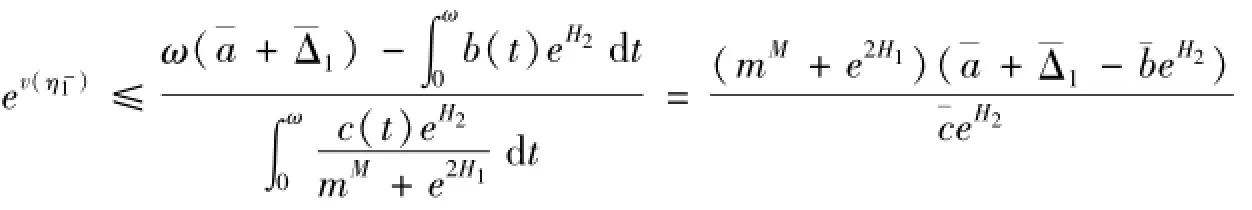
則有

所以：

至此，對任意的λ∈（0，1），已對算子方程LU＝λNU的解u（t），v（t）作了估計，這里與λ無關。取其中H為充分大的數，使由上面估計可知，任意λ∈（0，1），LU＝λNU的任意解滿足x??Ω，即引理1的第一個條件成立。為了驗證第2個條件，考慮關于（u，v）T∈R2的代數方程組：

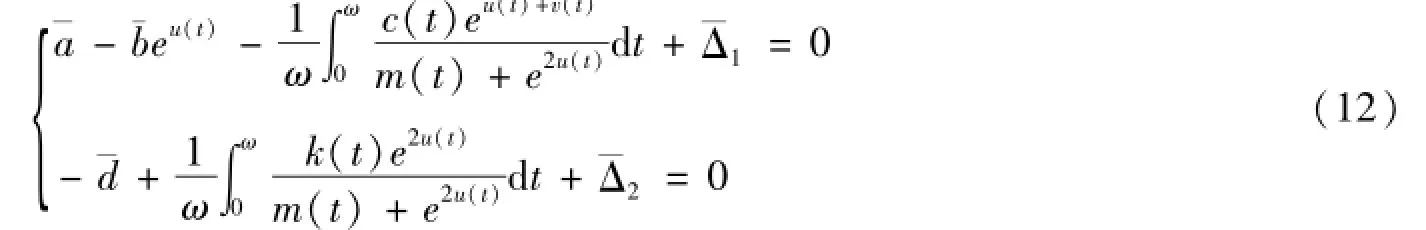
其中μ∈［0，1］。類似上面的估計過程。容易證明對于?μ∈［0，1］，方程（12）的解（u，v）T有界，實際上，它也滿足估計：

對于任意U∈?Ω∩KerL，因U＝（u，v）T是R2中滿足‖U‖＝H的常數，則有

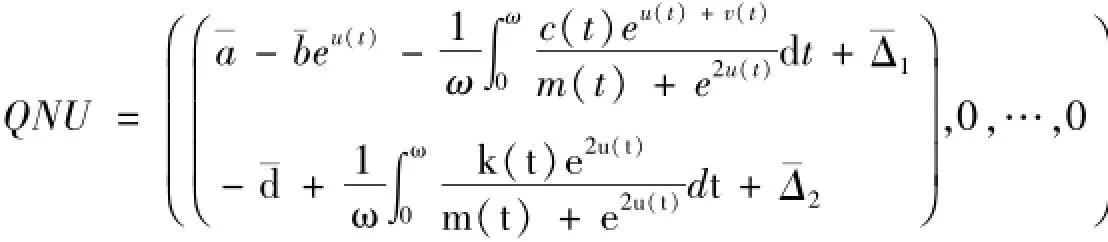
由式（9）得，對任意的U∈?Ω∩KerL，都有QNU≠0。為了計算Brouwer度，構造同構變換G（μ，U）＝μQNU＋（1－μ）H（U），μ∈［0，1］，這里U＝（u，v）T且

從式（12）可以看出：對任意U∈?Ω∩KerL和μ∈［0，1］，都有G（μ，U）≠0。由假設得H（U）＝0都有唯一解。由lm Q＝KerL，取J＝I，并利用同構不變的性質得deg｛JQN，Ω∩KerL，0｝＝deg｛QN，Ω∩KerL，0｝＝deg｛N，Ω∩KerL，0｝≠0。因此，驗證了引理1的所有條件，從而LU＝NU在DomL∩ˉΩ上至少有1個解（U*（t），V*（t））T，且也是方程（1）的周期解。所以（x*（t），y*（t））T＝（exp｛u*（t）｝，exp｛v*（t）｝）T也是方程（1）的正周期解。證明完畢。

［1］ 范猛，王克.一類具有HollingII型功能性反應的捕食食餌系統全局周期解的存在性［J］.數學物理學報，2001，21A（4）：492－497.

［2］ 葉丹，范猛，張偉鵬.一類具有HollingII型功能性反應的捕食食餌系統非平凡周期解的存在性［J］.工程數學學報，2004，21（4）：504－508.

［3］ 任磊.一類具有HollingII型功能性反應的捕食食餌系統正周期解的存在性［J］.魯東大學學報，2008，24（3）：199－202.

［4］ 唐小平，李靖云，高文杰.食餌被開發并具有Holling Ⅲ型的捕食系統周期解的存在性［J］.四川師范大學學報（自然科學版），2008，31（2）：1001－8395.

［5］ 劉振杰，范鷹，于景偉.具有稀疏效應和Holling Ⅲ類功能性反應的捕食者食餌模型周期解［J］.哈爾濱工業大學學報，2007，12（2）：63－65.

［6］ 譚遠順，徐曉曼，夏江.一類食餌具時滯與擴散的非線性脈沖捕食系統正周期解存在性［J］.生物數學學報，2012，27（2）：333341.

［7］ 楊志春.具有時變時滯和Holling-N類功能反應的脈沖捕食系統的周期解［J］.數學的實踐與認識，38（16）：85－91.

［8］ 徐炳祥，曾志軍.一類具有Holling Ⅲ型功能性反應的捕食者食餌系統的周期解的存在性［J］.純粹數學與應用數學，2012，28（4）：1008－5513.

［9］ 施秀蓮.一類具有Holling Ⅲ型功能性反應的捕食者食餌系統的周期解的存在性與穩定性［J］.應用數學學報，2011，34（2）：272－282.

［10］鐘秀敏，劉秀湘.脈沖時滯Hassell-Varley-Holling型功能性反應的捕食者食餌系統的周期解存在的充要條件［J］.應用數學學報，2012，35（2）：297－308.

［11］SHIHong-bo.permanence and periodic solutions of a delayed predator-prey system with impulse［J］.ApplMath，2010，25（3）：264－276.

（責任編輯劉 舸）

Existence of Periodic Solutions Holling Ⅲ Prey-Predator System w ith Tim e-Varying Delay

YE Li-xia1，ZHANG Zhong2

（1.Department of Mathematics and Computer，Wuyi University，Wuyishan 354300，China；2.Department of Mathematics and Statistics，Chongqing University，Chongqing 400030，China）

：By utilizing Mawhin’s coindidence degree theory and Mawhin’s Continuity theorem，a criterion for the periodic solution of the Holling Ⅲ predator-prey systems with time-varying delay is further investigated.The criterion improves several recent works.The sufficient conditions for the existence of positive periodic solution of the system is presented.

time-varying delay；HollingⅢfunctional response；coindidence degree theory；periodic solution

O175

A

1674－8425（2016）12－0171－06

10.3969／j.issn.1674－8425（z）.2016.12.027

2016－10－06

國家自然科學基金資助項目11202249）；福建省校科研基金資助項目（XL201508）

葉麗霞（1987—），女，碩士，主要從事生物數學研究，E-mail：yelixia2015＠126.com。

葉麗霞，張忠.具有脈沖時滯和Holling Ⅲ型的捕食者食餌系統正周期解的存在性［J］.重慶理工大學學報（自然科學），2016（12）：171－176.

format：YE Li-xia，ZHANG Zhong.Existence of Periodic Solutions Holling Ⅲ Prey-Predator System with Time-Varying Delay［J］.Journal of Chongqing University of Technology（Natural Science），2016（12）：171－176.